基于队列理论CSMA/CA机制的无线传感器异构机制OSTS的实时性分析
吕春峰,朱建平
(上海交通大学 电子信息与电气工程学院,上海 200240)
随着无线通信、集成电路、传感器以及微机电系统(MEMS)等技术的飞速发展和日益成熟,低成本、低功耗、多功能的微型传感器的大量生产成为可能。这些传感器在微小体积内通常集成了信息采集、数据处理和无线通信等多种功能。无线传感器网络(WSN)就是由部署在监测区域内大量的微型传感器节点通过无线电通信形成的一个多跳的自组织网络系统,其目的是协作的感知、采集和处理网络覆盖区域里被监测对象的信息,并发送给观察者。由于微型传感器的体积小、重量轻,有的甚至可以像灰尘一样在空气中浮动,因此,人们又称无线传感器网络为“智能尘埃”,将它散布于四周以实物感知物理世界的变化。异构性[1]是无线传感器网络一个非常重要的特征,众多因素决定了异构性是无线传感器网络内在、泛在的特征。文中根据火场监控应用的实时性需要,针对传输火场环境下的温度及湿度这两个异构数据包到sink节点的无线传感器异构网络,基于队列理论分析其网络传输的实时性特征,提出了一种新的CSMA/CA机制OSTS(一次获得信道,只传一个数据包机制),以此分析及提高系统监控性能。
1 建立模型
随着IEEE802.15.4标准[2]的发布,无线传感器的应用取得突飞猛进的发展,其应用早已经由军事国防领域扩展到环境监测、交通管理、医疗健康、工商服务、反恐抗灾等诸多领域,使人们在任何时间、任何地点和任何环境条件下都能够获取大量翔实可靠的信息,最终成为一种“无处不在”的传感技术。无线传感器网络的性能优势使得其应用几乎涉及到我们生活的方方面面;但是无线传感器网络依然在很多方面存在缺陷,诸如使用电池供电引起节能的需求,公平性、实时性、吞吐量的有待提高等等。
针对于实际应用,提出了异构网络的实时性要求,详细、综合分析两种不同性质的数据包以公平的机会访问信道的时间性能,找到合适参数以减少数据包访问时间、提高实时性要求。
在提出OSTS机制,建立分析模型之前,先作出如下的假设:假设信标指数为4,所以每个包都能在同一个超帧传送完[3];数据包的接受确认可以无需通过ACK[4-5]来执行;为了避免成功获取信道的节点永久占用信道,参与竞争的所有节点而不仅仅是传送节点将其backoff计数器降为最小值;传完一个数据包后,信道为空的概率μ0与任何时刻信道为空的概率P0不相等;系统中存在2种节点,节点个数分别为N1和N2,到达节点的流量满足泊松(Poisson)过程且数据包到达率分别为λ1和λ2;参与竞争的数据包都是每个队列的首数据包,那么可以简化竞争机制,即只考虑参与竞争的数据包。这样,采用3个马尔可夫链模型来描述,其中两个半马尔可夫链分别表示两种数据包访问信道的过程,如图1所示,这个链是[5]的改进;一个宏观马尔可夫链表示信道的状态,如图2所示。
首先,考虑OSTS机制的节点访问信道的马尔可夫过程。每次参与竞争的数据包,无论是哪种类型的节点包都有公平的机会访问信道,所以只需要考虑任意一种类型的数据包访问信道的过程,而图1的实线过程表示一种节点的实际访问过程,虚线过程表示另一种数据包也在同时参与访问信道,但是并不是真正传送,仅描述它们的一种并行的公平的竞争关系。定义 S(t)(S∈(0,…,m)),C(t)(C∈(-2,…,Wi-1)),r(t)(r∈(0, …,r)) 分别为在时刻的 backoff阶段计数器大小,backoff计数器大小,重传计数器大小。任何一个节点获得信道之后,就开始传送其队列中的首包,传送该包完成后重新参与其他的节点的竞争信道的过程,即一次获得信道,只传一个数据包机制(One Service a Time Scheme)。
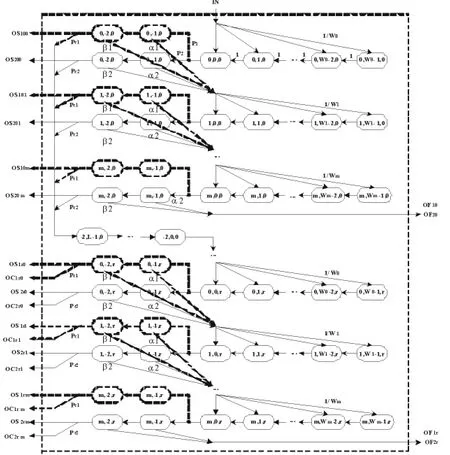
图1 时隙化的IEEE 802.15.4 CSMA/CA机制的马尔可夫链模型Fig.1 Markov chain model for slotted IEEE 802.15.4 CSMA/CA scheme
根据图1马尔可夫链的链式规则,可以得到关于各个状态间的关系式(1)~(4)。 其中式(1)表示节点获得了新包,随机选择backoff计数器后进行退避过程的转移概率;式(2)表示节点不论信道的状态,都以概率1递减其backoff计数器的转移概率;式(3)表示节点在任意一个CCA发现信道忙后进入下一个backoff阶段的转移概率;式(4)表示达到最大backoff阶段后节点选择下一次重传的转移概率。
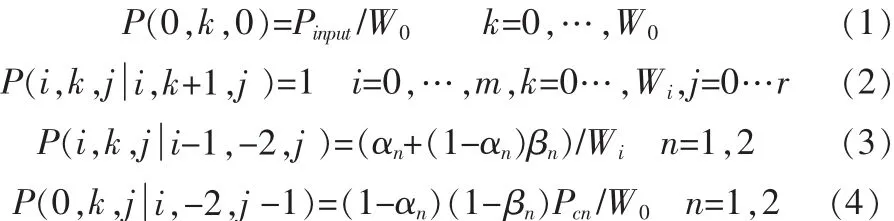
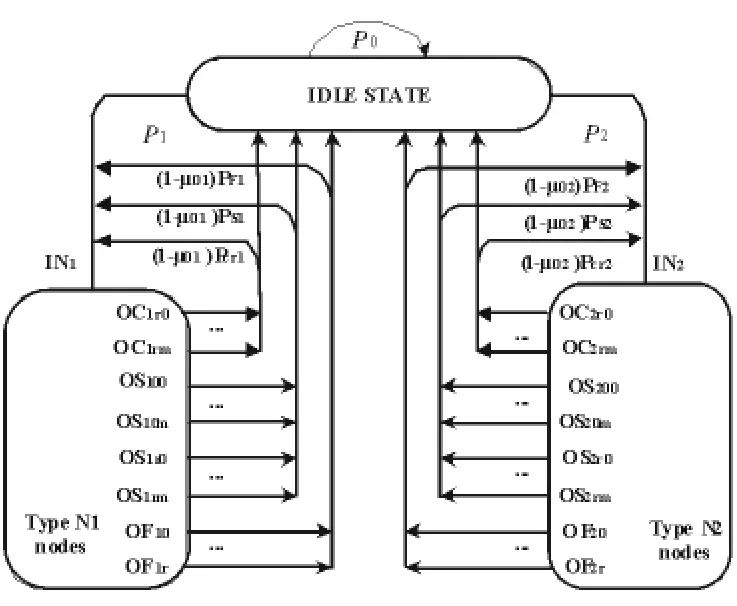
图2 宏观马尔可夫链Fig.2 Macroscopic states transition for two types of nodes
其次,从信道的状态来看,两种数据包的访问信道的状态转移情况可以直观地从图2中宏观马尔可夫链看出,并且得到式(5)~(11)。 其中式(5)~(7)分别表示任何一种节点在访问失败、最后一次重传的冲突传送、每次重传的成功传送,若缓存中没有其他数据包,那么直接转移到idle状态的转移概率;式(8)表示任何一个节点都没有新数据包,处于idle状态的概率;式(9)~(11)分别表示任何一种节点在访问失败、最后一次重传的冲突传送、每次重传的成功传送,若缓存中还有其他数据包,那么重新转移到竞争传送状态的转移概率。
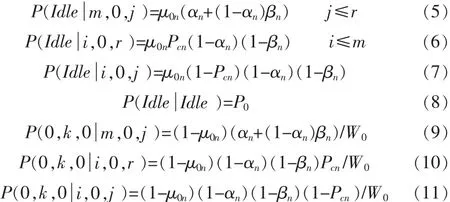
定义 bi,k,j=P{s(t),c(t),r(t)=i,k,j}为马尔可夫链的稳态转移概率,那么根据马尔可夫链和其状态转移的规则,可以得到式(12)。通过归一化处理,得到式(13)。式13中每个量分别为表达式(14)和(15)。式(14)表示一种类型的包在访问信道时backoff过程稳态概率、CCA1概率、CCA2概率、成功传送概率、冲突传送概率。式(15)表示空闲概率,其中P0表示任何时刻信道为空的概率,μ0表示传完一个数据包后,信道为空的概率。

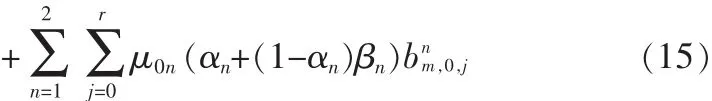
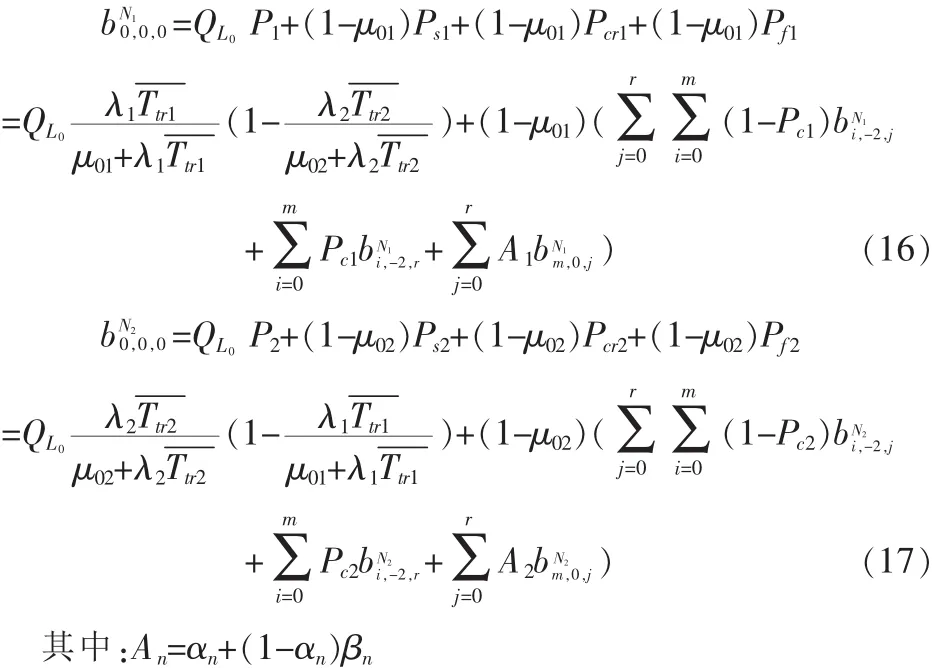
从上面的分析中,看到这些概率实际上都是与信道的操作点α,β,τn有关,且这些操作点参数决定了数据包的访问时间度量,其中α表示节点在CCA1后发现信道忙的概率;β表示节点在CCA2都发现信道忙的概率;τn表示节点侦听信道的概率。第二部分会详细分析这个操作点以获取访问时间性能分析。
2 延时性能分析
在低速率传输的WSN中,除了能耗是个重要的参数,实时性也是一个非常重要的参数,特别是对于这样的实时性要求比较高的应用环境。访问时间度量(delay)是指从数据包到达MAC队列的时刻到数据包成功传送的时刻之间的时间。假设理想信道,那么数据包的失败率只是因为数据包之间的冲突。因每次竞争都是节点队列中的首包,那么简单的从数据包访问情况来获得信道的操作点,其中τn就是所有backoff计数器降为0的概率。
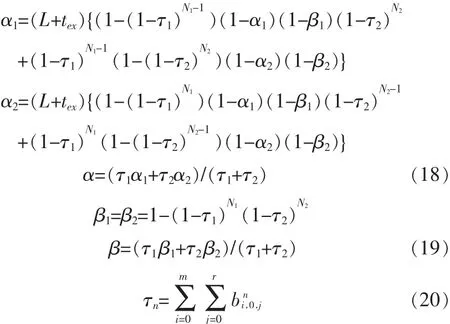
从上面的式(18)~(20)可以看到操作点参数可以通过数学迭代的方法唯一求出,从而可以得到数据包的传输时间度量。引入M/G/1/K队列理论分析节点中的数据包的传送情况。队列有K个数据包,每个数据包的长度为L,每个数据包的传送时间的概率母函数为 Ttr(Z)[6],那么 P0和 μ0为:
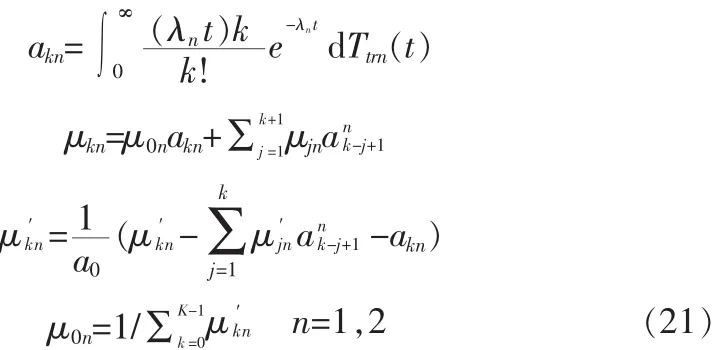
通过迭代的方法,可以求出 μ0n,并且:
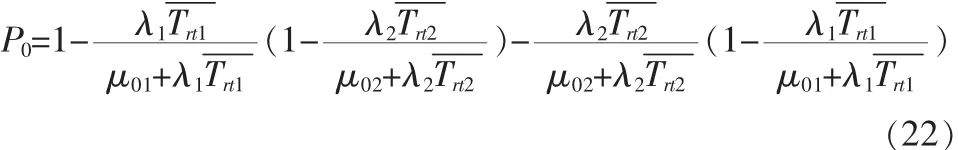
数据包的平均访问时间delay用概率母函数表示如下表达式(23):
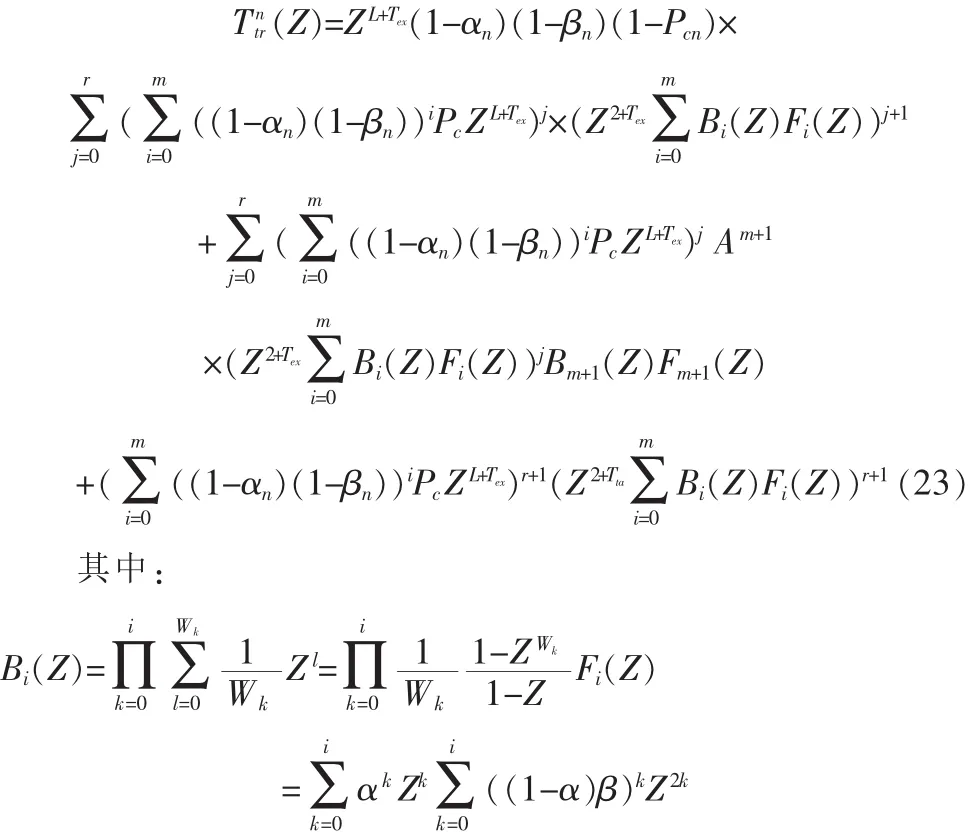
那么,数据包的传送时间的LST[3]为:
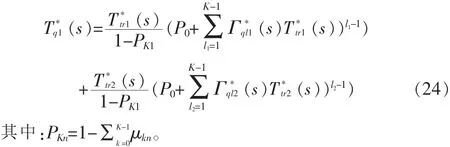
3 仿真验证
通过NS-2仿真软件来验证数据包的实时性能。参考文献[7]所述的仿真搭建我们的仿真平台。所有节点都分布在以sink节点为圆心、半径为5 m的圆内;每个节点都在彼此的传输范围内,节点的传输距离为11 m;每个节点都能侦听到其他节点的传输,也就是说不存在隐藏终端。仿真参数如表1所示。

表1 仿真参数Tab.1 Parameters for simulations
根据式(24)的分析,可以看到数据包的传送时间度量(我们将所有的时间度量归一化为backoff时间大小)与MAC参数、系统的操作点、数据包长度和缓存大小有关系。MAC的参数选取backoff计数器的初始值为m=5;backoff阶段值为23;重传计数器为r=3;数据包的长度为L=5个backoff大小。而每种情况的操作点可以根据式(18)~(20)用数学的迭代的方法计算出来。把这些参数应用在实际的仿真环境中,得到了数据包的平均传送时间,如图3所示。
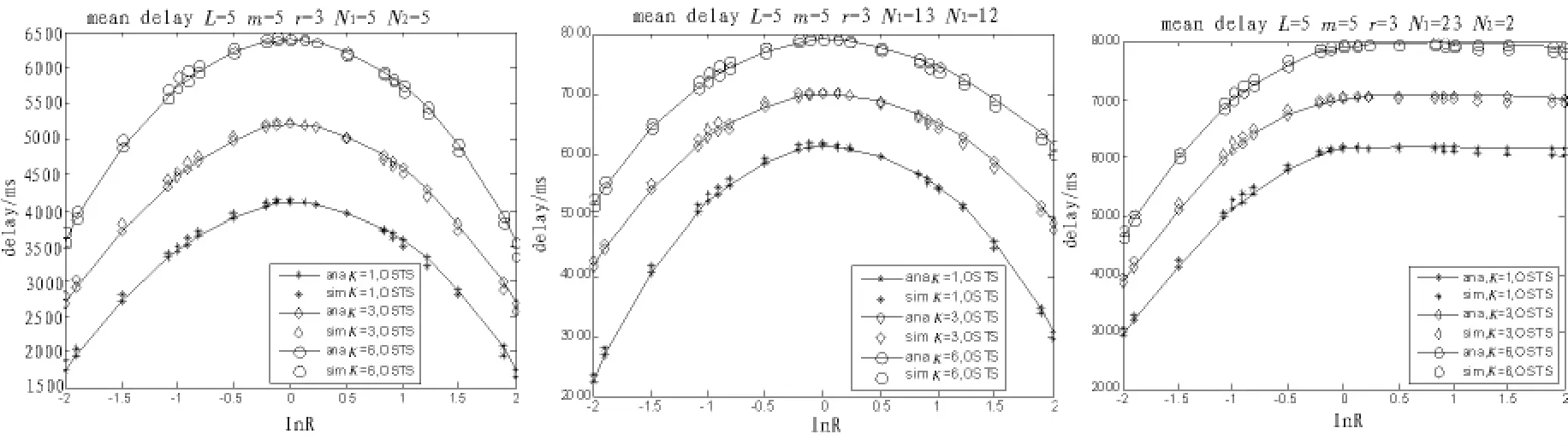
图3 数据包的平均传送时间(delay)Fig.3 Mean delay for packet transmission
取R=λ1/λ2,以其作为数据包访问时间的度量基准,并把节点数目的比例作为度量系统非均匀度即非对称度的度量,也就是说,系统的最大非均匀度即最大非对称度是两种节点的数目相当如N1=5,N2=5和N1=13,N2=12,而系统的最小非均匀度是两种节点的数目相差最大如N1=23,N2=2。从图中得到:随着节点数的增加,数据包的平均delay增加;随着非均匀度的增加,delay会增加;随着队列长度的增加,delay会增加;在R=1时,也就是两种节点的数据包到达率相同,总的数据包数λ1N1+λ2N2在不同的节点组成情况下相等,所有的delay值相同,并且delay达到最大值。从图中看出,仿真结果与分析结果是基本误差在3.251%~8.562%范围内,这个误差是可以允许的。
分析了在R=1的特殊情况下,也就是系统节点为均匀分布时的delay性能,如图4所示。随着数据包到达率的增加,队列长度小的情况如K=1,delay会缓慢增加;对于队列长度大的情况,delay增加比较剧烈;队列长度为6时,delay在λ=0.756时达到最大值。
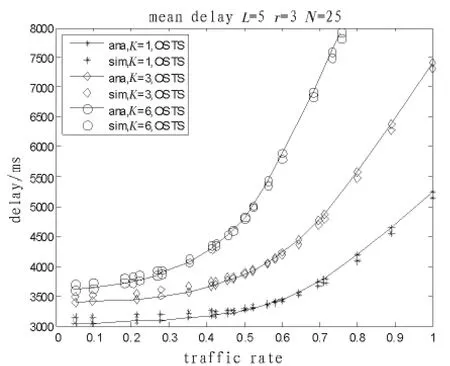
图4 两种节点均匀分布时的delayFig.4 Delay for the same traffic of two types of nodes
4 结 论
文中采用了两个半马尔可夫链和一个宏观马尔可夫链模型描述了IEEE 802.15.4标准中一种新的CSMA/CA非均匀机制OSTS,并分析提高了网络实时性能。在有限节点数和理想信道的情况下,分析了该机制在非均匀的数据包到达率和非饱和条件下各个数据包访问信道的时间性能,并且通过NS-2仿真验证了分析结果,发现文中的分析与仿真的结果是很吻合的。文中最大的特点是,数据包之间没有优先权的限制,所有包都有相同的机会访问信道,无论是同一种节点还是不同种节点之间,这是与先前分析非均匀网络[8]等中性能仅是各个节点性能的简单代数相加最大的区别。分析了两种节点在相同的数据包到达率条件下的实时性能,发现其访问时间随着到达率的增加急剧增加。
[1]Alazemi H M K,Margolis A,Choi J,et al.Stochastic modelling and analysis of 802.11 DCF with heterogeneous non-saturated nodes[J].Computer Communications,2007,30(18):3652-3661.
[2]IEEE Std 802.15.4-2006, September,Part 15.4:Wireless Medium Access Control (MAC)and physical Layer(PHY)Specifications for Low-Rate Wireless Personal Area Networks(WPANs)[S].2003.
[3]Miŝic J,Shafi S,Miŝic V B.Access delay for nodes with finite buffers in ieee 802.15.4 beacon enabled pan with uplink transmission[J].Computer Communications,2005,28(10):1152-1166.
[4]Ramachandran I,K Das A,Roy S.Analysis of the contention access period of IEEE 802.15.4 MAC[J].ACM Transaction on Sensor Networks,2007,3(1):1-29.
[5]Park P,Di Marco P,Fischione C,et al.Delay Analysis of Slotted IEEE802.15.4withaFiniteRetryLimitandUnsatu-rated Traffic[C]//IEEE Global Communications Conference,2009:1-8.
[6]Lee T T.M/G/1/N Queue with Vacation Time and Exhaustive Service Discipline[J].Operations Research,1984,32(4):774-784.
[7]Zheng J,Lee J M.A comprehensive performance study of IEEE 802.15.4[J].Sensor Network Operations,2006:218-237.
[8]Malone D,Duffy K,Leith D J.Modeling the 802.11 distributed coordination function in non-saturated heterogeneous conditions[J].IEEE/ACM Transaction Network,2007,15 (1):159-172.

