基于PARAFAC模型的新型DS-CDMA盲接收机

梁 月，刘敬浩，白 灵

（天津大学 电子信息工程学院，天津 300072）

在信号处理和通信领域，盲信号处理已经逐渐成为研究热点。盲信号处理算法能够在未知信道状态和系统参数的情况下实现对信号的检测和参数的辨识。PARAFAC（parallel factor，平行因子）方法最早是用于心理计量学和应用化学领域的一种三维数据分析方法。21世纪初，Nicholas D.Sidiropoulos将其应用到盲信号处理领域[1]。PARAFAC方法能够充分利用信号的代数性质和分集特性对接收的信号进行处理，通过三维数据的拟合得到信号处理中需要的各种参数。因其良好的性能，近几年来相继被应用到信号处理的各种领域，如阵列信号处理[2]、正交频分复用（orthogonal frequency division multiplexng，OFDM）系统[3]、多输入多输出（multi-input multioutput，MIMO）系统[4-5]。

文献[1]中提出一种性能收敛于非盲MMSE的基于PARAFAC模型的盲接收机。这种盲接收机综合利用了不同用户信号在时间、空间、扩频码方面的分集特性，在不需要已知扩频码、多径传输、DOA校准信息的情况下将用户有用信息重建出来。本文将对这种基于TALS算法的盲PARAFAC接收机进行改进，将 TALS算法与 DTLD（direct trilinear decomposition）[6]算法结合起来，提出一种新的DTALS算法，改进了TALS算法中用随机矩阵进行初始估计引起的不稳定性和收敛速度差的问题。仿真结果表明，使用DTALS算法具有更好的拟合精度和收敛速度，在一定程度上降低了算法的复杂度，提高了算法性能。

文中用到的符号与算子说明如下：diag（.）是对角化算子，表示括号中向量为对角元素形成的对角阵；⊗为Kronecker积；⊙为Khatri-Rao积，它是Kronecker积的列形式；A⊙B=[a1⊗b1，…，aRbR]；‖·‖F为矩阵的 Frobenius范数，简称 F 范数；（·）+表示矩阵 Moore-Penrose 逆矩阵；（·）T表示矩阵的转置。

1 数据模型

Nicholas D.Sidiropoulos将PARAFAC模型应用到DSCDMA系统中[1]，将接收信号构造成一个在时间、扩频、天线3个方向分集的三线性立体模型，如图1所示。

图1 DS-CDMA信号的立体方模型Fig.1 Cube model of DS-CDMA signal

假设发送端有F个用户发送数据，系统采用基带信号进行直接传输，信号经过一个加性高斯白信道进入接收端，接收端基站（BS）有I个接收天线，用码片速率对基带天线输出进行采样，总共收集到J个符号周期的数据。此时，接收端接收到的信号为：

式中，aif为用户f到天线i之间的复衰减/增益，bjf为用户f发送的第j个符号，ckf为用户f的第k个扩频码片，eijk为高斯白噪声，记 A∈CI×F为信道衰落系数矩阵，B∈CJ×F为信号矩阵，C∈CK×F为扩频矩阵，其元素分别为 aif，bjf，ckf，R∈CI×J×K为三维信号矩阵，其元素为rijk。由式（1）可知，接收信号R符合平行因子（PARAFAC）模型；矩阵A，B，C分别对应PARAFAC模型的3个模式矩阵。

在对PARAFAC模型的分析过程中，需要对三维数据R按照3个分集方向进行切片处理。R沿天线分集方向切面形式为：

其中Xi..和Ei..分别表示在天线方向上的三维数据X和E的第i层矩阵，A（i）表示信道衰落矩阵的第i行。将Xi..按行排列，可以得到紧凑的数据形式

EX为天线切面噪声，按照式（2）和（3）的方法，将三维数据R沿其时间分集和扩频分集方向进行切面操作，得到切面形式 Y 和 Z 如式（4）和（5）所示：

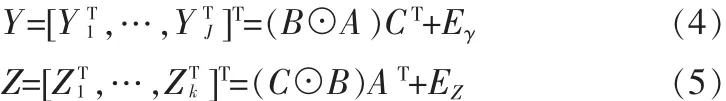
根据文献[1]可知，在一定条件下，PARAFAC模型能够唯一分解。

2 DTALS-PARAFAC接收机

文献[1]中提出的TALS-PARAFAC盲接收机性能上接近于最小均方误差接收机。TALS-PARAFAC算法中使用随机矩阵来初始化矩阵 A、B，基于式子（3）、（4）、（5），根据最小二乘原理迭代实现PARAFAC模型的三线性分解。然而当初始矩阵A、B估计不当时，迭代过程容易陷入局部最优的计算“沼泽”，收敛相当缓慢，并可能产生错误的解。

DTLD（direct trilinear decomposition）是一种直接三线性分解方法，也是一种基于PARAFAC模型的三维分解方法，它是非迭代的，具有直接快速的优点[7]。但是没有明确的最优化界限，在信噪比不高的情况下，若三维数据不严格服从三线性模型或随机误差较大，有可能出现无意义的虚数解，可靠性差。

在应用化学领域，已有学者提出并验证，在基于PARAFAC模型的分析化学算法中，使用适当的初始值对矩阵进行初始估计（如奇异值分解矩阵、特征分析）可以有效地提高算法的收敛速度和拟合精度[8]。因此，在基于PARAFAC模型的TALS算法中融入DTLD算法，能够解决TALS算法中初始值选取不当导致的收敛缓慢并且可能出现错误的解的问题。仿真结果表明，使用DTLD对TALS算法进行初始化，不仅能够提高原本算法的收敛速度，而且能够在一定程度上提高算法的精度，使分解出的数据更加接近于真实数据。

3 基于DTLD的交替最小二乘算法

步骤 1 根据式（3）、（4）、（5）3 个切面方程进行奇异值分解，其中U、V取前F个左奇异值矢量，W取前两个左奇异值矢量。

步骤 2 根据式（9）、（10）构造伪样本矩阵 G1、G2，其中wk1、wk2代表矩阵W的第一列和第二列。

步骤3 使用QZ分解G1、G2组成的特征方程，L、M分别为方程的特征向量，可证明 A、B 矩阵由式（11）、（12）得到[7]。

步骤4 根据式 （4），利用最小二乘准则得到C的估计值，如式（13）所示。

步骤5 根据式（3）和步骤4求得的C的估计值利用最小二乘准则得到A的估计值，如式（14）。

步骤6 根据式（5）和步骤4、5求得的A、C的估计值利用最小二乘准则得到B的估计值，如式（15）。步骤7 重复步骤4～6，直至算法收敛即：

其中ε为一个很小的值（通常取1e-6）。

算法收敛后，得到估计矩阵A、B、C。DTALS算法利用步骤1、2、3得到的矩阵进行迭代初始化，使初始值更加精确，能够减少迭代的次数，降低运算的复杂度。仿真结果表明，DTALS算法在拟合精度上比原有的TALS算法有所提高，并且具有更快的收敛速度。

4 仿真结果与分析

通过仿真，分析DTALS-PARAFAC接收机的误码率（bit error rate，BER）性能和收敛性能[9]，将仿真精度与仿真速度等因素综合考虑，假设M=4个用户的DS-CDMA系统，一次处理的用户信息样本长度为I=50，扩频码采用Hadamard码，长度为K=7，天线数J=4，噪声为加性高斯白噪声，用户与天线的衰落因子服从高斯随机分布。Monte Carlo仿真1 000次取其平均误码率。

4.1DTALS-PARAFAC、TALS-PARAFAC、MMSE 接 收机的BER性能比较

将DTALS-PARAFAC盲接收机与文献 [1]中TALSPARAFAC接收机的误比特率性能比较。同时对非盲的线性MMSE接收机进行仿真以作参考。MMSE接收机需要已知信道衰落矩阵A和扩频码矩阵C。仿真结果如图2所示。

图2 3种接收机的BER性能比较Fig.2 BER curves comparison of three receivers

由图2可以看出，在未知信道衰落矩阵A和扩频码矩阵C的基础上，DTALS-PARAFAC接收机的性能要优于TALSPARAFAC接收机，且与非盲MMSE接收机性能相近。说明基于PARAFAC的盲接收机性能优越，两种算法的误码性能反映了其迭代算法的拟合精度，即接收机的误码率越低，拟合精度越高，反之亦然。因此，在多用户DS-CDMA系统中，DTALS算法拟合精度更高[10]。

4.2DTALS-PARAFAC接收机和TALS-PARAFAC接收机的收敛速度比较

图3给出了在不同信噪比条件下，两种接收机的平均迭代次数。可以看出2种接收机的迭代次数均随着信噪比的增加而下降.在相同信噪比的情况下，DTALS-PARAFAC的迭代次数远小于TALS-PARAFAC接收机。因此，在保证误码率的前提下，DTALS算法具有更优越的收敛速度，性能更加稳定。

图3 2种接收机收敛性能比较Fig.3 Convergence performance comparison of two receivers

5 结 论

文中将PARAFAC模型与多用户多天线DS-CDMA系统相结合，在原有的TALS算法的基础上结合一种DTLD算法，提出了一种新的DTALS-PARAFAC盲接收机，通过DTLD算法将更加符合模型分解的初始值引入到TALS迭代过程中，优化了算法的性能。结果表明，DTALS-PARAFAC接收机在处理DS-CDMA信号的过程中具有更好的拟合精度和收敛速度，更适用于DS-CDMA系统。

[1]Sidiropoulos N D，Giannakis G B，Bro R.Blind PARAFAC receivers for DS-CDMA systems[J].IEEE Transactions Signal Processing，2000，48（3）：810-823.

[2]Sidiropoulos N D，Bro R，Giannakis G B.Parallel factor analysis in sensor array processing[J].IEEE Transactions Signal Processing，2000，48（8）：2377-2388.

[3]JIANG Tao，Sidiropoulos N D.A direct blind receiver for SIMO and MIMO OFDM systems subject tounknown frequency offset and multipath[J].4th IEEE Workshop on Signal Processing Advances in Wireless，2008，56（1）：111-124.

[4]Acar T，YU Yuan-ning， Petropulu A P.Blind MIMO system estimation based on PARAFAC decomposition of higher order output tensors[J].IEEE Transactions on Signal Processing，2006，54（11）：4156-4168.

[5]YU Yuan-ning，Petropulu A P.PARAFAC-based blind estimation of possibly underdetetermined convolutive MIMO systems[J].Transactions on Signal Processing，2008，56（1）：111-124.

[6]Tomasi G，Bro R.A comparison of algorithms for fitting the PARAFAC model[J].Computational Statistics SNR/dB&Data Analysis，2006（50）：1700-1734.

[7]Sanchez E，Kowalski B R.Tensorial resolution：a direct trilinear decomposition[J].Journal of Chemometrics，1990，4（1）：29-45.

[8]Sinha A E，Fraga C G，Prazen B J，et al.Trilinear chemometric analysis of two-dimensional comprehensive gas chromatography-time-of-flight mass spectrometry data[J].Journal of Chromatogry A，2004（1027）：269-277.

[9]王铮一，郑文杰.基于基因表达式编程的变压器故障诊断[J].陕西电力，2012（4）：82-85.

WANG Zheng-yi，ZHENG Wen-jie.GEP-based transformer fault diagnosis[J].Shaanxi Electric Power，2012（4）：82-85.

[10]祝佳宁，舒怀林.计算机控制与自动化仪表综合实验平台的研究[J].工业仪表与自动化装置，2012（2）：52-54，58.

ZHU Jia-ning，SHU Huai-lin.The research of the comprehensive experiment platform of computer control and automation instrumentation[J].Industrial Instrumentation&Automation，2012（2）：52-54，58.