基于Contourlet域HMT模型的CycleSpinning去噪方法

李 康，陈雪军，刘 冰，胡湘江，石 湘

（中国卫星海上测控部 江苏 江阴 214431）

Contourlet变换[1]作为解决张量积小波变换角分辨有限问题而产生的一种二维信号多尺度几何分析新工具，同时具备高度的方向性和极低的冗余度两种特征，可以良好地刻画二维信号中曲线奇异性，从而为图像处理提供了新的有力工具。笔者对Contourlet域隐马尔可夫模型（HMT）图像去噪方法[2]进行了深入的研究，并将Cycle Spinning[3]引入到去噪得过程当中，提出了基于Contourlet域HMT模型的Cycle Spinning去噪方法，并通过测试图像验证了其优越性。

1 Contourlet域HMT模型

小波域隐马尔科夫树（HMT）模型[4]采用混合高斯模型刻画各子带系数的概率分布，并通过小波系数隐状态在多个尺度之间的Markov依赖性来刻画小波系数随尺度的持续性（Persistence）和尺度内位置上的聚集性（Clustering），从而可以有效地捕捉小波系数之间的关系，但是由一维小波通过张量积而形成的二维可分离小波变换只具有有限个方向，不能有效表达含线奇异的二维信号。Do和Vetterli提出的Contourlet变换[1]能够很好地表征二维信号的各向异性特征，更好地捕捉二维信号的方向信息，在Contourlet域建立HMT模型可以有效地描述各方向信息之间的关系。在Contourlet域HMT模型[2]中，采用Contourlet系数对应的隐状态变量来体现系数之间的Markov相关性，系数之间的依赖关系由父子状态变量之间的状态转移概率体现。在Contourlet域HMT模型中，某个方向子带中的父节点可以和多个方向子带中的子节点相连，如图1所示，图中黑色方框表示父节点系数，白色方框表示其子节点系数；所以，和二维张量积小波域HMT模型相比，Contourlet域HMT模型不仅可以很好地描述各系数在位置上的聚类性和尺度间的持续性，而且还可以有效表达不同方向上的系数之间的依赖性。

图1 张量积小波域和Contourlet域HMT模型的父子关系对比Fig.1 Compare separate wavelet transform HMT model with Contourlet domain HMT model

若用（j，k，i）表示j尺度下，第k个方向的第i个系数所对应的节点，j=1代表最粗尺度，m，n表示状态，用M状态零均值高斯混合模型来刻画各子带系数的非高斯性，则Contourlet 域 HMT 模 型 可 由参数 θ=[p（1，k，i），m，p（j，k，i），（m，n），σ2（j，k，i），m]描述，其中：

1）：p（1，k，i），m（k=1，…K1；m=1，…，M）：根节点（1，k，i）处于状态m的概率，K1为最粗尺度下的方向数目。

2）p（j，k，i），（m，n）（ j=2，…，J；k=1，…Kj；m，n=1，…，M）：在 节 点的父节点处于状态n的条件下，节点（j，k，i）处于状态m的条件概率，即状态转移概率，J为LP变换的尺度数，Kj为j尺度下的方向子带数。

3）σ2（j，k，i），m（j=1，…，J；k=1，…，Kj；m=1，…，M）：节点（j，k，i）处于状态m时所对应的方差。

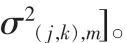
EM算法[4]是训练HMT模型的有效方法，任务是估计HMT模型参数θ，对于Contourlet域HMT模型，EM算法收敛于Contourlet系数集W的似然函数f（W）的局部最大值，其迭代步骤如下：

1）初始条件：选择一个初始模型估计θ0；设置迭代数l=0。

2）E步：用上行-下行算法[4]计算下列条件似然函数β和关联概率函数α：

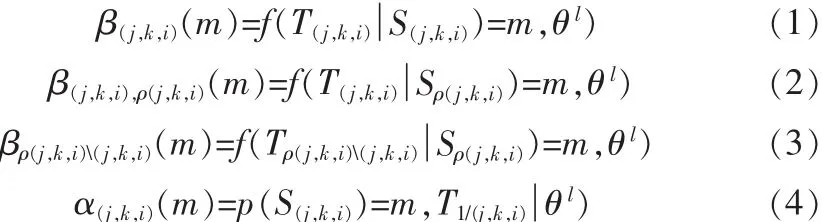
其中，ρ（j，k，i）表示节点（ j，k，i）的父节点，T（j，k，i）是以节点（j，k，i）为根节点的子树，S（j，k，i）表示节点（j，k，i）的状态变量 ，m 是 状 态 ，T1（j，k，i）是 从 节 点 （j，k，i） 所 在 的 树 中 去 除 T（j，k，i）的 剩 余 部 分 ，Tρ（j，k，i）（j，k，i）是 从 子 树 Tρ（j，k，i）中 去 除 T（j，k，i）的 剩 余部分。

根据这些概率函数，可以采用下式计算隐状态概率：

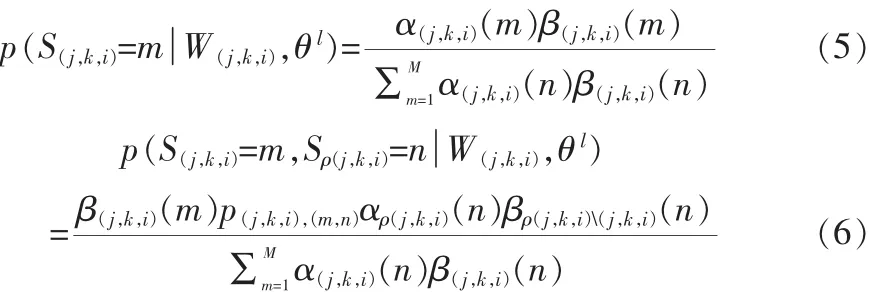
其中，W（j，k，i）表示节点（j，k，i）所在树的 Contourlet系数集。

3）M步用来更新各HMT参数，将各子带内的节点进行捆绑，则M步为：

其中，Z（j，k）表示 j尺度、k 方向子带内 Contourlet系数的个数，w（j，k，i）是节点（j，k，i）处的 Contourlet系数。

4）若收敛，则完成HMT参数的训练，否则令l=l+1，回到步骤 2）。

2 基于Contourlet域HMT模型的去噪法

含有零均值高斯白噪声的二维信号在Contourlet域可表示为：

其中 u（j，k，i）、v（j，k，i）和 e（j，k，i）分别表示无噪信号系数、含噪信号系数和噪声系数。 去除噪声的主要任务是用 v（j，k，i）来估计u（j，k，i），基于 Contourlet域 HMT 模型的去噪方法如下：

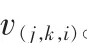
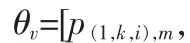
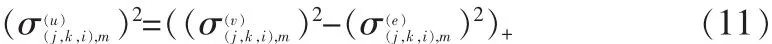
式中，x≥0 时，（x）+=x；x<0 时，（x）+=0。 θu的其他参数和 θv的相同。

4）用式（12）得到 u（j，k，i）的估计值：

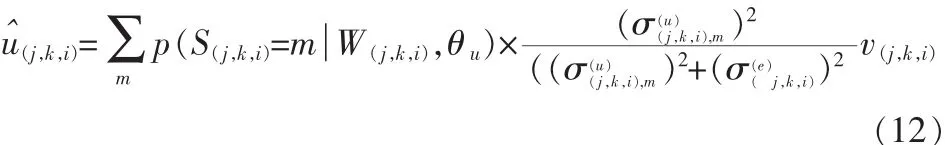
3 本文去噪方法

Cycle Spinning是克服变换缺乏平移不变性有效的方法，一般用在变换的阈值去噪过程中以减少失真和假象[3]。在此处我们将它引入到Contourlet域HMT模型的去噪过程当中，给出了一种基于Contourlet域HMT模型的Cycle Spinning去噪方法，该方法可表示如下：

式中： 其中，X 为原始含噪二维信号，Sx，y和 S-x，-y为二维平移和逆向平移算子，（K1，K2）是信号在两个方向上的最大平移量，CHMD表示基于Contourlet域HMT模型的去噪方法，yˆ是去噪后的信号。

4 实验结果

选择 512×512大小的标准图像 Lena、Zelda、Barbara叠加均值为零的高斯白噪声进行实验，噪声标准差取σ=30，40，50，状态数 M 取 2，在 Contourlet变换中，采用 4 尺度LP变换，从最细尺度到最粗尺度，每个尺度下的方向数目依次取 8、8、4、4。 LP 变换采用“9-7”双正交滤波器，方向滤波器组（DFB）采用由 Phoong等[5]设计的“23-45”双正交梅花滤波器组。实验对比了4种去噪方法：小波萎缩阈值去噪法（VisuShrink）[6]、小波域 HMT 模型去噪方法（WHMTD）、Contourlet域HMT模型的去噪方法（CHMTD）和基于Contourlet域HMT模型的Cycle Spinning去噪方法（CHMTD-CS）。

表1给出了使用不同方法降噪后图像的PSNR值。可以看到，CHMTD-CS的去噪效果最佳，而WHMTD和CHMTD具有相近的PSNR值，这些基于HMT的去噪方法都比VisuShrink好。

表1 不同去噪方法的PSNR值（单位：dB）比较Tab.1 Compare of PSNR values with different denoising methods

将σ=30时去噪后的Lena局部图像显示在图2和图3中，图3显示的是图 的一个放大的细节，以利于读者更好地观察不同方法的差异。可以看到，VisuShrink产生了过多的假象和失真，造成严重的细节模糊；和WHMTD相比，CHMTD和CHMTD-CS可以更有效地保持含噪图像中的可视细节（包括帽子、头发和眼睛上的纹理和边缘）；此外，CHMTD中的细小失真在CHMTD-CS中得到明显的削弱，使得消噪后的图像和原始图像更一致。综上分析，不管是从PSNR值还是从视觉效果来衡量，CHMTD-CS都具有最优的去噪效果[7]。

图2 不同去噪方法对Lena图像的（σ=30）的去噪结果Fig.2 Denoising results of the Lena image corrupted with a Gaussian noise of σ=30

图3 图2的放大细节Fig.3 amplified details of Fig.2

5 结 论

本文介绍了基于Contourlet域HMT模型的随机噪声衰减方法，用Cycle Spinning克服Contourlet缺乏平移不变性的缺陷，改进了该算法，用测试图像算例验证了改进后算法的合理性和有效性。

[1]Do MN，Vetterli M.The contourlet transform：An efficient directional multiresolution image representation [J].IEEE Transactions on Image Processing，2005，14（12）：2091-2106.

[2]Po DDY，Do MN.Directional multiscale modeling of images using the contourlet transform[J].IEEE Transactions on Image Processing，2006，15（6）：1610-1620.

[3]Fletcher AK，Ramchandran K，Goyal VK.Wavelet denoising by recursive cycle spinning[C]//International Conference on Image Processing，2002（2）：873-876.

[4]Crouse MS，Nowak RD，Baraniuk RG.Wavelet-based statistical signal processing using hidden Markov models[J].IEEE Transactions on Signal Processing， 1998， 46 （4）：886-902.

[5]Phoong SM，Kim CW，Vaidyanathan PP，et al.A new class of 2-channel biorthogonal filter banks and wavelet bases[J].IEEE Transactions on Signal Processing，1995，43 （3）：649-665.

[6]Mallat S.A wavelet tour of sinal processing[M].2nd ed.New York：Academic，1999.

[7]祝磊.基于TLS-ESPRIT的系统低频振荡模态参数提取方法[J].陕西电力，2012（3）：43-46.

ZHU Lei.Model parameters extracting method of lowfrequency oscillations in power systems based on TLS-ESPRIT[J].Shaanxi Electric Power，2012（3）：43-46.