基于ANSYS的大伙房水库土坝渗透系数反演
佟晓娜
(辽宁省大伙房水库管理局,辽宁抚顺 113007)
1 概述
由于大坝边界条件的复杂性和坝体、坝基渗流的非均匀性,用渗流基本方程计算成果难以与大坝实际运行情况相一致,因此有必要通过渗流监测资料反演其渗透系数。即在渗流资料分析基础上,选取一段库水位相对稳定时间的大坝渗流监测资料,开展大坝稳定渗流反演分析。本文根据温度场和渗流场的相似性,利用有限元分析软件ANSYS的热分析功能计算土石坝渗流问题,通过ANSYS的优化设计功能,建立了基于ANSYS的渗透系数反演模型,反演得到大坝稳定渗流后的心墙料的渗透系数。
2 工程概况
大伙房水库是我国“一五”期间修建的重点水利工程,具有防洪、供水、灌溉、养鱼、发电等多种功能,是新中国成立后我国第一座自行设计、自行施工的大型水利枢纽工程。
水库主坝为碾压式黏土心墙坝,心墙顶部宽度为2.25 m,心墙底部宽度为15.0 m,心墙顶部高程为136.8 m。黏土心墙底部为混凝土截水墙,底座宽1.0 m,墙底宽0.7 m,顶宽0.5 m,墙身高2.0 m。坝顶宽8 m;坝顶高程139.8 m,防浪墙顶部高程141.0 m。
3 稳态温度场与稳定渗流场的相似性
土石坝渗流基本微分控制方程如下:
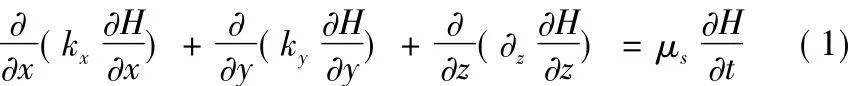
式中:H为总渗透水头;kx,ky,kz为以 x,y,z轴为主方向的渗透系数;μs=ρg(α+nβ)为单位贮水量或贮存率。
稳态热传导基本微分控制方程如下:
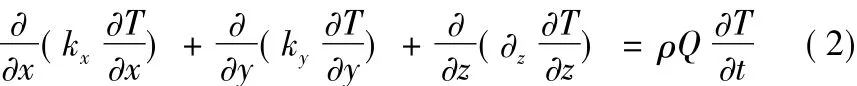
式中:T 为温度;kx,ky,kz为以 x,y,z轴为主方向的介质热传导率;ρQ是热容量。
通过式(1)与式(2)比较可以看出,土体渗流问题与温度场问题的控制方程非常相似,只需要将温度场介质换成土体介质,相应的参数换为求解渗流场的参数,因此温度场和渗流场是相似的。值得注意的是,当渗流变为稳定渗流时,则单位贮水量μs=0,而令稳态热传导时的Q=0时,则土石坝稳定渗流基本微分方程与稳态热传导方程完全一致,参数及边界条件相互对应,为应用ANSYS热分析模块进行渗流场分析奠定了基础。
4 原始资料选取
选取水库主坝设有心墙测压管的0+500断面对大伙房水库大坝心墙渗透系数进行反演,该断面测压管经工程多年运行实践表明,渗流状态比较稳定,没有堵塞与不灵敏等现象,个别异常数据进行剔除或调整后,监测数据可以用于分析使用。为了正确反映大坝渗流的实际情况,选取2006年至2009年所观测的平均上游水位(125.09 m)进行正分析计算,监测资料选取其所对应的测压管水位值。
所选0+500断面测压管布置图见图1所示,测压管水头数据见表1。

图1 渗流监测点布置图
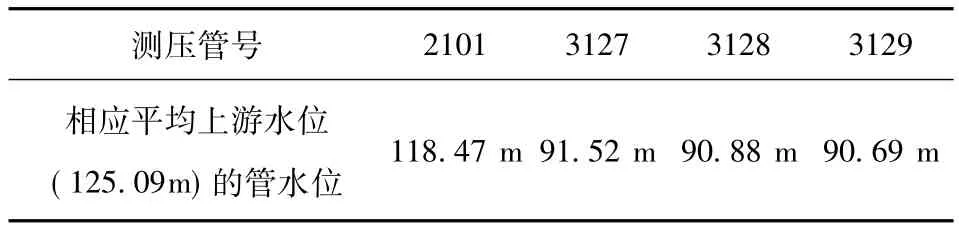
表1 断面的测压管实测水位值
采用间接法计算,预先假定渗流场各个分区材料的渗透系数。土坝中部分分区材料的渗透系数比较稳定,与设计时出入不大,对这些区域无需进行反演,计算时直接采用设计值。正分析计算中其它分区渗透系数取设计值,见表2所示,而仅对黏土心墙的渗透系数进行反演。

表2 渗透系数分区表
根据流量守恒原理可知,各材料分区满足一定比例的任意渗透系数都能适应给定的水头函数,故反求得出的渗透系数的绝对值是任意的,但本次计算中假定某些渗透系数为已知值,所以反演结果是唯一的。
5 反演断面有限元模型
取坝段上游水位以下的坝体表面、坝基侧面、坝段下游水位以下坝体表面、坝基侧面为第一类边界(定水头边界),大坝坝基的上下游侧面、底边界为第二类边界(无流量交换),坝段上游水位以下的坝体表面及坝基下游表面为第一类边界(定水头边界)。整个模型共划分3 652个节点,3 471个单元,见图2。

图2 0+500断面分区图

图3 0+500断面单元划分图
6 反演结果及分析
设定黏土心墙渗透系数初始值为1.7×10-8cm/s,利用ANSYS优化设计方法得到的反演结果见表3。取黏土心墙渗透系数目标函数最优反演值k=1.36×10-8cm/s对坝体0+500断面进行二维稳定渗流有限元计算,提取该断面测压管所在位置的计算值与实测值对比见表4。
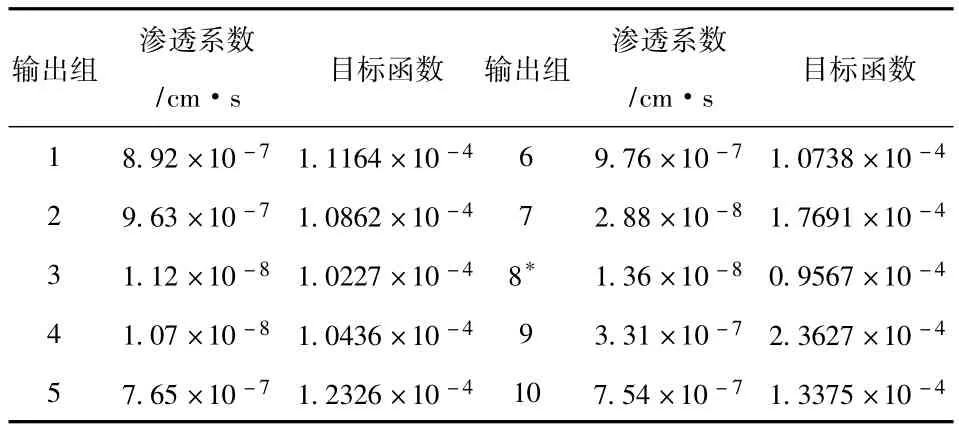
表3 黏土心墙渗透系数优化反演结果
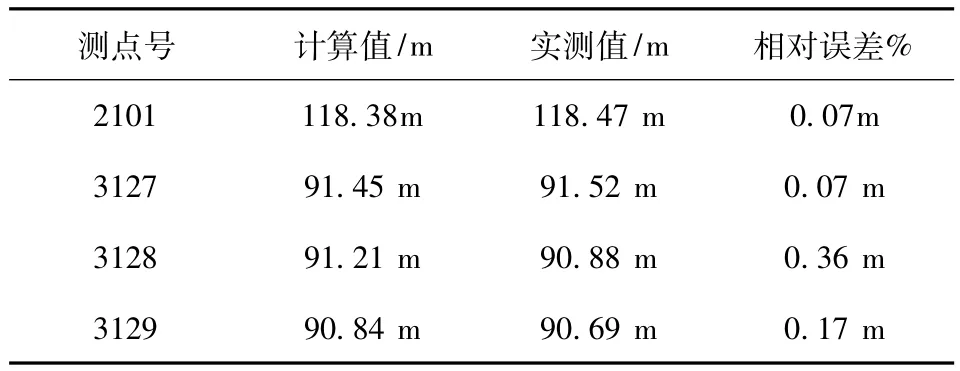
表4 测压管水位计算值与实测值对比(上游水位125.09m)
计算值与实测值的对比表明,有限元计算值与实测值相对误差较小,拟合结果能够满足精度要求。同时,也表明所求得的渗透系数比较合理,可以用于渗流数值计算。
综上可见,使用ANSYS优化模块进行渗透系数反演分析,计算过程简洁,计算速度较快。但是,当初始值作较大变动时,得到的优化值亦会有较大的变动,这与反演时所参照的监测点个数有关,增加监测点个数可将反演参数约束在一个较稳定的范围。
7 基于ANSYS方法的模型可靠性论证
为了验证反演的力学参数是否正确,再次采用正分析方法把反分析出的参数值代入到ANSYS所建立的模型中进行计算,在上游水位为正常蓄水位、防洪限制水位2种不同工况下,对有限元模型进行计算。计算成果见表5。
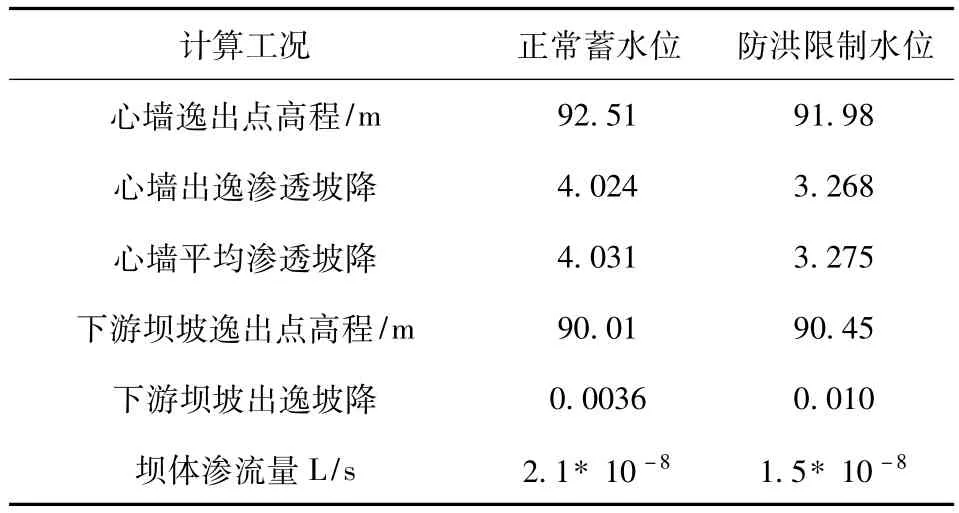
计算工况 正常蓄水位 防洪限制水位心墙逸出点高程/m 92.51 91.98心墙出逸渗透坡降 4.024 3.268心墙平均渗透坡降 4.031 3.275下游坝坡逸出点高程/m 90.01 90.45下游坝坡出逸坡降 0.0036 0.010坝体渗流量L/s 2.1*10-8 1.5*10-8
提取测压管所在结点渗压值与实测管水位进行对比,对比结果见表6。由表6可见,渗压计算值比实测值稍小,这可能是因为在计算时未考虑地下水位对渗流的影响,数值计算结果与实测值相对误差较小。
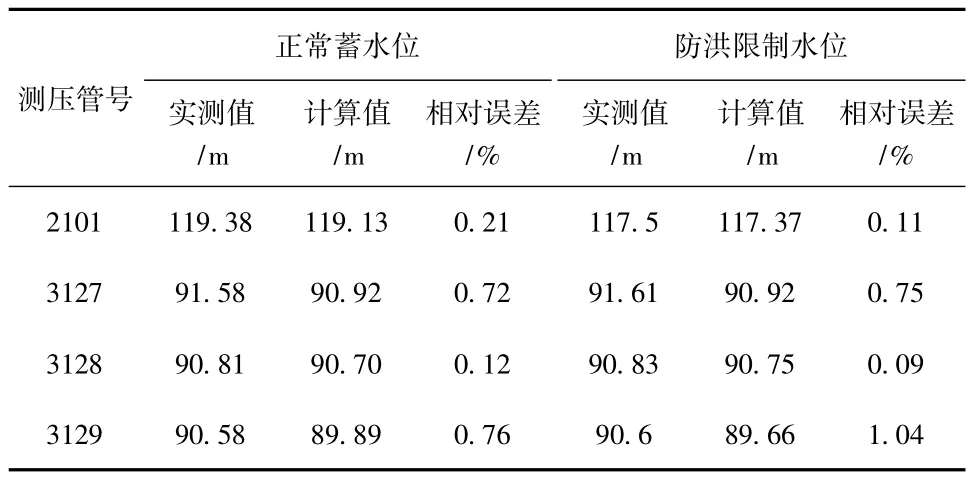
表6 0+500断面渗压计算值与实测值对比
8 结语
综上可见,使用ANSYS优化模块进行渗透系数反演分析,计算过程简洁,计算速度较快。但是,当初始值作较大变动时,得到的优化值亦会有较大的变动,这与反演时所参照的监测点个数有关,增加监测点个数可将反演参数约束在一个较稳定的范围。利用ANSYS的优化设计功能,反演得到更符合大伙房水库大坝实际工况的渗透系数,利用这个渗透系数进行渗流数值计算,通过对计算值与实测值的对比表明,有限元计算值与实测值相对误差较小,拟合结果能够满足精度要求。说明所求得的渗透系数比较合理,可以用于渗流数值计算。
[1]王俊,刘进宝,韩剑,等.基于人工神经网络的混凝土大坝渗透系数反演[J].华北水利水电学院学报,2003,24(3):9-12.
[2]刘先珊,费文平,张林.一种大坝渗透系数分区反演新方法研究[J].岩土力学,2004(11):25.
[3]周志芳,朱学愚.确定岩体渗透参数的结构面控制反演法[J].南京大学学报,1999,35(3):316 -321.

