遗传算法及其在油料保障路径优化中的应用研究
曹 刚,张仁平
(1.解放军76167部队 保管队,广东 韶关512133;2.解放军后勤工程学院军事油料应用与管理工程系,重庆401311)
0 引言
在部队行军、交通运输、市政规划、最优选址等诸多方面,往往会遇到网络最优化问题,即路径优化类问题,其核心是求最短路径,包括含权路(指道路质量、类别、安全等所含不同的权重系数,下同)的最短路径。油料保障路径优化与其它路径优化问题存在不同之处:一是不仅仅要找一条最短路,很多时候需要同时找出最短路或次短路,为指挥员决策作参考;二是有时不仅要知道两个定点的最短路,而且要知道某个定点到其它定点的最短路径;三是路径优化中可能寻找排除某一条或几条道路(可能被炸毁、冲毁)之后的最短路,这就需要在最短路中增加一些附加条件。因此,许多路径探索的传统经典优化算法,典型的有Dijkstra算法、Bellman-Ford-Moore算法、A*(也可读作 A 星)算法等等[1],对于油料保障路径优化问题则显得有些力不从心。
遗传算法是解决搜索问题的一种通用算法,其共同特征是:1)首先生成一组候选解;2)依据某些适应性条件计算候选解的适应度;3)根据适应度决定保留或放弃候选解;4)对保留的候选解进行遗传操作,生成新的候选解。遗传算法上述特征以一种特殊的方式组合在一起:基于染色体群的并行搜索。这就使得遗传算法区别于其他搜索算法,像油料保障路径优化类的路径探索,遗传算法就是一个很好的选择。
1 遗传算法的基本概念
1.1 遗传算法基本概念
遗传算法(Genetic Algorithm,简称GA)是模仿达尔文生物进化论和孟德尔遗传学机理的随机全局探索和优化方法,适合于解决复杂系统优化问题。遗传算法作为一种实用、有效、鲁棒性强、适应性好的优化算法,近年来发展极为迅速,已在函数优化、组合优化、生产调度、自动控制、机器人学习等方面得到广泛应用[2]。
下面介绍遗传算法常用的几个基本概念。
1)染色体(Chromosome):染色体由基因组成的遗传信息的载体,基因是指用一位二进制代码(0或1)表示的一个遗传因子,基因的数量就是染色体的长度。使用遗传算法时,需要首先明确染色体编码规则,明确基因的长度,把问题的解变成染色体。一个染色体就代表问题的一个解。
2)群体(Population):每代染色体的集合称为群体,群体中染色体的数量称为群体的大小。使用遗传算法时,根据问题设置群体的大小,一般可设置为10或20。
3)适应度(Fitness):各个个体对环境的适应程度叫做适应度。为了体现染色体的适应能力,引入了对问题中的每一个染色体都能进行度量的函数,叫适应度函数,也是问题的目标函数。
1.2 遗传算法基本原理
遗传算法类似于自然进化,通过寻找好的染色体来求解问题。与自然界相似,遗传算法对求解问题的本身一无所知,它所需要的仅是对算法所产生的染色体进行评价,使适应度高的染色体有更多繁殖机会。在遗传算法中,通过随机方式产生若干个染色体,即假设解,形成初始群体;通过适应度函数对每个个体进行评价,淘汰低适应度的个体,选择高适应度的个体进行选择、交换和突变等遗传操作,经过遗传操作后的个体集合形成下一代新的种群,依次类推。
1.3 遗传算法基本步骤
最简单的遗传算法操作主要有三种:选择(selection),交换(crossover)和突变(mutatiun)。
1)选择操作:从群体中选择某些染色体用于繁殖后代(生成新的候选解),染色体的适应度越高,它被选中的概率就越大。
2)交换操作:随机地选定一个位置,将两个染色体在该位置上交义互换,得到两个后代。例如,两个染色体分别为100和111,随机选定的位置是第二位,进行交换的结果是110和101。
3)突变操作:随机改变染色体中某一位置上的遗传因子的值。例如,二进制串011在第二位上发生突变,变成001。突变可能发生在染色体的任意位置基因上。通常发生突变的概率很小。
从表现型到基因型的映射称为编码。遗传算法在进行搜索之前,先将解空间的解表示成遗传空间的染色体,这些基因的不同组合就构成了不同的解。假设一个问题,设定染色体的长度为m,遗传算法的基本步骤可以简单地描述为:
1)随机生成n(最好是偶数)个长度为m的染色体,形成初始群体。
2)将群体中每个染色体串代入适应度函数,计算适应度。
3)判断是否满足算法终止条件,若是,则适应度最大的染色体对应的候选解就是最优解或满意解;若否,则转步骤4。
4)进行下列步骤产生下一代群体
①在当前的染色体群中随机选取n个染色体作为父体,选取染色体的概率等于该染色体的适应度除以群体的适应度总和。在选取父体的过程中,一个染色体可以被多次选中。
②对于选中的父体,按照交换概率算出需要交换的染色体数量(如果需要交换的染色体数量是奇数,则要增选一个交换个体或删去一个个体,使交叉对象成对出现)。发生交换的位置是随机的,每个位置的概率是相同的。在遗传算法中有时会用到多点的交换,即在多个随机的点上发生交换。
3)对于选中的父体,按照突变概率算出需要突变的染色体数量,分别在每个染色体的随机位置进行,每个位置的概率是相同的。
5)转向步骤2
每次迭代这一过程称为一个世代,一个遗传算法的应用通常需要迭代50~500个世代,可以指定迭代的世代数作为算法的终止条件。
2 油料保障路径优化的实现
用遗传算法解决油料保障路径优化问题,其核心就是首先生成一组染色体(候选最优路径),根据指挥员意图确定目标函数,计算染色体的适应度,再根据适应度决定保留或放弃染色体,并对保留的候选解进行遗传操作,生成新的候选解,依次循环,找到一个或一组最优解。
为了便于算法的理解和实现,下面举个例子加以说明。

图1 油料保障实体所在区域路网示意图
若交换概率为0.2,变异概率为0.01,用遗传算法求图1的从U0到U7的最优路径。
2.1 染色体编码
按照U0到U7各个顶点(除U0和U7)依次排序,作为染色体的基因排序,一个顶点对应一个基因,当基因为1时,表示该顶点进入最优路径;为0时则退出最优路径。染色体中不为0的基因排序就是各顶点在最优路径中出现的顺序,染色体的长度等于图中的顶点数。
2.2 适应函数
对于图1,属于图论中典型的n个顶点m条边的路网图G,假设相邻两顶点 Ui、Uj边长为d(Ui、Uj),假设从U0到U7之间连通路径的长度定义为算法适应函数f,则

i,j(i≠j)为染色体中不为0的基因在染色体中对应的位置,路径优化就是使得f最小的满意路径。
2.3 产生初始群体
初始群体是遗传算法搜索最优的出发点。群体规模越大,搜索的范围越广,但是每代的遗传操作越长,反之亦然。通常,M取50~100。初始群体中的每个个体是按随机方法产生的。对于上例,为了便于说明,假设只产生10个初始个体,个体为6位的0/1随机数,组成一个初始个体。
C1=011110,C2=001001,C3=000110,C4=111001,C5=101000
C6=011001,C7=101101,C8=001100,C9=111101,C10=101010
2.4 适应度计算(个体评价)
将群体中每个染色体串代入适应度函数,计算适应度。以C1为例,011110代表候选优化路径为{U0、U2、U3、U4、U5、U7},由于 U4不能直接联络到U5,其适应度为∞,即 f(C1)=∞,以 C2为例,001001 代表候选优化路径为{U0、U3、U6、U7},f(C2)=15,依次计算,f(C3)=∞,f(C4)=∞,f(C5)=∞,f(C6)=15,f(C7)=22,f(C8)=22,f(C9)= ∞,f(C10)=13。从以上数据可看出,C4最健壮,C1、C3、C4、C5、C9最虚弱。
2.5 复制选择
显然,个体适应度愈高,被选中的概率愈大。但是,适应度小的个体也有可能被选中,以便增加下一代群体的多样性。近年来,在遗传算法中常常采用择优选择法。这种方法没有明显的复制操作,而是根据个体的相对适应度,反复地从群体中选择M个个体组成下一代群体。当然,个体的适应度愈高,它被重复选中的可能性愈大,而重复选中的就相当于复制。相反适应度小的个体往往未能选中,它就被淘汰,其操作过程为:
1)计算各染色体Ci的适应度f(Ci),
2)计算群体的适应度的总和Sn:
3)用Sn减去各个体适应度的差除以Sn,得相对适应度,进行归一化处理就成为该个体被选中的概率
累计pi得累计概率gi:
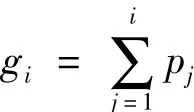
4)产生[0,1]均匀分布的随机数r;
5)将r与gi相比较,若gi-1<r<gi,则选个体 i进入下一代新群体;
6)反复执行(4)及(5)项,直至新群体的个体数目等于父代群体规模,本例中为10。
对于本例中,若取1000为∞,则第一代种群的适应度总和Sn=1000+15+1000+1000+1000+15+22+22+1000+13=5087
对应每个染色体Ci的选择概率pi如下:
p1=0.089269,p2=0.110783,p3=0.089269,
p4=0.089269,p5=0.089269,p6=0.110783,
p7=0.110630,p8=0.110630,p9=0.089269,
p10=0.110829
对应每个染色体Ci的累计概率gi如下:
g1=p1=0.089269,g2=p1+p2=0.200052,g3=0.289321,g4=0.378590,g5=0.467859,g6=0.578642,g7=0.689272,g8=0.799902,g9=0.889171,g10=1.000000
假设10次生成的[0,1]间的随机数如下:
0.181431 ,0.322062,0.766503,0.881893,0.650871,0.582475,0.177618,0.343242,0.032685,0.197577
第一个随机数大于g1,小于g2,这样染色体C2被选中,依次类推,产生新的种群由下列染色体组成:C2、C4、C8、C9、C7、C7、C2、C4、C1、C2。
6)交换与变异操作
假设交换概率为0.2,可算出有两个染色体需要交换操作,增加算法个体自学习过程,选出排在前面适应度最差的是C4=111001、C9=111101进行交换,假设取上面第一个随机数,则在第二位进行交换,由于基因都是“1”,则交换前后没有发生改变。C'4=111001=C4、C'9=111101=C9。
假设变异概率0.01,可算出有一个基因需要变异。增加算法个体自学习过程,除去进行交换的C4、C9后继续选出排在前面适应度最差的仍然是C4=111001,变异基因的位置也是随机确定的,假设取上面第一个随机数,则在第二位进行突变,变成C″4=101001,可算出 f(C″4)=15,相对之前的∞ (取值1000),适应度提高不少。为了提高遗传算法的收敛速度,改善算法效率,需要比较变异前后染色体的适应度,若适应度提高则保留,反之则去除或者重新变异一次。至此,完成第二代群体。
通过比较可以看出,第二代群体比第一代群体(即初始群体)的适应度明显提高。由于在交换和变异中增加个体学习,有效避免了交换与变异的风险,提高算法的收敛速度,但是却影响了算法的多样性。继续转向第四步:适应度计算(个体评价),反复迭代直至满足终止条件。
使遗传算法终止的方法主要有二种:
1)规定最大迭代数N。一旦遗传算法的迭代次数达到N,则停止操作,输出结果。通常N取100~1000次。随着计算机速度提高,此方法最常用。
2)记录适应度的变化趋势。在算法初期,群体的平均适应度较小,随着复制、交叉、变异等操作,适应度值增加。如果这种增加已趋缓和或停止,即终止遗传算法。一般如果连续10次适应度没有增加,则停止。
3 算法结果分析
由于群体数量少,路网节点简单,运行速度快,算法采用第一种终止方式,算法执行1000代,最优个体为101010,不及第89代最优个体100100和第263代的最优个体100101、100100。
通过算法实现,适应度比较高的个体有:100100、100101、010010、101010。对应路径分别为
100100:{U0、U1、U4、U7};
100101:{U0、U1、U4、U6、U7}
010010:{U0、U2、U5、U7}
101010:{U0、U1、U3、U5、U7}
交换概率、变异概率、群体数量都是比较重要参数,需要根据具体问题进行适当调整。
最后需要进行两点说明:一是如果要考虑油料保障行进速度、行进安全性等问题,属于多目标优化问题,解决的思路是先用多目标优化方法,如模糊层次分析法,进行无量纲处理,转化为最短路问题[3]。不属于本文研究范围,在此不再赘述。二是油料保障路径优化时,由于最优路径(含次优路径)大大少于路网数量,经历的节点远小于路网节点,用传统遗传算法进行编码、选择、交叉操作,很可能将大量运算浪费在处理无效数据上,在运算过程中也会产生较多的无效解,因此需要在算法的编码、交叉等操作方面加以改进。
[1]熊伟,张仁平,刘奇韬,等.A*算法及其在地理信息系统中的应用[J].计算机系统应用,2007,(4):14.
[2]雷英杰,张善文,李续武,等.MATLAB遗传算法工具箱及应用[M].西安电子科技大学出版社,2005:8.
[3]张仁平,许红,熊伟.不同含权方式物资输送路径优化模型研究[J].中国储运,2009,(4):95.

