一种改进的组织发现算法研究

王 艳， 熊淑华， 梁 云

（①四川大学 电子信息学院，四川 成都 610064；②西南电子电信技术研究所，四川 成都 610041）

0 引言

现实世界中包含着各种类型的复杂网络[1]，例如，科技文献引用关系网络、社会关系网络等。通常人们采用关系网络图的方式对网络中的各种关系进行描述。关系网络图由一组点和线构成，点代表网络中存在的各种实体，线则代表实体与实体之间的相互作用、社会关系等。寻找和发现复杂网络中的组织，有助于更加有效地理解和掌握网络的结构和功能[2]。

Girvan和Newman把Freeman[3]提出的点介数（Vertex Betweenness）由点推广到了边，提出了基于边介数（Edge Betweenness）的组织发现算法[4]，文中称之为Betweenness算法。一条边的边介数表示任意两节点对之间最短路径中，有几条路径经过了该边。Girvan和Newman发现组织与组织之间边的边介数远远高于组织内部边的边介数，依据这一点，Betweenness算法通过逐步移走边介数最大的边来实现组织发现。Betweenness算法简单易懂，但是却存在两点不足：①计算速度慢。Girvan和Newman在文献[5]中指出，最简情形下Betweenness算法的计算复杂度为O( m2n)，其中m、n分别为网络中的边数和顶点数；②由于Betweenness算法并不能明确指出组织发现过程应当在何时结束，这就需要事先知道网络中的组织总数。然而，在发现所有组织之前确定网络包含的组织总数是很难的，这就进一步限制了Betweenness算法的适用范围。

Ulrik Brandes提出了一种Betweenness的快速算法[6]，文中称之为Brandes算法。Brandes算法的基本思想是：任选一个顶点为中心，找到该点到图中其他顶点的最短路径，根据这些最短路径来计算每条边的边介数，然后改变中心点，再重复这个过程，直到每个顶点都被选做中心一次为止，这样对每条边的边介数都计算了两次。Brandes的计算复杂度为O( nm+n2lnn)。

Dennis M. Wilkinson和Bernardo A. Huberman提出了一种组织发现算法[7]，文中称之为Wilkinson-Huberman算法。Wilkinson-Huberman算法在计算边介数时对Brandes算法进行了改进，它不是将每个顶点都作为中心，而是循环的随机选取至少n（n=10lnN-25，其中N为网络中的顶点数，对于特别大的N，n取40就足够了）个点作为中心，计算从这些点出发的每条边的边介数，然后移除边介数最大的那条边，最后将每次循环产生的组织进行整合，得到最终的结果。Wilkinson-Huberman算法在计算复杂度上优于Brandes算法，但由于只是随机选取了n个点作为中心，计算每条边的边介数，因此在准确度上有所损失。

鉴于Betweenness算法和Wilkinson-Huberman算法在复杂度和准确度上存在的局限性，文中对Wilkinson-Huberman算法进行了优化，通过计算互信息[8]（MI），对之前形成的组织进行扩展，最大限度的发现组织的所有成员，称这种新的组织发现算法为 WH-MI算法。该算法计算复杂度低，无需事先知道网络中的组织总数，并且能够发现已知组织的隐藏成员和确定未知组织的完整结构，因此该算法具有更广阔的应用前景。

1 算法原理

首先，把数据记录表示成关系网络图的形式。

接着，使用Wilkinson-Huberman算法对前面形成的关系网络图进行组织发现。首先循环的随机选取50个点[7]为中心，计算所有边的边介数，然后移去边介数最高的边，将关系网络图分割成更小的连通子图，接着反复进行这个过程，直到满足停止条件为止，这样将得到多个满足停止条件的连通子图。对于这些满足停止条件的连通子图称为群体。所有这些群体的集合称为一个结构。由于重复了50次，将得到50个结构。最后整合所有结构中的群体，得到要找的种子组织。

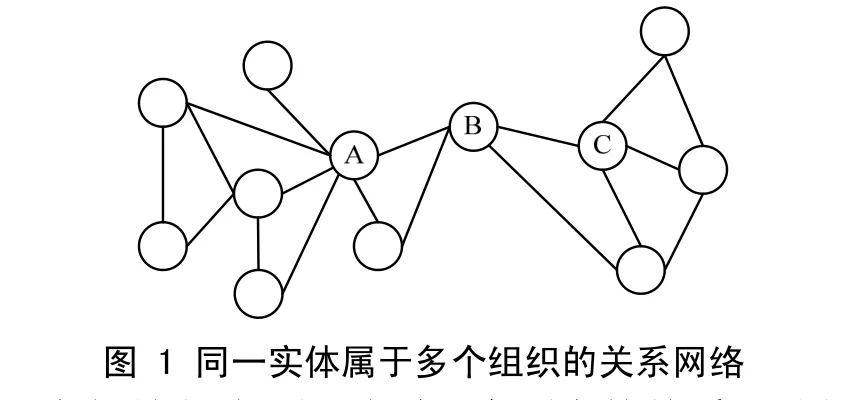
然而实际数据中常常有一个实体属于多个组织的情况，如图1所示，包含了2个组织[9]，左边的组织包含点A，右边的组织包含点C。在图1中的所有连线中，AB和BC都具有很高的边介数。如果先移除连线BC，那么AB就会因为具有较低的边介数不会被移除，点B就会被划分到左边的组织中。而如果先移除连线AB，那么同样的BC也会因为具有较低的边介数不会被移除，点B就会被划分到右边的组织中。因此需要找到一种方法解决一个实体属于多个组织的情况。众所周知，互信息能够用于描述两个随机变量之间的相互依赖性，即如果它们彼此独立，则它们之间的互信息为0；如果它们互相依赖很紧密，则互信息就会很大。于是，在使用Wilkinson-Huberman算法得到种子组织集合G{G1,G2,…,Gn}之后，对G中的每一个子组织Gi(i=1,2,…,n)和在原始的关系网络图中与Gi存在联系的一级联系人建立互信息模型，分别计算这些联系人与Gi内每个成员的互信息值，当所有互信息的平均值超过预先指定的阈值β时，就将这个点加入到子组织Gi中。通过这个过程，就能够较好地解决同一实体属于多个组织的情况。关于阈值β的选取，通常是针对不同类型的数据集，采用实验法来确定的[8]。

综上所述，假设对包含N个顶点的关系图进行组织发现，WH-MI算法的步骤如下所示：

1）进行50次[7]迭代。

2）检测关系图是否包含多个连通子图。

3）对每个连通子图，检查其是否满足停止条件：

如果连通子图满足停止条件，把它从关系图中移出。

如果不满足，则计算连通子图内每条边的边介数，然后移去具有最大边介数的边，直到连通子图被分成两个更小的连通子图。

4）重复步骤3)，直到所有的实体从关系图中全部移出，这时形成了1个组织集合Si。

5）对步骤1)～4)之后形成的50个组织集合中的组织进行重新整合，形成1个组织集合G。

6）通过计算互信息，对G进行扩充。

从算法的步骤中可以看出，步骤1)～5)是Wilkinson-Huberman算法，WH-MI算法是在Wilkinson-Huberman算法的基础上，结合互信息进行组织成员的扩展。因此，与Wilkinson-Huberman算法相比，WH-MI算法得到的组织成员更为完整。

Wilkinson-Huberman算法的基本原理可以参考相关文献[7、9]深入了解。下面将详细阐述利用互信息扩展隐藏组织成员的过程和原理。

在得到种子组织之后，尝试通过查找与一个或多个种子成员有着密切联系的实体，来确定种子组织的附加成员。为了找到这些与种子组织具有密切联系的实体，就需要统计它们与种子组织中的已知成员之间的联系程度，这就需要通过建立互信息模型来实现。

以电话通信为例，知道两个电话号码之间的通话行为具有不确定性，也就是说可以把两个电话号码的一次通话看作一个随机事件，显然该随机事件的结果只有2个，要么是这两个电话号码之间有通话，要么是没有通话。如果用一个两维随机变量(X,Y)的取值来表示该随机事件，则该随机变量的定义域为{P，φ}，其中P代表随机变量X与Y有通话行为，φ表示没有发生通话行为。因此，两个电话号码之间的关联度就可以用其相应的随机变量的互信息来度量。从信息论的角度来看，一次通话的过程其实也是传递信息的过程，通过传递信息来消除通话行为的不确定性，因此，两个随机变量的互信息可以解释为知道一个随机变量的取值后对另一个随机变量的不确定性的减少量，或者一个随机变量包含的另一个随机变量的信息量。根据经典的信息论[10]，定义两个随机变量X和Y的互信息如下：

式中，P(x)=Prob(X=x),P(y)=Prob(Y=y)。

所以，对种子组织进行成员扩展的过程如下所示：

1）对于种子组织中的每一个成员，在原始关系网络图中找到与之有联系的实体，并将它们添加到种子组织中，形成一个新的群体。这样就得到了一个扩展的组织。

2）将扩展后的组织看作是一个整体，计算所有新增实体与种子组织中各成员之间的互信息值。

3）计算每一个新增实体与种子成员中所有成员互信息值的平均值，当这个平均值高于预先指定的阈值β时，则保留这个实体，否则将实体从扩展组织中删去。

4）对步骤3)得到的扩展后的组织，再重复一次组织扩展的过程。

为了便于理解，借助图2、表1和表2来说明建立互信息模型的过程。假设得到的实体关系图如图2所示，统计各实体之间发生的事件如表1所示，计算得到各实体之间的互信息如表2所示。

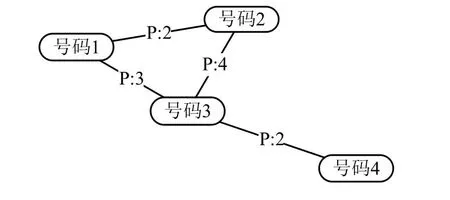
图2 实体关系

表1 各实体之间发生的事件表

表 2 各实体之间的互信息

2 实验结果分析

现将使用网络分析领域中的经典数据集“空手道俱乐部网络（Karate Club Network）数据” 和“大学生足球联赛网络（College Football Network）数据”，对WH-MI算法进行可靠性验证。

2.1 空手道俱乐部网络数据实验

空手道俱乐部网络数据是社会网络分析领域中的经典数据集，由社会学家 Zachary耗时两年观察美国一所大学中空手道俱乐部 34名成员间的社会关系而得到的。由于俱乐部的管理者和老师之间就是否提高俱乐部的费用发生了争论，结果俱乐部分成了两个分别以管理者和老师为中心的俱乐部。图3中，圆形顶点和方形顶点分别代表俱乐部分开后形成的两个新俱乐部的成员。

图 3 Karate Club Network数据示意

利用 WH-MI算法对空手道俱乐部网络数据进行组织发现，得到两个组织，两个组织包含的成员如表3所示。

表 3 Karate Club Network数据实验结果

将表3与图4对比后发现，使用WH-MI算法发现的两个组织结构完全正确。

2.2 大学生足球联赛网络数据实验

大学生足球联赛网络数据模型是Newman等人对美国大学生足球联赛情况分析整理而建立的一个复杂网络模型。参加足球联赛的有若干支球队，网络的每个节点分别代表一支球队，2个节点之间的边代表2 支球队之间进行过一场比赛。联赛中存在若干的联盟，每个球队都属于其中一个联盟。该模型中存在115支球队（个节点）及616场比赛（条边），包含了12个联盟。

使用WH-MI算法进行联盟划分，得到11个组织。组织结构如表4所示。

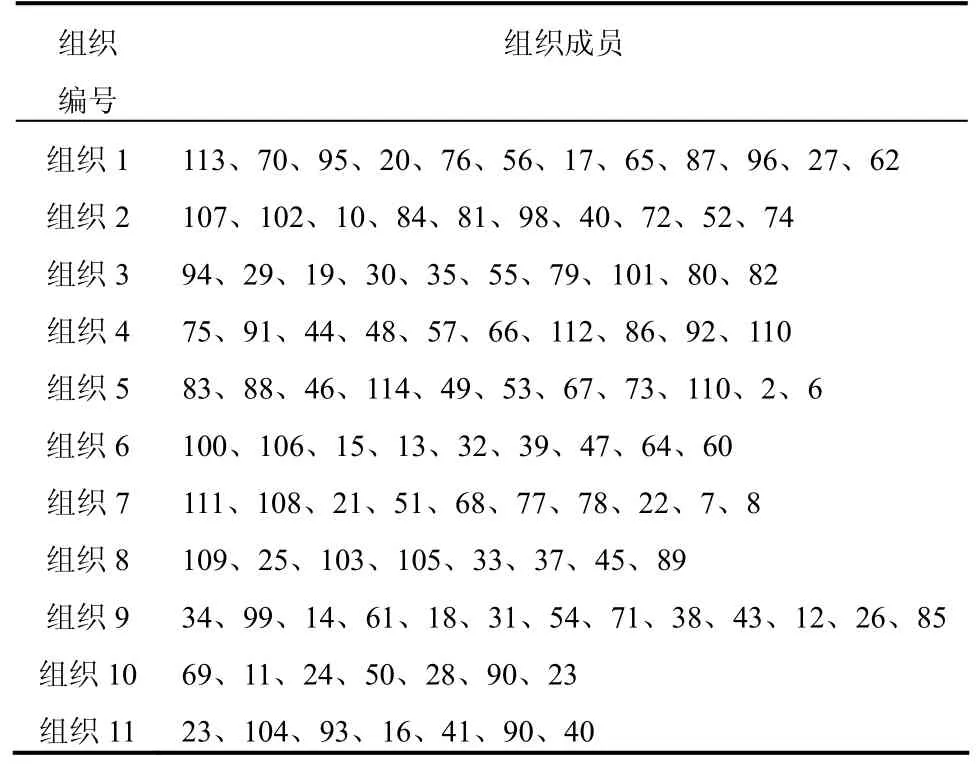
表4 WH-MI算法划分结果

使用Wilkinson-Huberman算法进行联盟划分，得到11个组织。组织结构如表5所示。

表5 Wilkinson-Huberman算法划分结果

对比表4与实际情况发现，划分正确的节点为99个，正确率约为86%。对比表5与实际情况发现，划分正确的节点为97个，正确率约为84.3%。由此可见，使用 WH-MI算法进行组织发现的准确率，比使用Wilkinson-Huberman算法进行组织发现的准确率高。

3 结语

文中分析了经典的Betweenness算法和Wilkinson-Huberman算法，针对Betweenness算法在组织发现方面的不足，结合Wilkinson-Huberman算法以及互信息技术，提出了一种新的组织发现算法(WH-MI算法)。与目前其他一些划分算法相比，该方法不必事先知道网络中的组织总数；同时，由于使用了互信息技术对形成的组织成员进行扩展，得到的组织结构更为完整。最后采用空手道俱乐部网络数据和大学生足球联赛网络数据对算法进行了实验验证，实验结果与实际的划分基本吻合，说明该算法是可行的。

[1] 陈文华,蔡皖东,赵煜.基于数据挖掘的匿名通信关系分析模型研究[J].信息安全与通信保密,2008(06):51-52.

[2] 孙义明,曾继东.数据挖掘技术及其应用[J].信息安全与通信保密,2007(08):80-82.

[3] FREEMAN L C. Centrality in Social Networks:Conceptual Clarification[J].Social Networks,1979(01):215-239.

[4] GIRVAN M, NEWMAN M E J. Community Structure in Social and Biological Networks[J]. PNAS,2002,99(12):7821-7826.

[5] NEWMAN M E J, GIRVAN M. Finding and Evaluating Community Structure in Networks[J]. Physical Review E, 2004, 69(02):26113-26128.

[6] BRANDES U. A Faster Algorithm for Betweenness Centrality[J]. Journal of Mathematical Sociology,2001, 25(02):163-177.

[7] WILKINSON D, HUBERMAN H. A Method for Finding Communities of Related Genes[J]. PNAS,2004(101):5241-5248.

[8] ADIBI J, CHALUPSKY H, MELZ E, et al. The KOJAK Group Finder: Connecting the Dots via Integrated Knowledge-based and Statistical Reasoning[C]// In Proceedings of the Sixteenth Innovative Applications of Artificial Intelligence Conference (IAAI-04).California: San Jose, 2004: 800-807.

[9] TYLER J R, WILKINSON D M, HUBERMAN B A. Email as Spectroscopy: Automated Discovery of Community Structure within Organizations[R]. The Netherlands:Hewlett-Packard Labs, 2003.

[10] SHANNON C.A Mathematical Theory of Communication[J].Bell System Tech,1948(27): 379-423.