微积分中值定理“中间点”渐进性的统一
杜争光
(陇南师范高等专科学校 数学系,成县742500)
1 主要引理
在微分中值定理和积分中值定理中,“中间点”渐进性的研究,引起了广大数学工作者的广泛兴趣和积极研究,并取得了一些重要结果(见文献[1]-[8]).
文献[1]对微分中值定理和积分中值定理进行了统一和推广,本文讨论统一后的微积分中值定理“中间点”的渐进性,并对已有的“中间点”渐进性结果进行统一和推广.
为叙述和讨论方便,现将统一后的微积分中值定理及文中需要的一些中值定理引述如下:
引理1[1]若函数f(x)和g(x)在a的某一邻域U(a)内满足条件:
(1)n阶导数连续;
(2)n+1阶导数存在;
(3)∀x∈U(a),g(n+1)(x)≠0.
则对∀b∈U0(a),至少存在一点ξ在a与b之间,使得

(Cauchy中值定理)若函数f(x)和g(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,且∀x∈(a,b),g′(x)≠0.则至少存在一点ξ∈(a,b),使得

(积分型Cauchy中值定理)若函数f(x)和g(x)满足在闭区间[a,b]上连续,且 ∀x∈ (a,b),g(x)≠0.则至少存在一点ξ∈ (a,b),使得(Lagrange中值定理)若函数f(x)满足下列条件:

(1)在闭区间[a,b]连续;
(2)在开区间(a,b)可导.
(Taylor中值定理)若函数f(x)在a的某一邻域U(a)内存在n+1阶导数,则∀x∈(a),在a与x之间至少存在一点ξ,使
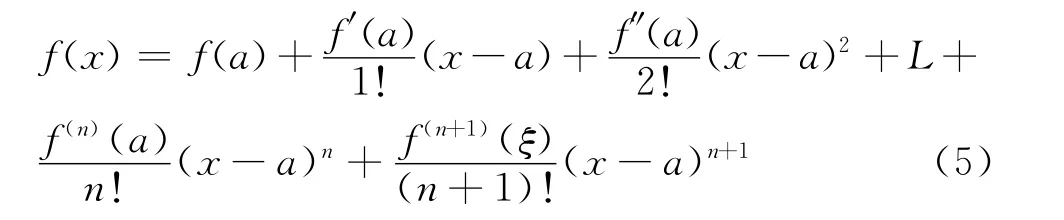
(积分第一中值定理)若函数f(x)在闭区间[a,b]上连续,则至少存在一点ξ∈ [a,b],使得

(推广的积分第一中值定理)若函数f(x)在闭区间[a,b]上连续,g(x)在闭区间[a,b]上可积,且不变 号,则 至 少 存 在 一 点 ξ ∈ [a,b],使 得

(积分第二中值定理)设函数g(x)在[a,b]可积,函数f(x)单调,且f(x)≥0,则 ∃η∈ [a,b],使得

2 主要结果





即(2)式成立,同理可证(3)式成立.

,ξ是由(1)式所确定的“中间点”,则



基于以上的定理,就有以下的推论:

证明 在(11)式中,令β=0,m =1即得.

证明 在(11)中,令β=0,m =1即得.

证明 在(11)中,令m =1即得.

证明 在(11)式中,令β=0,m =1,α =n即得.

证明 在(11)式中,令β=0,α=p ,m=n即得.

证明 在(11)中,令m=1,β=0即得.

证明 在(11)中,令m=0,β=p+1,α=p+q+1即得.
推论8[8],[9]设函数f(t)在[a,x]可导,单调,且f(t)不是常数,g(t)在[a,x]连续且不变号,η是由积分第二中值定理(8)所确定的“中间点”,则

证明 在(11)中,令m=1,β=0,α=1即得(1),令m=n,β=0,α=1即得(2).
从以上的推论可以看出,(11)式不仅将微分中值定理和积分中值定理“中间点”的渐进性进行了很好的统一,而且将微分中值定理和积分中值定理“中间点”的渐进性已有的结果进行了推广.
[1] 杜争光.微积分中值定理的统一与推广[J].荆楚理工学院学报,2011,26(2):34-36.
[2] 程希旺.微分中值定理中值点渐进性研究的新进展[J].数学的实践与认识,2010,39(14):229-233.
[3] 刘文武,严中权.积分型Cauchy中值定理中间点的渐进性[J].数学的实 践与认识,2010,40(11):228-231..
[4] 戴立辉.微积分中值定理的变化趋势[J].工科数学,1994,10(4):178-181.
[5] 孙千高.Taylor展开式在“中值点”渐进性中的应用[J].宝鸡文理学院学报,2005,25(3):176-177.
[6] 张素玲.积分第一中值定理中间点渐进性定理及等价性定理的证明[J].焦作大学学报,2008,(3):60-61.
[7] 宋文青,刘绍庆.积分中值定理的“中值点”渐进性中分析[J].山东师范大学学报,2005,20(1):90-91.
[8] 杜争光.积分第二中值定理“中间点”的分析性质[J].大学数学,2010,26(3):155-160.
[9] 杜争光.积分第二中值定理“中点函数”的解析式[J].湖南工程学院学报,2011,21(4):44-45,62.

