时标上一类中立型动力方程的有界振动解
刘兰初
(湖南工程学院 理学院,湘潭411104)
1 预备知识
自1998年Stefan Hilger[1]在他的博士论文中首次提出时标上的微分方程理论以来,引起了人们广泛的关注,取得了一些好结果,如 Aguwal[2-6]等人的工作.实数R的任意一个非空闭子集称作一个时标,本文以符号T 表示.例如,R、Z、N、[0,1]∪N,都是时标。但有理数集,无理数集,开区间(0,1)等都不是时标。关于时标上一阶中立型动力方程的定性理论的研究还很少,文献[7]考虑了
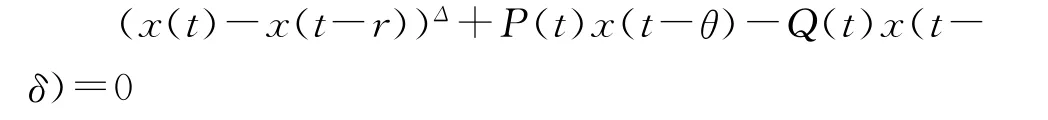
的无界解,文献[8]考虑了

的有界解.上两方程都是在c=1的情形.本文考虑测度链上中立型动力方程:

这里0<c<1,r>0,θ>δ≥0为常数,P,Q∈Crd[T,R+).本文采用如下记号:

2 主要结果
引理1 若H1-H3的假设成立,则方程

与

分别存在有界正解u1(t)和u(t),且

证明:方程(2)与 (3)的证明类似,我们只给出方程(2)的证明.考虑积分方程
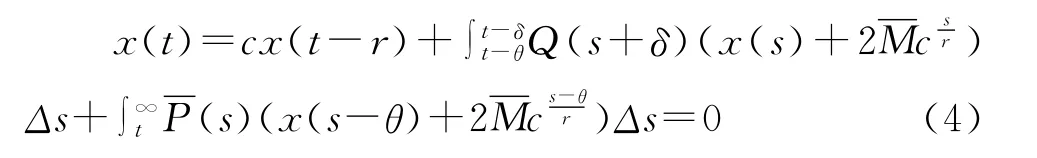

选取t1充分大,使得

很明显 H(t)∈Crd([t1,∞),R+].定义
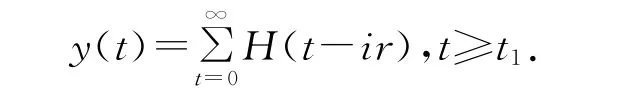


X的算子S,
这里m=max{θ,r}显然,

且

对任意x∈X,有:SX⊂X.

归纳证明得:


那么,可获得:


定理1 假设H1-H3成立,则方程(1)存在一个有界正解.且对任意连续的以r为周期的振动函数ω(t),存在一个有界振动解x(t),使得

这里R(t)为rd-连续的实值函数,且

证明:设
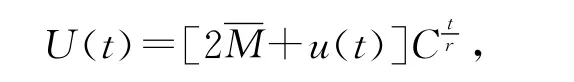

这里u(t),u1(t)由引理2.1定义.由引理2.1知U(t)与U1(t)均为方程(1)的有界正解.由于方程(1)是线性的,故

也为方程(1)的解,且x(t)是(1)的有界振动解,且满足(1).证毕.
推论1 假设H1,H2,H4成立,则定理(2.1)成立.
证明:只须证明H4⇒H3即可.

则

[1] S.Hilger.Analysis on Measure Chains A Unified Approach to Continuous and Discrete Calculus[J].Re-sults in Matematics 1990(18):18-56.
[2] S.Hilger.Differential and Difference Calculus-Unified[J].Nonlinear Analysis,1997,30(5):2683-2694.
[3] M.Bohner,A.Peterson.Dynamic Equations on time scales[M].Boston:Birkhauser,2001.
[4] R.P.Agarwal,M.Bohner.Basic Calculus on Time scales and Some of its Applications[J].Results Math.,1999,35:3-22.
[5] M.Bohner,J.E.Castillo,Mimetic Methods on Measure Chains[J].Comput.Math.Appl.,2001,42:705-710.
[6] L.Erbe and A.Peterson,Riccati Equations on a Measure chain,In Proc[M].Dynamic Systems Appl.,Volume 3,Dynamic Publishers,2001:193-199.
[7] 刘兰初,龙玉花.测度链上一阶中立型动力方程的无界解[J].湖南工程学院学报(自科版),2006(4).
[8] 刘兰初,刘光辉 .测度链上具有正负系数的中立型动力方程的有界解[J].江西师范大学学报,2006(4).

