非线性反应扩散问题两网格混合有限元法的数值分析

杨继明，李 熙

（湖南工程学院 理学院，湘潭411104）

0 引 言

反应扩散方程在实际生产和科研中有许多应用，水文、物理、化学、生物学和人口动力学中众多的数学模型就是反应扩散方程，这类方程描述了水污染、地下水渗流、污染物迁移等诸多现象，所以研究这类方程的数值解法具有重要的现实意义.在许多情况下，不但需要求出函数值，而且其导数值也是很重要的量，需要尽量提高离散解精度，所以人们往往选择用混合有限元方法来求解此类问题，并做了一些理论研究.但由于这类问题离散后得到的非线性系统求解比较困难，需要采用高效的数值算法.两重网格算法就是其中的一种.

文献［1］最先提出两重网格算法（1949年），求出非线性问题在粗网格上的解以后，再利用Taylor展式将粗网格上的解外推到细网格上去.文献［2］将两重网格算法结合特征线法用于求解对流占优的对流扩散问题，极大地提高了计算效率.陈艳萍教授［3－4］等对一类非线性反应扩散问题给出了混合有限元方法的两重网格算法.但关于两重网格算法数值实现的文献较少.本文将两重网格算法用于一类更复杂的非线性反应扩散方程，构造两网格混合有限元算法并从数值角度进行分析.

1 混合有限元法

考虑渗流力学中的下列非线性反应扩散问题

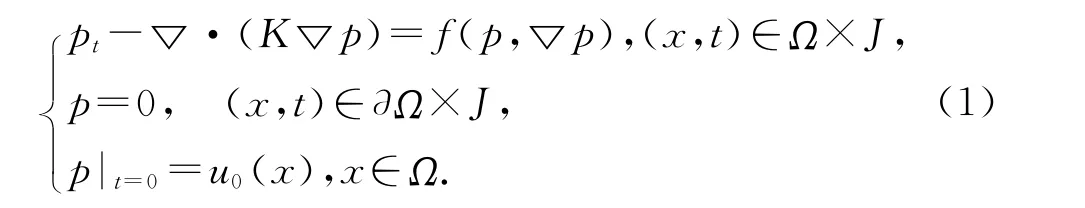
其中Ω⊂R2为有界凸区域，pt＝∂P／∂t，J＝（0，T］.K为对称的一致正定张量，即存在两个正常数K＊和K＊使得对于任意的z∈R2，有K＊‖z‖2≤zTK（x）z≤K＊‖z‖2，x∈Ω.p未知，f为已知的二次连续可微函数.

采用混合有限元方法进行离散.

设L2（Ω）为Ω 中平方可积函数的集合，（L2（Ω））2为每个分量在L2（Ω）中的二维向量函数空间，H（Ω，div）为（L2（Ω））2中散度仍在L2（Ω）中的向量空间.设V＝H（Ω，div），W＝L2（Ω）.记Vh和Wh分别为V和W 的离散子空间.Vh和Wh分别采用标准的混合有限元空间即k阶的RT空间［5］或k阶的Brezzi－Douglas－Marni空间（BDM）［6］.

设置变量u＝－K2p，则问题（1）的解（p，u）∈W×V即为下列变分问题的解：

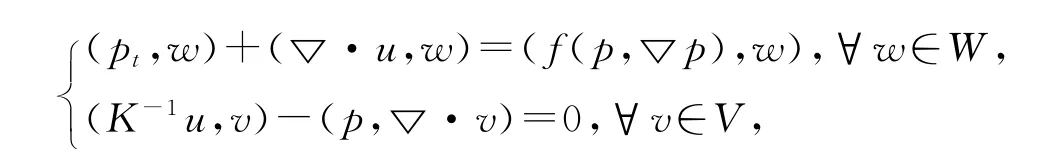
令

在t＝tn时刻，（2）可以改写为：

于是，离散时间的混合有限元格式为：寻找（pnh，unh）∈Wh×Vh使得

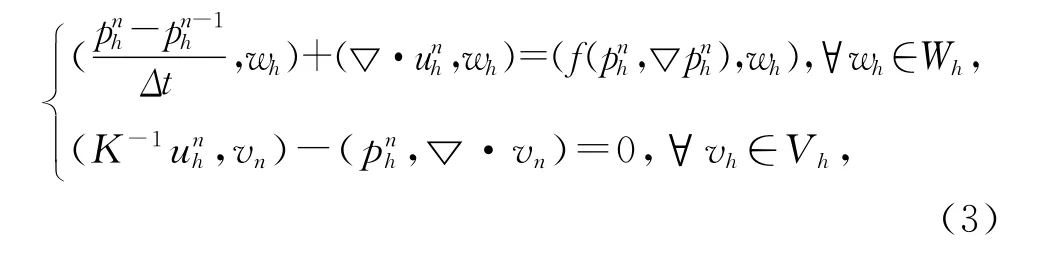
2 两网格混合有限元算法

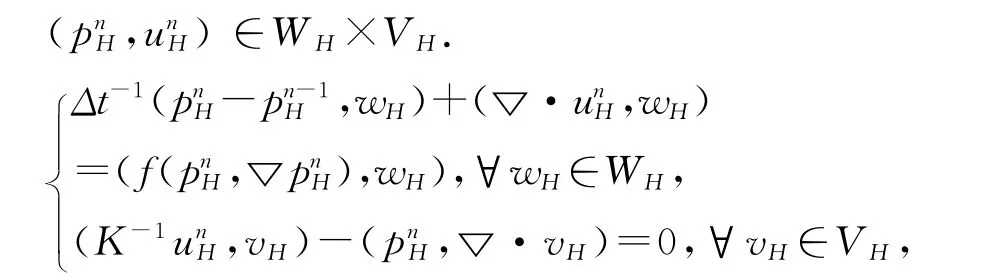
非线性系统（3）一般采用牛顿迭代法求解，在每一个时间层上都需要进行若干次迭代运算.我们采用两重网格算法.

设Vh×Wh和VH×WH⊂Vh×Wh为网格尺寸分别为h和H（h＜H＜1）的拟一致网格剖分上的混合有限元空间.

给出如下的两网格混合有限元算法.首先在粗网格上求解非线性方程组，然后在细网格上执行一次牛顿迭代，求解的是线性代数系统.

第一步：在粗网格上求解非线性系统求得解

3 数值实验分析

考虑下面的非线性反应扩散问题：

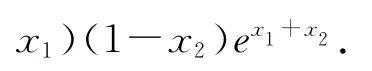
表1 两网格混合有限元方法的误差和计算时间

表2 混合有限元方法的误差和计算时间

从以上数据可以看出，为了达到相同的精度阶数，两网格混合有限元方法比单纯的混合有限元方法计算的速度更快，效率更高.

对于非线性反应扩散问题，混合有限元法离散后的代数系统，需要采用比较耗时的非线性迭代运算求解.两网格算法引入后，我们只要在粗网格上进行非线性迭代，在所需求解的细网格上进行的只是线性运算，这样便节约了大量计算时间，使计算效率大大提高.

［1］ Xu J.A Novel Two Grid Method for Semilinear Elliptic equations［J］.SIAM J Sci Comp，1994，15：231－237.

［2］ Qin X Q.Two Grid Method for Characteristics Finite Element Solution of 2DNonlinear Convection Dominated Diffusion Problem［J］.Applied Mathematics and－Mechanics，2005，26（11）：1506－1514.

［3］ Chen Y P，Liu H W，Liu S.Analysis of Two－Grid Methods for Reaction－Diffusion Equations by Expanded Mixed Finite Element Methods［J］.Int J Numer Meth Engng，2007，69：408－422.

［4］ Chen L，Chen Y P.Two－Grid Method for Nonlinear Reaction－Diffusion Equations by Mixed Finite Element Methods［J］.J Sci Comp，2011，49（3）：383－401.

［5］ Raviart PA，Thomas TM.A Mixed Finite Element Method for Second Order Elliptic Problems［M］.In Mathematical Aspects of FEM，Lecture Notes in Mathematics，Springer：Berlin，1977，292－315.

［6］ Brezzi F，Douglas Jr J，Marini LD.Two Families of Mixed Finite Elements for Second Order Elliptic Problem［J］.Numerische Mathematik，1985，47：217－235.