泛在网络中的等效频谱带宽概念及其在异构网络切换中的应用

潘甦，叶强，刘胜美

（1.南京邮电大学 无线通信江苏省重点实验室，江苏 南京 210003；2.东南大学 移动通信国家重点实验室，江苏 南京 210096）

1 引言

未来网络在网络层实现全 IP化的趋势已经非常明显，而在网络层以下，没有一种技术可以在任何条件下满足用户的所有需求，所以，众多的无线接入网以异构并存的方式共同发展，不存在统一的趋势。因此，异构网络融合是未来泛在网络的基本特征之一，也是移动泛在业务环境(MUSE)的核心思想[1,2]。

泛在网络在技术上追求的是无线资源效率和业务QoS间的最佳平衡，因此，无线资源管理是其研究热点之一。众多无线接入网多址方式不同，使得其无线资源颗粒（资源单位）具有完全不一样的表现特征。如采用 TDMA 的系统有完备的资源单位—“时隙”，而CDMA系统的用户采用扩频方式占用全部带宽，因此，对于用户来说没有完备的资源颗粒，系统的无线资源以码道、功率、误码率容限等各自表达资源的某个特性。对于特定用户而言，统计时分多址的WLAN更没有直接的资源单位，因此，异构的无线资源缺乏统一的、可比较的资源度量。

在泛在无线资源管理中，无论是网络选择还是移动性管理的相关算法，由于缺乏网络间统一的资源颗粒，很多算法是多目标(QoS本来就是多指标)、多约束条件（资源表征不完整，每个表征造成一个约束，如功率约束等）情况下的优化问题，这在多数情况下无法得到最优解，采用各种迭代方法逼近次优解的算法也相当复杂。比如在目前的异构网络垂直切换研究中，一般把垂直切换看作一个多约束条件下的决策问题。文献[3～5]为切换决策要涉及的每种因素分配了相应的权值，选择加权和最大的网络为切换的目标网络。文献[3,6]对一些难以量化的参数采用基于模糊推理的方法进行决策，首先把模糊数据转换成一个实数，然后使用经典的模糊多参数决策方法（MADM方法），即采用模糊逻辑的方式来表示某些网络参数及用户偏好，以决定候选网络的优先级。

为了解决异构网络的资源统一量化，本文为泛在异构无线网络提出了等效频谱的概念。尽管无线资源根据不同的划分方式在不同的系统中有不同的表达,然而因为传输媒质都是统一的电磁波。因此，上述资源只是电磁频谱在不同正交空间中分割时的表达，本质上都可以映射为对等效频谱的占用。由于引入了等效频谱概念，以获得频谱的多少为主要参数为切换呼叫定义服务质量的收益函数，从而可以将马尔可夫决策模型引入垂直切换过程，目标是使每个呼叫在持续期内总收益最大。

2 等效频谱概念

频分多址系统中，系统在频率空间中通过切割频谱以容纳多用户，用户占用的无线资源可以直接表示为一段频谱。而CDMA或WLAN等非频分系统在码分和统计时分空间中容纳用户，因此等效频谱定义为非频率空间中用户占用的资源在频谱空间上的映射。

2.1 CDMA网络中用户占用的等效频谱

首先，考虑多业务多码道CDMA系统[7]，各种业务用Φm表示，m=1,…,M。对于业务Φm，用户产生的数据分组首先被分解成Cm个平行发送的子分组，这些子分组通过不同的正交扩频码扩频并被同时传送。

用广义静态非相关散射信道(WSSUS)作为频率选择性Rician衰落多径信道的模型[8]，mΦ业务类的信号噪声干扰比表示为[7,9]

其中，Pm是Φm业务类呼叫在基站端每码道的接收功率，G是扩频增益，Nm是Φm业务类中呼叫的个数，F(G)取决于WSSUS信道中和衰减过程相关的协方差函数，在文献[9]中有其定义；参数v是衰落信道的传输系数，N0是高斯噪声的谱密度，Ebm是每信息比特能量,它可以表示为Ebm=Pm/B。假设Rm是Φm业务所需的最小信号噪声干扰比，有：

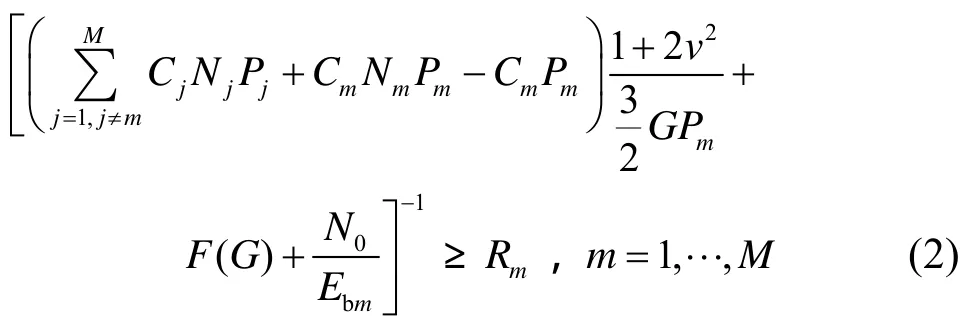
式(2)实际上是一个不等式组,该不等式组表明，在CDMA系统中,要使得同时发送的属于不同业务的数据分组在接收端具有不同的误码率,必须使得这些数据分组在接受端有不同的接受功率电平{P1, P2,…,PM}。该功率电平的存在条件和用户数和系统带宽有联系，根据该条件可以将用户占用的资源映射成等效带宽。

定义

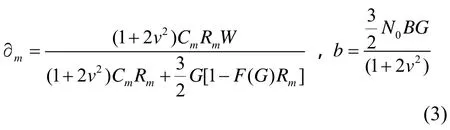
将式(3)代入式(2)，经过代数运算可得最小的Pm是[10]

从式(4)的分母可见，功率解Pm存在的充要条件是，即

从式(3)关于m∂的定义中可见m∂是以误码率要求mR加权的发送比特率（mC代表发送比特率）。它可以被认为是一个处于激活状态的呼叫所占据的频谱带宽的加权值，即为等效带宽，同理,所有的呼叫占据的等效带宽就是。因为系统总的带宽是W，很明显，不等式(5)的物理意义在于：系统获得功率解的充要条件是所有呼叫占据的等效带宽必须小于系统所提供的总带宽。这个准则实际上在资源层面上把 CDMA多址方式“转换成”了不同用户占据不同等效带宽的FDMA方式。

2.2 WLAN网络中用户的等效频谱带宽

如同在时分多址(TDMA)中用时隙来表达无线资源一样，在 WLAN系统中，资源是由信道占用时间来表达的。和TDMA不一样的是:一个用户数据分组成功传输所需要的信道时间并不等于数据分组真正传输时占用的信道时间。因为数据分组传输之前要等待信道空闲一段时间，并且传输了也不意味着一定成功，因此通过研究成功传输一个数据分组所需用的时间来着手分析资源，并进而找出它和频谱之间的关系，最终得出等效频谱带宽表达。

考察Φm业务的一个用户，其产生的一个数据分组会经过信道忙闲检测、等待以及可能的多次碰撞一直到成功发送。定义这段时间为“等效占用信道时间”，用mT表示。在这段时间中，网络会有如下情况发生：①网络空闲，该用户处于探测等待时间；②网络忙，其他用户成功发送了数据分组；③网络忙，数据发生碰撞；④网络忙，该用户成功发送数据分组。下面逐一分析各种情况所耗费的时间。

1) 平均等待时间

令Φm类业务的最小竞争窗口为CWm,inm。假设所有的业务类都具有相同的最大重传限制mr。Φm类用户的最大竞争窗为Φm类数据分组在第k次重传时，其竞争窗口大小为

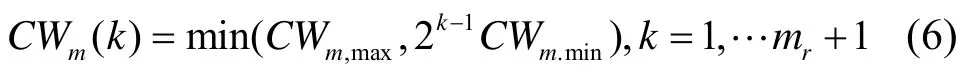
令pm为Φm类用户的数据分组碰撞概率，并且假定不同用户的碰撞概率互不相干。那么用户的平均等待时间用时隙为单位可以表示为

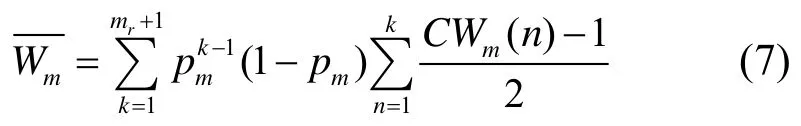
碰撞概率在文献[11]给出：

2）其他用户的平均发送时间

在Tm时间内，除了被考察用户，每个Φm类用户平均产生的数据分组数量为Tmλm（λm为数据分组产生率）。如果系统处于稳定状态，那么在Tm时间内，每个用户产生的数据分组应该在统计上被发送完，每个Φm类用户耗费时间为：λmTmTS，TS为一个数据分组的物理层传输时间，，其中，B为物理层速率，在802.11b中，B为11Mbit/s，它代表了物理层带宽。PS是数据分组的大小（bit/分组），在本文中是个定值。除了被考察用户，整个系统中所有其他用户耗费的总时间为：

3) 平均碰撞时间

在一个数据分组被成功传输之前，它有可能由于冲突而导致失败。对于被考察的一个Φm类用户来说，每成功传输一次所经历的平均失败次数为，因此，在Tm时间内，被考察用户的平均碰撞时间可以表示为

在Tm时间内，系统其他用户因碰撞而占用的时间总和为

基于上述分析，可以得到成功发送一个数据分组的等效占用信道时间为

对于Φm类用户，成功传输一个数据分组的等效占用信道时间为Tm，因此，数据分组传输的等效速率为1/Tm。一个Φm类用户的数据分组产生率为（分组/时隙），为了让WLAN系统稳定，要求即 λmTm＜ 1 。代入Tm的表达式，得：

这要求

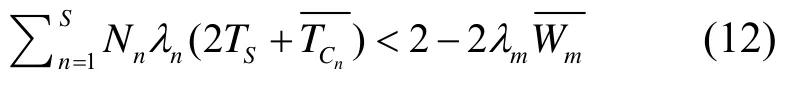
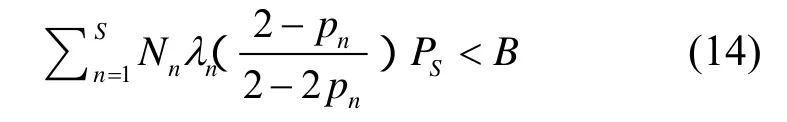
定义βn=为mΦ类业务的等效频谱带宽，上式变为。 明显可见，式子左边是系统中所有用户占用的等效频谱带宽，式子右边的物理层速率代表系统总频谱带宽。因此，式(14)的物理意义和式（5）类似。

2.3 等效频谱概念的推广

从上述推导中可见，“等效频谱”一般的映射方法就是首先利用各种解析方法表达各自空间的资源（如WLAN中的等效占用信道时间）。各个系统虽然有所不同，但这个资源一定可以表达为用户数、用户业务QoS和物理层速率的函数；比如在WLAN中，上述几项分别影响碰撞概率、等待窗口和底层传输时间，因此都对等效占用信道时间这一占用资源作贡献。一定编码和调制方式下物理层速率和频谱的函数关系是确定的，因此接着能把各个资源表达为用户数、用户业务QoS以及频谱的函数。 最后找到系统稳定这个条件对资源的约束，这样就能得到每一个用户在某种业务情况下占用的加权频谱，从而实现各个空间的资源切割到频谱空间的映射。 这种一般方法可以应用在多个系统中，比如应用在 3G长期演进（LTE）系统和WiMAX 所使用的OFDMA系统，该系统中，资源的表达是“时频块”，它是时隙和子载波数构成的二维资源，其传输的速率受用户QoS要求和信道质量影响，因此套用上述一般方法,同样可以将其解析为用户数、用户业务QoS以及频谱的函数，然后根据总载波数的约束，可以得到其在频谱空间的映射。

3 以等效带宽构造状态空间的垂直切换算法

为了使得用户在呼叫持续期内，而不是在切换时刻,获得最大收益,将马尔可夫决策模型(MDP)引入到垂直切换控制中。MDP模型包括5个部分，可以表示为｛T , s, A( s) , p( s′ |s, a ) , r( s, a)｝ 。其中，T是决策周期，A( s)表示在状态s可用的行动集合，行动a∈A( s)，a=1表示选择CDMA网，a=2表示选择 WLAN网。状态转移概率 p( s′|s, a)表示在状态s采取了行动a的条件下，在下一决策时刻系统处于状态s′的概率。

1) 等效带宽和状态空间

状态空间 s=[ i, b1, b2]，其中i表示用户所处的网络，1i=表示 CDMA网，2i=表示WLAN网。b1和b2表示切换用户当前从网络1或网络2分别可以获得的等效带宽 ，它们为该网络总带宽减去网络中原有用户已占用带宽。为简化表述起见，考虑网络中支持2类业务:话音和数据，∂1表示CDMA网络中每个话音用户占用的带宽，∂2是CDMA网络中每个数据用户占用的带宽，β1，β2分别为WLAN网络中每个话音和数据用户所占用的带宽。切换用户在CDMA网络中的可获得带宽在WLAN中的可获得带宽为。由于MDP的状态空间是离散的，因此分别以β1∂1，为基数对b1和b2进行归一化：

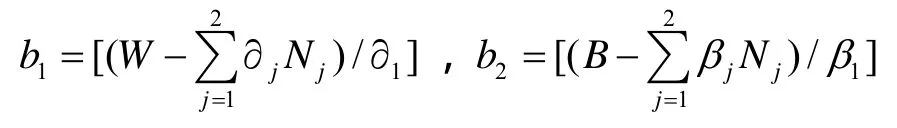
其中，[·]表示取整。

2) 等效带宽和收益函数

收益 r(s,a)表示在状态s采取行为a后，用户得到的链路收益减去信令成本和费用[10]。链路收益反映了用户QoS得到满足的程度，定义为[12]

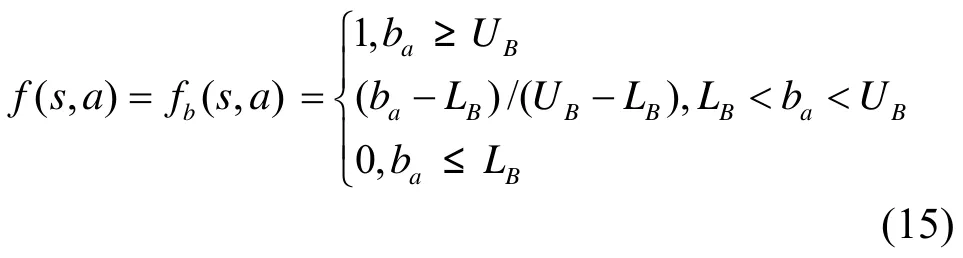
其中，LB和UB分别为用户所需要的最小和最大等效带宽。当可获得等效带宽大于用户所需的最大等效带宽时，收益为 1，带宽的继续增大对满足用户QoS无意义。当可获得带宽介于用户的最小和最大需求时，链路收益随着可获得带宽的增加线性增加；当可获得带宽小于所需最小带宽时收益为0。

定义信令成本函数

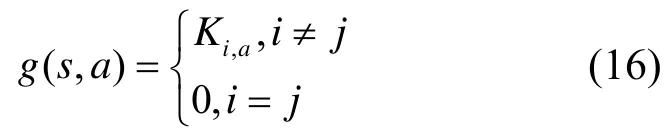
其中，Ki,a为从当前网络i选择行动a切换到网络j的切换成本。

为了使用户更加理性地选择自己的行为，本文采用按占用带宽计费的方式。令Ma表示采取了a行动后所在网络的单位带宽价格，定义网络计费函数为

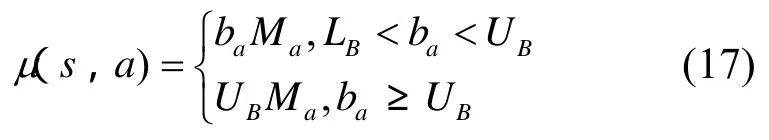
考虑到本文仅针对CDMA和WLAN 2个网络间的切换进行讨论，假设切换信令成本函数k1,2=k2,1=1，则收益函数为

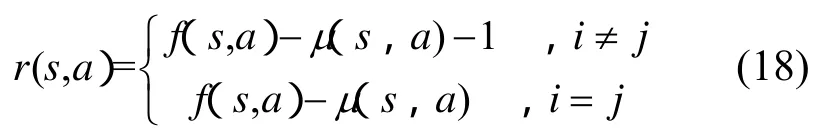
3) 状态转移概率

由于用户只在其状态改变时作切换决策，而状态只有在网络中有呼叫进入或离开时才改变。在实际CDMA系统中，由于呼叫接入请求信道（RACH）采用ALOHA协议，即一个时刻只能处理一个用户的接入请求，所以有理由假设每个决策时刻网络中用户的变化量为1。假设网络中的用户个数服从到达率为λk（k=1，2），离去率为μk（k=1，2）的泊松分布，则当前有n个用户，下一状态有n+1个用户和n-1个用户的概率分别为：Pn+1,n=λe-λ和Pn-1,n=μe-μ，用户数不变的概率为Pn,n=1-λe-λ-μe-μ。

基于上述假设，对于话音用户，其状态转移概率P( s′|s, a)可以表示为

对于数据用户，其状态转移概率只需把上式中的λ1和λ2，μ1和μ2互换即可。

4) 收益最大化算法

令δt为时刻t的决策规则，各个决策时刻上行动原则的集合π=（δ1，δ2，…，δN）称为策略，下标1,…,N是决策时刻。 令vπ（s）为给定初始状态 （s也即t=1时的当前状态s1）从t=1出发使用策略π时的期望总收益，它可以表示为

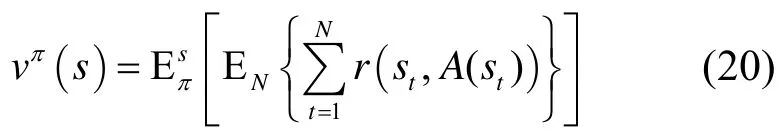
其中，st表示t时刻的当前状态，A( st)表示在st状态下选取的行动，EN为在连接时间N上对总收益求期望，为对给定初始状态s，在选择的策略π上对总收益求期望。假设N是一个几何分布变量，均值为1/1-λ，式(20)可表示成

式(21)实际上可以看成一个离散决策时刻的马氏决策问题，这里的λ又可以理解为折扣因子即折现率。本算法的目的就是要求出使得vπ（s）最大的δ（s），也即一个最优原则的求解问题。本文用值迭代算法来实现这一目标。令v( s)为当前状态为s的期望总收益，即。根据文献[12]，求解式(20)的最大值只需求解下式的最大值：

其中，v(s)是当前状态s和行动a的函数，r(s,a)为在状态s下采取决策a时的收益。

根据文献[12]，算法过程可描述如下。

1) 对∀s∈S，初始化设v0(s)=0，迭代次数k=0，ε＞0。

2)对每个状态s，计算

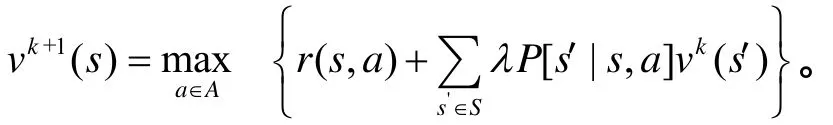
3)如果||vk+1-vk||＜ε(1-λ)/2λ，跳到4），否则令k=k+1，返回2）。

4)这样就可以得到最佳静态策略

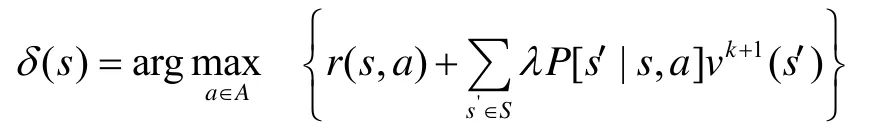
由于步骤 2）相当于一个压缩映射，所以上述VIA算法是线性收敛的[12]。

4 数值结果与仿真分析

仿真系统支持话音和数据2类业务。CDMA网络的小区间干扰因子 f=0.55；衰落信道传输系数v=0.01；扩频增益G=512；话音业务的平行子码数C1=2；最小所需信噪比R1=4.775；数据业务的平行子码数 C2=8；最小所需信噪比R2=6.916；WLAN网络中的数据分组平均产生率分别为话音业务为0.02，数据业务为0.01，折扣因子λ为0.98。 图1给出了不同状态下用户行为以及期望总收益随着带宽价格变化的规律。图1仿真中假定CDMA网络单位带宽价格不变，改变WLAN带宽价格。

图1 WLAN单位带宽价格对期望总收益和行动的影响

从图1中可以看到，随着WLAN单位带宽价格的增加，如果当前用户处于 CDMA网络，它将继续保持行动 1，不发生切换；如果当前用户处于WLAN网络中，随着WLAN价格增加，用户更容易切换到CDMA网络，并且这种可能性随CDMA网络可获得带宽的增加而加大（见状态S的变化），由于收益由可获得带宽、单位带宽价格和切换成本共同决定的，所以不同当前状态下的收益不同，但是在同一状态条件下，随着单位带宽价格增加，整体呈下降趋势。

图 2将本方法和已有的模糊多参数决策方法（MADM方法）[3,6]进行了收益比较。在MADM方法中考虑的参数包括用户占用带宽、价格、电池电量等。由于在CDMA 和WLAN中，用户不是直接以带宽的形式占用资源，MADM 方法不给出带宽和异构网络资源的对应关系，因而事实上仅具有理论意义。同时由于MADM方法未在整个呼叫持续时间进行全局化优化，因此由图2中可见，在各种状态下，本算法都有较大的收益。

图2 期望总收益比较

5 结束语

本文提出了泛在网络等效带宽概念，通过将异构的无线资源统一表达为等效带宽，解决了异构网络资源管理中的资源度量问题，并将其用到垂直切换过程中。这种切换算法考虑了呼叫持续时间内的全局优化，可以给出不同网络的状态下，用户应采取何种行动以得到最大的总收益。仿真结果表明，本算法相比于基于门限的切换法有更大的收益。

[1] NGMN White Paper Version 3.0[R]. 2006.

[2] 张平,纪阳. 移动泛在业务环境及其体系架构设计的挑战[J].北京邮电大学学报, 2005, 28 (5):1-3.ZHANG. P, JI Y. Mobile ubiquitous service environment and the challenges of architecture design [J]. The Journal of Beijing University of Posts and Telecommunications, 2005,28 (5):1-3.

[3] ZHANG W H. Handover decision using fuzzy MADM in heterogeneous networks[A]. IEEE WCNC’04[C]. Atlanta, USA, 2004. 653-658.

[4] ZHU F, MCNAIR J. Optimizations for vertical handoff decision algorithms[A]. IEEE WCNC’04[C]. Atlanta, USA, 2004. 867-872.

[5] CHEN W T, SHU Y Y. Active application oriented vertical handoff in next generation wireless networks[A]. IEEE WCNC’05[C]. New Orleans, USA, 2005. 1383- 1388.

[6] STEVENS-NAVARRO E, WONG V W S. Comparison between vertical handoff decision algorithms for heterogeneous wireless networks [A]. IEEE VTC’06[C]. Melbourne, Australia, 2006. 947-951.

[7] PAN S, TUNG S N, FENG G Z. A novel capacity analyzing method for multimedia CDMA systems based on power on level allocation [J].Journal of Electronics (China), 2006, 23(6): 842-847.

[8] KUN W Y, TUNG S N. Matched filter bound for multipath ricianfading channels[J]. IEEE Trans on Communications, 2002, 4(46):441-445.

[9] BORTH D, PURSLEY M. Analysis of direct-sequence spread- spectrum multiple-access communication over rician fading channels[J]. IEEE Trans on Communications, 2000, 27(1): 1566-1577.

[10] 潘甦, 鄷广增. 等效频谱带宽分配的多媒体 CDMA系统媒质接入控制[J]. 通信学报, 2006, 27(6):126-133.PAN S, FENG G Z. Medium access control of multimedia CDMA systems with effective spectral bandwidth distribution[J]. Journal on Communications, 2006, 27(6): 126-133.

[11] CAI L X, SHEN X M, MARK J W. Voice capacity analysis of WLAN with unbalanced traffic[J]. IEEE Transactions on Vehicular Technology,2006, 55(3): 752-761.

[12] STEVENS-NAVARRO E, LIN Y X, WONG V W S. An MDP-based vertical handoff decision algorithm for heterogeneous wireless networks[J]. IEEE Transactions on Vehicular Technology, 2008, 57(2):1243-1254.