基于空时聚焦传输的多源单中继超宽带网络传输性能分析

田亚飞，杨晨阳

（北京航空航天大学 电子信息工程学院，北京 100191）

1 引言

基于短脉冲的超宽带信号具有大于几百兆赫兹的带宽，因此在密集散射信道环境中可以分辨大量的多径。这时，对于不同用户之间的通信链路，即使用户间距离很近，它们所经历的多径信道之间的相关性也很低[1,2]。利用超宽带信号的这一特性，可以进行基于空时聚焦的信号传输，即在发射端通过预滤波处理，使接收信号在给定的时间和位置形成聚焦峰值，而在其他的时间和位置只有微弱的旁瓣[3～5]。这种传输模式可以扩展单跳链路的传输距离[6,7]，还可以降低多用户传输时的用户间干扰[8,9]。

在超宽带通信中，采用信道的时间反演进行预滤波是实现空时聚焦的一种最简单的方式[10～12]。这时，物理信道表现为一个空时匹配滤波器。从时域来看，接收信号是一个低占空比信号，能量主要集中在聚焦峰值中，因此不仅降低了码间干扰，并且可以用低复杂度的单抽头接收机完成解调。从空域来看，强信号只出现在期望位置，因此可以降低同信道共存用户之间的互相干扰。但是，这种方案的性能依赖于信道响应的自相关和互相关特性，因此当信道特性不好时，用户之间的干扰较大。为了在各种信道环境下都具有良好的干扰抑制能力，可以基于迫零（ZF）准则或者最小均方误差（MMSE）准则来设计预滤波器[13～15]。

由于超宽带信号的发射功率谱密度受限，其单跳传输距离也非常有限。为了扩展超宽带通信系统的覆盖范围，利用中继进行多跳转发是一种有效的方式[16～19]。其中，文献[16]考虑了一对源节点和目的节点之间并行中继传输的问题，研究了2种分布式协作中继方法。文献[17]研究了传统三节点协作分集方案在跳时超宽带系统中的误码性能。文献[18]研究了两跳中继与多输入多输出技术相结合对超宽带系统的性能改善。与窄带信号不同，超宽带信号是一种扩频信号，可以在同一频带内通过跳时等方式实现多用户传输。因此，一个中继可以实现从多个源节点到多个目的节点之间的转发。如果每个发射节点都采用空时聚焦预处理，则中继节点以及目的节点的接收复杂度会大大降低。文献[19]考虑了应用空时聚焦技术进行多源单中继传输的问题，但其性能分析比较简单，没有考虑节点位置随机分布的影响，也没有考虑在广播阶段对多用户信号进行时分传输。

本文研究基于空时聚焦传输的多源单中继超宽带通信系统的性能，通过分析多址阶段和广播阶段的中断概率，得到各种条件下系统的可达吞吐量。在多址阶段，每个源节点使用预均衡以随机的时延发射信号，这相当于以随机时分的方式来访问信道。时隙数目越多，用户间可能的冲突越小，但是脉冲重复频率降低会导致单用户数据率的下降。在广播阶段，中继节点采用各自信道的时间反演对发往各目的节点的信号进行预滤波，并给这些信号等间隔的发射时延，这相当于以码分与时分相结合的方式来访问信道。信道响应越长，等效的扩频增益越大，但是用户间互相干扰的可能性也越大。因此，需要系统化地分析各种参数对网络性能的影响，传输方案设计也要考虑各方面因素之间的最优平衡。

本文安排如下：第2节给出中继网络的结构、超宽带信道模型以及基于空时聚焦传输时发射信号和接收信号的表达式；第3节分析多址阶段和广播阶段的中断概率以及网络的可达数据率；第4节通过仿真验证理论分析的结果；最后是结束语。

2 系统和信号模型

考虑如图1所示的超宽带中继网络，其中包括K个源节点、K个目的节点和一个中继节点，每个源节点有一个对应的目的节点，所有源节点到目的节点之间的通信都通过唯一的中继节点进行转发。假设中继节点位于坐标原点，源节点和目的节点在半径为D的圆内随机均匀分布。中继节点采用时分半双工模式。在第一个时隙里多个源节点向中继节点发送信号，此阶段为多址阶段；在第二个时隙里中继节点向多个目的节点发送信号，此阶段为广播阶段。

图1 多源单中继多目的节点的协作网络

考虑脉冲幅度调制的超宽带信号

其中，s(k)(t)表示第k个用户的发射信号， Pt是平均发射功率，是第k个用户发送的第i个符号，p( t)是宽度为 Tp、能量归一化的超宽带窄脉冲，Ts是脉冲重复周期（在超宽带通信里也叫做帧周期）。在每个帧周期里，存在Ns=Ts/Tp个时隙。

源节点k到中继节点r之间多径信道的冲激响应为

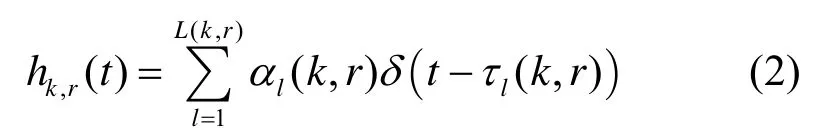
其中，L( k, r)是多径的条数，αl(k, r)和τl(k, r)分别是第l条径的幅度和时延，在脉冲超宽带系统里，幅度αl(k, r)是实数。中继节点r到目的节点k′之间的信道响应hr,k′(t)具有类似的表达形式。

信道的功率延迟剖面一般服从指数衰减，即

其中，τRMS是信道的均方根（RMS）时延扩展，这里有

空时聚焦传输方案需要发射端已知信道信息，处理的复杂度也集中在发射端。在多址阶段中，每个源节点可以用信道的逆响应进行预滤波，即进行预均衡，以压缩多径信道时延对信号的扩展。在广播阶段中，如果要同时消除多径干扰以及用户间干扰，即进行最优空时聚焦传输，则可以基于ZF或MMSE准则设计预滤波器。但是，实现这2种预滤波器需要较高的计算复杂度。为了降低中继的计算负担，在广播阶段可以采用时间反演进行预滤波。

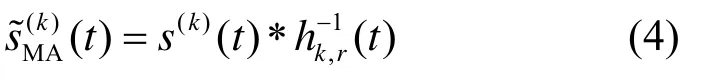
其中，符号“*”表示卷积操作。

在中继节点r处，接收信号是K个源节点的发射信号经过各自多径信道以后叠加的结果，即

其中，Ak,r是源节点到中继节点之间信道的大尺度衰落，τk,r是传播时延，z(t)是中继节点处的接收机热噪声。因为预滤波器与多径信道的卷积是一个冲激函数，所以在时刻t=iTs+τk,r会有一个聚焦峰值，这是源节点k的期望信号。K个源节点的信号在中继处最多会形成K个聚焦峰值。

中继节点的接收机可以直接在聚焦峰值处采样，而后进行检测或判决。第k个源节点的采样信号可以表示为

在广播阶段，中继节点共发出K路信号，每一路信号进行不同的幅度加权，即在发射端进行功率控制，以保证信号到达目的节点时具有足够高的信噪比。为了尽量降低用户之间的干扰，发送给目的节点k′的信号用hr,k′(-t )进行预滤波并进行kTs/K的时间延迟，即发射信号为

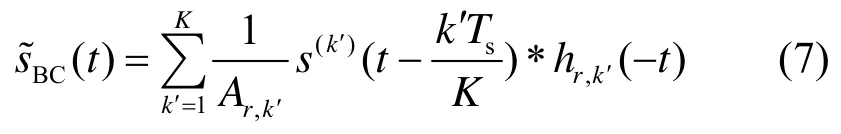
因为有K个用户，把帧周期分成了K份，即相邻2个用户之间的时间间隔为Ts/K。

经过各自的多径信道以后，目的节点k′的接收信号为

式中第二个等号后的第一项表示目的节点k′的期望信号，它在t=iTs+k ′Ts/K+τr,k′时刻存在聚焦峰值；第二项表示多用户干扰信号，因为hr,j′(-t )和hr,k′(t )不匹配，干扰信号没有聚焦峰值，表现为低功率的随机过程；z(k′)(t)是目的节点的接收机热噪声。

目的节点的接收机只需要在聚焦峰值时刻进行采样，而后进行判决，就可以完成检测。

3 网络可达数据率分析

不管是在多址阶段还是在广播阶段，多源单中继网络的传输性能主要受多用户干扰的影响。因此，下面首先分析多址阶段和广播阶段中由于多用户干扰所导致的中断概率，然后再优化帧周期、信干噪比等链路参数从而使网络的吞吐量最大。

3.1 多址阶段中断概率

在多址阶段，来自不同源节点的信号以随机的时延到达中继节点，由于传播距离的不同，信号到达中继节点时的接收功率也不相同。对于来自某一源节点的聚焦峰值，在同一时刻到达的其他源节点信号所形成的聚焦峰值都可能对它产生干扰。如果这些干扰的和功率超出了它所期望的信干噪比门限，则这一源节点到中继的传输就会发生中断。把这种由多用户干扰导致的传输错误概率叫做中断概率。

下面首先推导同一时刻到达的若干路干扰信号的和功率的概率分布，然后再分析这些聚焦峰值在时间上发生冲突的概率，最后给出多址阶段每条链路的传输中断概率。

源节点的位置在以中继为圆心，半径为D的圆内均匀分布，所以源节点到中继节点距离d的概率分布为

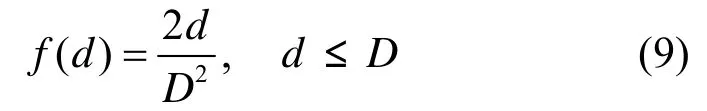
接收信号功率依赖于传播距离d和路径损耗因子α，也就是

因为中断概率主要受各用户接收功率相对大小的影响，为了便于推导，用0P Dα-对rP进行归一化，得到归一化接收信号功率：

利用式(9)可以导出λ的概率密度函数为

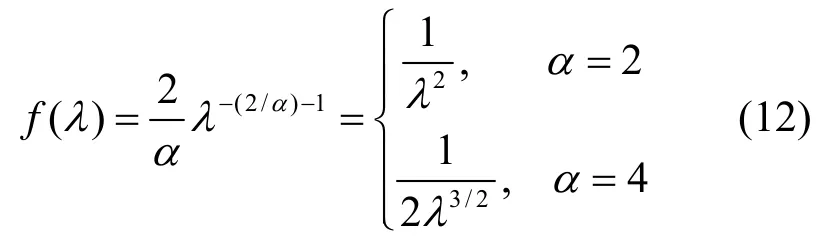
其中，1λ≥。可以看出λ是一种长拖尾分布，即它的尾部概率以幂函数的形式衰减而不是以指数函数的形式衰减[20]。

如果有多个用户的峰值信号同时到达，这些峰值信号和功率的概率密度函数应该是式(12)的多重卷积，不存在解析解。文献[9]中曾用2种稳定分布，即柯西（Cauchy）分布和勒维（Levy）分布[20]，来分别近似式(12)中当2α=和4α=时的2个概率密度函数。稳定分布具有良好的叠加特性，即具有稳定分布的多个独立随机变量之和仍然服从稳定分布。因此，用稳定分布来近似表达归一化接收信号功率的概率分布，可以导出中断概率的解析解。

根据文献[9]中的结果，当n个用户的峰值信号同时到达时，其和功率nΛ的累积分布函数（CDF）为

其中，erfc(·)是互补误差函数。

不失一般地，下面以源节点k为例，来研究它到中继节点传输中断的概率。此时源节点k为期望用户，其他用户都是干扰用户。

源节点k到中继的距离为dk，代入式(11)，可以得到其归一化接收功率λk=(dk/D)-α。假设这条链路可靠通信所需要的信干噪比为β= λk/(λN+λI)，其中λN是归一化噪声功率，λI是归一化干扰功率。给定信干噪比也就决定了用户可以采用的调制方式，它与帧周期一起决定了此链路所能达到的数据率，将在3.3节对这2个参数进行优化。

如果用户k的接收信噪比为γ，即λk/λN=γ，那么可以计算出干扰功率的容限为

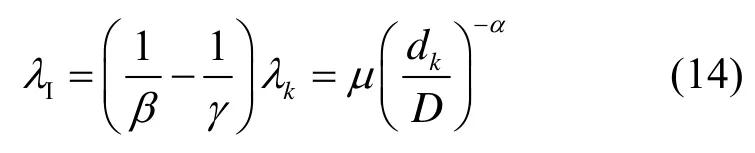
其中，μ=1/β-1/γ，当干扰功率远大于噪声功率时，μ≈1/β。在接收端对期望用户信号进行采样的时刻，如果干扰信号的和功率超过λI，则通信会发生中断。

首先假设有n个用户的峰值同时到达并干扰了第k个用户的信号，这时用户k的数据传输发生中断的概率为

其中，erf(x)=1-erfc(x)是误差函数。

考虑脉冲波形的影响，每个用户聚焦峰值的持续时间为Tp。考虑到帧长是Ts，某一干扰用户的聚焦峰值与期望用户的聚焦峰值在时间上发生冲突的概率为

因为一共有K个用户，出现n个用户同时干扰期望用户的概率为

期望用户的平均中断概率为所有可能的时间冲突概率与干扰超过期望用户容限概率的乘积再求和，即

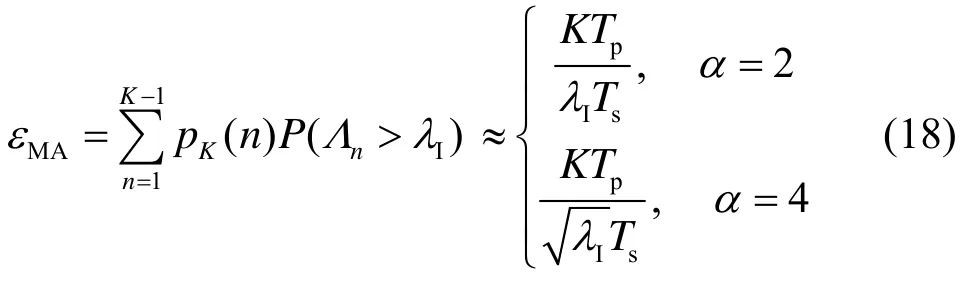
在上式的推导过程中利用了等式关系

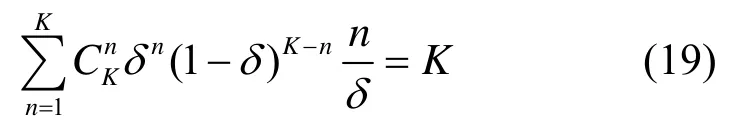
以及线性化近似

3.2 广播阶段中断概率

在广播阶段，只有期望用户的信号会在目的节点处形成聚焦峰值，其他用户的信号在接收端只形成散乱的干扰。

以目的节点k′为例，由式(8)可知，其期望信号经过的预滤波和实际物理信道合成的等效信道为，接收信号在0t=时刻有一个聚焦峰值，峰值的能量为。因为峰值信号的持续周期为2Tp，因此它的平均功率为1/2Tp。

中继发给目的节点j′的信号到达目的节点k′时成为干扰信号。从中继到目的节点k′所经过的等效信道为，这是一个随机过程，其平均功率为

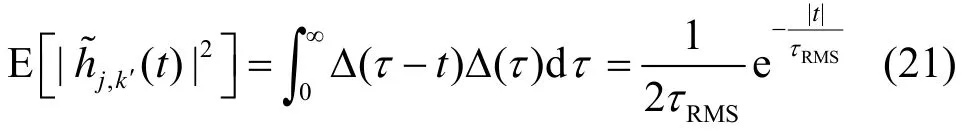
其中，第一个等式来源于2个信道的不相关特性。

由式(21)可以看出，干扰信道的平均功率在不同的时延处呈现双边指数衰减。为了得到随机扩频增益和冲突概率的显式表达，把它近似为一个具有同样面积的矩形函数。近似的程度会在后面的仿真中进行分析。

因为干扰信道的和功率为

且式(21)的最大值为1/2τRMS，所以当矩形的高度与双边指数函数的最大值相同的时候，其宽度为2τRMS。也就是说经过近似以后，干扰信道功率的大小为1/2τRMS，持续时间为2τRMS。

由于期望信道响应的功率为1/2Tp，干扰信道响应的功率为1/2τRMS，可见经过预滤波和多径信道的共同作用产生了如下的扩频增益：

它反映了时间反演预滤波通过随机码分多址方法抑制干扰的能力。

因为帧长是Ts，用户间的时延为Ts/K，每一个用户可能干扰的时间范围为2τRMS，所以对期望用户的峰值而言，同时存在的干扰用户数目为

假设目的节点k′与中继节点之间的距离为d′k，其干扰容限为λ′I。由于扩频增益的存在，只有干扰信号的和功率超过GSλ′I时才会引发链路的中断，因此利用式(15)可以导出广播阶段的中断概率为

3.3 网络可达数据率

由上面推导得到的多址阶段和广播阶段的中断概率，可以计算一个源节点经过中继到达一个目的节点的传输数据率。根据前面的定义，在给定信干噪比和帧周期的情况下，源节点发射时的最大数据率为

经过多址阶段和广播阶段的多用户干扰以后，源节点k到目的节点k′的吞吐量为

把式(18)和式(25)代入上式，并应用近似关系λI≈ λk/β，可得

在式(28)中，帧周期Ts与可靠通信所需要的信干噪比β是2个可以优化的参数，通过交替优化的方法可以得到它们的联合最优解。

首先，固定β，这时可以看出Rt是Ts的三次函数，存在一个极小值和一个极大值。使Rt对Ts的导数等于零，可以得到使网络吞吐量最大的帧周期：

其中

然后，把Ts的最优取值代入式(28)，可以看到当2α=时与β有关的项为lb(1+β)/β，当4α=时与β有关的项为lb(1+β)/β，由此不难导出β的最优值为

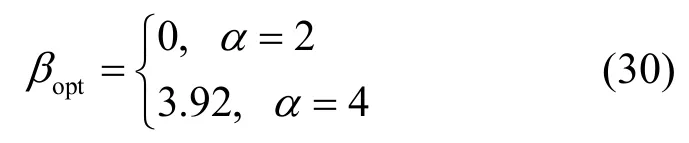
把式(29)和式(30)的结果代入式(28)，可以得到从源节点k到目的节点k′的最大吞吐量为

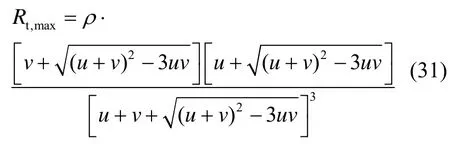
其中，u和v的定义与式(29)中相同，而

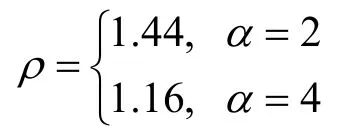
当dk=d′k时，可以得到最优帧周期Ts,opt和最大吞吐量Rt,max的更简单的表达式：

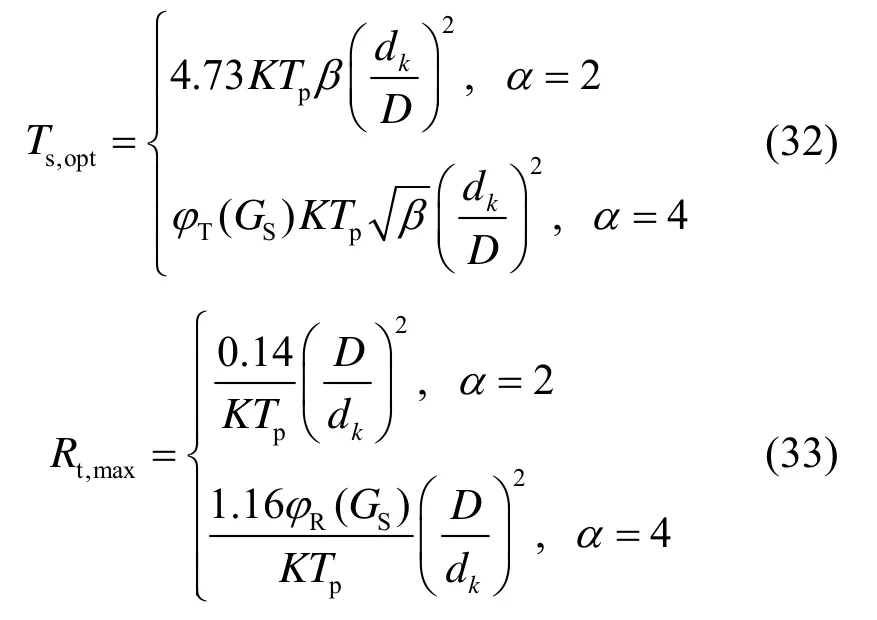
其中，φT(GS)与φR(GS)是2个与扩频增益GS有关的函数，由式(23)可知，当信道时延扩展和脉冲宽度不变时，它们是2个定值。

下面，一一分析上述优化设计的结果，从而给出设计实际系统传输方案以及相关参数的准则。

根据式(30)的结果可见，当路径损耗因子2α=时，可靠通信所需要的信干噪比选得越低越好，即这时最好采用低码率的纠错编码、二进制的调制方式、以及较长的扩频序列。而当路径损耗因子4α=时，最优的接收信干噪比为6 dB（即β=3.92），这是一般非扩频通信系统的典型工作点[21]。

从式(32)可以看出帧周期的最优取值与其他参数的关系。当2α=时，Ts,opt与信干噪比β成正比，因为β趋于零时网络的吞吐量最大，所以帧周期的取值也应该尽量的小；当α=4时，Ts,opt与成正比，因为这时β最优值为3.92，把其他参数代入式(32)可以得到帧周期的最优取值。不管α=2还是α=4，Ts,opt与用户数目K、脉冲宽度Tp、以及(dk/D)2都是正比的关系，因为Ts/ Tp=Ns是帧周期里的时隙个数，随着用户数的增多，Ns也应该线性增长，这样才能降低用户之间的碰撞概率和相互干扰。在其他参数不变的情况下，帧周期应该随距离的平方增长，因为距离越远的用户接收功率越小，越容易受到其他用户的干扰，增加帧周期可以降低这些用户被干扰的概率。

网络的最大吞吐量是在帧周期和接收信干噪比都取最优值时得到的。从式(33)可以看出，Rt,max与K、Tp、以及(dk/D)2成反比。这说明一个中继同时服务的用户数目直接影响通过它进行转发的一对节点间可能达到的数据率。而节点与中继的距离也会以平方律的关系影响可达数据率。

当部署一个实际的超宽带中继网络时，已知节点的数目、各节点的活动范围、所采用的超宽带脉冲宽度以及信道时延扩展，就可以计算出各对节点间所能达到的最高数据率。如果计算结果不能满足实际网络的性能需求，就应该考虑重新划分网络拓扑，通过采用更多的中继节点等措施，来提高网络的吞吐量。

4 仿真验证

本文通过采用较为实际的信道模型进行仿真，来验证3.1节和3.2节中推导的多址阶段和广播阶段中断概率的正确性。

设源节点和目的节点均匀分布在以中继为中心、半径D=1 000m的圆内。期望用户，即多址阶段的源节点k和广播阶段的目的节点k′，距中继的距离dk=dk′=100m。考虑期望用户的接收信噪比为10dB，可靠通信所需要的信干噪比为4dB，因此归一化干扰功率容限为λI=0.3λk，λI′=0.3λk′。发射脉冲宽度Tp=1 ns，帧周期Ts=100 ns。采用IEEE 802.15.4a信道模型中的“CM2”环境（居民区非直射路径）来产生多径信道响应[22]，所产生信道的多径时延扩展为τRMS=10ns。

图2和图3分别给出了通过理论计算和仿真得到的多址阶段和广播阶段的中断概率随节点个数的变化情况。考虑节点数目从3增加到100，对路径损耗因子为2和4这2种情况分别得到了数值和仿真结果。

从图中可以看出，对于多址阶段期望用户的中断概率而言，理论推导与仿真的结果几乎完全重合；而对广播阶段的中断概率而言，理论推导与仿真结果略有偏差，但基本趋势完全一致。这些结果验证了本文对中断概率推导的正确性，也表明在推导过程中所引入的几处近似对分析结果影响不大。

图2 多址阶段用户的中断概率

图3 广播阶段用户的中断概率

另外，对于多址阶段，从式(18)可以看出，由于预均衡的作用，多径时延扩展的大小不影响多址阶段的中断概率，并且α=2时的中断概率总大于α=4时的中断概率。对于广播阶段，从式(25)可以看出，当α=2时，中断概率也不受多径时延扩展的影响，这时随机扩频增益与时间冲突概率的影响互相抵消；当α=4时，多径时延越大中断概率也越大，并且可能大于α=2时的值。

5 结束语

本文研究了基于空时聚焦传输的超宽带中继系统的性能。当多个源节点和多个目的节点共用一个中继节点进行通信时，源节点的发射端采用单用户预均衡方案、中继节点的发射端采用多用户时间反演方案，可以降低中继节点的计算负担并保证良好的通信性能。在这种多源单中继模式下，多用户干扰是影响网络吞吐量的关键因素。本文首先推导了多址阶段和广播阶段用户的中断概率，然后导出了从源节点到目的节点可达数据率的解析表达式。对可达数据率进行分析，揭示了用户数、脉冲宽度、源节点和目的节点到中继节点的距离、节点分布的范围等与可达数据率之间的内在联系，从而提供了在不同信道环境下设计发射信号帧周期、编码调制方式以及扩频码长度的准则。

[1] KEIGNART J. UWB SIMO channel measurements and simulations[J].IEEE Transactions on Microwave Theory and Techniques, 2006, 54(6):1812-1819.

[2] ZHOU C, GUO N, QIU R C. Time-reversed ultra-wideband (UWB)multiple input multiple output (MIMO) based on measured spatial channels[J]. IEEE Transactions on Vehicular Technology, 2009, 58(7):2884-2898.

[3] EMAMI M. Matched filtering with rate back-off for low complexity communications in very large delay spread channels[A]. ACSSC[C].Pacific Grove, California, USA, 2004. 218-222.

[4] STROHMER T. Application of time-reversal with MMSE equalizer to UWB communications[A]. GLOBECOM[C]. Dallas, Texas, USA,2004. 3123-3127.

[5] GUO N, SADLER B M, QIU R C. Reduced-complexity UWB time-reversal techniques and experimental results[J]. IEEE Transactions on Wireless Communications, 2007, 6(12): 4221-4226.

[6] HUSSAIN M G M. Principles of space-time array processing for ultrawide-band impulse radar and radio communications[J]. IEEE Transactions on Vehicular Technology, 2002, 51(5): 393-403.

[7] DOWLA F, SPIRIDON A. Spotforming with an array of ultra-wideband radio transmitters[A]. UWBST[C]. Reston, Virginia,USA, 2003. 172-175.

[8] NGUYEN H T, KOVCS I Z, EGGERS P C F. A time reversal transmission approach for multiuser UWB communications[J]. IEEE Transactions on Antennas and Propagation, 2006, 54(11): 3216-3224.

[9] TIAN Y, YANG C. Spatial user capacity of UWB networks with space-time focusing transmission[A]. ICC[C]. Cape Town, South Africa, 2010. 1-6.

[10] NGUYEN H T. Time reversal in wireless communications: a measurement-based investigation[J]. IEEE Transactions on Wireless Communications, 2006, 5(8): 2242-2252.

[11] LIU X. Post-time-reversed MIMO ultrawideband transmission scheme[J]. IEEE Transactions on Antennas and Propagation, 2010,58(5): 1731-1738.

[12] EL-SALLABI H. Experimental investigation on time reversal precoding for space-time focusing in wireless communications[J]. IEEE Transactions on Instrumentation and Measurement, 2010, 59(6):1537-1543.

[13] LIU Z, TIAN Y, YANG C. A preprocessing algorithm of ultra- wideband signal for space-time focusing transmission[A]. ICSP[C]. Beijing,China, 2008. 1896-1899.

[14] NGUYEN H. On the MSI mitigation for MIMO UWB time reversal systems[A]. ICUWB[C]. Vancouver, Canada, 2009. 295-299.

[15] CHANG Y H. Codeword design for ultra-wideband (UWB) precoding[J]. IEEE Transactions on Wireless Communications, 2010, 9(1):198-207.

[16] ZHU S, LEUNG K K, CONSTANTINIDES A G. Distributed cooperative data relaying for diversity in impulse-based UWB ad-hoc networks [J]. IEEE Transactions on Wireless Communications, 2009,8(8): 4037-4047.

[17] ZEINALPOUR Z, NASIRI M, AAZHANG B. Bit error probability analysis of UWB communications with a relay node [J]. IEEE Transactions on Wireless Communications, 2010, 9(2): 802-813.

[18] MAICHALERNNUKUL K, ZHENG F, KAISER T. Design and performance of dual-hop MIMO UWB transmissions[J]. IEEE Transactions on Vehicular Technology, 2010, 59(6): 2906-2920.

[19] TIAN Y, YANG C. Space-time focusing transmission in ultra-wideband cooperative relay networks[A]. ICUWB[C]. Vancouver,Canada, 2009. 353-358.

[20] NOLAN J P. Stable Distributions[M]. Boston: Birkhauser, 2002.

[21] PROAKIS J G. Digital Communications (4th ed.)[M]. New York:McGraw-Hill, 2001.

[22] MOLISCH A F. Ultrawideband propagation channels - theory, measurement, and modeling[J]. IEEE Transactions on Vehicular Technology, 2005, 54(9): 1528-1545.