H布尔函数的相关免疫性与重量的关系

黄景廉，王卓

（西北民族大学 计算机科学与信息工程学院，甘肃 兰州 730030）

1 引言

在现代密码学中，杨义先教授提出的H布尔函数及对 H布尔函数的研究[1～4]，为布尔函数密码学性质的研究开辟了一个重要的、新的研究方向和研究领域。由于密码系统抵抗各种攻击的综合能力的要求，要求设计的布尔函数要兼具扩散性、相关免疫性、代数免疫性等密码学性质。可知，直接讨论H布尔函数的相关免疫性要比单纯地、孤立地讨论布尔函数的相关免疫性更有意义，能更直接地对扩散性、相关免疫性等直接进行综合性研究。H布尔函数为各种密码学性质的综合研究提供了一个方向性工具，有重要的密码学价值。本文正是在这一方向上来讨论扩散性、重量和相关免疫性的关系问题。在H布尔函数存在的重量范围内，H布尔函数的相关免疫性及其阶数与它的重量有何直接关系的问题，是一个可以直接从H布尔函数的重量即可便捷地、明确判定H布尔函数的相关免疫性及其阶数的重要问题，也是人们尚未顾及研究的问题。由于布尔函数 f(x)的导数只能反映 f(x)在 df(x)/dxi=1（这时相应有 ef(x)/exi=0）的取值情况，只有定义布尔函数 f(x)的 e-导数[5～7]，才能反映 f(x)在 ef(x)/exi=1（而这时相应有df(x)/dxi=0）时的另一种取值情况。本文将导数和与导数一起才能完整刻画布尔函数的重量而定义的e-导数相结合作为研究工具，讨论了在 2n-2≤w(f(x))≤2n-1+2n-2这一大的重量范围内，各种重量H布尔函数的相关免疫性及其阶数的存在性问题，以及m (m≥2) 阶相关免疫函数的阶数m与函数的维数n有何关系的问题，得到一系列有用的明确结果。

2 预备性概念

布尔函数的导数是布尔代数、逻辑设计和密码学中早已有定义的概念[8,9]，但e-导数是为刻画布尔函数的重量才定义的新概念。为后面讨论各种不同重量 H布尔函数的相关免疫性及其阶数的需要和阅读方便，下面给出导数和e-导数的定义以及它们与布尔函数、重量、扩散性、相关免疫性的一些最基本的简单关系。

定义1 n元布尔函数f (x)对变元xi1,…, xir的e-导数，记为ef (x)/e(xi1,…, xir)，并定义为

其中，f(x)对单个变元xi(i=1, 2,…, n)的e-导数，记为ef(x)/exi, (i=1, 2,…, n)。经简单推导，有如下便于使用的形式：

由定义1和布尔函数的导数的定义，可直接得到下面的引理1和引理2。

引理1 有乘积关系df (x)/dxie f (x)/exi=0，(i=1,2,…, n)。

引理2 对任意n元布尔函数f(x)，有如下关系。

1) f (x)=f(x)∂f(x)/∂(xi1,…, xir)+ef(x)/ e(xi1,…, xir)，(1≤r≤n, 1≤ i1＜i2＜…＜ir≤n)。

2) f (x)= f(x)d f(x)/dxi+e f(x)/exi，(i=1, 2,…, n)。

3) w(f(x))=w(f(x)∂ f(x)/ ∂(xi1,…, xir))+w(ef(x)/e(xi1,… , xir))=2-1w(∂f (x)/ ∂ (xi1,… , xir))+w(e f(x)/e(xi1,…, xir))，(1≤r≤n, 1≤ i1＜i2＜…＜ir≤n)。

4) w(f (x))=w(f (x)df(x)/dxi)+w(ef (x)/ exi)=2-1w(df (x)/dxi)+w(ef (x)/exi)，(i=1, 2,…, n)。

[4]关于扩散性的定义显然可由导数来描述，于是可得出关于f (x)的扩散性的等价定义引理3。

引理3 布尔函数f (x)满足k (1≤k≤n)次扩散准则，当且仅当对一切 xi1,…, xik，(1≤k≤n, 1≤i1＜i2…＜ik≤n)，有

w(∂f(x)/∂(xi1,…,xik)=2n-1，(1≤k≤n, 1≤ i1＜i2＜…＜ik≤n)

特别地，f (x)满足一次扩散准则，当且仅当对一切 xi，(i=1, 2,…, n)，有

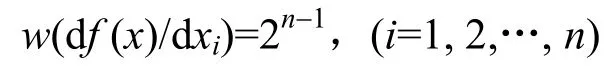
由引理2的4)和引理3，可以用导数和e-导数来导出和参考文献[4]p19、p133、p22关于平衡 H布尔函数的定义等价的定义，即引理4。

引理4 f(x)是平衡H布尔函数，当且仅当对一切 xi(i=1, 2,…, n)，有

w(df(x)/dxi)=2n-1，且 w(ef(x)/exi)=2n-2，(i=1, 2,…, n)

下面的引理5是一些文献中已有的结果，这里引入是因为本文的讨论要用。本文也将给出用导数性质进行的证明。

引理5 布尔函数f(x)是H布尔函数的必要条件是 2n-2≤w(f (x))≤2n-1+2n-2。

证明 若f (x)是H布尔函数，则由引理3知，必有w(df (x)/dxn)=2n-1，又由引理2的4)知，必有w(f(x))≥2-1w(df (x)/dxn)=2n-2。

对w(f(x))≤2n-1+2n-2用反证法证明。

假设 w(f(x))＞2n-1+2n-2，则有 w(1+f(x)) =2n-w(f(x))＜2n-2，故由引理 2，必有 w(d (1+f (x))/dxn) ＜2n-1。但由导数的性质知，有 w(df(x)/dxn)=w(d (1+f(x))/dxn)＜2n-1，故由引理3知，这与f(x)是H布尔函数矛盾，故必有w(f(x))≤2n-1+2n-2。

故若 f(x)是 H 布尔函数，必有 2n-2≤w(f(x))≤2n-1+2n-2。

3 对 H布尔函数的重量与相关免疫性及其阶数关系的讨论

下面对2n-2≤w(f (x))≤2n-1+2n-2中所有H布尔函数的相关免疫性及其阶数进行讨论，同时给出一些有关的辅助性定理。

定理 1 对布尔函数 f (x)（x∈GF(2)n，f (x)≠c，c∈GF(2)），若

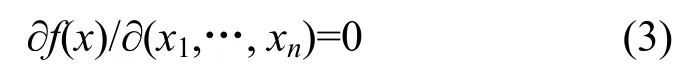
则f(x)必为一阶相关免疫函数。

证明 若 f(x)满足式(3)，则对一切 i=1, 2,…, n，显然必有

故知f(x)为一阶相关免疫函数。

定理1及式(4)是参考文献[4]p47中相关免疫的一个充要条件。式(3)是式(4)的一个充分条件，故式(3)只是f(x)一阶相关免疫的充分条件，而不是必要条件。

例如：f(x)=x4+x1x4+x2x4+x2x5+x3x4+x4x5+x1x2x4+x1x2x5+x1x3x4+x1x3x5+x1x4x5+x2x3x4+x2x3x5+x3x4x5

f(x)是一阶相关免疫函数，但不满足式(3)。

定理2 若n元布尔函数f1(x)和f2(x)有w(f1(x))=w(f2(x))，且

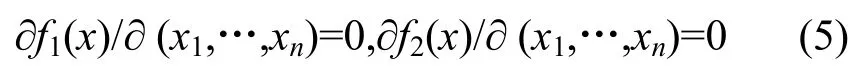
则f1(x)和f2(x)的级联函数

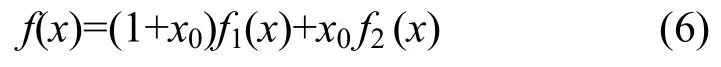
是n+1元一阶相关免疫函数。

这里要注意的是，式(6)与一些参考文献[4]P163、参考文献[1]P16、P48中定义的级联函数

不仅形式不同，而且有本质的差异，这一点是显然的。

证明 由于w(f1(x))=w(f2(x))，则由式(6)知有

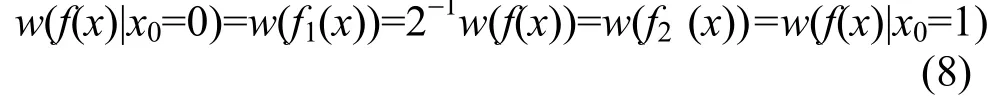
由于式(5)，则由定理1知f1(x)和f2(x)均为n元一阶相关免疫函数。故对i=1, 2,…, n，ai∈GF(2)，必有

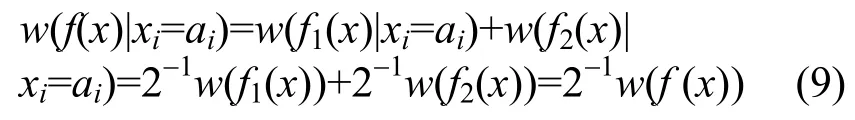
结合式(8)、式(9)，便知f(x)是n+1元一阶相关免疫函数。证毕。

定理1和定理2说明了一阶相关免疫函数f(x)取值的某种对称性。而由一阶相关免疫定义的充要条件式(4)来看，这种对称性是充分必要的性质。显然，定理2还可作进一步的多次级联的推理。限于篇幅，这里省略。

有了上面的准备，下面来讨论各种重量H布尔函数的相关免疫性。

下面对w(f(x)) =2n-1+2n-2的m 阶(m≥1)相关免疫性分成几个定理来证明。

定理3 在w(f(x))=2n-1+2n-2的H布尔函数中，存在二阶相关免疫的H布尔函数。

证明 为推导公式明晰的需要，这里要从一阶相关免疫推起（因为由定理1和定理2知，一阶肯定存在）。设f(x)是w(f(x))=2n-1+2n-2的H布尔函数，经简单推导，有

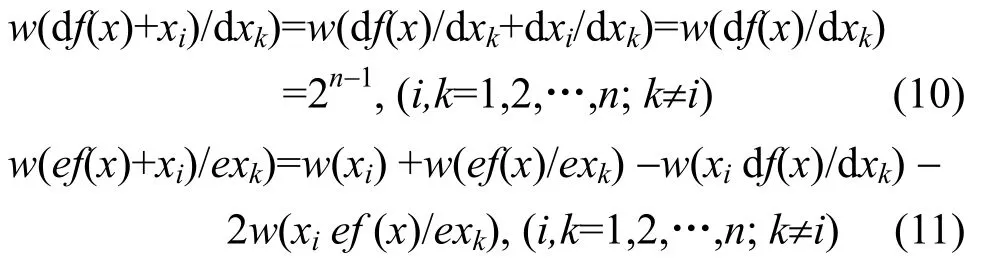
于是由式(10)、式(11)、引理4和相关免疫的条件（w(f (x) +xi)=2n-1）要求知，f(x)一阶相关免疫，当且仅当

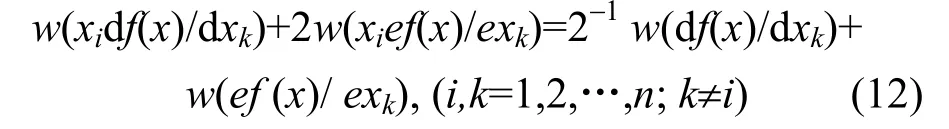
由于f(x)是H布尔函数，且w(f(x))= 2n-1+2n-2，则由引理2、引理3知，必有

w(df(x)/dxk)=2n-1，w(ef(x)/exk)=2n-1，(k=1, 2,…,n)，故由引理1知，必有

反之，显然满足式(13)的 H布尔函数，必有w(f(x))=2n-1+2n-2，w(ef(x)/exk)=2n-1。

又由于 w(xi) =2n-1, (i,=1,2,…,n)，故由式(13)知，必有

将式(14)展开，并由引理1知有

解式(12)、式(15)两式组成的联立方程组，则对一切 i,k=1,2,…,n，k≠i，有解

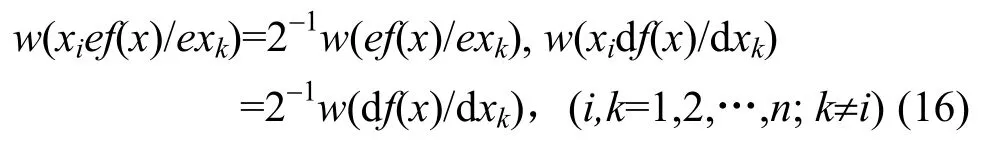
于是可知，当f(x)一阶相关免疫时，必有式(12)成立，而式(15)是必成立的。故必有式(16)两式均成立。反之，若式(16)成立时，显然将式(16)代入式(12)，式(12)必成立。故f(x)一阶相关免疫，当且仅当式(16)成立。

由于式(15)必成立及式(16)是方程组唯一解，可知，式(16)中有一式成立，则另一式也必成立。于是取 fe(x)=ef(x)/exn，即 f1(x)是由 f(x)中 ef(x)/exn=1 且df(x)/dxn=0的那些值的函数，即有 w(fe(x))=w(ef(x)/exn)=2n-1。而满足式(16)第一式的 fe(x)显然是存在的。比如满足定理 1的条件∂fe(x)/∂ (x1,…,xn)=0，或满足定理 2 的条件∂fe(x)/∂ (x1,…, xn)=0，或满足对定理 2进行推广的条件∂fe(x)/∂(xn-2xn-1xn)=0 的 fe(x)（由于 w(fe(x)) = 2n-1，fe(x)) = ef(x)/exn）是存在的。这时，fe(x)显然都满足式(16)的第一式。故知相应的f(x)也满足式(16)的第一式，故f(x)也满足式(16)的第二式。事实上，取∂fe(x)/∂ (xn-2xn-1xn)=0的条件，便知f(x)可由f1(x)=xn-1+xn+xn-1xn；f2(x)=1 +xn-1+xn-1xn；f3(x) =1+xn-1xn；f4(x)=1+xn+xn-1xn这4个2元布尔函数按保证f (x)是H布尔函数，及满足∂fe(x)/∂(xn-2xn-1xn)=0的某种次序逐步级联构成。故知由式(16)第一式，易于构造出一阶相关免疫函数，即一阶相关免疫的w(f(x))= 2n-1+2n-2的H布尔函数是存在的。

于是取f(x)是w(f(x))=2n-1+2n-2的一阶相关免疫的 H布尔函数，并对它的二阶相关免疫性进行讨论。经简单推导，有

由引理 4和式(12)、式(13)、式(17)、式(18)及二阶相关免疫条件知，f(x)二阶相关免疫，当且仅当

由于式(13)必成立，又由于 w(xixj)=2n-2, (i,j=1,2,…,n; i≠j)，故必有

求解式(19)、式(20)两式组成的联立方程组，则对一切 i,j,k=1,2,…,n，k≠i≠j，有解

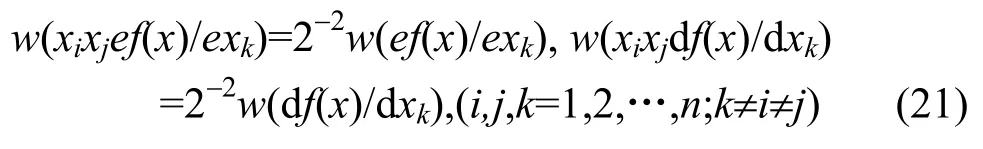
显然，通过和前面一阶相关免疫相同的讨论，可得结论：f(x) 二阶相关免疫，当且仅当式(21)成立。

利用前面一阶相关免疫时得出的 f1(x)、f2(x)、f3(x)、f4(x)，便能轻易构造w(f(x))=2n-1+ 2n-2的二阶相关免疫函数。为对任意n元能更清楚地证明存在性，先构造2个低元的二阶相关免疫函数，然后再逐步级联成任意n元的方法来构造。为此，先证明如下关系。

若fi1(x)和fi2(x)均为m(m≥1)阶相关免疫n元H布尔函数，且w(fi1(x)+ fi2(x))= 2n-1，则 fi1(x) 和fi2(x)的级联函数：

仍至少是m阶相关免疫的n+1元H布尔函数，这是由于，对ωx (1≤w (ω)≤m)，经推导，有 w(f(x)+ ωx)=w((1+x0) fi1(x)+ωx)+w(x0fi2(x)+ωx)- w(ωx)，故知 f(x)仍为m(m≥1)阶n+1元布尔函数。又

即f (x)为n+1元H布尔函数。

于是由一阶相关免疫时得到的 f1(x)、f2(x)、f3(x)、f4(x)，根据式(21)第一式的要求，按 f1(x)、f2(x)、f3(x)、f4(x)、f4(x)、f3(x)、f2(x)、f1(x)的次序构造得ft(x)=1+ x1+ x2+ x3+ x4+ x5+ x1x2+ x1x3+ x1x4+ x2x3+x2x4+ x2x5+ x3x5+ x4x5

又按 f3(x)、f4(x)、f1(x)、f2(x)、f2(x)、f1(x)、f4(x)、f3(x)的次序构造得 fr(x)=1+x2+x1x2+x1x3+x1x4+x2x3+x2x4+x2x5+x3x5+x4x5，其中，ft(x)和 fr(x)均为 n=5元二阶相关免疫 H布尔函数。于是，将 ft(x)和 fr(x)按次序 ft(x)、fr(x)、fr(x)、ft(x)、fr(x)、ft(x)、ft(x)、fr(x)、…两两逐步级联，便可得到任意 n元二阶相关免疫的w(f(x))=2n-1+2n-2的H布尔函数。

故定理3成立。证毕。

从定理3证明中的式(16)、式(21)的推导，可以看出，w(f(x))= 2n-1+2n-2的H布尔函数的三阶相关免疫的充要条件，也有

如果用归纳法来证明，显然可以得到任意m (m≥1)阶相关免疫的充要条件。限于篇幅，不作详细推导，直接给出如下定理4。

定理4 w(f(x))=2n-1+2n-2的H布尔函数f (x)任意 m (m≥1)阶相关免疫的充要条件是，对一切S1≠S2≠…≠Sm≠k，m≥1，有

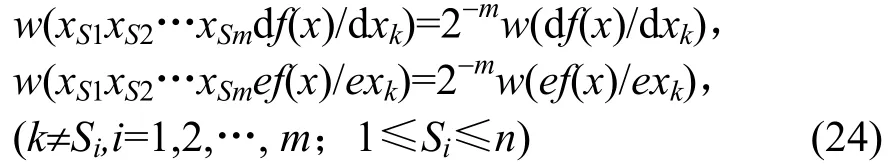
现在需要用 w(f(x))=2n-1且 ef (x)/exn=2n-1，df(x)/dxn=0的布尔函数中，存在任意m (m≥1)阶相关免疫布尔函数及定理 4，来证明存在w(f(x))=2n-1+2n-2的任意m (m≥1)阶相关免疫H布尔函数。下面先给出定理3、定理4的推论，然后再给出解决上述问题的定理5。

推论1 若ft(x)和fr(x)均为m (m≥1)阶相关免疫n元H布尔函数，且w(ft(x) +fr(x))=2n-1，则ft(x)和fr(x)的级联函数：

仍至少是m阶相关免疫的n+1元H布尔函数。

推论1在定理3中式(22)已证明，这里不再重复证明。

推论2 若f (x)为w(f(x))=2n-1+2n-2的H布尔函数，则f (x)为m (m≥1)阶相关免疫函数的充分必要条件是式(24)的第二式（或第一式）

成立。

证明 从定理3的推导便可知，f (x)为m (m≥1)阶相关免疫函数的充分必要条件是

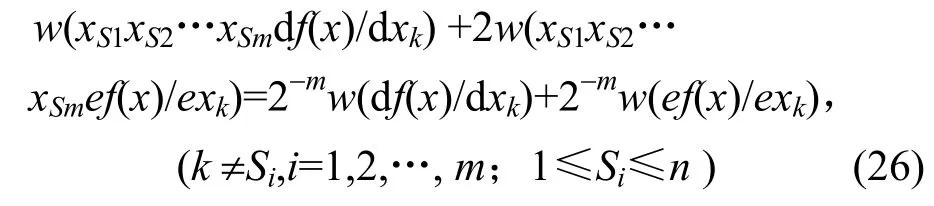
由于w(f(x))=2n-1+2n-2，w(df(x)/dxk)=2n-1，w(ef(x)/exk)=2n-1，(k =1,2,…, n )，则定理 3 有式(13)必成立，于是和定理3由式(13)推出式(14)、式(15)相仿。由于w(xS1xS2…xSm)=2n-m，(1≤Si≤n，i=1,2,…, m)，必有

将式(26)、式(27)两式联立成方程组并解之，得唯一解式(24)，故f (x)为m (m≥1)阶相关免疫函数的充分必要条件是式(24)的两式均成立。由于式(24)是方程组式(26)、式(27)的唯一解，故推论2成立。

显然，特别提出推论 2，是为以后判断w(f(x))=2n-1+2n-2的H布尔函数f(x)是否m (m≥1)阶相关免疫时，只需对ef (x)/exn=fS(x) 进行判断，这比同时判断式(24)的2个式子要省一半工作量。

定理 4和推论 2只是给出了判断 w(f(x))=2n-1+2n-2的H布尔函数是不是m (m≥1)阶相关免疫函数的充分必要条件，并没有给出它存在的结论。但推论2给出了判断它的存在性的简便方法。为此，下面给出定理5。

定理5 在w(f(x))=2n-1，且w(ef(x)/exn) =2n-1，df(x)/dxn= 0的 n (n ≥3)元布尔函数 f (x)中（即f(x)=ef(x)/exn），存在任意 m (m≥1) 阶相关免疫函数，且相关免疫阶数最高为m=n-2阶，即

max mi= m=n-2

证明 由定理条件w(f(x))= w(ef(x)/exn) =2n-1，f(x)= ef(x)/exn，则当n ≥3时，取f (x)满足

显然，即相应有

则由定理1、定理2及推论1知，f(x)必为一阶相关免疫函数。而且还可知，f(x)这时必定是由f21(x)=xn-1和 f22(x)=1+xn-1按式(25)让 x0依次取为xn-2,xn-3,…, x2,x1逐步级联得到的函数。而且由式(28)、式(29)知，f(x)必须在n≥3时，才至少是一阶相关免疫的。有以上结果后，下面便可用归纳法来推导f(x)的表示式及相应的相关免疫性质。

当 n=3，即 x=xn-2xn-1xn时，利用式(25)，取x0=xn-2，对 f21(xn-1xn)= xn-1和 f22(xn-1xn)=1+xn-1作级联，得

和

式(30)、式(31)中，f21(x)和 f22(x)是二元函数。显然，f31(x)和f32(x) 仍然是仿射函数[3,6]（线性函数）。

根据相关免疫的定义[3]：f(x)为m阶相关免疫，当且仅当对任意的1≤ i1≤i2≤…≤ir≤ n和满足1≤w(ω)≤ m 的ω=(ω1,…, ωn)∈GF(2)n，

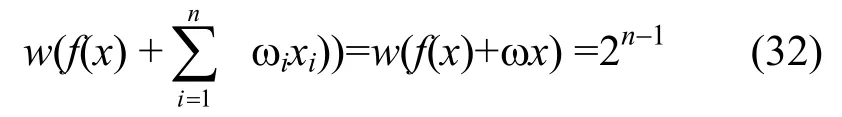
显然可知，三元函数（即n=3）f31(x)和f32(x) 均为一阶相关免疫线性函数，但一定不是二阶相关免疫函数。

同样，取n=4，即x=xn-3xn-2xn-1xn时，有

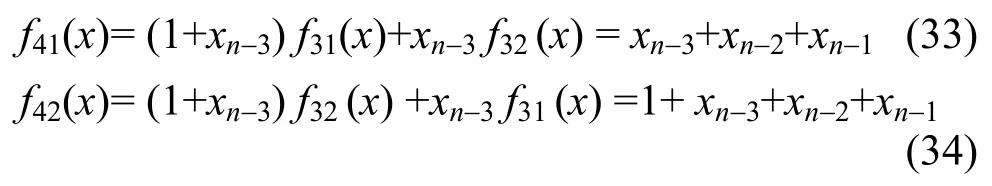
其中，f31(x)和 f32(x)是三元布尔函数。于是，显然由相关免疫的定义式(32)可知，f41(x)和f42(x) 均为二阶相关免疫线性函数，但一定不是三阶相关免疫函数。

现在用归纳法，假设n=k时，依x0=xn-4, xn-5,…,xk的顺序，按式(25)的级联方式逐步级联，得到的n=k元布尔函数为

且显然fk1(x)和fk2(x)均为n-2=k-2阶相关免疫函数。

则当n=k+1时，按式(25)的级联方式，对fk1(x)和fk2(x) 进行级联，得

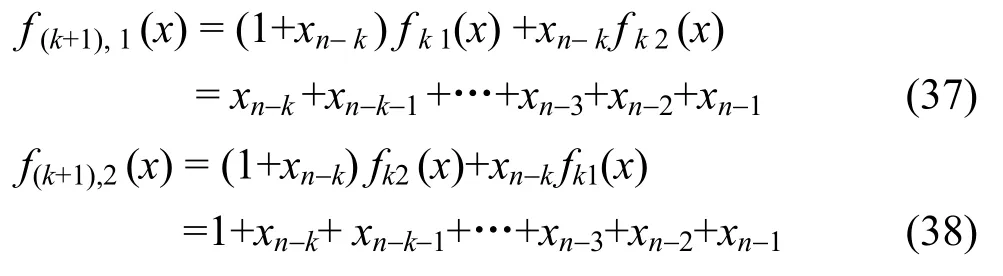
得到的仍是 k+1元线性函数（仿射函数），且显然f(k+1),1(x)和f(k+1),2(x)是n-2=(k+1)-2= k-1阶相关免疫函数。

故对于n元的，w(f(x))=w(ef(x)/exn)=2n-1的布尔函数f(x)中，存在m=n-2阶相关免疫函数。

除由上面 f21(x)和 f22(x)逐步级联构成的w(f(x))=w(ef(x)/exn)=2n-1的函数 f(x)外，尚可由(x)=0和(x)=1构成的级联函数 f '(x)，由级联式(25)可知， f '(x)一定少含变量xn-2，xn-1，xn3个，由于上面的函数是按二阶相关免疫来构造的，还必须满足 w(f(x))=w(ef (x)/exn)=2n-1，所以显然再不可能构造出其他结构的二阶相关免疫函数了。故相关免疫阶数一定小于m=n-2。限于篇幅，不详证。故知，相关免疫阶数最高为m=n-2。

由推论2和定理4，显然可得到下面的定理6 。

定理6 在w(f(x))=2n-1+2n-2的H布尔函数中，存在任意m (1≤m≤n-2) 阶相关免疫H布尔函数。

证明 设 f(x)是 w(f(x))=2n-1+2n-2的 H 布尔函数，则显然f (x)可由f1(x)=xn-1+ xn+xn-1xn；f2(x)=1+xn-1+xn-1xn；f3(x)=1+xn-1xn；f4(x)=1 +xn+xn-1xn这4个二元布尔函数逐步级联构成。这在定理3中已经看到过。由引理2的2)，有

其中，fd(x)= f(x) df(x)/dxn；fe(x)=ef(x)/exn，且w(fd(x))=2n-2，w(fe(x))=w(ef(x)/exn)=2n-1。显然，使 fe(x)=ef(x)/exn（w(fe(x))=w(ef(x)/exn)=2n-1）满足定理5的式(28)、式(29)的f(x)是存在的，并且是易于由定理 3 中的 f1(x)、f2(x)、f3(x)、f4(x)按式(25)级联构造的。故由定理4知，可以构造fe(x)是任意m (1≤m≤n-2) 阶相关免疫函数。即有

其中，1≤w(ω)≤n-2=m，ω∈GF(2)n。故知有

于是，必有

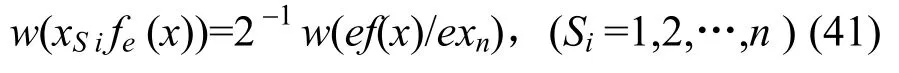
又有 w((xSi+xSj)ef(x)/exn)=w(xSief(x)/exn)+w(xSjef(x)/exn)-2w(xSixSjef(x)/exn)=2-1w(ef(x)/exn)，故由式(41)知，必有

继续这一推导，且由于又有

故由式(43)知，当fe(x) = ef(x)/exn为m (1≤m≤n-2) 阶相关免疫函数时，必有

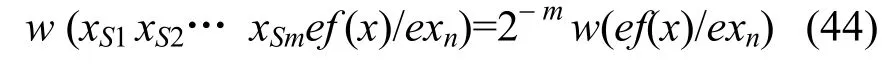
其中，1≤S1＜S2＜…＜ Sm≤n。

由于fe(x)=ef(x)/exn是满足定理5的式(28)、式(29)的要求，按定理5的方式构造的，故fe(x)必如定理5中式(37)、式(38)的形式的如下函数：

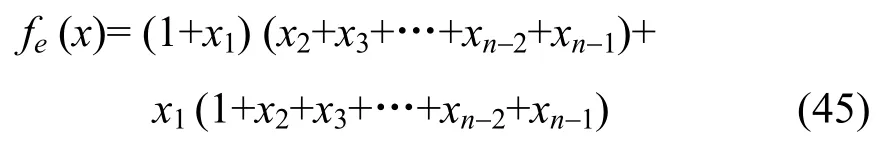
故显然有

故由式(44)、式(46)，知，必有

于是由式(47)，f (x)的构成及推论2知，f (x)是w(f(x))=2n-1+2n-2的H布尔函数中的任意m (1≤m≤n-2)阶相关免疫函数，证毕。

定理7 在w(f(x))=2n-2的H布尔函数中，存在任意m (1≤m≤n-2) 阶相关免疫H布尔函数。

证明 设g(x)为w(g(x))=2n-1+2n-2的m (1≤m≤n-2)阶相关免疫的H布尔函数。则由相关免疫的定义知，对ωx(1≤w(ω)≤m, 1≤m≤n-2)，有w(g(x)+ωx)=2n-1。取 f(x)=1+g(x)，有

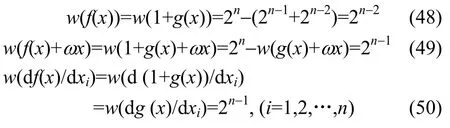
故由式(48)、式(49)、式(50)知，f(x)是 w(f(x))=2n-2的任意m (1≤m≤n-2) 阶相关免疫的H布尔函数。证毕。

现在来讨论 2n-2＜w(f(x))＜2n-1+2n-2中 H 布尔函数的相关免疫性。

定理 8 在 w(f(x))=w(ef(x)/exn)＜2n-1（即 f(x) =ef(x)/exn, df(x)/dxn=0）的布尔函数中，不存在二阶相关免疫函数。

证明 由于定理条件有f(x)=ef(x)/exn，可知f (x)必由f10(xn-1xn) =xn-1, f20(xn-1xn)=1+xn-1,f30(xn-1xn)=0,f40(xn-1xn)=1按式(6)、式(25)，即定理5中的级联方式逐步级联构成。由定理1、定理2及其推理可知，若f10(xn-1xn) 与 f20(xn-1xn) 成对出现，f30(xn-1xn)和f40(xn-1xn) 成对出现，其余均取0级联时，f(x)必为一阶相关免疫函数。由于w(f(x))=w(ef(x)/exn)＜2n-1，因而级联时要有较多的 0值二元函数参与级联。于是 f(x)必为如下形式：

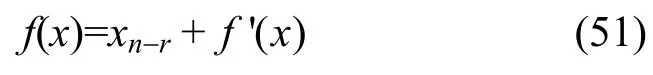
其中，xn-r是xi( i =1,2,…,n-1 ) 中的某一个， f '(x)中既含有xi( i =1,2,…,n-1 ) 中除xn-r外的其余某些一次函数项，也含有不包括xn的一些二次及二次以上的函数项（其实，一定含有xn-1这一项，只是为了一般性的考虑，以xn-r来进行标记）。以上所述的结果，只需做一些维数n较小的级联即可明显得出，然后通过归纳法即可轻易证明。由于结果很明显，限于篇幅，不再详证。由于 f(x)一阶相关免疫，故由相关免疫的定义及式(51)知，必有

现在来讨论f(x)是否二阶相关免疫。由式(51)，并经简单的重量公式推导，有

由式(53)知，w( '()fx) =2n-1，故w(xixn-r'()fx)≤2n-2，又显然 0＜2w(xn-rf (x))＜2n-1，故代入式(54)知，式(54)必不等于 2n-1，故由二阶相关免疫的定义知，f(x)一定不是二阶相关免疫函数。

推论 3 若 f(x)=ef(x)/exn（即 df(x)/dxn=0）且w(f (x))= w(ef(x)/exn)＜2n-2，则 f(x)中存在一阶相关免疫函数，但f(x)一定不是二阶相关免疫函数。

由式(2)，对 f(x)，若记 f10(x) = f (x)df(x)/dxn，f20(x)= ef(x)/exn，则

由式(55)对 f (x)分解后，下面来证明重要的定理9。

定理9 将H布尔函数f(x)分解成式(55)的f10(x)= f(x)df(x)/dxn和 f20(x) = ef(x)/exn，则 f(x)一阶相关免疫，则f10(x)和f20(x) 均必为一阶相关免疫函数；f(x)二阶相关免疫，则f10(x)和f20(x)均必为二阶相关免疫函数。

证明 同式(10)、式(11)、式(12)的推导相同，也有结果：f(x)一阶相关免疫，当且仅当

显然，若H布尔函数f (x)满足

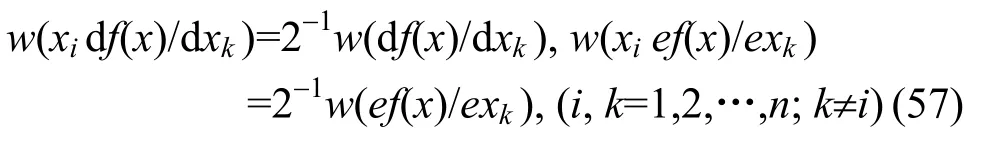
时，f(x)必满足式(56)，则f(x)必为一阶相关免疫函数。

反之，当f(x)为一阶相关免疫的H布尔函数，且w(ef(x)/exk)＜2n-1时，用反证法，假设式(57)不成立，不妨设w(xidf(x)/dxk)=2-1w(df(x)/dxk)+2n-r, 则由于f(x)为H布尔函数，有w(df(x)/dxk)=2n-1，故必有w(xief(x)/exk)=2-1w(ef(x)/exk) -2×2n-r（这一结果对n=4时是显然的。对任意的n时，用归纳法是易于证明的。限于篇幅，不再详证）。将这一结果代入式(56)左端，有

即式(56)不成立，f (x)不是一阶相关免疫H布尔函数，与f(x)是一阶相关免疫H布尔函数矛盾，故必有式(57)成立。

由于 f(x)一阶相关免疫，必有 w(xnf(x)) =2-1w(f(x))，又由式(2)，必有

同式(57)必成立的证明相同，也必有

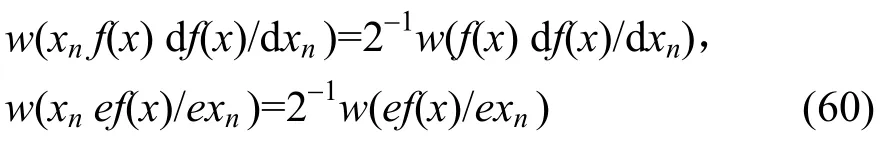
对式(57)，显然也有：f (x)一阶相关免疫，则必有

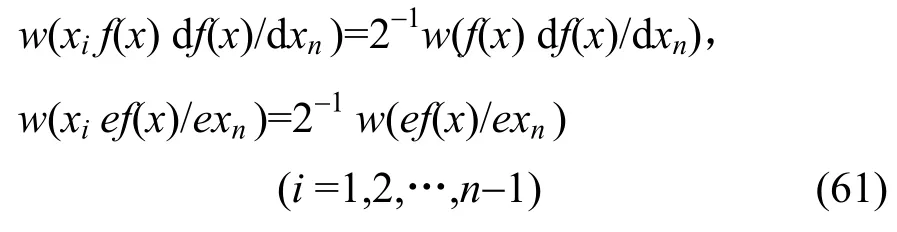
故由式(60)、式(61)知，f (x)一阶相关免疫，必有f10(x)和f20(x)均为一阶相关免疫函数。

在 2n-2＜w(f(x))＜2n-1+2n-2范围中，也普遍存在一阶相关免疫的H布尔函数，而且由定理1、定理2及其级联构造方法(6)知，一阶相关免疫的H布尔函数不仅存在，而且是易于构造的。于是，现在来讨论一阶相关免疫的 H布尔函数的二阶相关免疫性。有了前面对一阶相关免疫性的必要条件的讨论，对二阶相关免疫性的讨论，由于与一阶相关免疫相仿，和定理3已有的对w(f(x))=2n-1+2n-2的H布尔函数的讨论相同，已很显然。限于篇幅，这里只做简略的讨论。和定理 3中式(19)的讨论相同，对任意的一阶相关免疫H布尔函数f (x)，根据参考文献[4]的 p19、p133和参考文献[1]的 p39、p40、p50的定义：

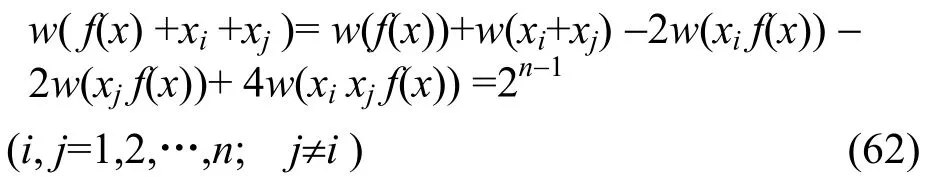
同定理3的推导相同，也有：f (x) 二阶相关免疫，当且仅当

和式(57)的讨论相同，f (x) 二阶相关免疫，当且仅当

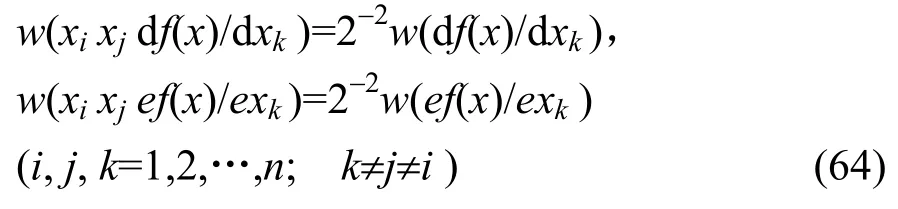
和式(60)、式(61)的讨论相同，f (x) 二阶相关免疫，也必有

即f(x) 二阶相关免疫，则f10(x)和f20(x)也必为二阶相关免疫函数。证毕。

由定理8及推论3和定理9，显然可直接得到定理10。

定理 10 在 2n-2＜w(f(x))＜2n-1+2n-2中的 H 布尔函数中，不存在二阶相关免疫的H布尔函数。

显然，这时有 w(f20(x))=w(ef(x)/exn)＜2n-1，f20(x)不是二阶相关免疫的，则再由定理9即得出结论。但由于结论很重要，故作为定理给出。

4 结束语

H布尔函数存在于一个很大的重量范围内，数量庞大[10]。H布尔函数的相关免疫性及其阶数与重量有无联系？有何联系？m阶相关免疫的H布尔函数的相关免疫阶数m与它的维数n有无关系？有何关系？本文对这些问题进行解决，给出了具体的结果，即只有在 w(f(x))=2n-1+2n-2和 w(f(x))=2n-2的 H布尔函数中，存在任意 m(m≥1) 阶相关免疫的 H布尔函数，m和维数n的关系为max mi=n-2。而在2n-2＜w(f(x))＜2n-1+2n-2这样一个大范围内的各种重量的H布尔函数中，只存在一阶相关免疫的H布尔函数，但不存在二阶相关免疫的H布尔函数。这些结果使 H布尔函数的相关免疫性和重量明确联系起来，能够按重量进行分类，这对构造具有良好密码学性质的布尔函数有实际意义，由此也可知，H布尔函数在密码学研究中有重要作用。

参考文献：

[1] 李世取,曾本胜, 廉玉忠等. 密码学中的逻辑函数[M].北京: 北京中软电子出版社,2003.LI S Q, ZENG B S, LIAN Y Z, et al. Logic Function in Cryptography[M]. Beijing: Beijing Soft Electronic Publishing House, 2003.

[2] 杨义先. N元H布尔函数[J]. 北京邮电大学学报,1988,11(3):1-9.YANG Y X. On the H-Boolean functions[J]. Journal of Beijing University of Posts and Telecommunications, 1988,11(3):1-9.

[3] 杨义先,邢育森. N元H布尔函数(Ⅱ)[J].电子科学学刊,1997, 19(2):214-216.YANG Y X,XING Y S. On the H Boolean function(Ⅱ)[J]. Journal of Electronics,1997,19(2): 214-216.

[4] 温巧燕,钮心忻,杨义先. 现代密码学中的布尔函数[M].北京:科学出版社,2000.WEN Q Y, NIU X X, YANG Y X. Boolean Function in Modern Cryptoloy[M]. Beijing: Science Publishing House, 2000.

[5] LI W W, WANG Z. The e-derivative of boolean functions and its application in the fault detection and cryptographic system[A]. The 5th IIGSS Workshop, Kybernetes[C]. 2007. 245-249.

[6] 何亮, 王卓, 李卫卫. 减小平衡H布尔函数相关度的算法和相关问题研究[J]. 通信学报, 2010,31(2):93-99.HE L, WANG Z, LI W W. Algorithm of reducing the balanced H-Boolean function correlation_measure and research on correlation issue[J]. Journal on Communications, 2010, 31(2): 93-99.

[7] DING Y J, WANG Z, YE J H. Initial-value problem of the Boolean function's primary function and its application in cryptographic system[J]. Kybernetes, 2010, 39(6): 900-906.

[8] XIAO G Z, MASSEY J L. A spectral characterization of correlation-immune combining functions[A]. IEEE Trans on Inform[C]. 1988.

[9] 温巧燕, 张劼, 钮心忻等. 现代密码学中的布尔函数研究综述[J].电信科学, 2004,20(12):43-46.WEN Q Y, ZHANG J, NIU X X, et al. Review of Boolean functions of modern cryptography[J]. Telecommunication Science, 2004, 20(12): 43-46.

[10] DELFS H, KNEBL H. Introduction to Cryptography[M]. Springer-Verlag, 2002.