无线传感器网络的轻量级安全体系研究

王潮，胡广跃，张焕国

（1. 上海大学 特种光纤与光接入网省部共建重点实验室, 上海 200072；2. 空天信息安全与可信计算教育部重点实验室，湖北 武汉 430072；3. 武汉大学 计算机学院，湖北 武汉 430072）

1 引言

无线传感器网络（WSN, wireless sensor network）由大量节点以自组织的方式组成，网络中没有中心控制节点，较远距离节点间以多跳的方式进行通信。由于无线传感器网络无需预先部署基础设施，在战场环境、抢险救灾、环境威胁探索等领域具有广泛的应用前景[1]。安全、高效是这些应用对自组织网络提出的最基本要求。

无线传感器网络中的安全威胁主要有以下6个方面[2]。

1) 多跳共享的无线信道。无线传感器网络中，以无线信号作为传输媒介，信息在无线信道传输，任何具有无线接收装置的人都可以窃听。另外，无线传感器网络采用多跳通信，与传统移动通信的单跳通信相比，节点的身份不仅仅需要像基站这样的集中控制设备进行认证，而且需要其周围的邻居节点进行认证，传统的安全措施无法在无线传感器网络中有效地应用。

2) 节点的移动性。无线传感器网络中，节点处于不同的区域(可能是安全区域，也可能是非安全区域)自由移动，无法保证网络的物理安全，尤其在战场环境中，节点在移动的过程中随时可能被敌方俘获，造成节点内的秘密信息可能泄露，造成严重的安全威胁；这些被俘获的节点被敌军利用，可能会重新加入网络，用来获取更多的秘密信息。因而，在无线传感器网络中，防范内部攻击和外部入侵同样重要。

3) 动态的网络。节点的移动带来网络拓扑也经常处于变化之中，动态变化的网络拓扑容易造成路由的不正常中断，带来网络上节点的重认证请求，因而需要高效的认证措施。

4) 无中心和无基础设施。传统网络中，通过基础设施的支持，采用PKI或CA认证等方式，可以有效地运行大多数安全服务，而在无线传感器网络中，无法提供一个全网信任的权威机构或认证中心来完成安全认证、密钥管理等工作，而且，即使网络中存在这样的中心节点，也无法保证能提供实时在线的服务。另外，单一的认证中心容易成为系统的单一失效点，一旦崩溃将导致整个网络无法工作，并造成密钥等敏感信息的泄露。

5) 信任机制。现有无线传感器网络的大多数协议，如路由、邻居发现等都假定网络中所有的节点是乐于提供服务的，通过节点之间的相互合作，从而共同完成信息的传递。然而，网络中节点有可能由于诸多的原因而不提供转发数据服务，节点的自私行为会导致网络性能下降，另外，由于没有集中管理机构对所有节点进行管理，节点间很难建立一种相互信任的机制，采用完全信任的方式将导致泛洪攻击和拒绝服务等攻击，使得网络性能急剧下降。

6) 多播安全。在无线传感器网络中，路由信息、簇算法、邻居发现、机密通信等都需要多播通信支持，这些多播的数据多是机密或敏感的信息，如何保证多播数据分组的机密性、完整性和不可抵赖性，实现安全多播，是无线传感器网络多播必须解决的问题。

无线传感器网络的特点决定无线传感器网络的安全威胁、安全体系和安全算法与传统网络大相径庭，不能照搬传统网络的安全体系和安全算法。同时，无线传感器网络有限的存储空间和计算能力以及有限的带宽和通信能量等自身特点，也决定了传统的基于密码技术的计算量较大的数据加密及公钥密码体制等网络安全技术不太适应于无线传感器网络。本文将主要讨论无线传感器网络相关的安全体系和安全算法设计。

2 研究现状

目前，一些无线传感器网络安全方案存在密钥管理效率低、缺乏组网安全和对节点的认证（双向认证）、认证效率低、密码算法复杂度高未达到轻量化等问题，不适合无线传感器网络资源有限等特点。

Ibriq和Mahgoub[3]提出了一种高效的层次密钥模型，在该方案中，一个sink节点可以为连接的节点产生共享密钥，然而，一些sink节点必须在表中保留每个节点的信息来支持节点的移动。Fantacci等[4]提出了分布式节点认证模型，该方案不需要基站作为认证的中心。该方案中，每个节点共享部分认证信息。当一个节点请求被另一个节点认证时，节点2作为认证器，其他节点（如节点5和节点6）作为分布式认证服务器。该方案需要大量的节点参与，使得开销分布在每个节点上。因为节点必须作为认证过程的参与者或者一个认证服务器，那么计算和通信的开销将会随着认证请求的频繁而不断增大。Han等[5,6]提出的方案，能够提高认证的效率，然而针对节点的初始化认证过程中却仍然离不开第三方的参与，认证效率低，通信开销也较大。

3 无线传感器网络的轻量级安全体系设计

在无线传感器网络中，由sink节点组成了无线传感器网络的骨干网。在无线传感器网络环境中，为了防止恶意节点攻击，在骨干网中，系统的主密钥也不能单独保存在某个节点，以防止单点失效以及恶意节点攻击问题的发生。本文基于门限思想进行骨干网的组网，由多个簇头节点掌握系统的主密钥s的秘密份额，利用门限秘密共享机制建立安全可靠的骨干网络。

当普通节点接入骨干网进行通信时，本文基于ECC的CPK体制的思想[7]，降低密钥管理的存储、通信和计算等开销，并进行双向认证[8]，防止恶意节点的攻击。采用轻量化的点乘运算减少计算开销的ECC算法[9]，优化双向认证过程进一步减少通信和计算的开销。

3.1 基于ECC的CPK体制思想

基于ECC的组合公钥（CPK）密码体制[7]认证方式是基于标识的身份认证。它依据椭圆曲线离散对数的数学原理构建公钥矩阵与私钥矩阵，采用散列函数将实体的标识映射为矩阵的行与列坐标序列，用以对矩阵元素进行选取与组合，可以生成数量庞大的公私钥对，从而实现基于标识的大规模密钥生产与分发。实体节点只要知道对方节点的标识，就可以计算其公钥，从而可以方便地实现认证和保密功能。其中，标识密钥(identity key)由实体的标识通过组合矩阵生成。采用基于ECC的CPK体制，有以下的优势。

1) 在无线传感器网络中，只有合法的节点具有组合私钥，而且可以根据对方的标识 ID以及分割密钥，计算出对方的组合公钥CPK，所以在无需第三方的参与下，即可实现简单高效的认证过程。

2) 基于ECC的CPK体制可以通过少量的公/私钥矩阵，组合出规模庞大的公/私钥对，节点仅需要存储很小的矩阵，就可实现网络中大量节点的安全认证。

采用基于ECC的CPK体制，密钥的安全性依赖于椭圆曲线离散对数求解困难性，是指数级破译难度。攻击者想通过公钥获得私钥，基于椭圆曲线离散对数问题的困难是不可行的。

点乘运算是CPK算法的基础。ECC签名算法(ECDSA)是数字签名算法(DSA)的椭圆曲线版本，同时也是 CPK数字签名算法的基础。本文采用基于 Montgomery型曲线的椭圆曲线密码算法[9]，为解决 ECC点乘计算量大等问题，采用如下轻量级的Montgomery型椭圆曲线的点乘运算，方案采用二进制移位 NAF编码算法，在射影坐标下避免大部分模逆算法，采用未计算y值的点加和倍点快速运算。

点加公式如下：

计算点P=(x,y)的倍点dP在射影坐标下的坐标(X,Z),具体的算法如下：

2) 计算整数：

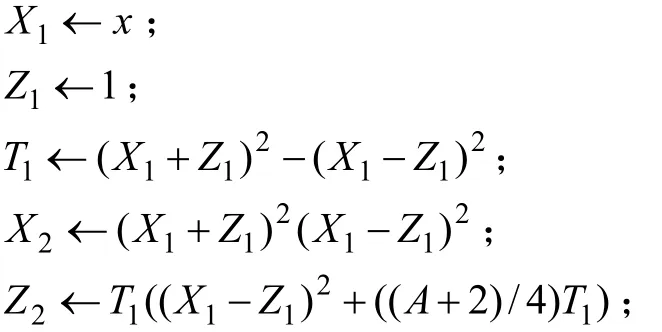
3) 如果 0=i ，则跳到12)，否则执行4)；

4) 1-←ii；

5) 如果 di=0，则执行6)，否则跳到9)；

6) 计算整数：

7) 计算整数：

8) 跳到 3)；

9) 计算整数：

10) 计算整数：

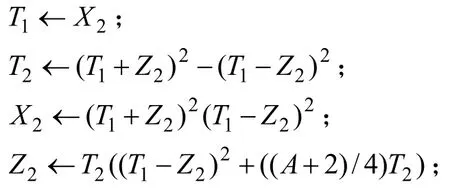
11) 跳到3)；

12) 输出整数X1,Z1，作为dP相应的X,Z。

计算出上面算法的复杂度为(6|d|-3)M+(4|d|-2)S，这里的表示转化成二进制时的长度lbd。

3.2 系统的建立

在网络部署前，密码管理中心（KMC）选定散列函数、椭圆曲线参数信息、公/私钥矩阵等信息，由密码管理中心进行节点的标识、密钥参数和各个节点证书的产生和分发，这样每个节点都拥有了自己的标识（ID）、分割密钥（SPK）、组合私钥（CSK）、组合公钥矩阵PSK、证书以及椭圆曲线参数等信息。下面介绍本文具体方案的实现。

3.2.1 簇头节点组网及其密钥的建立

第1步 系统密钥对的生成

为了防止单个簇头节点失效和恶意簇头节点攻击等问题，由该网络中的簇头节点共举产生主密钥。下面描述其实现过程：

对于身份标识为IDi的节点i，随机选择si作为主密钥s的秘密份额和系数ai,j(j∈1,2,…,k -1)以建立(n,k)门限多项式fi(x)：

用节点i计算式(7)，通过安全信道发送给相应的节点j。此外为了使节点j验证si的有效性，节点i计算V0=siP及Vi=ai,jP( j∈1,2,…,k -1)传送给节点j。

节点j收到fi(j)、V0和Vi后，验证fi(j)≡V0+，如果成立则验证通过，消息为节点i所发，否则断定消息并非节点i发送。

节点j收到来自网络中的n个节点所发送的门限多项式，计算fj(j)，共举可以得出网络的主密钥s：

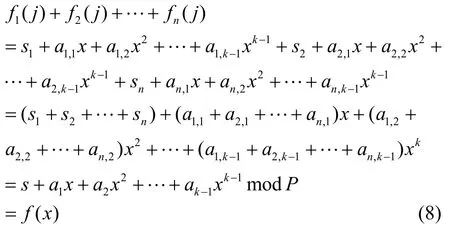
计算Ppub=sP，由此得出系统的密钥对(s, Ppub)。

第2步 通信组密钥的建立

当簇头节点i进行通信前，需要用通信的加密信息对保障信息传输的安全性。在簇头节点共举出主密钥后，某个节点i需要申请会话密钥的时候，可以通过向掌握系统秘密份额的簇头节点查询来获取。

要实现这一过程，首先需要验证节点i的有效性，即它是否为网络的合法节点，以防止恶意节点的加入。具体的验证过程如下。

1) 申请会话密钥的节点i与掌握秘密份额的节点j进行通信，随机选择ri∈作为私钥，并计算Qi=riP作为相应的公钥发送给节点j。

2) 节点j接收到节点i的请求后，需要验证节点i的身份。节点j是合法的节点，它拥有加密密钥对(SKj,PKj)，它随机选择信息m，发送r=(m,PKj)给节点i，等待后者的签名。

3) 节点i收到签名要求后，随机选择ti∈，其对应公钥为ui=tiH2(IDi)。计算身份签名，把(ui,σ)传送给节点j。

4) 节点j收到节点i的签名后，进行签名认证。如果e(P,P)=e(H2(IDi)P +tiP,σ)，则节点j接受节点i的签名，把它认为是合法节点，不然则拒绝其签名。

为了提高系统的安全性和健壮性，对于应答节点j发送的秘密份额，请求节点i同样验证其签名，检查其合法性，实现双向认证，其具体过程如下。

1) 节点j计算发送的密钥份额：sjH2(seed)，同时随机选择tj∈，其对应公钥为uj=tjH2(IDj)。计算身份签名σ=[H2(IDj)+tj]-1P，把(uj,σ,sjH(seed))传送给节点i。

2) 节点i收到签名后进行签名认证。如果e(P, P)=e(H2(IDj) P+tjP,σ)，则节点i接受节点j的签名，不然则拒绝其签名。验证身份后，节点i即可得到加密密钥的份额sjH2(seed)。

3) 同理，节点i与其他掌握秘密份额的节点通信，当节点i获得k个密钥份额后，依据Lagrange插值原理获得完整的通信组密钥：

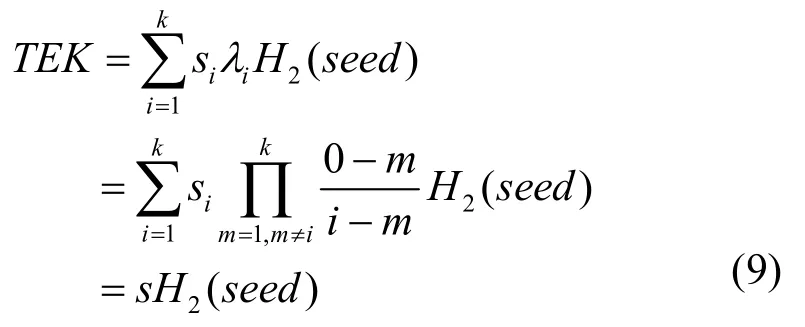
3.2.2 普通节点与其他节点的双向认证和密钥协商

密钥协商方案就是一种能够让通信的双方或者多个参与方在一个公开的、不安全的信道上通过密钥协商联合建立一次会话所用的临时密钥的密码协议。

为了有效地抵御中间人攻击及弥补这个显著的缺陷，本文采用一种利用可信第三方颁发的证书以及产生随机数增加临时密钥的算法来完成双向认证和密钥协商[8]。

以A和B之间的认证为例，假设在算法执行前，已经完成了合法节点证书的发放，具体参数设定为：Ad为A的私钥，AQ为A的公钥，Bd为B的私钥，BQ为B的公钥，Acert为A的证书，Bcert为B的证书。步骤如下：

1) A随机产生一个数r1，计算TEP1=(dA-r1)·G，发送给B：TEP1，QA；

2) B随机产生一个数r2，计算TEP2=dB·TEP1，TEP3=r2·G，发送给A：TEP2，QB，TEP3；

3) A收到相应的信息，A计算TEP4=dA·TEP3，TEP5=dB·TEP1+r1· QB，h1=h( TEP4, TEP5, cert A)，发送给B：certA，h1；

4) B收到相应的信息，首先验证certA，若不成功，返回错误信息，要求重发，否则计算TEP6=r2·QA，TEP7=dB·QA，TEP8=(dB-r2)·G ，比较h2=h( TEP6, TEP7, certA)和h1是否相等，若验证成功，继续执行。发送给A参数为：E(certB,TEP8)，这里已经产生会话密钥dBdA·G，E表示用会话密钥进行的加密；

5) A收到相应的信息，首先解密E(certB,TEP8)，验证certB，同时计算TEP9=dA·TEP8+dA·TEP3是否与TEP10=dA·QB相等，若成功，则认证成功，同时完成密钥协商，会话密钥为：dBdA·G。

4 性能分析

4.1 安全性分析

本文采用基于ECC的CPK体制，其安全性是基于椭圆曲线离散对数问题，是国际上公认的安全实用的密码体制。椭圆曲线的离散对数问题(ECDLP)的计算困难性在计算复杂度上目前是完全指数级，攻击者想通过公钥破译私钥是不可行的，可以满足无线传感器网络的安全要求。本文提出的双向认证的方法还可以抵御中间人攻击。

4.2 计算开销

文中在节点的认证以及重认证过程中，反复用到了加解密运算以及数字签名算法，其中标量乘运算是主要的计算开销，本文采用了基于Montgomery型轻量级的快速点乘运算，计算复杂度为，与目前其他典型方案的计算量的对比如表1所示，相对于其他的算法具有更少的计算复杂度（表1中M表示乘法，S表示平方，I表示求逆，n表示dP点乘运算中d的二进制位数）。

表1 计算复杂度对比

方案中双向认证（3.2.2节）的计算复杂度分析如下：

第1步的计算复杂度为TM+；

第2步的计算复杂度为2TM；

第3步的计算复杂度为3TM+TA+Th；

第5步的计算复杂度为3TM+TA+。

所以，总的计算复杂度为11TM++2TA+。其中，TM表示计算ECC曲线点积所使用的时间，TA表示计算ECC曲线点加所使用的时间，表示计算模减所使用的时间，Th表示散列函数所使用的时间，表示证书验证所使用的时间。

通过算法计算复杂度的分析，计算耗时最多的点积运算显著减少，即在密钥协商算法过程中，其点积运算仅为11次运算，而另一耗时比较多的证书认证计算仅为2次。同时在此算法中，使用了散列函数，大大减少了交换的信息量，进一步提高了算法速度。

4.3 存储开销

本文采用基于ECC的CPK体制思想：可以由规模很小的矩阵组合出很大数量的公/私钥对，以达到规模化的密钥管理。簇头节点需要预存椭圆曲线公钥矩阵信息，无需预存大量密钥信息，节约存储空间。对于普通节点仅需要保存自己的公/私钥对，其他节点的公钥可通过查询公钥矩阵，再对公钥因子进行点加运算就可得到该用户的公钥。

5 结束语

无线传感器网络的特点决定了其安全威胁、安全体系和算法等与传统电信网络截然不同。

本文结合无线传感器网络的特点，提出了无线传感器网络的轻量级安全体系，基于门限秘密共享机制的思想解决了无线传感器网络组网中遭遇恶意节点的问题；采用双向认证的方式保证普通节点与簇头节点间的通信安全，认证过程简单高效，使用轻量化 ECC算法设计，减少认证过程中的计算开销和通信开销；优化基于ECC的CPK体制的思想，可实现高效的认证过程，安全性依赖于椭圆离散对数分解的指数级破译计算复杂度；使得密钥管理适应无线传感器网络的资源受限等要求。

[1] GERLA M. Ad Hoc Networks: Technologies and Protocols[M].Springer Science Press,2004.

[2] 王潮, 张振华, 应仲平. WSN中基于身份的分散密钥管理研究[A].第六届中国测试学术会议论文集[C]. 2010.WANG C, ZHANG Z H, YING Z P. Research on distributed key management based on identity in wireless sensor networks[A].CTC2010[C]. 2010.

[3] IBRIQ J, MAHGOUB I. A hierarchical key establishment scheme for wireless sensor networks[C]. AINA’07[C]. Niagara Falls, Canada,2007. 210-219.

[4] FANTACCI R, CHITI F, MACCARI L. Fast distributed bi-directional authentication for wireless sensor networks [J]. Security and Communication Networks, 2008, 1(1): 17-24.

[5] HAN K, SHON T, KIM K. Efficient mobile sensor authentication in smart home and WPAN [J]. IEEE Transactions on Consumer Electronics, 2010, 56(2): 591-596.

[6] HAN K, KIM K, SHON T. Untraceable mobile node authentication in WSN[J]. Sensors, 2010, 10(5): 4410-4429.

[7] 南湘浩. 组合公钥(CPK)体制标准(v5.0)[J]. 计算机安全,2010,(10):1-2.NAN X H. CPK-cryptosystem standard (v5.0)[J]. Computer security,2010,(10):1-2.

[8] 王潮, 朱美丽, 时向勇. 基于ECC的CBTC无线接入安全认证架构研究[J]. 哈尔滨工业大学学报（增刊）, 2009, 41(1):193-197 WANG C, ZHU M L, SHI X Y. Research of structure of secure authentication based on ECC for wireless CBTC[J]. Harbin Journal of Harbin Institute of Technology, 2009, 41(1): 193-197.

[9] 王潮, 时向勇, 牛志华. 基于 Montgomery 曲线改进 ECDSA算法的研究[J]. 通信学报, 2010,31(1):9-13.WANG C, SHI X Y, NIV Z H. The research of the promotion for ECDSA algorithm based on Montgomery-form ECC[J]. Journal on Communications, 2010, 31(1):9-13.

[10] OKEYA K, SAKURAI K. A scalar multiplication algorithm with recovery of y-coordinate on the Montgomery form and analysis of efficiency for elliptic curve cryptosystem[J]. IEICE Trans Fundamental,2002, 85(1): 84-93.

[11] FUTA Y, OHMORI M. Efficient scalar multiplication on Montgomery-form elliptic curves[J]. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, 2004,87(8):2126- 2136.

[12] LIU D, DAI Y Q. The algorithm of computing kP+mQ+lR on a Montgomery-form elliptic curve[A]. Chinese National Conference of Computer 2003[C]. Beijing: Tsinghua University Press,2003.198-203.