大地电磁三维交错网格有限差分数值模拟的并行计算研究

李 焱，胡祥云，杨文采，魏文博，方 慧，韩 波，彭荣华

1 中国地质大学（武汉）地球物理与空间信息学院，武汉 430074

2 中国国土资源航空物探遥感中心，北京 100083

3 中国地质科学院，北京 100037

4 中国地质大学（北京）地球物理与信息技术学院，北京 100083

1 引 言

大地电磁三维数值模拟一直是国际地球内部电磁感应领域研究的前沿和热点课题.目前，大地电磁二维反演解译已用于生产实践［1－3］，三维反演仍处于研究和试验阶段［4－6］，实际资料的三维反演尚未大范围推广应用.主要原因是三维反演计算规模很大，耗费时间很长，普通的微机难以承受，而反演中绝大部分计算时间花费在正演或者与正演有关的运算上，包括模型修正量、雅可比矩阵或其与向量的乘积的计算等，因此采用并行计算来加快正演计算速度无疑具有现实意义.MPI（Message Passing Interface）是目前国内外在高性能计算机系统中最广泛使用的并行编程环境，它具有移植性好、功能强大、效率高、有多种不同的免费、高效、实用的实现版本、几乎所有的并行计算机厂商都提供对它的支持等多种优点，是目前最重要的并行编程工具［7－8］.

自20世纪70年代中期开始，已经有学者致力于三维大地电磁的正演研究［9］，目前成熟的三维正演方法主要有：有限元法［10－12］、有限差分法［13－15］、积分方程法［16－18］、有限体积法、边界元法等，其中Mackie等发展的交错网格有限差分法因迭代收敛稳定、计算精度高、能反映较复杂地电模型已成为主导的正演计算方法，众多三维反演方法均以该方法为正演核心［4，6，19－24］.但三维正演数值模拟需要求解大型稀疏对称系数矩阵线性方程组，计算量非常大，消耗的时间非常长，尤其是网格剖分较密、频点数较多时.基于此，本文开展了大地电磁三维交错网格有限差分数值模拟并行计算研究.大地电磁三维正演数值模拟是按照不同频率来计算的，各频率之间求取电磁场值的过程是相互独立的.每个频率都需要求解大型线性方程组一次，当参加计算的频率个数较多时，可以将多个频率的计算任务平均分配到不同计算节点去并行执行.基于该并行思想，本文在曙光TC－5000A高性能并行平台上，以MPI为并行编程环境，实现了大地电磁三维交错网格有限差分数值模拟的并行算法.通过对两个理论模型进行试算和分析，证明了该并行算法的正确性和高效性，为进一步大地电磁三维反演并行算法研究奠定了重要基础.

2 MPI和高性能并行平台简介

MPI是由全世界工业、科研和政府部门联合建立的一个消息传递编程标准，其目的是为基于消息传递的并行程序设计提供一个高效、可扩展、统一的编程环境.它是目前最为通用的并行编程方式，也是分布式并行系统的主要编程环境.MPI标准中定义了一组函数接口用于进程间的消息传递.编程人员通过调用MPI的库程序来编写并行程序.MPI是一种标准或规范的代表，而不特指某一个对它的具体实现，一个正确的MPI程序，可以不加修改地在所有的并行机上运行［7－8］.

MPI并行程序可分为两种基本模式，即对等模式和主从模式.对等模式是指MPI程序的各个进程的功能、地位相同或相近，MPI程序的代码也应该是相近的，所不同的只是处理的对象和操作的数据.主从模式是指MPI程序的各个进程所起的作用和地位并不相同，一个或者一些进程完成一类任务，而另外的进程完成其它的任务，这些功能或者地位不同的进程所对应的代码也有较大的差别.

本文开发的大地电磁三维交错网格有限差分数值模拟并行程序均在中国地质大学（武汉）曙光TC5000A高性能计算平台上运行.该平台采用X86刀片集群服务器架构，整套系统包括92个计算节点、2台SMP 8路计算节点、5个I／O、双作业调度系统和一台集群管理维护节点.节点间的通信连接采用20G的Infiniband连接，管理网络采用1000M以太网交换机连接，MPI层消息传递延迟小于1.5μs.SMP服务器配置128G的海量内存，每一个计算节点配置内存为16G，管理节点和作业调度节点配置16G内存、每一个I／O节点配置32G内存；整个系统内存总容量是1936G.采用业界主流的x4DDR Infiniband作为通信网络互联全部节点，点对点单向网络带宽达到线速20Gb／s；提供适用于AMD多核平台的全套编译、调试软件以及数学函数库，支持标准的Fortran／C／C＋＋编程，支持OpenMP、MPI以及OpenMP和MPI的混合并行编程.曙光TC5000A高性能计算平台功能强大、运算快捷、存储量大，完全满足本文的计算要求.

3 大地电磁三维交错网格有限差分数值模拟

在大地电磁研究的频率范围内，位移电流的作用可以忽略［25］.通常取电磁场随时间变化的因子为e－iωt，麦克斯韦方程组的积分形式如下：

其中，σ为电导率，μ为空气中的磁导率，ω为角频率，J为传导电流密度，要解上述方程组需要将连续形式的积分方程组转化成离散形式.对研究区域离散化，即把研究区域剖分成若干个小的长方体单元.假设沿x、y和z轴方向分别剖分成Nx、Ny和Nz段，网格间距分别为Δx（i）（i＝1，…，Nx）、Δy（j）（j＝1，…，Ny）和Δz（k）（k＝1，…，Nz）.长方体网格单元的6个电磁场分量的采样点位置取法为磁场H取在长方体单元棱上的中点处，电场E取在长方体单元面上的中心处，这样可以自动保证电磁场分布满足能量守恒定律.以编号为（i，j，k）的长方体网格单元为例，如图1所示.

将积分形式的麦克斯韦方程组（1）、（2）离散化后即可获得大型稀疏线性方程组：

图1 交错采样网格示意图Fig.1 Sketch of Staggered-grid

其中，b是包含源场和与已知边界条件值有关的项，x是求解域内部的未知磁场分量，A是对称的大型稀疏系数矩阵.为了保证迭代收敛稳定，对A进行不完全Cholesky分解，采用双共轭梯度法对方程（3）求解，就可以得到各网格单元采样点处所有的磁场值H，进而求得电场E.

大地电磁所用场源有两种极化模式：Ex－Hy和Ey－Hx，Ex－Hy在水平面内产生的电场和磁场分量值分别记为EX1、EY1、HX1和 HY1，Ey－Hx在水平面内产生的电场和磁场分量值分别记为EX2、EY2、HX2和HY2，通过电磁场和阻抗张量关系式可以求得三维介质的张量阻抗：

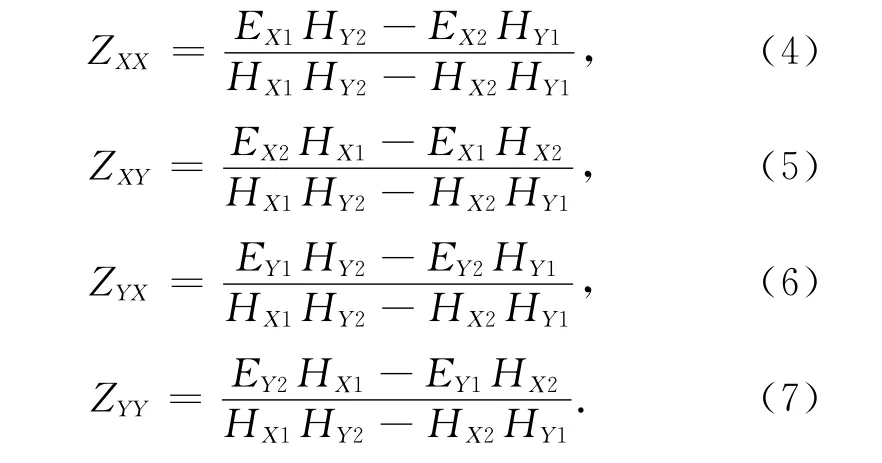
式（5）定义的响应称为XY模式响应，（6）定义的响应称为YX模式响应.按照下面公式可以求出三维介质的视电阻率和相位［25］：

4 三维正演数值模拟并行算法的总体设计

通过对三维交错网格有限差分数值模拟算法深入分析发现，三维正演计算中，频率循环部分求解电磁场值为主要计算时间，占据了整个计算时间的90%以上，是需要并行化的部分.三维正演首先将积分形式的麦克斯韦方程组离散化，然后将方程组化简去参加入边界条件值，最后求解（3）式.对于给定的不同频率值，方程组求出的磁场值是相互独立的，不同频率值相互之间对方程组没有影响，根据这一特点我们可以将串行算法按频率进行粒度划分，将每个频率对应的部分分配到不同节点上同时进行计算，并行执行.

程序采用主从并行模式，分为主进程和子进程，主进程负责维护全局的数据结构和任务的分配、参数的发送、计算结果的回收整合以及最后结果的输出，子进程从主进程处接受参数执行分配任务的计算并将结果发回主进程.由于主进程计算量不大，为了充分利用计算资源，不设置专用的控制节点，主进程同时也作为子进程参与计算.三维正演并行计算的基本思路是：启动并行环境，主进程读入所有频率值和模型网格剖分数据，将其广播给所有子进程，主从进程按照分配的频率同时各自独立的计算模型响应，待全部计算完后，子进程将计算结果发回主进程，主进程整合所有收到的结果，并将其输出，结束并行环境.图2为大地电磁三维正演并行计算简化流程图.

5 三维正演并行程序测试和计算效率分析

为了对开发的大地电磁三维正演并行算法的高效性进行验证，我们设计了两个模型在曙光TC5000A高性能计算平台上进行试算，两模型频点数均为36，频率从320Hz到0.005Hz.

5.1 模型一：3D／2D模型

如图3所示：该模型为3D／2D模型，即区域构造是2D，含有3D异常体.棱柱体大小为2km×2km×1km，电阻率为5Ωm，顶面埋深为1km，中心位于（0，－3000m，1500m），覆存于电阻率为100Ωm的二维构造中，二维走向为y方向，基底电阻率为1000Ωm.三维交错网格有限差分正演在x、y、z方向剖分网格单元数分别为Nx＝62，Ny＝56，Nz＝43.

图2 大地电磁三维正演并行计算流程图Fig.2 Flow chart of 3DMT forward modeling parallel computation

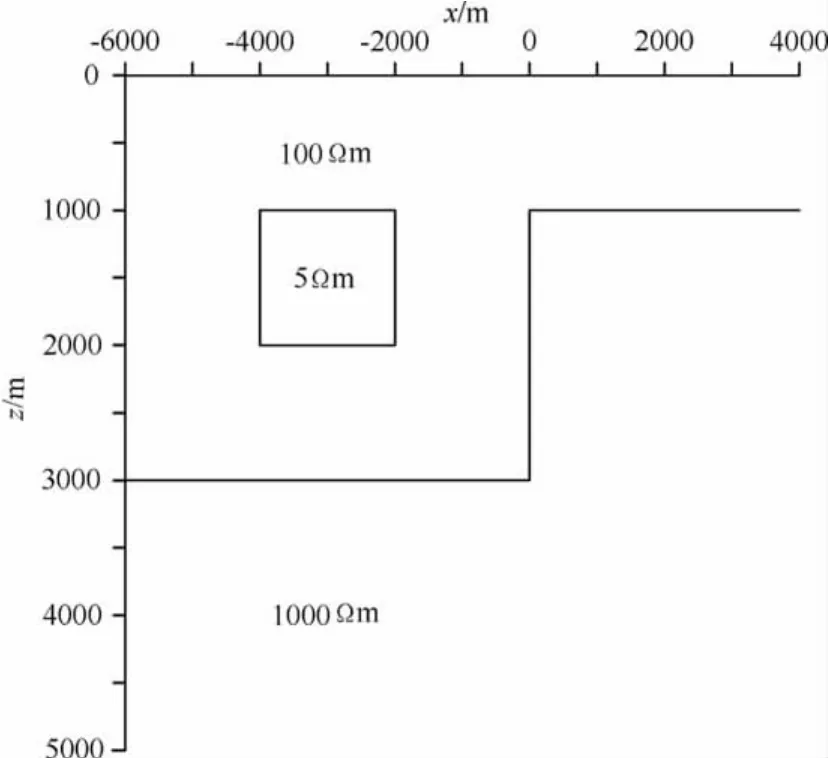
图3 模型在y＝－1～1km间垂直方向断面图Fig.3 Vertical section of model at y＝－1～1km

图4和图5是3D／2D模型视电阻率和相位4种模式在剖面y＝0时沿x轴方向的响应拟断面图.在XY模式和YX模式视电阻率拟断面图上，3D／2D模型的YX模式较好的反映出三维棱柱体的形态和范围，特别是埋深和底界面，而XY模式反映的三维棱柱体明显向下拉伸.XY模式和YX模式相位拟断面图都较好的反映出三维棱柱体的形态和范围，其中XY模式横向分辨率比YX模式横向分辨率高，两种模式对2D构造及基底形态反映不明显.从XX模式和YY模式视电阻率拟断面图上可以看出两种模式的视电阻率值都非常小，不能反映模型的形态.因为XX模式和YY模式视电阻率值都非常小，再加上正演模拟过程中解方程时所给定的收敛判别标准误差，因此XX模式和YY模式的相位信息是不可靠的，也无法反映模型的形态.从这里还可以看出阻抗信息非对角元素的作用远大于对角元素的作用.

5.2 模型二：低阻体和高阻体组合模型

设计的第二个模型如图6所示：高阻三维棱柱体电阻率为1000Ωm，低阻三维棱柱体电阻率为10Ωm，它们大小相同，均为2km×2km×1km，顶面埋深为0.5km，中心分别为（3km，0，1km）和（－3km，0，1km）围岩电阻率为100Ωm.三维交错网格有限差分正演在x、y、z方向剖分网格单元数分别为Nx＝64，Ny＝44，Nz＝41.

图6 低阻体和高阻体组合模型（a）模型在y＝－1km～1km处垂直方向断面图；（b）模型在z＝0.5km～1.5km间平面俯视图.Fig.6 Low resistance and high resistance（a）Vertical section of model at y＝－1～1km；（b）Flat section of model at z＝0.5～1.5km.

图7和图8是高阻体和低阻体组合模型的视电阻率和相位两种模式响应拟断面图.由于XX模式和YY模式的信息不能较好的反映出异常体，这里只给出XY模式和YX模式的响应拟断面图.在XY模式和YX模式视电阻率拟断面图上，较好的反映低阻体和高阻体，相比较而言右边的高阻体响应不如左边的低阻体明显.两种模式的视电阻率拟断面图都较好的反映了异常体的顶深和横向范围，其中XY模式比YX模式在横向范围上反映更准确一些，YX模式在横向上有一定延伸.两种模式的相位响应拟断面图均能较好的反映出低阻体和高阻体的整个范围，尤其是能反映视电阻率无法反映的底界面.

5.3 并行程序正确性的验证

由于本文的并行计算完全是在原有串行算法上实现的，只是在相应处增加了并行处理部分，即MPI处理语句和函数调用，对算法本身未做任何修改，因此，计算结果应该和串行计算结果一致，这是检验并行程序设计正确性的标准.图9是3D／2D模型中串行计算和并行计算在异常体上方一测点上的XY模式视电阻率频率图，从图中可以看出两曲线完全重合，从而验证了并行程序是正确的.

5.4 并行效率分析

为了检验开发的三维正演并行程序的效率，采取不同的节点数来计算模型一和模型二，并通过并行加速比和并行效率来评价并行算法的效果.并行加速比＝单机串行算法的执行时间／N个进程并行算法的执行时间；并行效率＝并行加速比／参加并行计算的进程个数.表1是3D／2D模型正演测试时间统计表；表2是低阻体高阻体组合模型正演测试时间统计表.

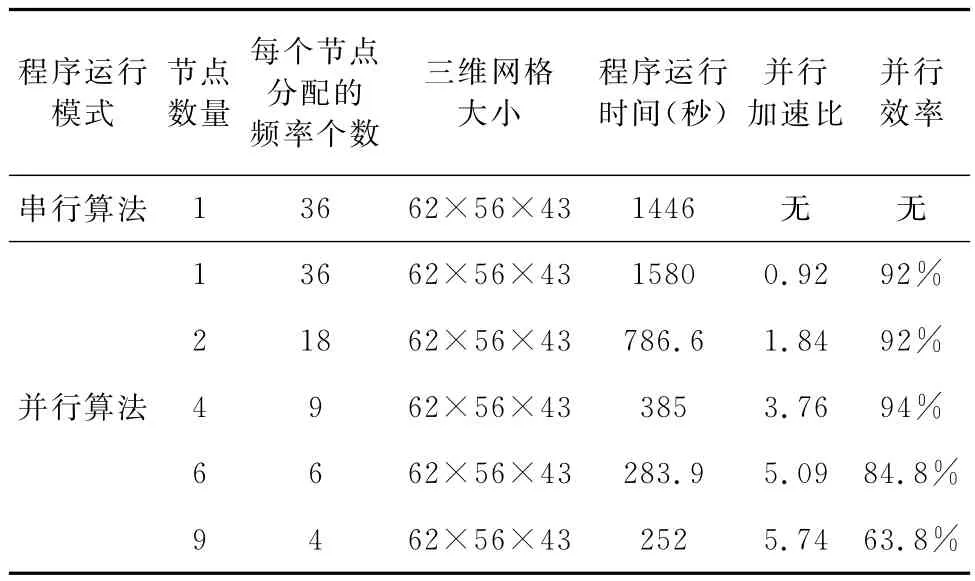
表1 3D／2D模型正演测试时间统计表Table 1 Statistical runtime data for 3D／2Dforward modeling

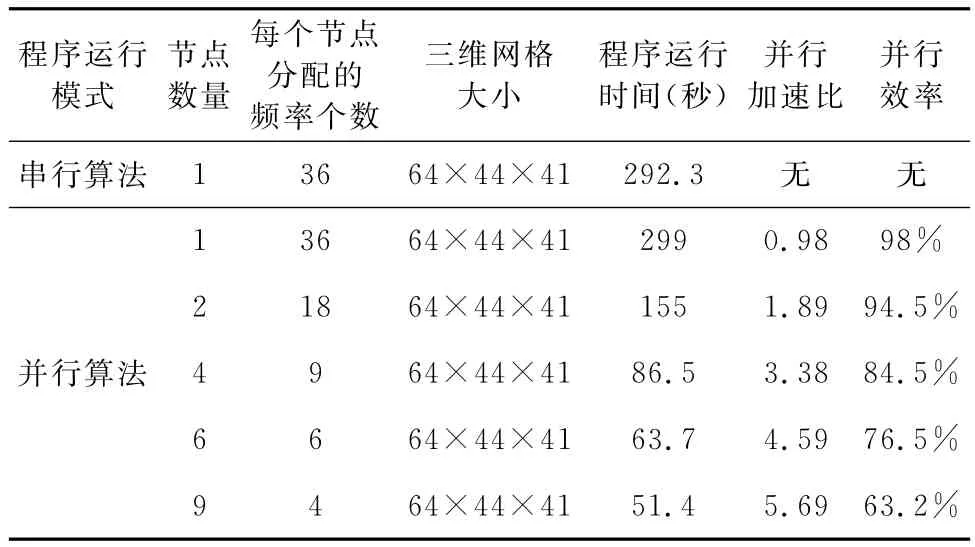
表2 低阻高阻组合模型模型正演测试时间统计表Table 2 Statistical runtime data for combination model of low resistance and high resistance forward modeling

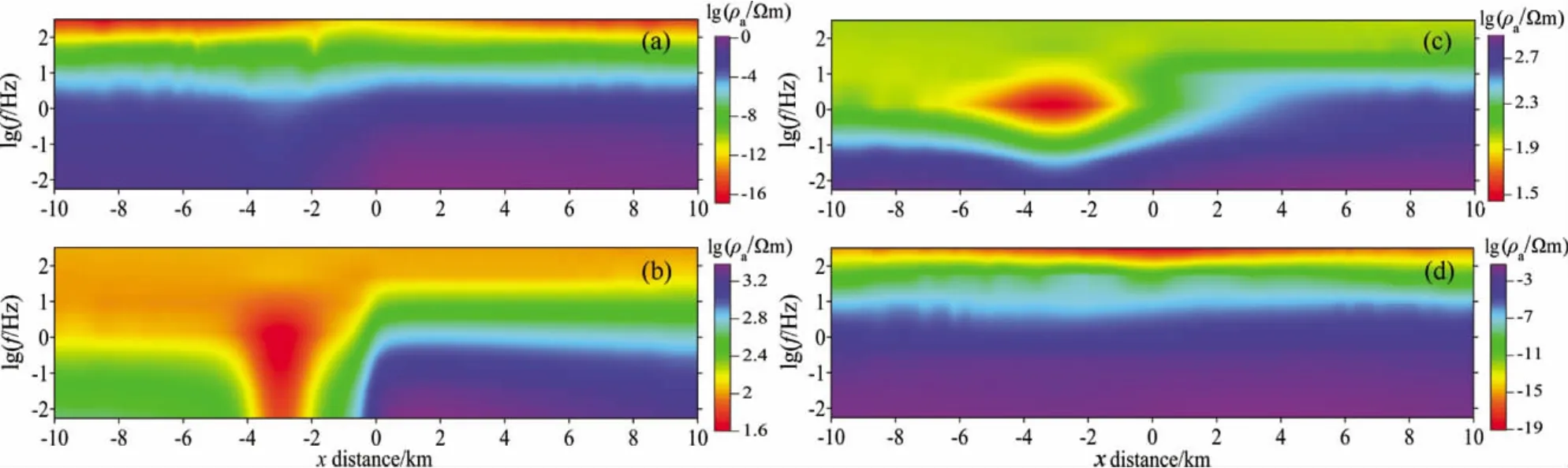
图4 剖面y＝0时视电阻率响应拟断面图（a）ρXX；（b）ρXY；（c）ρYX；（d）ρYY.Fig.4 Pseudo－section of apparent resistivity at y＝0

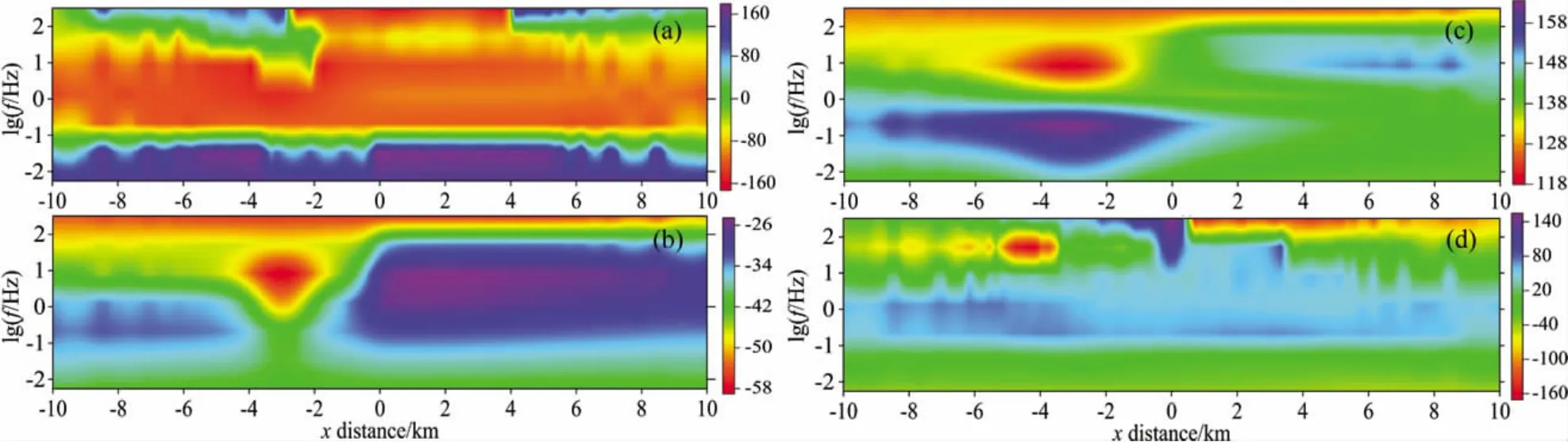
图5 剖面y＝0时相位响应拟断面图（a）φXX；（b）φXY；（c）φYX；（d）φYY.Fig.5 Pseudo－section of tensor phase at y＝0

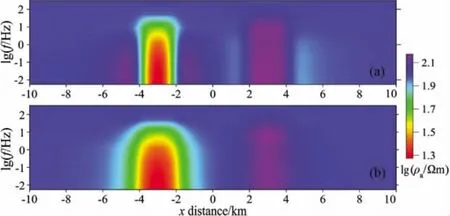
图7 剖面y＝0时视电阻率响应拟断面图（a）ρXY；（b）ρYX.Fig.7 Pseudo－section of apparent resistivity at y＝0

图8 剖面y＝0时相位响应拟断面图（a）φXY；（b）φYX.Fig.8 Pseudo－section of tensor phase at y＝0

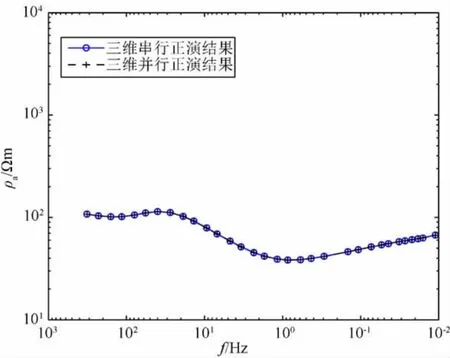
图9 串行正演与并行正演结果对比图Fig.9 The comparison of serial and parallel forward modeling

对表1和表2进行分析，当使用2个节点和4个节点时，并行效率很高.使用6个节点和9个节点时加速比虽然增大了，但增加的幅度不大，并行效率没有2个和4个时高，这是因为随着节点的增加，用于节点间的通信所占的比例逐渐增大，并行效率反而下降.因此如何减少节点间通信量是并行程序开发的关键.另外，一个节点的并行计算时间要比同一节点的串行计算时间要长，这是因为节点内有少量的通信以及一些管理上的开销.从表中总的可以看出并行计算的效果还是很明显的，尤其是当计算量很大时，并行优越性更能体现.

6 结 语

大地电磁三维反演推广应用的最大障碍是计算规模巨大，耗费时间很长，普通微机往往难以承受.而反演中绝大部分计算时间花费在正演或者与正演有关的运算上，因此加快正演计算速度是提高反演计算速度的关键，并行计算为有效解决三维大地电磁计算问题提供了一个最优途径.本文在曙光TC5000A高性能计算平台上，以MPI为并行编程环境，实现了大地电磁三维交错网格有限差分数值模拟并行算法.通过理论模型试算和分析，结果证明了该并行算法的正确性和高效性，很好的解决了三维正演计算速度问题，为进一步的大地电磁三维反演并行算法研究奠定了重要基础.

（References）

［1］胡祥云，胡祖志，张荣等.油气MT勘探COPROD－2S1模型数据的二维反演.天然气工业，2004，25（9）：33－37.Hu X Y，Hu Z Z，Zhang R，et al.Two dimensional inversion of COPROD－2S1modeling dataset in oil and gas magnetotelluric exploration.Natural Gas Industry （in Chinese），2004，25（9）：33－37.

［2］谭捍东，魏文博，Unsworth M等.西藏高原南部雅鲁臧布江缝合带地区地壳电性结构研究.地球物理学报，2004，47（4）：685－690.Tan H D，Wei W B，Unsworth M，et al.Crustal electrical conductivity structure beneath the Yarlung Zangbo Jiang structure in the southern Xizang plateau.Chinese J.Geophys.（in Chinese），2004，47（4）：685－690.

［3］叶益信，胡祥云，金钢燮等.大地电磁二维陡边界反演应用效果分析.地球物理学进展，2009，24（1）：668－674.Ye Y X，Hu X Y，Jing G X，et al.Application analysis of sharp boundary inversion of magnetotelluric data for 2D structure.Progress in Geophys （in Chinese），2009，24（1）：668－674.

［4］胡祖志，胡祥云，何展翔.大地电磁非线性共轭梯度拟三维反演.地球物理学报，2006，49（4）：1226－1234.Hu Z Z，Hu X Y，He Z Z.Pseudo－Three－Dimensional magnetotelluric inversion using nonlinear conjugate gradients.Chinese J.Geophys.（in Chinese），2006，49（4）：1226－1234.

［5］杨迪琨，胡祥云.含噪声数据反演的概率描述.地球物理学报，2008，51（3）：901－907.Yang D K，Hu X Y.Inversion of noisy data by probabilist methodology.Chinese J.Geophys.（in Chinese），2008，51（3）：901－907.

［6］谭捍东，余钦范，Booker J等.大地电磁法三维快速松弛反演.地球物理学报，2003，46（6）：850－854.Tan H D，Yu Q F，Booker J，et al.Three－Dimensional rapid relaxation inversion for the magnetotelluric method.Chinese J.Geophys.（in Chinese），2003，46（6）：850－854.

［7］张林波，迟学斌，莫则尧等.并行计算导论.北京：清华大学出版社，2006.Zhang L B，Chi X B，Mo Z Y，et al.Introduction to Parallel Computing.Beijing：Tsinghua University Press，2006.

［8］都志辉 编著.高性能计算并行编程技术－MPI并行程序设计.北京：清华大学出版社，2001.Du Z H.High－Pwered Computing Parallel Programming Technique－MPI Parallel Program Design （in Chinese）.Beijing：Tsinghua University Press，2001.

［9］Hohmann G W.There－dimensional induced polarization and electromagnetic modeling.Geophysics，1975，40（2）：309－324.

［10］Rodi W L.A technique for improving the accuracy of finite element solutions for magnetotelluric data.Geophys.J.Roy.Astr.Soc.，1976，44（2）：483－506.

［11］Wannamaker P E，Stodt J A，Rijo L.Two－dimensional topographic responses in magnetotelluric modeled using finite elements.Geophysics，1986，51（11）：2131－2144.

［12］Mitsuhata Y，Uchida T.3Dmagnetotelluric modeling using the T－Ωfinite－element method.Geophysics，2004，69（1）：108－119.

［13］Mackie R L，Smith J T，Madden T R.There－dimensional electromagnetic modeling using finite difference equations：The magnetotelluric example.Radio Science，1994，29（4）：923－935.

［14］Smith J T.Conservative modeling of 3－D electromagnetic fields，Part I：Properties and error analysis.Geophysics，1996，61（5）：1308－1318.

［15］Smith J T.Conservative modeling of 3－D electromagnetic fields， Part II： Biconjugate gradient solution and an accelerator.Geophysics，1996，61（5）：1319－1324.

［16］Wannamaker P E， Hohmann G W，SanFilipo W A.Electromagnetic modeling of three－dimensional bodies in layered earths using integral equations.Geophysics，1984，49（1）：60－74.

［17］Wannamaker P E.Advances in three－dimensional magnetotelluric modeling using integral equations.Geophysics，1991，56（11）：1716－1728.

［18］Xiong Z H.Electromagnetic modeling of three－dimension structures by the method of system iteration using integral equations.Geophysics，1992，57（12）：1556－1561.

［19］Siripunvaraporn W，Egbert G.An efficient data－subspace inversion method for 2－D magnetotelluric data.Geophysics，2000，65（3）：791－803.

［20］Siripunvaraporn W， Uyeshima M， Egbert G. Threedimensional inversion for Network－Magnetotelluric data.Earth Planets Space，2004，56（9）：893－902.

［21］Siripunvaraporn W，Egbert G，Lenbury Y，et al.Threedimensional magnetotelluric inversion：data－space method.Physics of the Earth and Planetary Interiors，2005，150（1－3）：3－14.

［22］Siripunvaraporn W，Egbert G. WSINV3DMT： Vertical magnetic field transfer function inversion and parallel implementation.Physics of the Earth and Planetary Interiors，2009，173（3－4）：317－329.

［23］胡祖志，胡祥云.大地电磁三维反演方法综述.地球物理学进展，2005，20（1）：214－220.Hu Z Z， Hu X Y. Review of there dimensional magnetotelluric inversion methods.Progress in Geophys （in Chinese），2005，20（1）：214－220.

［24］Lin C H，Tan H D，Tong T.Three－dimensional conjugate gradient inversion of magnetotelluric full information data.Applied Geophysics，2011，8（1）：1－10.

［25］谭捍东，余钦范，Booker J等.大地电磁法三维交错采样有限差分数值模拟.地球物理学报，2003，46（5）：705－711.Tan H D，Yu Q F，Booker J，et al.Magnetotelluric threedimensional modeling using the staggered－grid finite difference method.Chinese J.Geophys.（in Chinese），2003，46（5）：705－711.