庐枞矿集区大地电磁测深强噪声的影响规律

汤井田，徐志敏，肖 晓，李 晋

1 中南大学地球科学与信息物理学院，长沙 410083

2 西北综合勘察设计研究院，西安 710003

1 引 言

大地电磁测深法（MT）假设来自遥远的天然电磁场以均匀平面电磁波垂直入射到地球表面.天然电磁场频率范围很宽，信号微弱，极化方向随机，因此大地电磁信号极易受到各种噪声干扰［1－2］.影响大地电磁测深资料的噪声可以分为工频干扰、地质噪声和其它外界和观测系统不稳定引起的随机干扰，它们分别来自不同的源［3－5］.其中工频干扰基本上产生于测点周围的人工电磁系统与环境特征，为近场干扰；地质噪声主要包括静位移畸变和地形影响，通常是全频域的；而大功率供电系统的不稳定则主要影响低频.

抑制噪声干扰，最初甘布尔等提出了一种互功率谱法［6－7］，由于自功率谱中包含有噪声的成分，因此低信噪比将会不可避免的降低，采取在计算阻抗时完全使用互功率谱而不用自功率谱的方法就会大大降低噪声的影响，具有一定的抑制噪声干扰的作用；而在对大地电磁资料误差分布规律的分析与研究中许多学者提出，MT资料的误差分布并不完全遵循高斯误差分布［8－11］，所以建立在高斯误差分布之上的最小二乘阻抗张量估算法，将会导致处理结果的分散或偏离.为此，Egbert G D、Booker J R、林长佑等将Robust统计法引入到大地电磁测深法的阻抗张量估算中，提出了大地电磁Robust处理方法；在压制人文干扰对MT数据资料的影响以及抑制局部和区域性电磁噪声上，远参考大地电磁测深法（Remote Reference MT，RRMT），以远参考点与测点之间噪声的不相关性特征为依据，通过阻抗估计进而压制了不相关噪声的干扰［12－15］.近地表电性不均匀体和地形起伏的影响使大地电磁测深数据的卡尼亚电阻率－相位曲线发生畸变，称为静态效应或静位移，国内外大地电磁学者对静态效应的校正进行了广泛的研究［16－18］，其成果可归纳为直接校正法、联合反演法、电磁阵列剖面（EMAP）法和阻抗张量分解技术等.综合以上调研，目前存在的问题是对强的相关噪声还没有有效的压制方法.

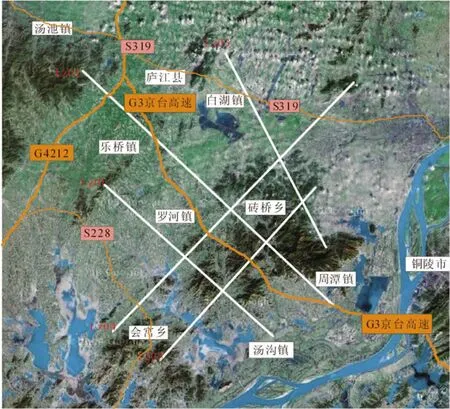
图1 庐枞矿集区MT测线布置Fig.1 MT survey line layout in the ore cluster area of Luzong

庐江—枞阳矿集区位于安徽省境内，经过三县两市辖区，涉及约40个乡镇.测区内人口稠密、水系发育、交通网密布、通信电力网发达，另有较多的矿山正在开采，错综复杂的干扰源，为MT数据的采集和处理带来了许多困难.按深部探测实验研究专项课题（SinoProbe－03）的要求，在区内部署了5条综合地球物理测线（图1）.测线总长约325km，设计MT测点655个，频率范围320Hz～2000s.由于高山地形、水域、城镇、矿山及电力干扰等影响，实际完成MT测点523个.数据采集共投入6套加拿大凤凰公司的V5－2000宽频带大地电磁系统，配备MTC－50磁传感器.数据采集由于高频采样率较高，如果全时间段采集，数据量将会很大，因此高频采集采取抽样采集的办法，采集的起止时间段与低频起止时间段相同，采用1－8－5模式，即每5min采集一次高频或中频的样（高频和中频交替采集），其中有1s的高频数据（采样率2560个样／s），连续8s的中频数据（采样率320个样／s）.低频数据（采样率24个样／s）为全时间段采集.滤波频率设为50Hz.通过测量AC和DC电位差，观察饱和数据的比例，设置合理的增益.通过试验，每个MT测点数据采集时间不低于20个小时.

2 参考点（Y1650）时间序列及测深曲线特征

图2为参考点Y1650时间域波形片段，分析该点电磁场时间域数据，可以发现很多脉冲状波形，且幅值大（比通常的大地电磁信号大1个量级以上），能量较强，但整体时间域数据无其它非平稳信号，符合平稳随机的天然大地电磁场特征.

图3是选自云南某地数据点Y1650的MT卡尼亚电阻率及相位测深曲线，及相干度和信噪比曲线.在等间隔双对数坐标中，Y1650点（图3a）的卡尼亚电阻率曲线全频段基本是连续光滑变化的，误差棒小，符合理论预期.320～0.1Hz频段两种模式轻度分离，应是受到“静态效应”影响；相干度仅低频段最后四个频点较差，其余频段均在0.8以上，320～0.2Hz频段达到了0.9以上；信噪比仅在0.1Hz、0.004Hz、0.0007Hz、0.0005Hz这四个频点处低于0.8，其它频点均在0.9左右，从卡尼亚电阻率及相位测深曲线、相干度和信噪比的分析表明，该点数据质量较好，符合实验要求.

3 强噪声波形特征及其分布规律

对庐枞矿集区523个MT测点的时间域波形进行了详细的分析统计，得到了矿集区典型强噪声的波形特征及其分布规律.

如图4所示，方波噪声在大地电磁测深数据的时间序列中表现为非正弦曲线的波形，呈类方波形态，其幅值很大，通常是正常信号的几个数量级，多出现于24Hz采样率电道数据中，通过对方波噪声的频谱分析，我们发现其影响频带范围为10Hz以后的中低频段.

如图5所示，三角波噪声在大地电磁测深数据的时间序列中表现为非正弦曲线的锯齿波形，呈类三角形态，其幅值很大，多出现于24Hz采样率磁道数据中.通过对三角波噪声的频谱分析，我们发现其影响频带范围在10Hz以后的中低频段，其中0.1～0.01Hz的低频段最为严重.

如图6所示，阶跃噪声在大地电磁测深数据的时间序列中表现为大地电磁信号的突然抬升（或下降）然后向下（或向上）逐渐趋于正常大地电磁信号幅值的波形形态，其幅值可以是正常信号的若干倍甚至几个数量级，阶跃噪声存在于大地电磁测深数据的24Hz、2560Hz采样率的电道Ex、Ey或者磁道Hx、Hy中，相应的磁道或者电道表现为脉冲噪声.通过对阶跃噪声的频谱分析，我们发现阶跃噪声提取于高频2560Hz采样率中时，其频谱能量在10～1Hz频段达到最大值，当阶跃噪声提取于低频24Hz采样率中时，其频谱能量在0.1Hz以后的低频段达到最大值，因此其影响频带范围主要为10～1Hz、0.1Hz以后的低频段.

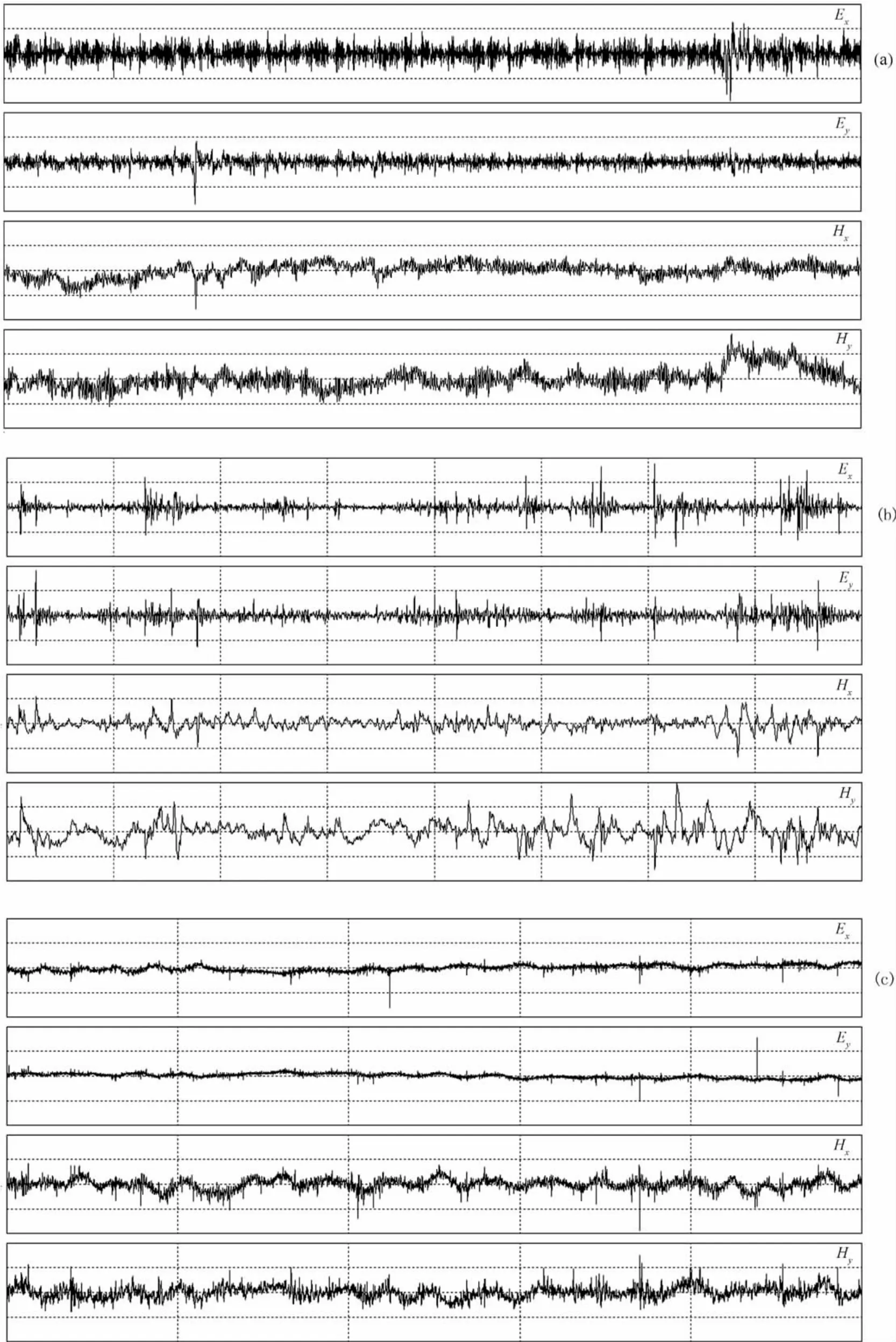
图2 参考点Y1650时间序列曲线（a）2560Hz采样率；（b）320Hz采样率；（c）24Hz采样率.Fig.2 Curve of time series at reference point Y1650（a）2560Hz sampling rate；（b）320Hz sampling rate；（c）24Hz sampling rate.

图3 Y1650卡尼亚电阻率及相位测深曲线（a）、相干度曲线（b）以及信噪比曲线（c）Fig.3 （a）Cagniard resistivity and phase sounding curves，（b）degree of coherence，and（c）SNR at Y1650

如图7所示，脉冲噪声在大地电磁测深数据的时间序列中表现为尖峰形态，其幅值可以是正常信号的若干倍甚至几个数量级，脉冲噪声存在于大地电磁数据的所有采样率中，可见其影响范围之广.通过对脉冲噪声的频谱分析，我们发现脉冲噪声提取于高频2560Hz采样率中时，其频谱能量在100～1Hz频段均匀分布，当脉冲噪声提取于低频320Hz采样率中时，其频谱能量在10～0.1Hz频段均匀分布，当脉冲噪声提取于低频24Hz采样率中时，其频谱能量在1～0.001Hz频段均匀分布，而脉冲噪声一般在大地电磁原始数据中全频段均有出现，因此其影响频带范围为大地电磁数据的全频段.

如图8所示，充放电噪声在大地电磁测深数据的时间序列中表现为充电、放电形态，其幅值也较大，可以是正常信号的若干倍甚至几个数量级，充放电噪声通常存在于大地电磁数据320Hz采样率电道和磁道数据中.通过对充放电噪声的频谱分析，我们发现充放电噪声仅出现于320Hz采样率的原始数据中，其频谱能量在10～0.1Hz频段达到最大值，因此其影响频带范围为10～0.1Hz.

对庐枞强噪声的分析发现，类方波噪声是影响强度最大的一类噪声，一般出现在24Hz采样率的电场信号中，在磁场信号中同时伴随有类三角波噪声.类阶跃波噪声也多出现在电道或者磁道的24Hz采样率信号中，2560Hz采样率信号中出现的多是尖峰干扰.类充放电噪声只存在于320Hz采样率信号中，一般同时出现在电道和磁道中.频谱分析表明，这些明显由人工源电磁场引起的强噪声一般在10～0.1Hz频率范围内，对卡尼亚电阻率和相位的影响严重.

4 强噪声对MT测深曲线的影响规律

为进一步分析这类强噪声对测深曲线的影响规律，我们选择基本没受干扰影响的Y1650点作为参考点，根据前文对庐枞强噪声的归纳结果，应用广义形态滤波对实测时间序列进行噪声分离处理，结果对于大尺度强干扰噪声具有较好的效果［19］.以采样率、幅值和频谱的差异对提取出的噪声进行统计分析，并将其中典型的强干扰时间域波形叠加到Y1650的电磁场时间波形中，然后以合成后的时间域数据进行张量阻抗分析，计算卡尼亚视电阻率、相位、相干度以及信噪比等参数，对比合成前后参考点视电阻率及相位等参数的变化，总结出强噪声的影响规律.

以24Hz采样率为例，图9a是参考点Y1650在14：00—22：00这段时间内任意10min的电场Ex时间域波形，图9b是采用广义形态滤波从电场Ex数据中提取的典型的类方波噪声波形，时长也是10min，将其与图9a波形数据逐点相加，得到加噪后波形如图9c所示.对其它电磁场分量及不同采样率数据采用同样的处理方法，可得到完整的加噪的5个电磁场分量的时间域数据，用V5－2000自带的软件即可进行阻抗分析，计算各种参数.

图4 方波噪声（a）时间序列曲线及其（b）Ex 频谱，（c）Ey 频谱Fig.4 （a）Time series graph and（b）Exspectrogram，（c）Eyspectrogram for square－wave noise

4.1 强噪声对测深曲线的影响规律

图10是对参考点Y1650时间域数据添加不同强噪声后计算的视电阻率和相位曲线.与图10a没有加噪的原始曲线对比，可得出如下规律：

（1）添加类方波、三角波和充放电噪声后，在等间隔双对数坐标下，视电阻率曲线在10～0.01Hz频段呈45°（或大于45°）上升，相位接近或等于0.

（2）类方波、三角波和阶跃噪声对10Hz以下的中低频段影响强烈，但基本不影响10Hz以上频段.

（3）添加类阶跃噪声，1～0.01Hz频段的视电阻率曲线呈45°（或大于45°）上升，相位趋于0；相比于原始曲线，视电阻率曲线在10～1Hz频段下降.

（4）脉冲噪声严重影响全频段阻抗分析的稳定性，使视电阻率－相位曲线在全频段跳变不连续，且在1～0.01Hz频段曲线抬升.

4.2 强噪声对相干度与对信噪比的影响规律

相干度是用来度量两个场之间的相干程度，其定义为：

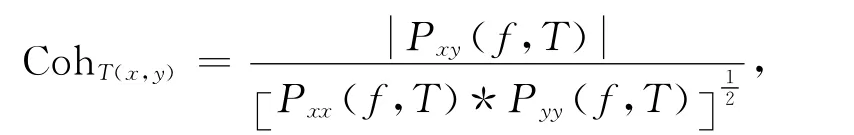
式中f是频率，T是时间序列的长度，Pxx和Pyy是各自的自功率谱，Pxy是它们的互功率谱，相干度可以为0～1之间的实数值.当Coh为0时两个场为不相关的序列，当为1时两个场为线性相关序列.当大地电磁测深数据采集中不包含噪声时，大地电磁场的两对正交分量Ex－Hy和Ey－Hx是线性相关的，即相干度为1，反之当含有的噪声越多，相干度就越差，数值越接近0.

图5 三角波噪声（a）时间序列曲线及其（b）Hx频谱，（c）Hy频谱Fig.5 （a）Time series graph and（b）Hxspectrogram，（c）Hyspectrogram for triangular wave noise

信噪比是研究电、磁场分量资料受到干扰程度的一种方法.因为庐枞大地电磁测深数据采用的是以本地磁场为参考信号计算信噪比，因此磁场的信噪比恒为1，电场的信噪比为单道电场与两道磁场相关系数的平方值（图11中字母FB、SJB、JY、MC和CFD分别为添加方波噪声、三角波噪声、阶跃噪声、脉冲噪声和充放电噪声后数据的简称）.

我们通过研究不同种类型噪声对大地电磁数据相干度的影响规律发现，方波、三角波噪声对大地电磁10Hz以下低频数据相干度影响巨大，且可以分为两个区间，一个是0.1～10Hz频段，该频段内相干度与信噪比均受到了强烈干扰；一个是0.1Hz以下的低频段，该频段由于大地电磁信号微弱，极易受到干扰，而我们所添加的方波噪声强，因此造成该频段相干度与信噪比普遍较低；阶跃噪声对大地电磁10～0.01Hz频段数据影响巨大，0.01Hz以下的低频段由于原始信号信噪比低导致我们添加阶跃噪声后相干度与信噪比均偏低；脉冲噪声对大地电磁全频段数据相干度均有影响，其中0.1Hz附近干扰最为严重；充放电噪声对大地电磁10～1Hz和0.1 Hz以下低频数据相干度影响巨大.本文通过对相干度和信噪比的研究进一步证明了各种强噪声的影响频带范围.

5 结 论

庐枞矿集区内强烈的工业、通讯、矿山、民用等电磁干扰严重污染了大地电磁测深数据，类方波、三角波、充放电波形、尖峰脉冲等强噪声是主要的干扰信号，通常方波、三角波仅存在于24Hz采样率信号中，充放电波形仅存在于320Hz采样率信号中.

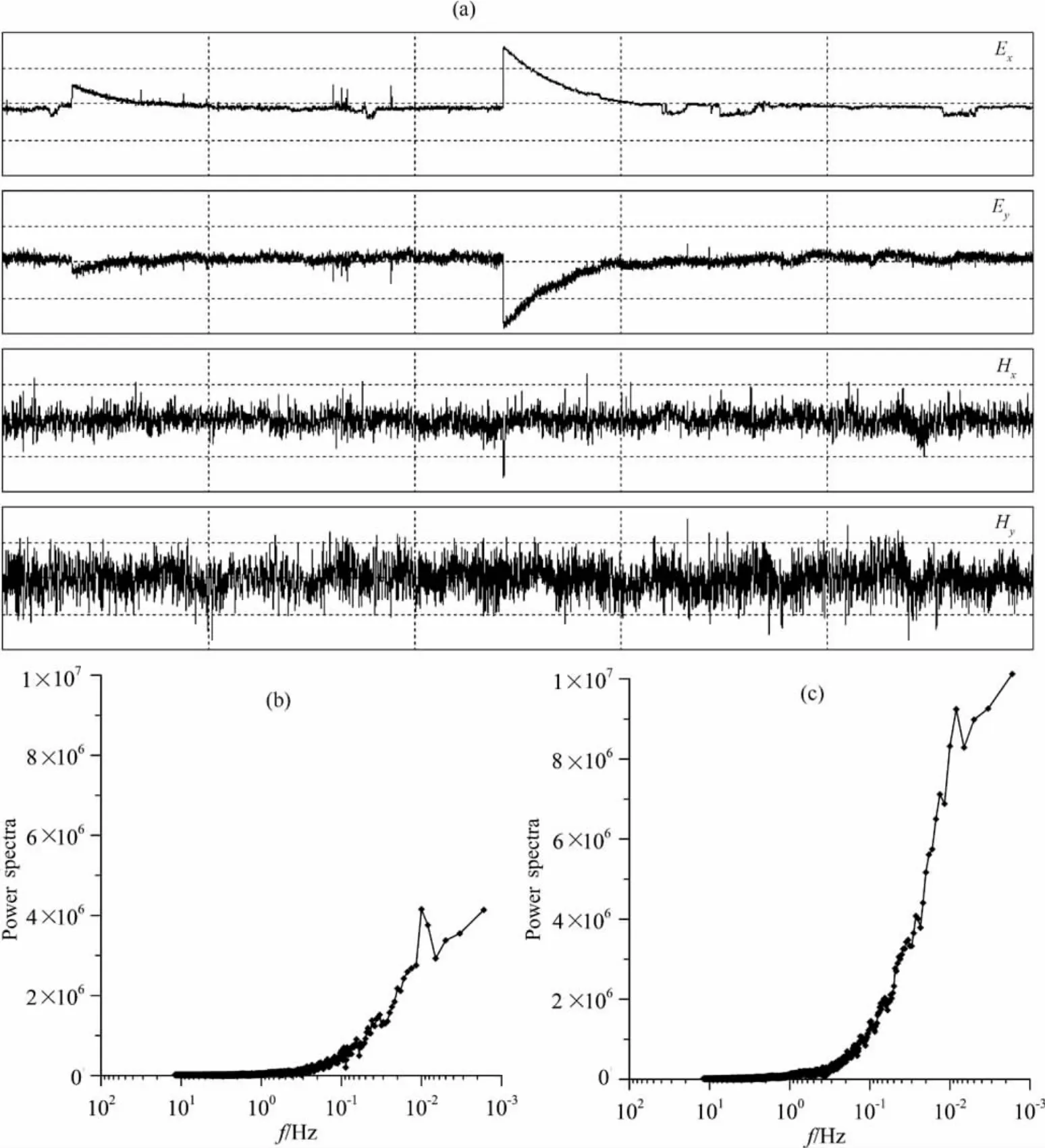
图6 同图5，但为阶跃噪声Fig.6 Same as Fig.5，but for step wave noise

通过将强噪声添加到未受干扰的大地电磁信号中进行仿真，结果表明，类方波、三角波、阶跃波和充放电噪声对大地电磁10Hz以下的中低频段数据影响剧烈，视电阻率曲线呈近似45°抬升，相位趋于零，与可控源音频大地电磁法（CSAMT）近区效应一致.尖峰脉冲噪声使视电阻率曲线在1～0.01Hz频段抬升，且全频段均有不同程度的飞点，曲线形态不明确.这些结论与矿集区实测MT测深曲线的结果是一致的，具有一定的普遍性，也为进一步压制这类强干扰提供了依据.

对此类强干扰噪声可采用广义形态滤波的方法进行压制，汤井田等一文［19］中有较详细论述，为节省篇幅，本文不再讨论.

（References）

［1］考夫曼，凯勒.大地电磁测深法.刘国栋译.北京：地震出版社，1987.Kaufman A A，Keller G V. Magnetotelluric Sounding Method （in Chinese）.Translated by Liu G D.Beijing：Seismological Press，1987.

［2］陈乐寿，王光锷.大地电磁测深法.北京：地质出版社，1990.Chen L S，Wang G E.Magnetotelluric Sounding Method（in Chinese）.Beijing：Geological Publishing House，1990.

［3］徐志敏，汤井田，强建科.矿集区大地电磁强干扰类型分析.物探与化探，2012，36（2）：214－219.Xu Z M，Tang J T，Qiang J K.An analysis of the magnetotelluric strong interference types in ore concentration areas.Geophysical and Geochemical Exploration （in Chinese），2012，36（2）：214－219.

［4］孙洁，普光文，白登海等.大地电磁测深资料的噪声干扰.物探与化探，2000，24（2）：119－127.Sun J，Jin G W，Bai D H，et al.The noise interference of magnetotelluric sounding data.Geophysical and Geochemical Exploration（in Chinese），2000，24（2）：119－127.

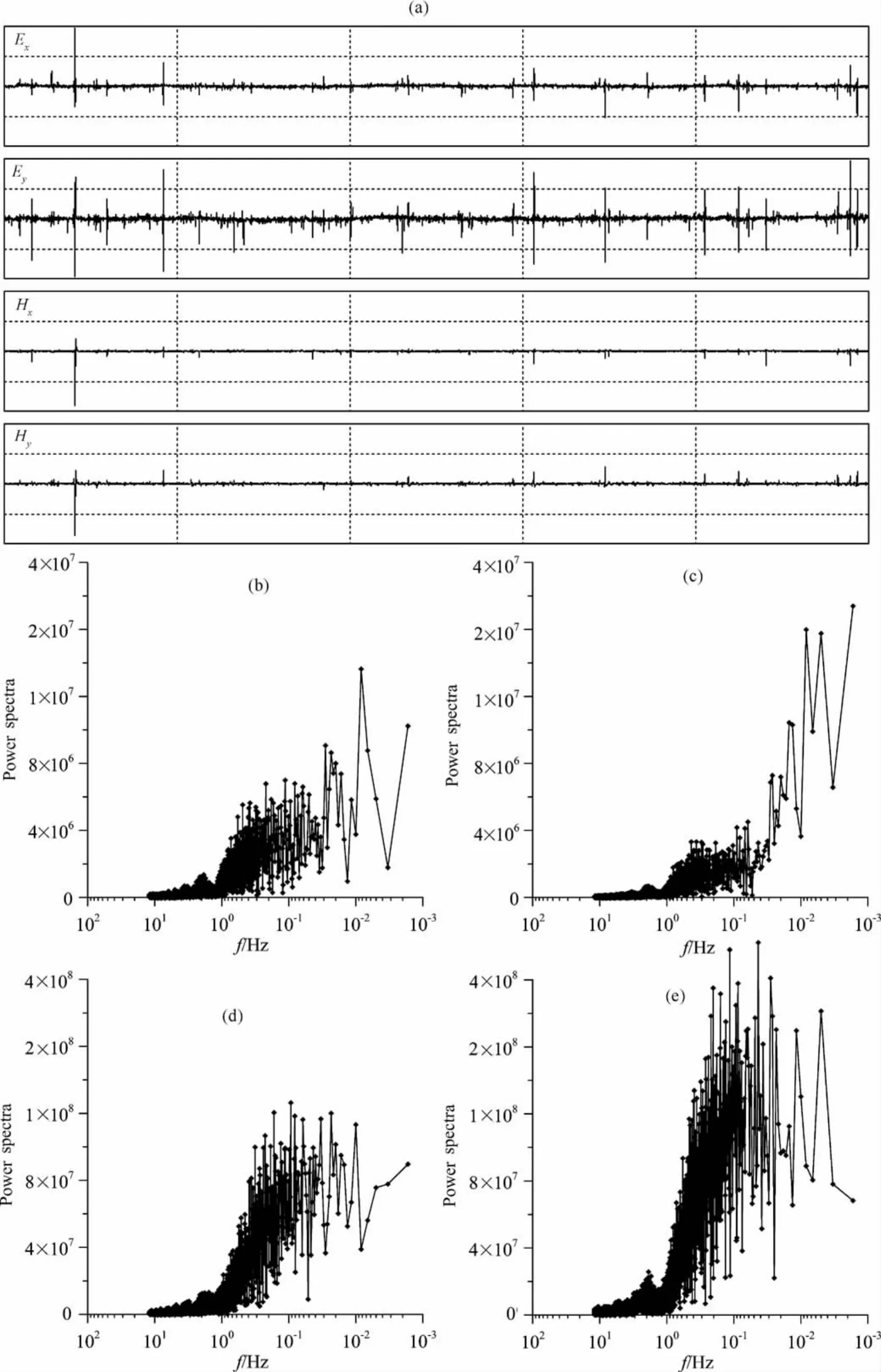
图7 脉冲噪声（a）时间序列曲线及其（b）Ex 频谱，（c）Ey 频谱，（d）Hx 频谱，（e）Hy 频谱Fig.7 （a）Time series graph and（b）Exspectrogram，（c）Eyspectrogram，（d）Hxspectrogram，（e）Hyspectrogram for impulse wave noise

图8 同图7，但为充放电噪声Fig.8 Same as Fig.7，but for charge and discharge wave noise

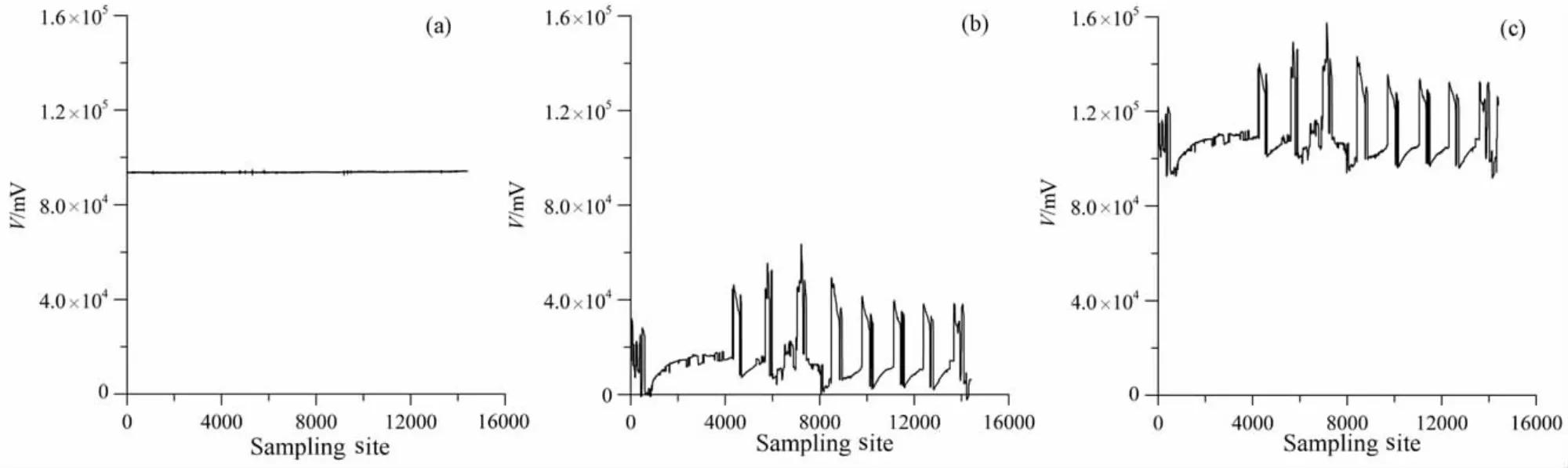
图9 噪声添加过程示意图（a）参考点Y1650原始时间序列曲线；（b）方波噪声电道Ex时间序列曲线；（c）参考点Y1650电道Ex添加方波噪声后时间序列曲线.Fig.9 Schematic diagram of noise adding process（a）Original time series graph at reference point Y1650；（b）Time series graph for square-wave noise power road Ex；（c）Time series graph for power road Exadd the square-wave noise at reference point Y1650.

图10 参考点Y1650添加噪声前后卡尼亚电阻率－相位测深曲线对比（a）加噪前；（b）加入方波噪声后；（c）加入三角波噪声后；（d）加入阶跃噪声后；（e）加入脉冲噪声后；（f）加入充放电噪声后.Fig.10 Comparison of Cagniard resistivity and phase sounding curves at reference point Y1650before and after adding noise（a）Before adding noise；（b）After adding square-wave noise；（c）After adding triangular wave noise；（d）After adding step wave noise；（e）After adding impulse wave noise；（f）After adding charge and discharge wave noise.

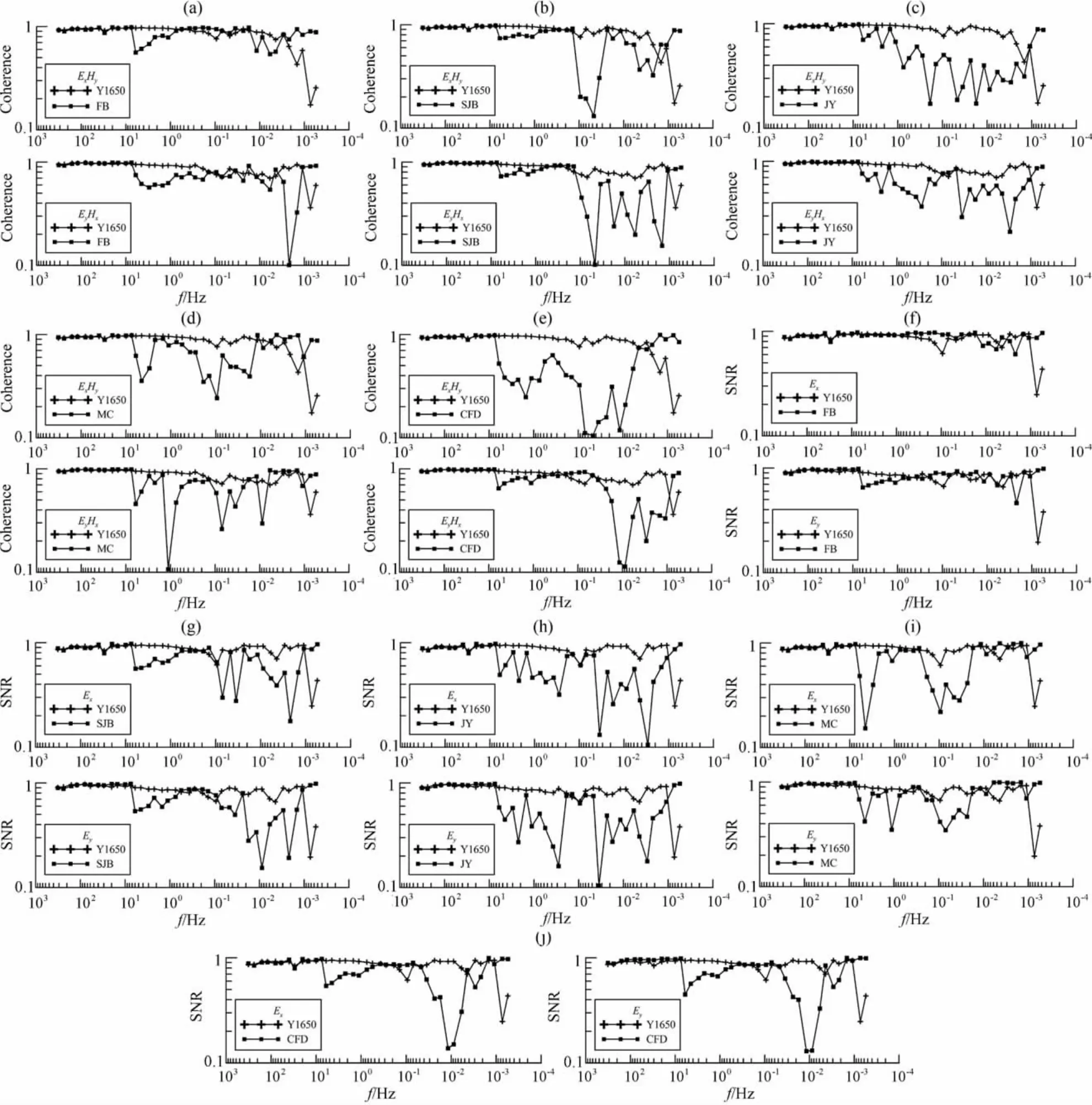
图11 参考点Y1650添加噪声前后相干度（a—e）对比、信噪比（f—j）对比（a，f）加入方波噪声前后；（b，g）加入三角波噪声前后；（c，h）加入阶跃噪声前后；（d，i）加入脉冲噪声前后；（e，j）加入充放电噪声前后.Fig.11 Comparisons of（a—e）coherence degree and（f—j）SNR at reference point Y1650before and after adding noise（a，f）Before and after adding square-wave noise；（b，g）Before and after adding triangle-wave noise；（c，h）Before and after adding step-wave noise；（d，i）Before and after adding impulse noise；（e，j）Before and after adding charge-discharge noise.

［5］胡家华，陈清礼，严良俊等.MT资料的噪声源分析及减小观测噪声的措施.江汉石油学院学报，1999，21（4）：69－71.Hu J H，Chen Q L，Yan L J，et al.Analyzing noise sources of MT data and minimizing measurement noise.Journal of Jianghan Petroleum Institute （in Chinese），1999，21（4）：69－71.

［6］Gamble T D，Goubau W M，Clarke J.Magnetotellurics with a remote magnetic reference.Geophysics，1979，44（1）：53－68.

［7］邓前辉，白改先.互功率法在大地电磁阻抗张量估算中的应用.石油地球物理勘探，1982，（4）：57－64.Deng Q H，Bai G X.Crosspower method applied in the estimation of magnetotelluric impendance tensor.Oil Geophysical Prospecting（in Chinese），1982，（4）：57－64.

［8］杨生.大地电磁测深法环境噪声抑制研究及其应用［博士论文］.长沙：中南大学，2004.Yang S.The study of restraining environmental noise and its application in magnetotelluric sounding ［Ph.D.thesis］（in Chinese）.Changsha：Central South University，2004.

［9］Egbert G D，Booker J R.Robust estimation of geomagnetic transfer functions.Geophys.J.Roy.Astr.Soc.，1986，87（1）：173－194.

［10］Sutarno D，Vozoff K.Robust M－estimation of magnetotelluric impedance tensors.Expl.Geophys.，1989，20（3）：383－398.

［11］林长佑，武玉霞，刘晓玲.大地电磁响应函数的除偏估算和误差的研究.西北地震学报，1988，10（3）：25－38.Lin C Y，Wu Y X，Liu X L.On the unbiased estimation and error research of magnetotelluric response functions.Northwestern Seismological Journal （in Chinese），1988，10（3）：25－38.

［12］严良俊，胡文宝，陈清礼等.远参考MT方法及其在南方强干扰地区的应用.江汉石油学院学报，1998，20（4）：34－38.Yan L J，Hu W B，Chen Q L，et al.Application of remote reference MT to noisy area.Journal of Jianghan Petroleum Institute（in Chinese），1998，20（4）：34－38.

［13］陈清礼，胡文宝，苏朱刘等.长距离远参考大地电磁测深实验研究.石油地球物理勘探，2002，37（2）：145－148.Chen Q L，Hu W B，Su Z L，et al.Study for long－distant and far－referential MT.Oil Geophysical Prospecting （in Chinese），2002，37（2）：145－148.

［14］Ritter O，Junge A，Dawes G.New equipment and processing for magnetotelluric remote reference observations.Geophys.J.Int.，1998，132（2）：535－548.

［15］杨生，鲍光淑，张全胜.远参考大地电磁测深法应用研究.物探与化探，2002，26（1）：27－31，49.Yang S，Bao G S，Zhang Q S.A study on the application of remote reference magnetotelluric sounding technique.Geophysical and Geochemical Exploration （in Chinese），2002，26（1）：27－31，49.

［16］王家映.电磁阵列剖面法的基本原理.地球科学，1990，15（增刊）：1－11.Wang J Y.The basic principle of the electromagnetic array profiling.Earth Science （in Chinese），1990，15（Suppl.）：1－11.

［17］Bahr K.Interpretation of the magnetotelluric impedance tensor：regional induction and local telluric distortion.J.Geophys.，1989，62：119－129.

［18］杨生，鲍光淑，李爱勇.MT法中静态效应及阻抗张量静态校正法.中南工业大学学报（自然科学版），2002，33（1）：8－13.Yang S，Bao G S，Li A Y.The static migration to MT data and the impedance tensor static correction method.Journal of Central South University of Technology （Natural Science）（in Chinese），2002，33（1）：8－13.

［19］汤井田，李晋，肖晓等.数学形态滤波与大地电磁噪声压制.地球物理学报，2012，55（5）：1784－1793.Tang J T，Li J，Xiao X，et al.Mathematical morphology filtering and noise suppression of magnetotelluric sounding data.Chinese J.Geophys.（in Chinese），2012，55（5）：1784－1793.