并行矢量有限元法分析新型波导侧面馈电天线

彭文峰 宛 汀 郭继承

（南京理工大学通信工程系，江苏 南京210094）

引 言

天线在现代通信领域中具有广阔的应用前景，因此，天线的分析与设计引起了越来越多的关注。在天线的电磁特性分析中，谱域方法、矩量法和有限差分法均是常用的数值分析方法［1］。有限元法在分析这类问题时，具有其独特的优越性。首先，有限元法能够精确拟合各种具有复杂几何边界的模型；其次，有限元法针对不同媒质具有很强的通用性，因此，特别适合分析结构复杂的模型；此外，有限元法生成稀疏的系数矩阵，求解方便。有限元法是一种基于变分原理和剖分插值的数值分析方法，它首先采用适当的边界条件截断无限大的分析区域，然后将所获得的有限区域离散成一系列小的网格，从而将无限个自由度的原边值问题转化成为有限个自由度的问题，最后再通过有效计算逼近精确值［2］。1969年P.P.Silvester首先将有限元法应用于电磁学领域，随即引起了广泛重视并获得极大发展。传统的节点有限元方法存在伪解且不能处理边缘奇异性，因此在其基础上发展出了矢量有限元方法［3－4］。矢量有限元方法将自由度赋予单元棱边而不是节点，因此又称棱边有限元方法，它克服了节点有限元方法的缺点，将电磁场的有限元分析带入了一个新的时代。

尽管矢量有限元方法大大提高了有限元电磁仿真的能力，但是随着工程应用要求的提高，待求问题的规模越来越大，这给现有计算平台的硬件资源带来了巨大挑战，普通的单台个人计算机（PC机）都面临着内存不足这一问题。采用多台计算机并联的并行平台来扩充计算机的内存并提高计算效率，是解决这一问题的有效方法［5－7］。区域分解法把原始结构分割成一系列小的子结构来单独求解，具有极高的可并行性，从而缩减了计算规模，降低了内存需求。19世纪70年代德国数学家H.A.Schwarz最早提出了区域分解法，用来论证两个互相重叠的和集上拉普拉斯（Laplace）方程的狄利克雷（Dirichlet）问题的解的存在性［8］。在微分类方法领域，经典的重叠型区域分解方法一般基于交替型施瓦茨（Schwarz）方法［9－10］，其计算效率很大程度上依赖于全局迭代收敛速度，且并行度不高，更加行之有效的方法是采用非重叠型区域分解法［11－15］。近年来，在众多非重叠型区域分解法中，一种拉格朗日乘子型的非重叠型区域分解法引起了广泛重视。该方法首先将原始区域分割成一系列非重叠的子区域；然后在各子区域的交界面上引入对偶未知量，即拉格朗日乘子；再通过消去各子区域内部未知量获得关于拉格朗日乘子的线性方程组，并对其进行迭代求解；最后根据求得的交界面上的已知信息来求出各子区域内部的未知量，从而得到整个区域的解［16－18］。

采用一种基于矢量有限元方法的拉格朗日乘子型非重叠型区域分解法来分析一种新型波导侧面馈电天线的电磁特性。采用四面体棱边单元精确拟合复杂的天线模型边界；采用基于拉格朗日乘子的区域分解法将原始三维问题的求解缩减为关于子区域交界面的二维问题，并采用Krylov子空间迭代法对其进行求解；引入Dirichlet型预条件算子和全局粗问题，加速迭代求解的收敛；引入基于分布式存储的并行算法提高计算效率，缓解内存需求。文中针对新型波导侧面馈电天线的数值分析结果充分证明了该方法的正确性和有效性。

1 问题描述及模型建立

图1所示为本文所分析的新型波导侧面馈电天线的模型示意图。该16单元阵列天线由E面T功率合成网络、辐射圆波导、矩形谐振腔、圆波导传输层、印刷式圆极化器组成。信号经功分网络由辐射圆波导激励矩形谐振腔，在每个矩形谐振腔的上面等间距地开有4个长度为14mm、宽度为1.9mm、间距为23mm的辐射缝隙，缝隙辐射的线极化电磁波经直径为16.2mm，高度为4.4mm的圆波导传输后经印刷式圆极化器形成圆极化信号辐射出去。整个阵列天线的尺寸为（长×宽×高）90mm×90 mm×32mm.图1中除16个金属贴片外，其余部分均为有限元法分析所需离散的自由空间。需要指出的是，该波导侧面馈电天线的实际模型中，图1所示部分均为金属衬底上所开的槽。在图1中的馈电端施加波导馈，其形式为TE10模的电场，工作频率为11.95GHz.电磁波在波导中传播，进而在16个金属贴片上激发出电流，向自由空间辐射。采用有限元法进行电磁特性的数值分析第一步是建立有限元分析区域的模型并进行网格离散。分析该波导侧面馈电天线的电磁辐射问题时，由于辐射空间为无限大，需要强加合适的边界条件来截断无限大的分析区域为有限大。完全匹配层（PML）是近年出现的一种极具吸引力的局部边界条件，它不改变有限元矩阵的特性且可以设置得离目标体很近［19］。本文采用PML来作为截断边界，PML的厚取为四分之一自由空间波长。

在完成建立有限元分析所需模型的步骤之后，第二步需要完成的工作是区域的划分，将原始的有限元分析区域划分为多个规模较小的子区域，这是为区域分解法的施加作准备。如图2所示，给出采用两个切割面将原始区域划分成四个子域的情况。完成模型建立和区域划分的操作后即可进行网格离散，本文采用四面体棱边单元来离散整个区域，能够获得很好的边界拟合效果。离散的操作采用ANSYS软件完成，网格尺寸选为十五分之一自由空间波长。考虑到该波导侧面馈电天线模型的复杂性，对其中精细结构部分需要采用更精细网格进行离散以精确拟合真实结构。最后，从ANSYS软件中导出网格离散信息文件，为后面进行有限元区域分解法的计算做好准备。

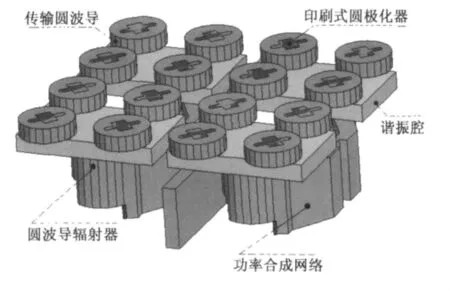
图1 新型波导侧面馈电天线的有限元分析模型示意图

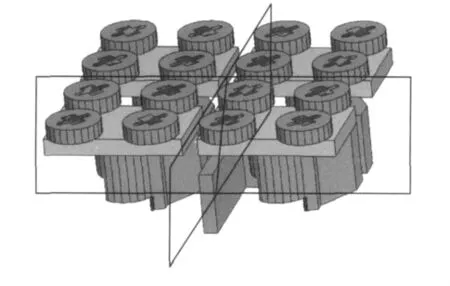
图2 区域划分示意图

2 矢量有限元区域分解法

采用矢量有限元区域分解法分析该波导侧面馈电天线问题的步骤如下：

1）在子区域交界面上引入拉格朗日乘子以及电磁场连续性条件。

2）在每个子区域内建立有限元线性系统，联立获得整个区域的有限元线性系统。

3）采用高斯消去法消去各个子区域的内部未知量，获得仅关于交界面上拉格朗日乘子的线性系统。

4）采用克雷洛夫（Krylov）子空间迭代法求解该线性系统，并引入Dirichlet型预条件算子和全局粗问题，加速迭代求解的收敛。

5）将求出的拉格朗日乘子作为已知边界条件即可求得每个子区域内部各处的场值。

6）根据近场计算远场可获得该天线的辐射特性。需要指出的是，上述所有步骤均具有极高的可并行性，易于在并行平台上实现。下面详细描述有限元区域分解法的基本原理和具体实施。

在本文提出的有限元区域分解法中，原始求解区域Ω被分割成一系列非重叠的子区域Ω1，Ω2，…，Ωn，其中上标1，2，…，n表示各子区域的编号，如图3所示。

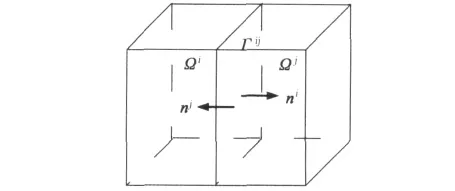
图3 区域划分示意图

图3中，Γij表示子区域i和j的交界面。ni和nj分别表示交界面上指向子域Ωi和Ωj外部的单位法向量。在相邻的子区域交界面上需要满足电场和磁场连续的条件。

根据电场连续性条件，有

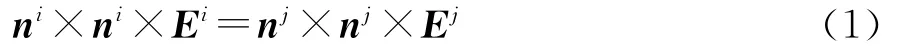
根据磁场连续性条件，有

式（1）和（2）分别是Dirichlet型和诺伊曼（Neumann）型边界条件。从式（2）可以看出，在子域交界面Γij上，定义了一个未知量Λ来表示Neumann型边界条件，Λ又被称为拉格朗日乘子，表示关于交界面未知量的约束条件，从而将子区域的有限元问题转化为一定约束条件下的变分问题。求出未知量Λ后，就可以将其作为已知边界条件来独立地求得各个子区域内部的解。

下面在每个子区域内建立有限元线性系统。子域边值问题描述为

式中：k0为自由空间波数；μr和εr分别表示介质区域的相对介电常数和相对磁导率。需要说明的是，这里采用波导馈电的方式，因此使用的是无源矢量波动方程，馈源以TE10模电场形式施加在馈电端口的棱边上。结合式（2），由变分原理有

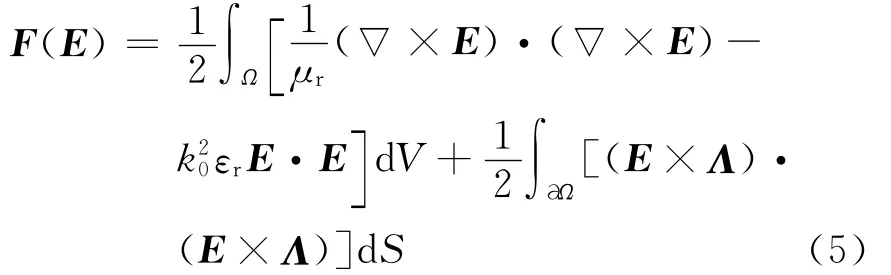
采用矢量棱边基函数展开电场，并令δF（E）＝0，可得第i个子区域的有限元线性系统：

式中：

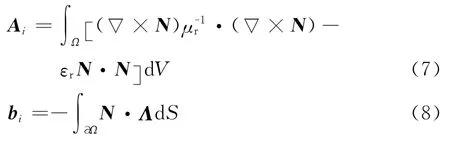
在每个子区域，将待求的未知电场系数分为三种类型

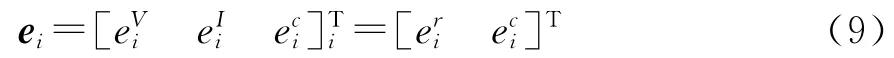
式中，上标V、I和c分别表示子区域内部、相邻子区域交界面和拐角（三个及三个以上子区域交界）处的棱边，把V和I归为一类，记作r，拐角棱边c作为一类。子域矩阵方程可以写作

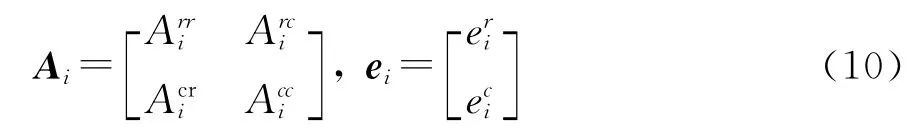
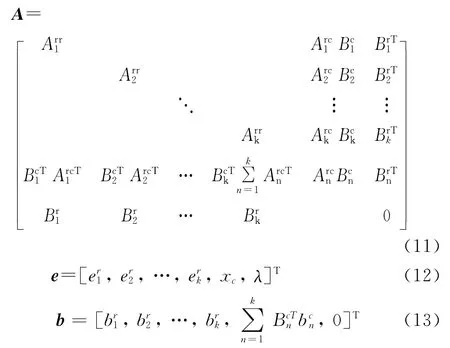
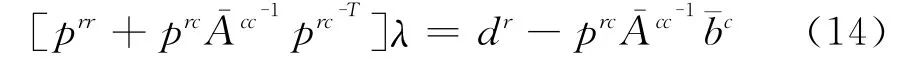
式中各项具体形式如下：

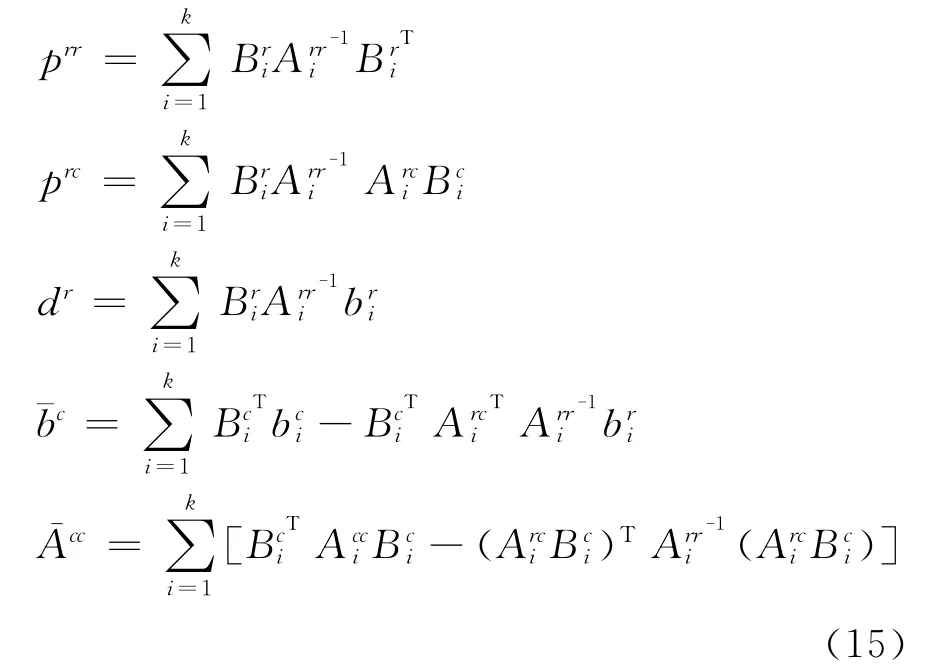
方程组（14）是一个非正定的线性系统，且系数矩阵形式复杂，难以进行直接求解，采用Krylov子空间迭代法中的广义最小余量法（GMRES）来求解。式（15）中，对求逆为主要操作。由于各子区域未知量数目较小，可采用LU分解保存上下三角因子，且各子区域的只分解一次，在Krylov子空间迭代法的每次迭代中只需进行前后向回代即可。此外，映射矩阵和均不参与计算机浮点运算，迭代求解的执行速度非常快。在获得方程组（14）的解之后，通过式（6）即可求出各子区域内的场值。可见，通过引入拉格朗日乘子λ，原始的大型三维问题被缩减为关于交界面的小型二维问题，大大降低了计算复杂度。通常被称作粗问题（Coarse problem）［18］，会在 GMRES的每一次迭代中出现，通过形成全局余量误差来将各个子域联合起来，从而提高了方程组（14）的迭代收敛速度。尽管如此，当矩阵性态较差时，采用普通GMRES方法求解仍会遇到迭代收敛速度慢甚至不收敛的情况，这里引入Dirichlet型预条件算子来改善这一问题，它通过近似式（15）中Prr矩阵的逆来获得良好的迭代加速效果，的具体表达式为

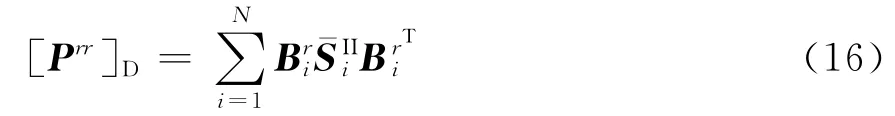
在求得了近场区的电场值之后，天线的辐射方向图可以通过互易定理计算出远区场而得到

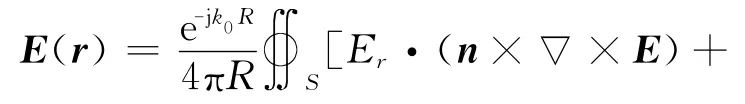
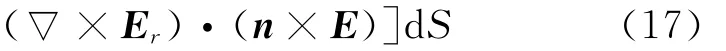
上述步骤中，除了规模很小的Ācc的求逆操作需要在单台计算机上完成之外，其余操作（包括最主要的矩阵的LU分解的操作）均可分配到多台计算机上独立地并行执行，大大提高了计算效率和缓解了内存需求。

3 数值测试

通过对该新型波导侧面馈电天线的数值仿真测试来说明并行有限元区域分解法的正确性和有效性。测试内容为两个方面：第一，验证并行有限元区域分解法计算天线电磁辐射特性的正确性；第二，测试并行有限元区域分解法的并行性能。测试平台为惠普BL680CG5大型刀片式服务器。并行软件环境采用当前流行的基于并行分布式消息传递模型（MPI）的 MPICH2.0软件包。

首先验证本文并行矢量有限元区域分解法的正确性。将整个模型划分为16个子区域，网格离散后总未知量数目为1 608 739，分配给16个进程并行执行该程序。天线的辐射方向图是衡量天线性能的重要图形，首先，采用本文方法计算其辐射方向图，将计算结果和HFSS12.0商用软件包仿真的辐射方向图结构进行对比，如图4和图5所示，分别是主极化和交叉极化的辐射方向图，可以看出，两者吻合得较好。

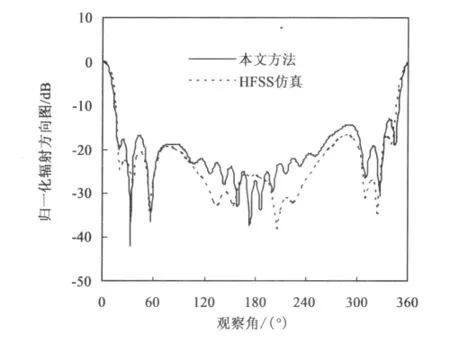
图4 主极化辐射方向图

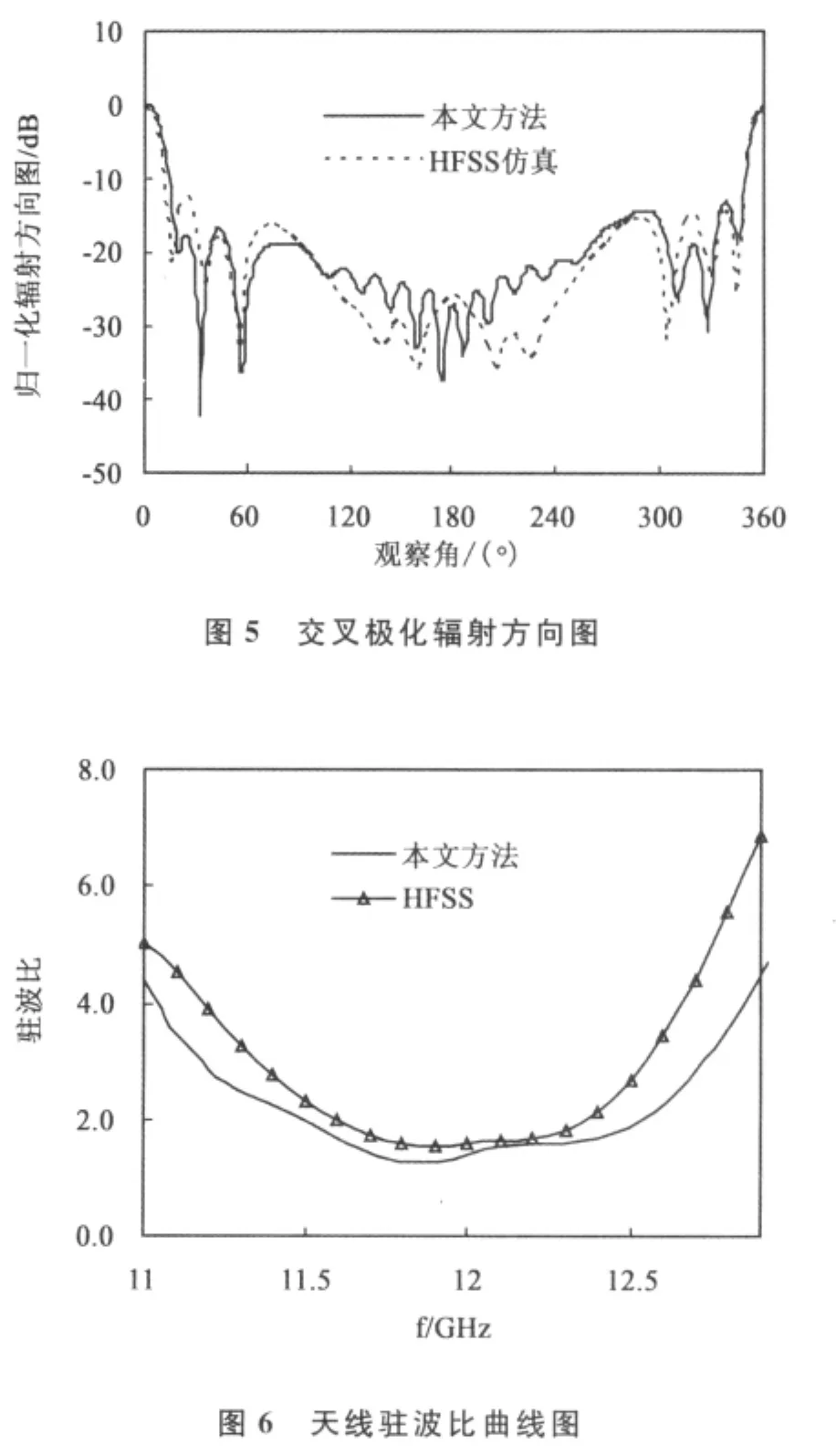
如图6所示，给出了本文方法计算出的驻波比和HFSS12.0仿真结果的比较。可以看出，结果比较吻合。

本文矢量有限元区域分解法固有的并行性使得该算法极易在并行平台上实现。采用并行算法不仅能大大提高问题的求解效率，还能很好地缓解内存需求。并行计算一般有两个重要的衡量指标，一个是并行计算的加速比，另外是一个并行算法的效率。下面测试本文方法的并行性能。并行计算的加速比Sp定义为

并行算法效率是指并行计算的加速比与调用的进程数目的比值，在并行计算中虽然调用多个计算节点共同完成某一项计算任务，但由于各个计算节点之间的通信时间、算法中有的计算任务必须各个进程都需要执行，因此不可能调用多少个处理器就加速多少倍，因此在设计并行程序时应尽量减少通信时间，提高计算的效率。并行效率Ep定义为

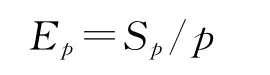
下面测试本文方法的并行计算性能。整个求解共分为16个进程，将这些进程平均分配到1核、4核、8核和16核上测试其并行加速比及并行效率（%），测试结果如表1所示。

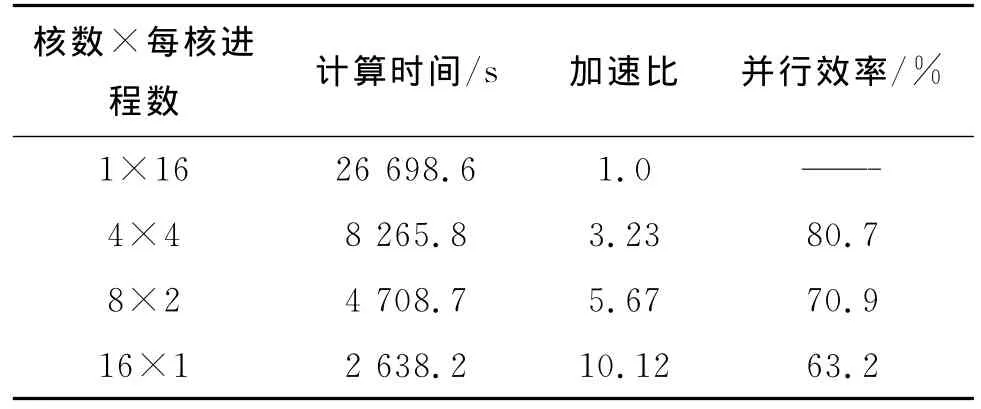
表1 有限元区域分解法并行性能测试

从表1中给出的计算时间可以看出，多个CPU核心的并行处理大大减少了计算时间，同时也缓解了内存的需求。值得注意的是，并行效率随着分配的核数的增加会有所降低，因此在实际操作中，并非分配的核数越多越好，而是要选择合适的核数以获得资源消耗和计算效率的平衡。

4 结 论

采用并行矢量有限元区域分解法成功地对一种新型波导侧面馈电天线进行了分析。该方法采用矢量棱边元精确模拟各处电场；采用区域分解法将原始求解区域分割为一系列小的子区域来求解；在相邻子区域交界面上引入拉格朗日乘子，将原始三维问题缩减为仅关于交界面的二维问题；引入Dirichlet型预条件算子和全局粗问题加速关于拉格朗日乘子系统的迭代收敛；采用基于分布式存储的并行技术大大提高了求解效率并缓解了内存需求。通过给出对新型波导侧面馈电天线数值仿真结果和并行性能的测试，充分证明了这种方法的正确性和有效性。

［1］盛新庆.计算电磁学要论［M］.北京：科学出版社，2004.

［2］JIN J M.The Finite Element Method in Electromagnetics［C］.2nd ed.New York：John Wiley ＆ Sons Inc，2002.

［3］LEE J F.Tangential vector finite elements for electromagnetic field computation［J］.IEEE Transactions on Magnetics，1991，27（5）：4032－4035.

［4］WU J Y，LEE R.The advantages of triangular and tetrahedral edge elements for electromagnetic modelling with the finite element method［J］.IEEE Trans Microwave Theory Tech，1997，45（9）：1431－1437.

［5］崔志伟，韩一平.电大尺寸开口腔体电磁散射的子结构法研究［J］.电波科学学报，2009，24（5）：34－36.CUI Zhiwei，HAN Yipin.The substructure method for scattering by large open－ended cavities［J］.Chinese Journal of Radio Science，2009，24（5）：34－36.（in Chinese）

［6］都志辉，李三立.高性能计算并行编程技术－MPI并行程序设计［M］.北京：清华大学出版社，2001.

［7］Message Passing Interface Forum.MPI：A messagepassing interface standard［J］.Journal of Supercomputer Applications，1994，3（4）：169－414.

［8］SCHWARZ H A.Gesammelete Mathenraticsche Abhandlungen［C］.Berlin：Springer，1890.

［9］BURKHOLDER R J.Forward－backward Interative physical optics algorithm for computing the RCS of open－ended cavities［J］. IEEE Trans Antenna Propag，2005，53（2）：793－799.

［10］OZGUN O，KUZUOGLU M.Forward backward domain decomposition method for finite element solution of electromagnetic boundary value problems［J］.Microwave and Optical Technology Letters，2007，10（49）：2582－2590.

［11］LV Z Q，AN X，HONG W.A fast domain decomposition method for solving three－dimensional largescale electromagnetic problems［J］.IEEE Trans Antennas and Propagation，2008，56（8）：2200－2210.

［12］王小伟，郭 力，葛 蔚，等.高性能并行集群计算环境的构建与性能测试［J］.电波科学学报，2004，25（3）：325－328.WANGXiaowei，GUO Li，GE Wei，et al.Construction of high performance computer cluster and its performance evaluation［J］.Chinese Journal of Radio Science，2004，25（3）：325－328.（in Chinese）

［13］BARKA A，ROUX F.High performance finite elements for the electromagnetic characterization of metamaterials and antenna arrays［C］//Computational Electromagnetics International Workshop （CEM）.Izmir，August 10－13，2011：105－108.

［14］SHAO Y，PENG Z，LEE J F.Signal integrity analysis of high－speed interconnects by using nonconformal domain decomposition method［J］.IEEE Trans Components，Packaging and Manufacturing Technology，2012，2（1）：122－130.

［15］PENG Z，LEE J F.Non－conformal domain decomposition method with mixed true second order transmission condition for solving large finite antenna arrays［J］.IEEE Trans Antennas Propag，2011，59（5）：1638－1651.

［16］LI Y，JIN J M.A vector dual－primal finite element tearing and interconnecting method for solving 3－D large－scale electromagnetic problems［J］.IEEE Trans Antennas Propag，2006，54（10）：3000－3009.

［17］PARASCHOS G N，VOUVAKIS M N.On the Accuracy ofλ－based FETI method for electromagnetic problems［C］//IEEE Antennas and Propagation Society International Symposium （APSURSI）.Toronto，11－17July，2010：1－4.

［18］FARHAT C，AVERY P，TEZAUR R，et al.FETIDPH：A dual－primal domain decomposition method for acoustic scattering［J］.Compute Acoust，2005，13（3）：499－524.

［19］SACKS Z S，KINGSLAND D M，LEE R，et al.Performance of an anisotropic artificial absorber for truncating finite element meshes［J］.IEEE Trans Antennas and Propagation，1995，44（7）：975－982.