三维高斯波束跟踪传播损耗预测改进模型

徐大专 任佳敏 朱秋明 唐亚平 周 剑

（南京航空航天大学电子信息工程学院，江苏 南京210016）

引 言

电波传播特性研究对无线网络规划、设计和优化具有十分重要的意义，已成为当前移动通信技术领域的热点研究课题之一。电波传播预测方法通常可分为确定性方法和实测统计法。实测统计法［1－2］获得的结果直接来源于实测数据，但该方法得到的电磁波传播模型对环境依赖性较大，精度不高，且对测试设备要求较高，使得该方法的实际应用具有一定局限性。确定性分析方法基于电磁波传播理论建立预测模型，预测结果更具有普遍性。目前，已涌现许多类型的确定性分析方法，其中射线跟踪方法因具有预测精度高等优点而获得广泛重视［3－6］。然而，传统射线跟踪法需要跟踪大量绕射射线，还要进行接收球判断，实现比较复杂。本文提出了一种基于三维高斯波束跟踪的电波传播预测改进算法，该方法无需进行接收球判断，通过对射线统一处理可简化预测复杂度，并能够达到较高的精度。文中还提出了一种二维网格加速算法，可大大减小高斯波束与障碍物碰撞检测时间，从而进一步降低该预测算法的运算量。

1 三维高斯波束跟踪模型

假设xoy平面有一x方向极化的平面波，则根据Gabor变换，源场Ex（x，y，0）可分解为一系列高斯窗函数加权之和［7－10］，即

式中：（m，n，p，q）∈Z4，m，n，p，q为移位系数；wmnpq（x，y）表示基准高斯窗函数；lx，ly和kx，ky分别为高斯窗在空域和频域的移位长度。

高斯窗w可表示为

式中Lx，Ly表示高斯窗在x，y方向上的宽度。

假设高斯窗发射的高斯波束为Bmnpq，该波束沿轴线方向 d＝（nkx，qky，）传播，满足＝表示自由空间波数），任意位置高斯波束场可表示为

式中：B0，ξi，μnq分别定义为

μnq为场矢量，Q（zi）表示2×2的曲率复数矩阵，满足以下条件

式中，Id为单位阵。可以证明该矩阵元素可表示为如下形式

式中：Rx（zi）和Ry（zi）为波束的曲率半径；ωx（zi）和ωy（zi）为波束半径，即波束投影到xoy平面时波束横向展开宽度的一半。图1仿真给出了单个高斯波束在空间传播时的场强衰减情况，由图可见高斯波束场强沿轴线方向和横向展宽方向衰减。

任意高斯波束在接收点M处场强可表示为

传统射线跟踪法只在轴线上具有场强，而由式（12）可见高斯波束具有横向展宽宽度，即轴旁一定范围内也有场强，所以只需要考虑反射和透射，无须考虑障碍物边界阴影区的绕射效应。

2 二维网格加速算法

在计算各子波束与墙面作用点时，如果不采用加速算法，需对轴线和场景中每一个墙面进行相交测试获得最近交点，运算量非常大。本文基于计算机视觉领域的二维网格思想［11］，提出一种适用三维高斯波束跟踪的加速算法。该算法伪代码如表1所示，首先将场景划分为若干网格，根据发射点所在坐标定位网格；然后将轴线与该网格内墙面进行相交测试，如不存在交点则进入相邻网格，在下一个网格重复以上操作。

表1 二维网格加0速算法实现

2.1 网格划分及定位

假设场景分成N×M的网格，如图2所示，每个网格大小为n×m.轴线源点坐标为S（x，y，z），可证明S 所在网格号为

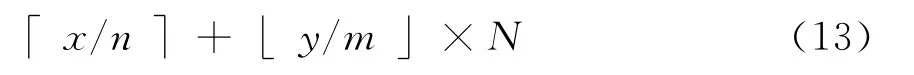
当轴线与网格的交点在网格右边界，且本网格内没有找到交点时，进入右边网格进行相交测试。如果轴线超出场景边界，则可认为轴线与场景中的墙面没有相交点。

图2 网格划分和定位过程

实际场景中网格分割的大小，需要综合考虑每个网格中包含的墙面数目以及网格个数。当网格划分越大，每个网格中包含的墙面数目越多，在该网格中找到相交点的可能性越大，但进行相交测试的计算量也越大；当网格划分较小时，在单个网格中相交测试计算量小，但找到交点的可能性也小，同时为寻找下一邻居网格需要进行网格线相交测试。

2.2 建筑物归类

网格划分后，必须准确判断建筑物所在网格，否则将导致误差甚至出现错误。判断建筑物所在分区有如下三种方法：

1）中值法：建筑物的边构成线段，求线段两个端点所在网格并记录。求线段中点所在网格，若未被记录，继续细分中点，直到所有中点所在分区都被记录。

2）遍历法：建筑物的边构成线段，与所有的网格边界求交点，并判断交点所在网格，得到建筑物所在分区。

3）扩大检验法：先求出墙面两端点所在网格，以这两网格相距最远的两个顶点为顶点组成的矩形所覆盖的网格都认为含有该墙面，得到交点后要检验交点所在网格号是否与墙面所在网格号一致。

中值法速度快但误差较大；遍历法可保证100%准确但遍历时间较长；扩大检验法可保证100%准确且运算速度较快，故本文采用了该方法对墙面进行分类。另外，对于传播场景中的反射线和透射线，只需要将其视为新的射线，也可以运用本文加速算法进行相交测试，所以实际中不需要区分轴线的属性（直射线，反射线还是透射线）。

3 数值仿真及分析

不失一般性以COST231组织提供的慕尼黑城市场景数据［12］对本文模型进行验证，该数据库包含了整个城市建筑物分布和墙面坐标，同时还提供三条实测路径数据作为理论参考。

表2 仿真参数表

慕尼黑城市测试场景长2 400m，宽3 400m，包括建筑物2 088座和墙面17 445面（如图3所示），表2给出了测试和仿真参数，其中λ表示波长，波束数目（即轴线数目）由高斯波束宽度决定。

图3 慕尼黑城市场景和测试路径

场景网格划分越大，在该网格中找到相交点的可能性越大，但在网格中进行相交测试的计算量也越大；反之，在网格中进行相交测试的计算量虽小，但轴线跨越的网格数将大大增加。图4比较了L＝100λ时，不同网格大小对仿真时间的影响，由图可见二维网格过大或过小耗时均会增加，对于慕尼黑场景而言，网格取50m×50m时预测耗时最短。在该仿真参数下，表3给出了网格为50m×50m时，有加速算法和无加速算法的效率比较，由表可见采用网格加速算法后预测效率可提高约50倍，大大减少了预测时间。

图4 网格大小与仿真时间关系

表3 归一化运算耗时比较

轴线数目越多，预测结果精度越高，但计算量会相应增加；轴线数目越少，计算量相应减少，但精度会下降，实际中需要选取合适的轴线数达到运算量与精度的平衡。图5给出了50m×50 m网格，高斯波束宽度分别取50λ和100λ时预测值与实测结果比较。由图可见：1）当L＝50λ时，轴线数较少为14 750条，预测精度稍差；2）当L＝100λ时，轴线数为44 521，仿真结果与实测值基本一致。部分区域仍存在误差的主要原因可能为：实测数据受场景中的车辆、行人、树木等因素的影响，而这些因素无法在场景数据中体现。

表4比较了本文模型与其他模型在慕尼黑场景中电波传播损耗预测精度，表中STD（标准差）和MEAN（均值）分别表示预测值与实测值之差的均方差以及平均值，其他模型性能参数来自文献［13］。由表可见：1）确定性模型精度比实测统计模型精度高；2）本文模型与传统射线跟踪模型预测精度基本相当，优于实测统计型模型。

表4 本文模型与其他模型性能比较

4 结 论

本文提出了一种基于三维高斯波束跟踪的传播损耗预测改进模型，该模型将源场分解为一系列高斯波束，并利用几何光学原理处理复射线的跟踪。相比传统射线跟踪方法，该方法预处理简单，对所有波束可进行统一处理而无需考虑接收点的具体位置和绕射效应，可大大简化实际问题的处理。同时，文中还提出了一种基于网格的加速算法，该算法无需对建筑物做过多的预处理，易于实现。针对慕尼黑城市环境的预测结果表明，该方法不降低精度且预测效率是原来的数十倍，可用于辅助无线网络的规划、设计和优化。

［1］CASTRO B S L，GOMES I R，RIBEIRO F C J，et al.COST231－Hata and SUI models performance using a LMS tuning algorithm on 5.8GHz in Amazon region cities［C］//IEEE Proceedings of the Fourth European Conference on Antennas and Propagation.Barcelona，Spain，April，2010：1－3.

［2］NISIRAT M A，ISMAIL M，NISSIRAT L，et al.A Hata based model utilizing terrain roughness correction formula［C］//The 6th International Conference on Telecommunication System，Services and Applications.Indonesia，October，2011：284－287.

［3］ESPARZA F，TORRES V，BERUETE M，et al.Simulation of indoor LTE behaviour［C］//Proceedings of the fourth IEEE European Conference on Antennas and Propagation.Barcelona，April，2010：1－3.

［4］李超峰，焦培南.三维射线跟踪预测模型在5.8GHz的实验验证［J］.电波科学学报，2006，21（6）：921－924.LI Chaofeng，JIAO Peinan.Experimental verification of a ray tracing model at 5.8GHz［J］.Chinese Journal of Radio Science，2006，21（6）：921－924.（in Chinese）

［5］程 勇，吴剑锋，曹 伟.一种用于移动系统场强预测的准三维射线跟踪模型［J］.电波科学学报，2002，17（2）：151－158.CHENG Yong，WU Jianfeng，CAO Wei.A quasi 3－D ray－tracing model for field prediction in mobile systems［J］.Chinese Journal of Radio Science，2002，17（2）：151－158.（in Chinese）

［6］刘海涛，黎滨洪，谢 勇，等.并行射线跟踪算法及其在城市电波预测的应用［J］.电波科学学报，2004，19（5）：581－585.LIU Haitao，LI Binhong，XIE Yong，et al.Parallel ray－tracing algorithm and its application for propagation prediction in urban microcellular environments［J］.Chinese Journal of Radio Science，2004，19（5）：581－585.（in Chinese）

［7］FLUERASU A，LETROU C.Gaussian beam launching for 3Dphysical modeling of propagation［J］.Annals of telecommunications，2009，64（11/12）：763－776.

［8］GHANNOUM I，LETROU C，BEAUQUE G.Frame based Gaussian beam bouncing［C］//IEEE UESI International Symposium on Electromagnetic Theory.Berlin，August，2010：68－71.

［9］KATSAV M，HEYMAN E.A beam summation representation for 3－D radiation from a line source distribution［J］.Antennas and Propagation，2008，56（2）：602－605.

［10］TAHRI R，FOURNIER D，COLLONGE S，et al.Efficient and fast Gaussian beam－tracking approach for indoor－propagation modeling［C］//IEEE Picture Coding Symposium.Nagoya，December，2010：122－125.

［11］彭群生，鲍如军，金小刚.计算机真实感图形的算法基础.北京：科学出版社［M］，1991：162－169.

［12］Mannesmann Mobilfunk GmbH. Urban micro cell measurements and building data［EB/OL］.［2012－6－28］.http：//www2.ihe.uni－karlsruhe.de/forschung/cost231/cost231.en.html.

［13］CICHON D J，KURNER T.Propagation prediction models digital mobile radio toward future generation system［EB/OL］.［2102－6－28］.http：//www.lx.it.pt/cost231/.