无刷直流伺服驱动系统设计

陈 玄

（中北大学 电工学综合实验室 山西太原 030051）

0 引言

伴随着现代工业的快速发展，标志着一个国家工业实力的相应设备如精密机床、工业机器人等对其“驱动源”——电伺服驱动系统提出了越来越高的要求。而基于正弦波反电势的永磁同步电动机（简称PMSM）因其卓越的性能已日渐成为电伺服系统执行电动机的“主流”。然而伺服控制技术是决定交流伺服系统性能好坏的关键技术之一，是国外交流伺服技术封锁的主要部分。随着国内交流伺服电机及驱动器等硬件技术逐步成熟，以软形式存在于控制芯片中的伺服控制技术成为制约我国高性能交流伺服技术及产品发展的瓶颈。研究具有自主知识产权的高性能交流伺服控制技术，尤其是最具应用前景的永磁同步电动机伺服控制技术，具有重要的理论意义和实用价值。

1 直流无刷电动机工作原理

直流无刷电动机结构原理如图1所示。它主要由电动机本体、位置传感器和电子开关线路3部分组成电动机本体在结构上与永磁同步电动机相似，但是没有笼型绕组和其他启动装置[1]。其定子绕组一般制成多相(三相、四相、五相不等)，转子由永久磁钢按一定极对数（2P=2，4，…）组成。

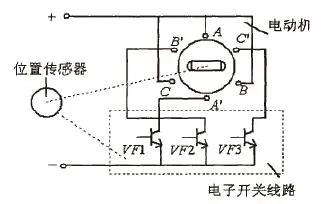
图1 直流无刷电动机结构原理图

直流无刷电动机是一个由电动机本体、功率主回路以及转子位置传感器等部分组成的闭环系统。位置传感器主要功能是保证电动机定子绕组准确换向，确保直流无刷电动机在运行过程中定转子两磁场始终保持基本上垂直，以提高其运行效率[2]。

2 直流无刷电机伺服系统的模糊自适应PID控制

2.1 模糊控制基本原理

模糊控制的基本原理框图如图2所示，模糊控制系统主要由输入/输出接口、模糊控制器、执行机构、受控对象和检测装置等5个部分组成[3]。核心部分是模糊控制器。

图2 模糊控制基本原理框图

2.2 模糊控制器设计

模糊控制器的结构，所采用的模糊规则、模糊逻辑推理算法以及模糊决策的方法等都直接影响到模糊控制系统的性能优劣。

模糊控制器的组成框图如图3所示。主要包括：输入量模糊化、数据库、规则库、模糊推理机和反模糊化等5个部分[4]。

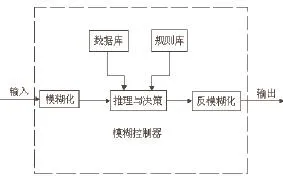
图3 模糊控制器组成框图

2.3 数字式PID控制算法的改进

位置式PID控制算法和增量式PID控制算法是两种标准的PID控制。在使用过程中，由于执行机构、被控对象、工业环境、控制要求等个方面的原因，标准的PID控制往往不能满足要求，因此必须对PID控制控制算法进行改进。用计算机实现PID控制，可以根据系统的实际要求，对PID控制算法进行灵活改动，达到提高调节品质的目的。积分项的改进算法：

(1)积分分离

PID控制中，积分控制的主要作用是消除稳态误差。但是，当外部扰动较大或是大幅度地改变给定值时，由于此时有较大偏差及系统有惯性和滞后，故在积分控制作用下，往往会产生较大的超调和长时间的波动。对于温度、成分等变化缓慢的过程，这一现象尤为严重。因此，在误差较大的阶段，完全可以先不投入积分控制，以比例控制为主(可根据实际情况决定是否采用微分控制)，利用比例控制产生比较大的控制作用，迅速地将误差减小。当误差减小到一定程度后，再将积分控制投入，从而达到完全无误差，这就是所谓积分分离。

其基本算法如下：首先给定误差限∆e。当e(n)＞∆e时，使用PID控制，当e(n)＜∆e时，使用PID控制。下面简要推导PID控制时的算。将式

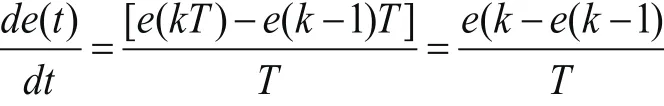
（式中：T-采样周期;K--采样序号）去掉积分项后得

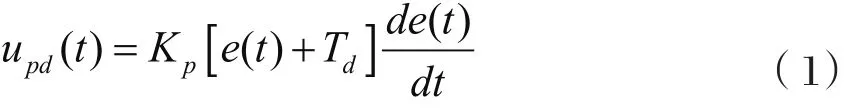
离散化后得

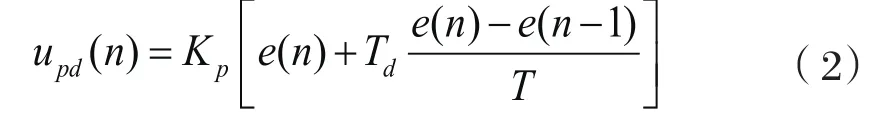
一般来说∆e的选择比较重要，选择得太大，达不到积分分离的作用，选择得太小，则有可能比例控制的无法使系统的误差进入的区域。

如果选择实际微分PID算法，则可以去掉∆ ui( n)得

得

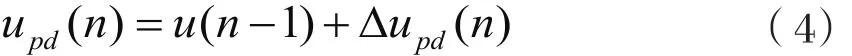
(2)消除积分不灵敏区

在实际微分PID控制算法中，其积分控制算法的增量计算的：

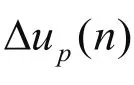
当Sk大于字长精度后，再输出Sk，从而可以确保消除残差。

3 基于matlab的转速控制系统构建与PID设计

3.1 基于MATLAB的BLDC系统模型的建立

在MATLAB7.0的Simulink环境下，利用SimPowerSystemToolbox2.3丰富的模块库，在分析BLDC数学模型的基础上，提出了建立BLDC控制系统仿真模型的方法，系统设计框图如图4所示。

如图4所示，BLDC建模仿真系统采用双闭环控制方案：转速环由PI调节器构成，电流环由电流滞环调节器构成。根据模块化建模的思想，将图4所示的控制系统分割为各个功能独立的子模块，图5即为BLDC建模的整体控制框图，其中主要包括：BLDC本体模块、电流滞环控制模块、速度控制模块、参考电流模块、转矩计算模块和电压逆变模块。通过这些功能模块的有机整合，就可在Matlab/Simulink中搭建出BLDC控制系统的仿真模型，并实现双闭环的控制算法，如图5所示，图中各功能模块的作用与结构简述如下。

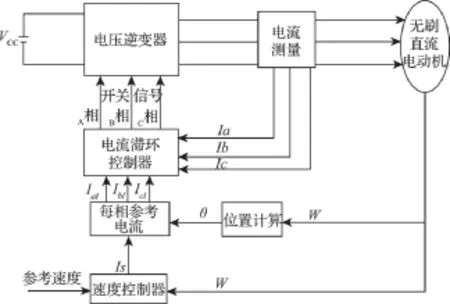
图4 BLDC控制系统仿真建模组成框图

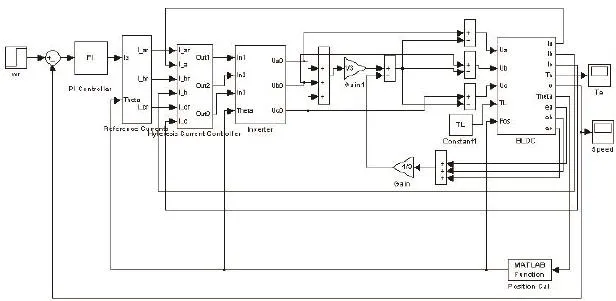
图5 MATLAB/Simulink中BLDC仿真建模整体控制框图

3.1.1 BLDC本体模块

在整个控制系统的仿真模型中，BLDC本体模块是最重要的部分，该模块根据BLDC电压方程式求取BLDC三相相电流，控制框图如图6所示。由电压方程式可得，要获得三相相电流信号ia、ib、ic，必需首先求得三相反电动势信号ea、eb、ec[5-6]。

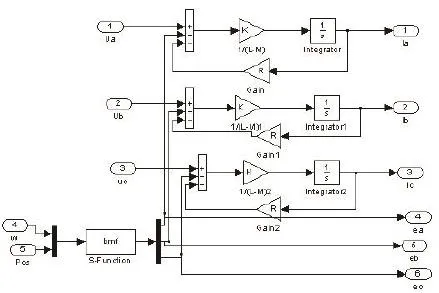
图6 BLDCM本体模块结构框图

而BLDC建模过程中，梯形波反电动势的求取方法一直是较难解决的问题，反电动势波形不理想会造成转矩脉动增大、相电流波形不理想等问题，严重时会导致换向失败，电机失控。因此，获得理想的反电动势波形是BLDC仿真建模的关键问题之一。目前求取反电动势较常用的三种方法为：(1)有限元法，这种方法以变分原理为基础，将电磁场理论与磁路等效模型相结合，根据微分方程及边界条件，求解有限元方程组，得到节点上的位函数，建立反电动势的波形。应用有限元法求得的反电动势脉动小，精度高，但方法复杂、专业性强、不易推广。(2)傅里叶变换(FFT)法，BLDC理想的梯形波反电动势波形中含有大量的高次谐波分量，采用FFT方法，通过各次谐波叠加可得到近似的梯形波反电动势，FFT法应用简单，但需要进行大量三角函数值的计算，对仿真速度影响较大。(3)分段线性法，如图7所示，将一个运行周期0～360°分为6个阶段，每60°为一个换向阶段，每一相的每一个运行阶段都可用一段直线进行表示，根据某一时刻的转子位置和转速信号，确定该时刻各相所处的运行状态，通过直线方程即可求得反电动势波形。分段线性法简单易行，且精度较高，能够较好的满足建模仿真的设计要求。因而，本文采用分段线性法建立梯形波反电动势波形。

图7 电流滞环控制模块结构框图

3.1.2 电流滞环控制模块

电流滞环控制模块的作用是实现滞环电流控制方法，输入为三相参考电流和三相实际电流，输出为逆变器控制信号，模块结构框图如图7所示。当实际电流低于参考电流且偏差大于滞环比较器的环宽时，对应相正向导通，负向关断；当实际电流超过参考电流且偏差大于滞环比较器的环宽时，对应相正向关断，负向导通。选择适当的滞环环宽，即可使实际电流不断跟踪参考电流波形，实现电流闭环控制。

3.1.3 速度控制模块

速度控制模块的结构较为简单，如图8示，单输入：参考转速和实际转速的差值，单输出：三相参考相电流的幅值Is。其中，Ki为PI控制器中P（比例）的参数，K/Ti为PI控制器中I（积分）的参数，Saturation饱和限幅模块将输出的三相参考相电流的幅值限定在要求范围内。

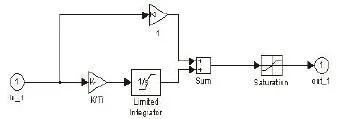
图8 速度控制模块结构框图

3.2 MATLAB的PID控制器设计

3.2.1 PID参数整定

现在一般采用的是临界比例法。利用该方法进行 PID控制器参数的整定步骤如下：

(1)首先预选择一个足够短的采样周期让系统工作；

(2)仅加入比例控制环节，直到系统对输入的阶跃响应出现临界振荡，记下这时的比例放大系数和临界振荡周期；

(3)在一定的控制度下通过公式计算得到PID控制器的参数。

PID参数的设定：是靠经验及工艺的熟悉，参考测量值跟踪与设定值曲线，从而调整PID的大小。 比例I/微分D=2，具体值可根据仪表定，再调整比例带P，P过头，到达稳定的时间长，P太短，会震荡，永远也打不到设定要求。

PID控制器参数的工程整定,各种调节系统中P.I.D参数经验数据以下可参照：

温度T: P=20～60%,T=180～600s,D=3～180s

压力P: P=30～70%,T=24～180s

液位L: P=20～80%,T=60～300s

流量L: P=40～100%,T=6～60s

3.2.2 基于MATLAB的PID仿真

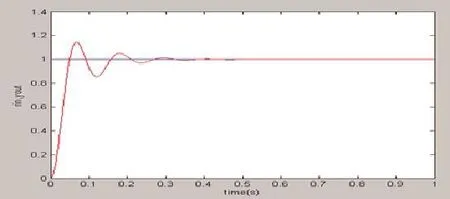
图9 原始PID仿真图

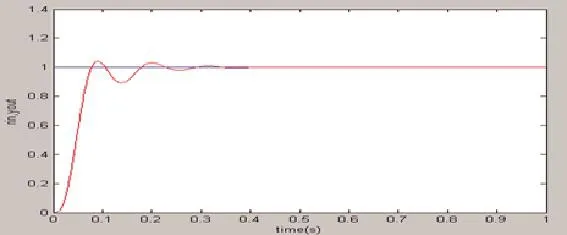
图10 加增量限幅后的PID仿真图

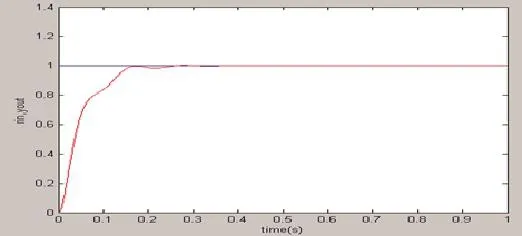
图11 加积分分离和增量限幅后PID仿真

图12 积分分离、增量限幅和变速积分后的PID仿真图

给PID输入一个阶跃响应时从图9～图12可以逐渐发现，在采用不同的算法改进后，输出曲线慢慢稳定。通过分析这些算法，能够得出当PID仿真图9出现超调量过大的时加入增量限幅可以很快将超调量缩小到图9所示；然而输出曲线仍然在0 s～0.4 s处波动，为了解决这一问题，在增量限幅偶后再加上积分分离，仿真得到图11；为了进一步使PID输出达到满意的效果，对算法再进行改进，加入变速积分，仿真得到图12，从图12已经可以很好地实现对控制对象进行稳定输出，从而使得转速值在期望范围内。

4 结论

模糊控制是智能控制的一种，具有较强的鲁棒性，且算法简洁，实时性较强，应用很广泛。针对永磁无刷直流电机伺服系统被控对象非线性、系统参数时变性等特点，设计了一种简单有效的、能自适应调整PID参数的无刷直流电机伺服系统模糊自适应PID位置伺服控制器。仿真结果证明所设计的位置控制器能使无刷直流电机伺服系统达到较高的定位控制精度。

综合上述仿真结果，我们可以看出用改进的PID算法可以更稳定的对无刷直流电机的转速实现控制。

[1]田淳.无位置传感器稀土永磁无刷直流方波电机调速系统[C].第五届中国直流电机调速传动学术会议论文集,1997.

[2]吴捷.永磁无刷伺服电机无传感器位置法[J].微特电机,2000(4).

[3]李久胜,王炎.基于滑模原理的鲁棒交流伺服控制器[J].哈尔滨工业大学学报,2000,32(2):19-23.

[4]王传忠,杨霞,李强.专家一模糊滑模变结构控制伺服系统的研究[J].河北工业大学学报,2001,30(5):52-55.

[5]奏忆.现代交流伺服系统[M].武汉:华中理工大学出版社,1995.

[6]陈世坤.电机设计[M].北京:机械工业出版社,1997.

[7]李友善,李军.模糊控制理论及其过程控制中的应用[M].北京:国防工业出版社,1993.

[8]刘金馄.先进PID控制及其MATLAB仿真[M].北京:电子工业出版社,2003.