焊缝自动跟踪系统的Fuzzy-PID复合控制技术

尹 懿，叶建雄，张丽玲

（南昌工程学院 机械与电气工程学院，江西 南昌 330099）

0 前言

大量的工业机器人应用于焊接领域，拥有焊缝自动跟踪系统的自动化焊接系统大大提高了焊接生产效率和产品质量[1]。由于焊接过程具有特殊性，常表现为复杂非线性系统，难以建立适当的数学物理模型，传统的控制方法已不能满足要求。因此，在自动焊接过程中如何模仿人类特有的智能来实现复杂的焊接控制是目前和将来焊接自动化研究的重要内容[2]。模糊控制器具有能适应被控对象非线性和时变性的优点，且鲁棒性好[3]。但其稳态控制精度较差，控制不够细腻，难以达到较高的控制精度，尤其在平衡点附近。此外，它缺少积分控制作用，不易消除系统的静差。为弥补这些缺陷，实践中常将基本模糊控制器与其他控制器相结合，充分发挥其各自优点，使控制效果更加完美。因此，把PID控制策略引入Fuzzy控制器，构成Fuzzy-PID复合控制，是改善控制性能的一种途径。

1 光电传感器

所采用的光电传感器是利用光电元件检测人工辅助线，根据偏差情况输出相应的偏差信号[4]。光电传感器共有三只普通小电珠和三只光敏管，小电珠发出光照射到钢板上，反射回来后又照射到光敏三极管，人工辅助白线上方的光敏管输出的电流较其余光敏管要大，由此可知焊缝的偏差情况。通过实验得到了传感器输出焊缝偏差的数据。实验结果如表1所示。

表1 焊缝偏差实验结果

分析表1中的数据，发现中值滤波后，可采用一种简单的加权比较方法将焊缝的偏差情况反映出来。

式中 Sd为焊缝偏差输出信号，其符号代表方向；SL为左光敏管输出信号；SR为右光敏管输出信号；SM为中间光敏管输出信号。结果显示，凡存在偏差时均小于1，因此，以±1为阈值判断是否存在偏差，可以将传感器精度控制在±1 mm内。

2 控制系统的分析与建立

2.1 跟踪系统控制原理

所研究的焊缝跟踪系统为传感器前置式焊缝跟踪系统，传感器的检测点与焊接点有一固定的距离，系统存在一固有偏差，为消除该偏差，有两种方案可实现[5-6]：

（1）在坡口中心与导轨间的距离变化不太大的情况下，把传感器本体与焊炬跟踪执行机构固定连接在一起。

（2）传感器与焊炬分别由两套执行机构独立驱动，即对传感器进行实时调整，然后延迟固定的时间，让焊炬执行机构做完全相同的随动。

第一方案简化了执行机构，但对传感器提出了更高的要求，控制系统较复杂，增加了控制难度；第二方案则降低了对传感器的要求，但如采用两套十字滑块将大大增加系统的成本，因此，采用一套旋转机构代替一套十字滑块，即焊炬固定在十字滑块上，旋转机构也固定连接在十字滑块上，并可以绕一固定点旋转摆动，传感器则固定在旋转机构上。在焊缝跟踪过程中，传感器在前对焊缝进行实时跟踪，经过一段时间的延迟后，执行机构再调节焊炬的位置，使焊炬沿传感器行走的轨迹行走，从而实现焊缝跟踪[7]。

焊缝跟踪系统控制结构如图1所示，包括传感器、计算机控制系统和调节执行机构三部分。

图1 焊缝跟踪系统结构

2.2 焊缝跟踪过程分析与数学模型

焊缝跟踪过程如图2所示，设焊缝曲线为R（t），表示为系统的输入量，传感器调节曲线Y1（t）与焊炬调节曲线Y2（t）为系统的输出量。

图2 焊缝跟踪过程示意

纵坐标y表示各曲线相对导轨的偏差量，横坐标x表示传感器沿导轨行走的距离，t为相应的行走时间。传感器前置，前置量为λ。若焊接速度（即焊接小车沿x轴行走的速度）为v，焊炬滞后传感器的时间τ=λ/v，O点为焊接起始点。设焊炬在A点时，传感器的位置点在B点，与A点相距λ，此时有

式中S1（t）为传感器执行机构跟踪的执行量；S2（t）为焊炬执行机构跟踪的执行量。

传感器执行机构跟踪的执行量应该是一角度α，传感器与焊缝的偏差为λtan α，由于传感器单步旋转的角度α不大，近似等于tan α，即认为传感器与焊缝的偏差为λα，将其作为焊炬的执行量。当这种误差累积到1 mm时，传感器将检测到这种误差并作出相应调整，不会造成较大的累积误差。传感器执行机构跟踪的执行量与焊炬执行机构跟踪的执行量存在一比例放大的关系，放大系数为λ。为了简化模型，在推导过程中设λ=1，而实际应用时则通过调节执行机构的执行量来适应不同的λ。当焊炬在A点、传感器在B点时，因此，传感器检测的偏差数据实际上是传感器所在位置（即检测点B）相对于焊炬所在位置（即焊接点A）的偏移量，故有

从实际来看，e（t）为传感器与导轨之间偏转的角度。又设ΔS（τ）为焊炬从t～t+τ时的调节量，有

在t时刻，传感器检测点与焊缝中心的实际误差e1（t）为

焊炬经过τ时间行走以后，与传感器检测点的实际误差e2（t）为

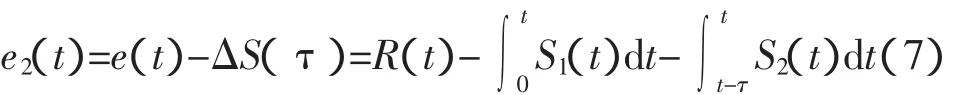
以e1（t）和e2（t）作为控制量对系统进行控制。

上述各式可用结构图表示，如图3所示。其中，G1（t）为传感器执行机构传递函数；G2（t）为焊炬执行机构传递函数；S1（t）为传感器执行机构跟踪的输出量；S2（t）为焊炬执行机构跟踪的执行量；R（t）为系统的输入量；Y1（t）为传感器调节输出量；Y2（t）为焊炬调节输出量。

将上述时域内表示的关系经过拉普拉斯变换，可得到如图4所示的跟踪系统结构框图。

图3 焊缝跟踪系统运动关系结构框图

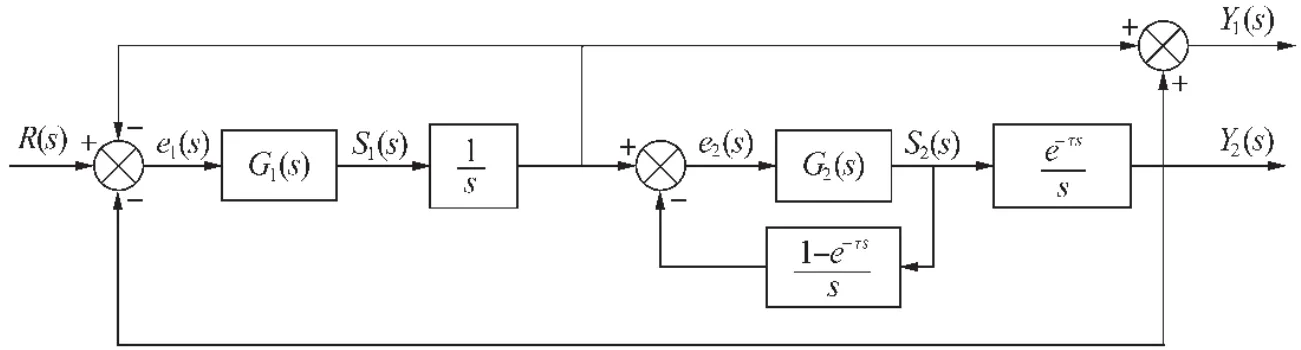
图4 焊缝跟踪控制系统结构框图

3 Fuzzy-PID复合控制器设计

常规二维模糊控制器是以误差和误差变化率为输入量，具有比例-微分控制作用。比例控制可提高系统响应速度，减小系统稳态误差；微分控制则使系统超调量减小，稳定性增加，但对于干扰同样敏感，导致系统抗干扰能力降低。模糊控制器缺少积分作用，使其消除系统误差能力欠佳，难以达到较高的控制精度。如模糊控制器在平衡点附近就存在盲区，虽然可依据Mamdani法则设置的隶属函数分布有意避开零点，可即使这样，零点左右两个相邻模糊子集的核之间，仍有一定的“空白”区，平衡点附近依然存在死区。

二维模糊控制器有偏差和偏差变化率两个分量，这就相当于PID控制器中比例和微分两环节，但缺乏积分环节。积分控制可消除稳态误差，这是模糊控制器所缺乏的。虽然积分控制的动态响应慢，但可以用动态响应快的比例控制环节弥补。如果把比例、积分控制联合起来组成PI控制，既能获得较高的稳态精度，又能具有较快的动态响应。为弥补模糊控制器（简称Fuzzy控制器或F控制器）在平衡点附近出现的盲区缺陷，可引入PI控制环节，与模糊控制器构成Fuzzy-PID复合控制器。

在输入信号e之后，设置一带阈值的模态转换器，根据阈值与e的比较结果确定模态：当e大于阈值时，信号传输至Fuzzy控制器，以获得良好的动态性能；当e小于阈值时，则信号传输到PI控制器，以获得良好的稳态性能。该复合控制器与单一模糊控制器相比具有更高的稳态精度，消除了盲区；与经典PID控制器相比，则具有更快的动态响应特性。

因此，本系统采用Fuzzy-PID控制，在较大偏差范围时采用模糊控制，在较小偏差范围时则采用PID控制，两种控制方式的转换依据预先确定的偏差阈值来实现，在此设定的阈值为2 mm。

4 仿真与分析

为检验系统模型与控制器的性能，采用Matlab软件的Simulink软件包对系统进行了仿真。分别建立了Fuzzy-PID控制系统和经典控制系统的仿真模型，为不失一般性，执行机构均采用二阶惯性系统，设系统的时间常数为50 ms，滞后时间τ=0，焊炬动作延迟时间为20 s。仿真结果如图5所示。图中，A为传感器的响应曲线，B为焊炬的响应曲线。系统的性能主要取决于焊炬的情况，因此，考察系统性能指标也就是看焊炬的响应曲线。

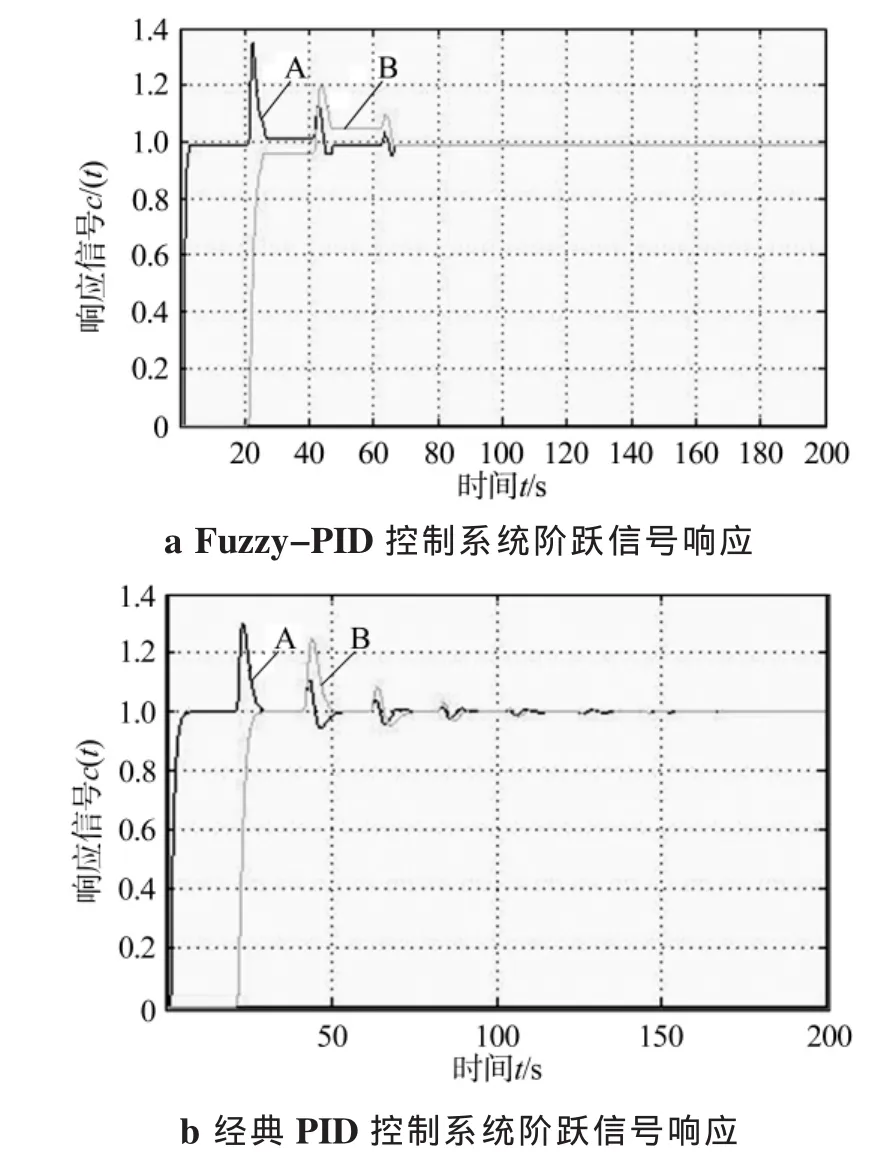
图5 仿真结果

其中，Fuzzy-PID控制系统上升时间tr=6 s，超调σ%=20%，振荡次数N=2（稳态误差取2%，以下同），稳态误差小于1%。如图5a所示。经典PID控制系统上升时间tr=6 s，超调σ%=25%，振荡次数N=4，稳态误差小于1%。如图5b所示。从仿真结果可看出，Fuzzy-PID控制系统的动态性能指标优于经典控制系统，静态性能指标与之相差无几，Fuzzy-PID控制系统比经典控制系统更加稳定。

5 实际焊接跟踪效果与分析

为检验所研制的焊缝跟踪系统是否达到设计要求，进行了实际焊接跟踪实验。焊接跟踪实验结果如图6所示。

图6 实际焊接跟踪效果

实验表明，所研制的焊缝自动跟踪系统可以满足一般情况下的焊接要求，最大误差为1 mm。其中，斜线因其具有固定的斜率，因而焊缝偏差相差不大，精度较高。而折线焊缝在转角处有较大的偏差角度，因传感器前置和执行系统惯性等原因，此处产生的偏差及偏差变化均较大，跟踪精度在转折点较低，而且偏转角度越大，跟踪精度越低。

产生的误差主要有：

（1）传感器精度误差。传感器本身存在着误差，本文所采用的光电传感器精度误差为±1 mm以内。

（2）控制误差。虽然Fuzzy-PID控制的效果比经典控制好，但是也存在误差。

（3）执行机构误差。执行机构接收到控制系统输出的调节量之后，没有调节相应的距离，即存在着执行调节误差。

（4）定位误差。焊枪在初始定位时如果与焊缝中心不重合，就会存在定位偏差。

6 结论

（1）提出了一种附加传感器式焊缝跟踪系统的理论模型，并在理论分析该模型的基础上，设计了Fuzzy-PID控制系统并对其进行了仿真。研究表明，该模型结构简单、成本低，Fuzzy-PID控制系统提高了系统的精度和稳定性。

（2）实验结果表明，研制的焊缝自动跟踪系统可对无坡口对接接头斜线和折线焊缝进行自动跟踪，跟踪精度满足一般工业焊接的要求。

[1]Bob Irving.Sensors and Controls Continue to Close the Loop in Arc Welding[J].Welding Journal，1999,78(4)：31-36.

[2]Murakami S，Takemoto F，Fujimura H，et al.Weld-line Tracking Control of Arc Welding Robot Using Fuzzy Logic Controller[J].Fuzzy Sets and System，1989，32(2)：221-237.

[3]Salim Labiod，Mohamed Seghir Boucherit，Thierry Marie Guerra.Adaptive Fuzzy Control of a Class of MIMO Nonlinear Systems[J].Fuzzy Sets and System，2005,152(3)：651-664.

[4]尹 懿，洪 波，黄 俊，等.用于焊缝跟踪光电传感器的研究[J].仪表技术与传感器，2005(9)：6-8.

[5]蒋力培，张甲英，马宏泽.传感器超前检测式焊缝自动跟踪系统的控制模型[J].焊接学报，1998，19(3)：184-189.

[6]叶建雄，张 华.旋转电弧水下药芯焊丝电弧焊的智能化焊接系统[J].焊接学报，2008，29(3)：141-144.

[7]尹 懿，洪 波，张晨曙，等.光电传感器式焊缝自动跟踪系统[J].焊接学报，2006，27(9)：93-98.