V-H荷载空间中桩基破坏包络线特性数值分析
徐 超
(中铁大桥勘测设计院集团有限公司,湖北武汉 430000)
桩基承受组合荷载作用问题在港口码头、桥梁、支挡建筑、高耸塔型建筑及近海钻采平台等工程中经常遇到。如何合理地评价组合荷载作用下的桩基础承载力,关系到建筑物的安全和优化设计,对整个基础工程的投资也起着控制作用。
桩基在轴向和横向同时作用下极限承载力目前主要有承载力修正系数法[5]和破坏荷载包络线法。
桩基破坏荷载包络线确定极限承载力的方法,Meyerhof等人做了大量的工作,提出了确定倾斜荷载下桩基极限承载力的半经验公式[1-3],但限于试验条件,仅仅对少数荷载倾角进行了研究,未能反映桩基破坏包络线的整体轮廓。为进一步研究V-H荷载空间中桩基破坏包络线的特性,对荷载倾角分别为0°、10°、20°、30°、45°、60°以及 90°等 7 种工况进行研究,并探讨了荷载加载方式对桩基破坏包络线的影响。
1 极限承载力取值
倾斜荷载-桩顶合成位移(水平和竖向)曲线法确定基桩的极限承载力,是将曲线开始变为直线或基本为直线的那一点作为基桩的极限承载力。
图1为数值模拟计算得到的倾斜荷载Qθ-桩顶合位移s曲线。桩体假设为弹性体,桩身结构不会发生强度破坏,桩基失稳主要由于地基土发生塑性屈服造成。为了反映桩基失稳机理,采用位移控制极限承载力取值方法,并规定把桩顶合位移150 mm(桩径的10%)对应的倾斜荷载作为基桩的极限承载力Qθu(见表1)。

图1 倾斜荷载Qθ-桩顶合位移s曲线
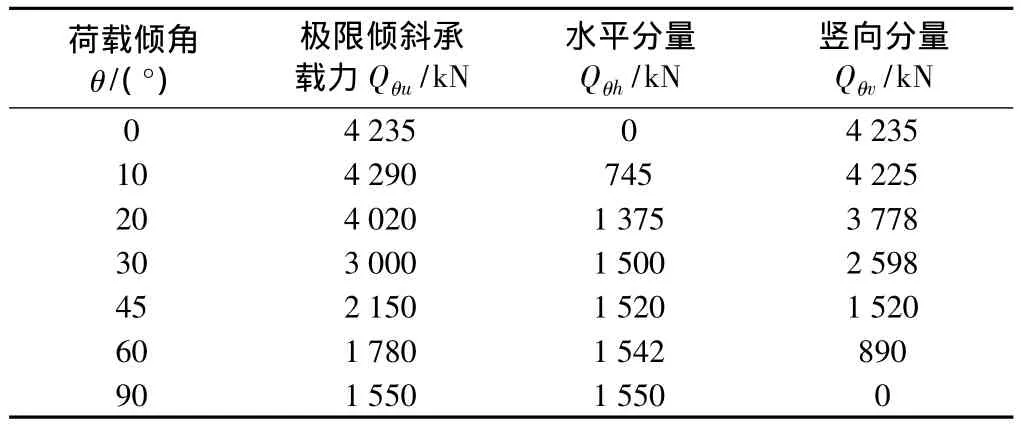
表1 倾斜荷载下桩基的极限承载力
2 桩基破坏包络线特性
根据表1求得的屈服荷载,可以确定V-H荷载面上的屈服点。图2为桩基在V-H荷载面中的屈服点分布,将所有的屈服点连接便可得到组合荷载作用下桩的承载力屈服包络线。
在荷载倾角θ=0°情况下,桩顶发生150 mm沉降,竖向荷载达到4 235 kN,约占极限竖向承载力的92%。

图2 V-H荷载空间桩基屈服包络线
在荷载倾角θ=10°情况下,桩同时承受竖向和水平方向的荷载,水平方向的荷载使桩顶产生水平位移;较小荷载水平分量造成的桩前上部局部区域内土压力的增加对桩的竖向承载特性影响很微小,基桩的倾斜荷载-沉降曲线在荷载倾角θ=10°时与θ=0°差异不明显。因此,在桩顶合位移150 mm的控制下,荷载竖向分量仅比荷载倾角θ=0°情况下的竖向承载力小了5 kN,而荷载水平分量却发挥了桩极限水平承载力的48%。
在荷载倾角θ=20°情况下,桩顶发生的竖向位移不再占主要地位,桩身在较大荷载水平分量下水平位移增大很多,并且超过了竖向位移。在桩顶合位移达到150 mm情况下,荷载竖向分量约占极限竖向承载力的82%,荷载水平分量占极限水平承载力的89%。从图2中也可以发现,θ=20°对应的屈服点是包络线上一个特征点,屈服点从(0,Qv)到(Qh,0)的轨迹(即包络线)在特征点处陡降。包络线上的特征点是桩基破坏机理随荷载倾角变化而发生变化的体现。
荷载倾角θ由30°变化到90°时,基桩水平位移占合位移的比重逐渐加大,荷载主要由桩身(抗弯能力)和上部桩前土体承担,桩承受的荷载水平分量占极限水平承载力的比重由97%增加到100%。
通过上述分析发现,V-H荷载空间中桩基破坏包络线也如同浅基础一样,存在一特征屈服点,其对应的荷载倾角姑且定义为荷载临界角θcr,如图3所示。当荷载倾角θ小于θcr时,桩基的竖向承载能力决定桩基稳定性;当荷载倾角θ大于θcr时,桩基的水平承载能力决定桩基稳定性;当荷载倾角θ在θcr附近变化时,桩基的稳定性由竖向和水平承载能力共同决定。
3 与前人研究成果比较

图3 V-H荷载空间中桩基破坏包络线示意
对Meyerhof等人23组倾斜因子的模型试验结果做统计分析(统计数据中极限承载力是Meyerhof按照合位移达到桩埋深的3% ~6%或转角达到1°~2°或倾斜荷载-合位移曲线上直线段起始点所对应的荷载)。统计数据荷载倾角主要集中在 0°、30°、45°、60°与90°。图4是倾斜因子的模型试验结果与经验公式的对比,图4中散点代表Meyerhof模型试验结果,点划线是Qh/Qv分别取0.0和1.0时的Koumoto经验公式计算结果。可以看出,Meyerhof经验公式用于估算极限倾斜荷载偏保守;统计数据大都落在Koumoto经验公式计算范围之内。因此选用Koumoto经验公式与数值试验结果做比较分析。

图4 文献倾斜因子统计分析
将数值模拟得到的Qh与Qv代入,Qh/Qv=0.37,利用Koumoto经验公式估算倾斜因子iθ。估算值与数值模拟所得的桩基破坏包络线和倾斜因子变化如图5所示。从图5中可以发现,利用Koumoto经验公式估算本文所研究的模拟桩倾斜荷载下基桩的极限承载力与数值计算结果相比,在荷载倾角小于30°时偏小,误差超过10%;在荷载倾角超过30°时偏大,误差在10%以内。
通过上述分析可以得出,①与Koumoto修正系数经验公式相比,Meyerhof包络线半经验公式估算极限倾斜承载力偏保守;②Koumoto修正系数经验公式和Meyerhof包络线半经验公式均不能反映出包络线的特征屈服点(即荷载临界角对应的屈服点),在临界角那一点估算出的极限承载力误差较大(17%和20%)。
4 结论

图5 数值计算与经验公式得到倾斜因子对比
通过V-H荷载空间中桩基破坏包络线特性问题进行数值研究,把桩顶合位移150 mm(桩径的10%)对应的倾斜荷载作为基桩的极限承载力,将数值计算结果与Meyerhof等人研究成果做比较,得出以下结论:
(1)V-H荷载空间中桩基破坏包络线存在一特征屈服点,屈服点对应的荷载倾角为临界角θcr。当荷载倾角θ小于θcr时,桩基的竖向承载能力决定桩基稳定性;当荷载倾角θ大于θcr时,桩基的水平承载能力决定桩基稳定性;当荷载倾角θ在θcr附近变化时,桩基的稳定性由竖向和水平承载能力共同决定。针对本文所研究的工况,θcr约为 20°。
(2)Koumoto经验修正系数和Meyerhof包络线半经验公式都不能反映出包络线上的特征屈服点(即荷载临界角对应的屈服点),在临界角那一点估算出的极限承载力误差较大(17%和20%);与Koumoto经验修正系数相比,Meyerhof包络线半经验公式估算极限倾斜承载力偏保守。
[1]胡人礼.桥梁桩基础分析和设计[M].北京:中国铁道出版社,1987
[2]范文田.轴向与横向力同时作用下柔性桩的分析[J].西南交通大学学报,1986,23(1):39-44
[3]赵明华.轴向和横向荷载同时作用下的桩基计算[J].湖南大学学报,1987,14(2):68-81
[4]李微哲.倾斜偏心荷载下基桩受力分析与室内模型试验研究[D].长沙:湖南大学,2005
[5]KOUMMOTOT,MEYERHOFGG,SASTRY,V V R N.Analysis of bearing capacity of rigid piles under eccentric and inclined loads[J].Canadian Geotechnical Journal,1986,23(2):127-131

