高速列车受电弓绝缘子的气动噪声计算及外形优化*
肖友刚,时 彧
(1.中南大学交通运输工程学院,湖南 长沙 410075;2.湖南科技大学 机电工程学院,湖南 湘潭 411201)
当列车高速行驶时,列车上的凹凸部位对气流产生了严重扰动,并使之产生复杂的流动分离及一系列的漩涡脱落及破碎,从而产生强大的外部空气脉动压力场,并转化成气动噪声[1-3]。借助声学比拟理论、低噪声风洞和阵列技术,确定了高速列车的主要气动噪声源[4-6]。受电弓作为车顶上的突出部件,气动噪声随列车运行速度增加而显著增大。为控制受电弓的气动噪声,日本相关科研机构进行了一系列实验和理论分析,研制了长形受电弓整流罩和低噪声受电弓[7-9],并在受电弓上使用多孔材料,取得了较明显的降噪效果[10]。受电弓整流罩将受电弓前的空气推向上方,从而减缓吹向受电弓的空气流,使受电弓附近的空气流速降低。由于气动噪声的能量约与流速的6次方成正比,因此,设置受电弓罩能显著降低气动噪声。但当行驶速度超过300 km/h时,受电弓罩分割空气流,在气流被分割的区域,会产生持续反复的涡流,这种涡流会使受电弓整流罩本身的噪声变大[11]。我国的高速列车建设虽然已取得了重大成果,但在受电弓整流罩和低噪声受电弓的研制上却比较滞后。目前,我国动车组上所用的受电弓构件数量多,棱角、空隙、台阶高差比比皆是,这些都会引起空气流的紊乱,导致各种不同尺度的漩涡形成、脱落及破碎,从而产生很大的气动噪声。而且该受电弓的构件尺寸小,产生的风鸣音频率高,因此,使用该受电弓对控制动车组的噪声不利。由于计算气动噪声对计算机软、硬件资源的要求高,针对该受电弓原型计算气动噪声很困难,因此,对该受电弓进行一系列简化,才有可能使计算得以进行,但这会使计算结果较大程度地偏离实际值。对单个部件进行计算,能取得理想的计算精度,其计算结果可指导设计,因此,只研究受电弓绝缘子的发声情况,为绝缘子的外形优化提供依据,为低噪声受电弓的设计提供思路。
1 受电弓绝缘子气动噪声预测理论
根据N-S方程和连续性方程,Lighthill导出了声传播方程[12]:

式中:ρ'为流体密度的扰动量,ρ'= ρ- ρ0;ρ与 ρ0分别是扰动与未扰动时的密度;Tij为Lighthill应力张量,Tij= ρuiuj- eij+ δij(p-ρ);eij为黏性应力张量;为声速。
Ffowcs Williams和Hawkings考虑运动固体边界的影响,按照Lighthill方程的推导方法,得出了Ffowcs Williams-Hawkings方程(简称 FW-H方程)[13]:

式中:vn为表面法向速度;δ(f)为Diracdelta函数;H(f)为Heaviside函数;Pij为表面应力张量。
式(2)中:方程右边第1项是Lighthill声源项,来源于物体周围流场内的Lighthill应力,为四极子声源项;第2项表示由表面脉动压力引起的声源,来源于物体的表面压力与粘性剪切应力,是偶极子声源项;第3项表示由表面加速度引起的声源,是单极子声源项。对于高速列车,其车身表面可以看作是刚性的,体积脉动量几乎为零,所以单极子声源项积分不必考虑;流场中四极子声源与偶极子声源强度之比正比于马赫数的平方,而高速列车的运动仍属于低速运动,如列车速度250 km/h时,其马赫数也仅为0.2左右,四极子源噪声相对较小,可略去不计。因此,偶极子源项的强弱和分布特性决定着其外部辐射声场的强弱及其分布规律。湍流场由不断发展的大小不同的涡旋构成,这种不断发展的不同尺度涡与湍流相互作用而产生不同频率的压力脉动,成为表面偶极子声源。大涡模拟(LES)对尺度大的湍流运动通过N-S方程直接计算,小尺度涡采用亚格子模型进行模拟,是目前计算湍流脉动较理想的方法。
将N-S方程进行空间过滤,得到不可压缩流体流动的LES控制方程:

为使方程(3)和(4)封闭,采用涡旋粘性模型构造τij的数学表达式。

采用大涡模拟(LES)模型和Smagorinsky-Lilly亚格子模型计算出流场边界脉动压力,再利用快速傅里叶变换(FFT)将流场中时域脉动信号变换成频域信号,获得气动噪声辐射场中的偶极子声源边界条件,进而计算出远场的辐射噪声。
2 高速列车受电弓绝缘子气动噪声的计算
2.1 受电弓绝缘子气动噪声的计算模型
动车组受电弓绝缘子的形状为圆形,高度为400 mm,直径为150 mm,如图1(b)所示。为了得出受电弓绝缘子的不同外形对气动噪声的影响规律,设计截面形状为矩形、椭圆形的绝缘子,矩形截面绝缘子的长为200 mm、宽为150 mm、高为400 mm,椭圆形截面绝缘子的长轴长为200 mm、短轴长为150 mm、高为400 mm,如图1(a),1(c)所示。动车组的每个受电弓有3个绝缘子,沿车顶中心线对称布置,如图2所示。假定矩形、椭圆形截面绝缘子的安装位置与圆形截面绝缘子的安装位置完全相同,且矩形的长边或椭圆的长轴平行于车顶中心线。参考低噪声受电弓绝缘子形状[9],设计图1(d)所示的绝缘子,该绝缘子截面形状为椭圆,长轴长为400 mm、短轴长为200 mm、高为800 mm。与低噪声受电弓绝缘子一样,假定拟设计的受电弓也只包括2个绝缘子,沿车顶中心线对称布置,长轴平行于车顶中心线。

图1 4种不同截面的受电弓绝缘子Fig.1 Four pantograph insulators with different sections

图2 动车组受电弓绝缘子的安装尺寸Fig.2 Mounting dimensions of EMU pantograph insulators
按照流域确定原则[14]及受电弓的外形尺寸,并考虑对称性,分别建立包含3个矩形截面绝缘子的LES模型(简称模型a)、包含3个圆形截面绝缘子的LES模型(简称模型b)、包含3个椭圆形截面绝缘子的LES模型(简称模型c)及包含2个椭圆形截面绝缘子LES模型 (简称模型d)。图3所示为车顶包含3个圆形截面绝缘子的LES模型,其他模型略。
在数值模拟计算中,一般采取有限计算域来代替无限计算域,选取正确的计算域边界对保证流场计算精度很重要。本研究中计算域速度入口边界应保证气流入口速度不受绝缘子影响,即气流在整个入口截面上速度分布均匀,将速度入口截面至绝缘子前端的距离设置为3 m;计算域截面边界应保证适当的阻塞比,将计算域截面顶端及侧边至绝缘子的距离均设置为2 m;为避免出口边界压力受到绝缘子的影响,将出口边界至绝缘子后端的距离设置为5m。绝缘子流场计算域如图3所示。计算边界条件设定如下:在入口截面ABCD处,采取速度边界条件,速度方向跟车速相反,速度根据车速确定,本研究中车速取300 km/h。在出口截面EFGH处,出口压力设定为大气压力,出口离绕流区较远,绕流对其的影响可以忽略。计算域左截面ABEF设置为对称边界,计算域底端BCGF及受电弓绝缘子表面按光滑壁面处理,采用无滑移边界条件,计算域顶端及右截面设置为无滑移边界。
采用六面体单元对计算域进行离散,离散后绝缘子表面的最大网格尺寸为5 mm,各计算模型的总网格数约为60万个。为了获得绝缘子表面丰富的边界层信息,对绝缘子表面网格进行了加密处理。

图3 包含3个圆形截面绝缘子的大涡模拟模型Fig.3 LES model with three circular section insulators
大涡模拟的计算条件:时间离散采用瞬态控制方式,空间离散优先采用基于节点的选项,求解方式选择分离隐式求解法,压力-速度耦合的修正采用PISO算法,压力离散格式采用压力交错法,动量离散格式采用BCD格式,模型的计算时间步设定为5000,时间步长选择0.5 s。
为了计算受电弓绝缘子在气流中的发声情况,选取受电弓绝缘子为发声体,距受电弓绝缘子后方2,4和6 m处,分别确定3个声监测点A,B和C,作为气动噪声的监测点,如图4所示。声场计算选择基于FW-H方程的声模拟方法,计算频率上限设定为1 kHz。
2.2 计算结果及分析
通过对计算结果进行后处理,得到列车运行速度为300 km/h时,A,B和C声监测点气动噪声的声压频谱,进一步分析得出A,B和C点在1/3倍频程中心频率处的A声级。将1/3倍频程中心频率处的声压级Lpi迭加,得到各监测点的总声压级LpF。迭加公式为[15]:

其中:LPi为声监测点在频率i处的A声级。

图4 气动噪声监测点的设置Fig.4 Monitoring points of aerodynamic noise
图5和图6所示分别是列车运行速度为300 km/h时,a~d模型中A,B和C监测点A声级的1/3倍频程频谱及总声压级,F是所研究频率的统称。从图5~6中可得出如下结论:
(1)气动噪声A声级的主要能量集中在80~800 Hz频率范围内,采用在该频段范围内隔声效果好的材料制作车身壁板,对降低车内气动噪声有利。
(2)在0~1000 Hz范围内,对模型 a,A,B和C 监测点的总声压级分别为 103.5,101.3 和 99.4 dB(A)。从声监测点A→B→C,总声压的降幅为2.22 dB(A)→1.93 dB(A)。对模型b,A,B和C监测点的总声压级分别为 94.3,92.1 和 90.3 dB(A)。从声监测点A→B→C,总声压的降幅为2.15 dB(A)→1.86 dB(A)。对模型c,A,B和C监测点的总声压级分别为 92.6,90.5 和 88.6 dB(A)。从声监测点A→B→C,总声压的降幅为2.06 dB(A)→1.87 dB(A)。对模型d,A,B和C监测点的总声压级分别为88.0,85.9和83.9 dB(A)。从声监测点A→B→C,总声压的降幅为2.10 dB(A)→1.92 dB(A)。因此距离绝缘子越远,总声压的降幅越小。
(3)对同一个模型,噪声在各监测点的分布规律基本相同,只是幅值不同。但对不同的模型,声压在各监测点的分布规律不同。模型 A的最大声压在630 Hz处,模型B的最大声压在400 Hz处,模型C的最大声压在250 Hz处,模型D的最大声压在200 Hz处,因此,从模型A→模型D,最大声压所处的频率是逐渐降低的,而且越来越远离人耳对声音的敏感频率点2 kHz,说明消除棱角不仅可以大幅度降低噪声,而且可以使噪声幅值远离人耳的敏感频率区。
(4)对声监测点A,B和C,模型a所对应的总声压级最高,模型b的次之,模型d的最少,说明从降低气动噪声的角度出发,将绝缘子的截面形状设计为矩形是最不利的,设计为椭圆最可取,但椭圆的长轴应跟气流流向一致,即跟列车行进方向一致,而且只含有2个椭圆形截面绝缘子所诱发的气动噪声是最低的,因此,通过加大受电弓零部件尺寸,减少受电弓零部件的数量是降低受电弓气动噪声的有效途径。
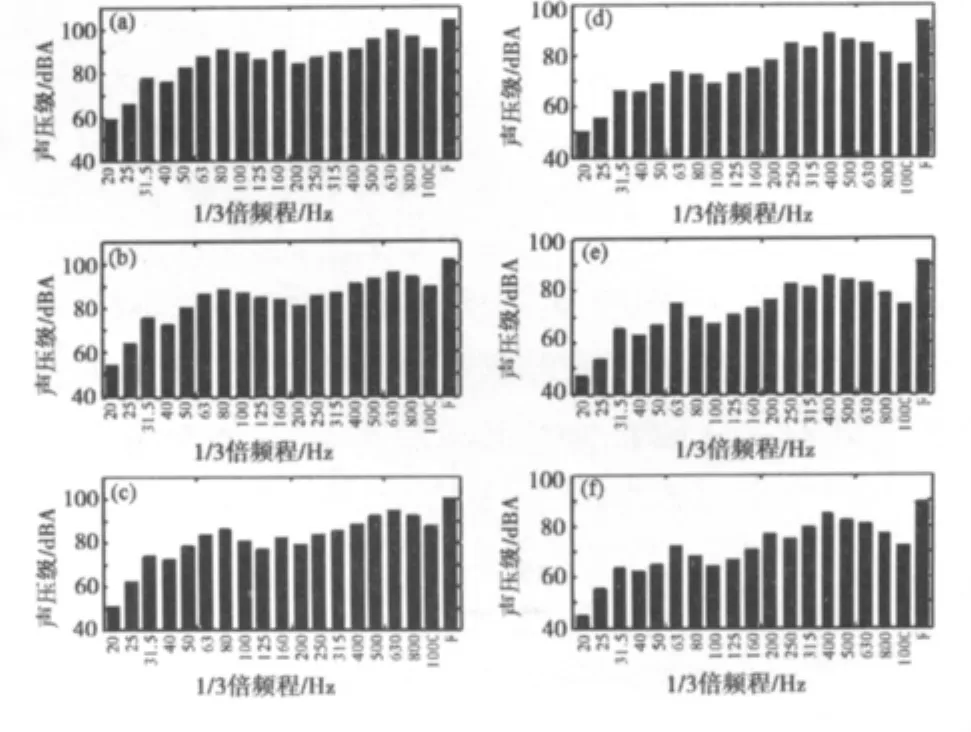
图5 模型a和b各声监测点A声级的1/3倍频程频谱Fig.5 SPL at the monitoring points in model a,b

图6 模型c和d各声监测点A声级的1/3倍频程频谱Fig.6 SPL at the monitoring points in model c,d
3 结论
(1)对同一个模型,噪声在各声监测点的分布规律基本相同,只是幅值不同。但对不同的模型,声压在各声监测点的分布规律不同。绝缘子的截面从矩形→圆形→椭圆形,最大声压所在的频率区逐渐降低,且越来越远离人耳对声音的敏感频率点2 kHz。说明消除截面的棱角不仅可以大幅度降低噪声,而且可以使噪声幅值远离人耳的敏感频率区。
(2)从降低气动噪声的角度出发,优化的绝缘子截面形状应该是椭圆形,但椭圆的长轴应跟气流流向一致。加大受电弓零部件尺寸,减少受电弓零部件的数量,是降低受电弓气动噪声的有效途径。
[1]Moritoh Y,Zenda Y.Aerodynamic noise of high-speed railway cars[J].Japanese Railway Engineering,1994,130(7):5-9.
[2]Mellet C,Letourneaux F,Poisson F,et al.High speed train noise emission:Latest investigation of the aerodynamic/rolling noise contribution[J].Journal of Sound and Vibration.2006,293(3):535-546.
[3]肖友刚,康志成.高速列车车头曲面气动噪声的数值预测[J].中南大学学报:自然科学版,2008,39(6):1267-1272.XIAO You-gang,KANG Zhi-cheng.Numerical prediction of aerodynamic noise radiated from high speed train head surface[J].Journal of Central South University:Science and Technology,2008,39(6):1267 -1272.
[4]Talotte C,Gautier P E,Thompson D J,et al.Identification,modeling and reduction potential of railway noise sources:A critical survey[J].Journal of Sound and Vibration,2003,267(2):447 -468.
[5]郑拯宇,李人宪.高速列车表面气动噪声偶极子声源分布数值分析[J].西南交通大学学报,2011,46(6):996-1002.ZHENG Zheng-yu,LI Ren-xian.Numerical analysis of aerodynamic dipole source on high-speed train surface[J].Journal of Southeast University,2011,46(6):996 -1002.
[6]朱剑月,景建辉.高速列车气动噪声的研究与控制[J].国外铁道车辆,2011,48(5):1 -8.ZHU Jian-yue,JING Jian-hui.Research and control of aerodynamic noise in high speed trains[J].Foreign Railway Car,2011,48(5):1 -8.
[7]Ikeda M,Morikawa T,Manabe K.Development of low aerodynamic noise pantograph for high speed train[C]//Proc 1994 Int Congr Noise Control Eng,1994:169 -178.
[8]Iwamoto K,Higashi A.Some consideration toward reducing aerodynamic noise on pantograph[J].Japanese Railway Engineering,1993,122(2):1 -4.
[9]孙艳军,梅元贵.国内外动车组受电弓的气动噪声介绍[J].铁道机车车辆,2008,28(5):32 -35.SUN Yan-jun,MEI Yuan-gui.Introduction of aerodynamic noise generated by foreign EMUs pantograph[J].Railway Locomotive & Car,2008,28(5):32 -35.
[10]Sueki T,Ikeda M,Takaishi T.Aerodynamic noise reduction using porous materials and their application to high-speed pantographs[J].Quarterly Report of Railway Technical Research Institute,2009,50(1):26 -31.
[11]Holmes B,Dias J.Predicting the wind noise from the pantograph cover of a train[J].International Journal for Numerical Methods in Fluids,1997,24(12):1307 -1319.
[12]Lighthill M J.On sound generated aerodynamically:Ⅰ.General theory[J].Proceedings of the Royal Society of London,1952,211A(1107):564 -587.
[13]Ffowcs Williams J E,Hawkings D L.Sound generation by turbulence and surfaces in arbitrary motion[J].Philosophical Transactions for the Royal Society of London:Series A,Mathematical and Physical Sciences,1969,264(1151):321-342.
[14]肖友刚,张晓缝,康志成.高速列车车头曲面脉动压力的大涡模拟[J].四川大学学报:工程科学版,2010,42(1):227-232.XIAO You-gang,ZHANG Xiao-feng,KANG Zhi-cheng.Large eddy simulation for fluctuation pressure of high speed train head surface[J].Journal of Sichuan University:Engineering Science Edition,2010,42(1):227 -232.
[15]马大猷.现代声学理论基础[M].北京:科学出版社,2004.MA Da-you.Modern acoustics theory[M].Beijing:Science Press,2004.

