一种新型有限元模型在接触网绞线力学特性分析中的应用*
周 伟,田红旗
(中南大学轨道交通安全教育部重点实验室,湖南 长沙 410075)
金属绞线由多股金属丝绞捻而成,其应用场合依绞线的金属材料不同而不同:钢绞线结构广泛应用于铁路桥梁、公路桥梁、房屋建筑等预应力结构;铜合金绞线在铁路电气化系统中用作接触网的重要承载部件[1],如接触悬挂结构的承力索、吊弦、弹性吊索和中心锚结绳等。金属绞线产品从设计、加工到应用,其结构的力学行为预测及精确数值模拟一直是工程领域关注的重点和难点。随着计算机技术的发展和计算机性能的不断提高,通过有限元法可实现对金属绞线力学行为的精确模拟。然而,在整体结构分析中,作为子部件若将绞线结构采用空间实体单元精细离散,数值求解规模势必会惊人,传统做法一般将绞线截面折合成单圆匀质杆件进行计算,而实际上绞线为柔性结构,其截面惯性矩要比等截面积匀质圆杆小[2],且同等载荷水平下绞线中心股线与缠绕股线的应力各不相同,因此,有必要对金属绞线的力学特性进行深化研究,以构造一种既能精确模拟绞线力学行为,又能最大程度减缩求解自由度的有限元模型。
国内外对绞线力学行为分析和数值仿真技术研究有很多报导。Jiang[3-7]等通过精确模拟相邻层绞线边界条件,提出了一种综合考虑拉伸、剪切、弯曲和扭转效应的有限元模型,分析结果与Constello[8]理论计算结果较吻合;Ghoreishi等[9]采用三维有限元法对承受静态轴向载荷的七芯绞线弹性行为进行了研究;Stanova等[10-11]提出了基于可变参数方程的任意多股绞线模型自动生成算法,通过六面体单元结构网格离散和线间面-面接触定义对模型进行了有限元分析;Usabiaga等[12]基于Love弹性细杆理论和丝间无相对滑移假设,提出了拉伸和扭转载荷作用下的新型绞线建模及分析方法;Elata等[13]充分考虑绞线各丝的双螺旋结构导致相关绞线丝应力水平对整体承载水平的影响,构造的模型可用于估计丝间相互作用力、绞线刚度和强度等参数;王应军等[14]引入形状系数的概念,从理论上对钢绞线的弹性模量表达式进行了推导,并分析了钢绞线弹性模量的影响因素。针对有限元分析特点,本文略去绞线结构的CAD建模过程,采用分段等间距截面轨迹节点扫略和滚动节点—梁单元映射直接生成绞线有限元拓扑模型,基于弹性理论和几何协调分别对拉伸和弯曲载荷作用下单股绞线结构缠绕股线节点和中心股线节点的位移约束方程进行了推演和推广,并通过具体算例对扩展模型进行验证。
1 模型建立
金属绞线从结构上可分为中心股线和螺旋缠绕股线2部分。中心股线轴线与绞线轴线重合,缠绕股线则以一定的螺旋角缠绕在其内层股线外侧,相邻层股线左右螺旋方向相反,以抵消同向缠绕给绞线带来的单向扭转。金属绞线通常以股数、股径及捻距等参数来区分,常见的绞线类型有单股1×7绞线、双股1×19绞线和3股1×37绞线。本文以单股1×7绞线作为研究对象,并将研究结论推广到多股绞线模型。
定义缠绕股线轴心螺旋轨迹线为缠绕边丝,中心股线轴心轨迹线为中心丝,同时定义中心股线上某点处的法向平面为绞线结构在该点处的法向面。考虑1个捻距的绞线结构,采用足够密集的等间距绞线法向面截取各丝,可获得中心丝和各缠绕边丝的轨迹点,将这些轨迹点定义为有限元离散节点,并在相邻截面的相应轨迹节点之间创建圆形截面梁单元,所得到的节点-梁单元模型即为绞线结构的有限元分析模型,该模型能够精确模拟绞线的几何特征,如图1所示。

图1 绞线模型的分段轨迹节点扫略和节点-梁单元映射Fig.1 Sectional path-node sweeping and node-beam mapping
记单股绞线捻距为p,中心股线直径为dc,缠绕股线直径为dh1,缠绕股数为m=6,拟合轨迹节点截面数为n。以绞线端部中心丝节点为原点建立总体笛卡尔坐标系,oz轴沿中心丝轴向,O-xy平面与端部截面相重合,如图2所示。
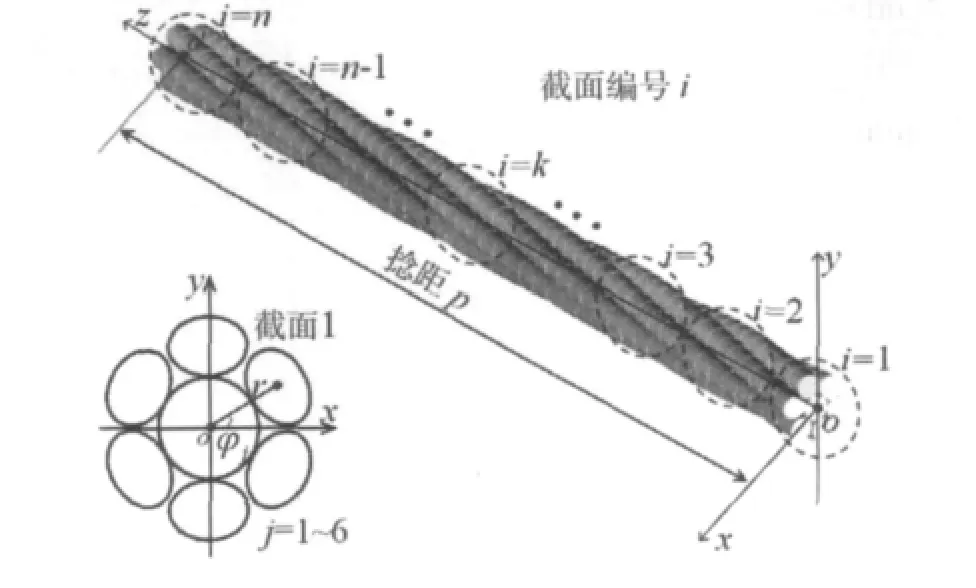
图2 1×7绞线模型几何参数Fig.2 Geometrical parameters of seven-wire strand model
初始化端部截面内各丝轨迹节点的极坐标值,中心丝节点坐标为(0,0),边丝节点坐标为 (r,φj),其中r为缠绕股线轴心圆柱半径,且r=(dc+dh1)/2。
缠绕边丝j在第k(k=1~n)个截面内的轨迹节点坐标可表示为:
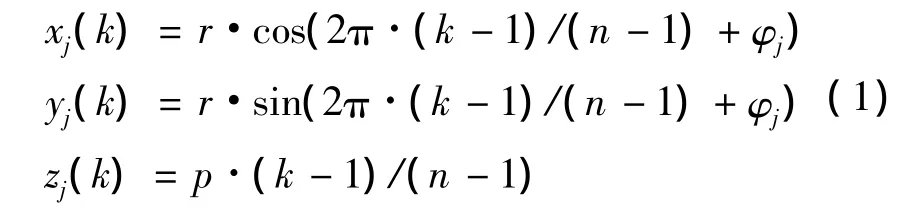
由于缠绕边丝节点与中心丝节点无几何约束,受力状态下必定会呈现两者变形的不相关,因此,必须建立不同受力状态下缠绕边丝与中心丝轨迹节点的几何约束方程,以准确描述绞线结构的力学特性及几何协调性。子约束方程的施加对象为缠绕边丝节点、同截面及相邻截面中心丝节点,为保证节点、单元及相应节点约束方程的一一对应,有限元模型必须采取滚动映射的方式生成,流程如下。
(1)参数初始化。捻距p、中心股线直径dc、缠绕股线直径dh1、拟合截面数n等。
(2)端部截面定义。端部截面轨迹节点坐标初始化并创建该节点及其子约束方程。
(3)遍历截面i=2~n,同时建立该截面中心丝轨迹节点,并定义该节点与第(i-1)截面对应节点之间的梁单元。
(4)遍历各缠绕边丝j=1~6。计算截面i内缠绕边丝轨迹节点坐标(xj(k),yj(k),zj(k))并创建相应节点及其子约束方程,定义该节点与第(i-1)截面对应节点之间的梁单元。
(5)截面遍历是否结束,否则,转到第(3)步。
对多股绞线结构,式(1)中第i层缠绕股线的参数r取该股线轴心圆柱半径,并对其轨迹节点x、y坐标的角度变量取反即可保证相邻层股线螺旋方向相反。
绞线结构有限元分析模型建立的难点是相邻层股线之间几何约束方程的准确描述,下面将对此展开论述。
2 约束条件
绞线股间几何约束方程的推导基于以下假设:绞线整体承受轴向拉伸载荷时,绞线相对其轴线不发生相对扭转,摩擦条件下股线之间无自由滑移;绞线整体承受纯弯曲载荷时,同一截面缠绕边丝节点与中间丝节点相对位置保持不变,摩擦条件下股线间无自由滑移,股间绞线变形满足位移协调。
下面将分别对轴向和弯曲变形情况下单股绞线股间几何约束方程进行推导,并将结论直接推广至多股绞线结构。
2.1 轴向变形股间几何约束方程
在同等轴向拉伸载荷作用下,绞线各股将互不干扰地沿其轴线方向伸长。由于材料的泊松效应,中心股线和缠绕股线的分布圆柱直径以及绞线总体直径均会发生变化,且两者的轴向应变满足线性关系。
假定各股线材料泊松比v均相同,中心股线轴向应变为εc,缠绕股线轴向应变为εh1,几何参数定义与前文同。根据泊松比定义,绞线受力后中心股线和缠绕股线的直径分别变为(1-vεc)·dc和(1-vεh1)·dh1,缠绕股线变形前后的长度分别为:
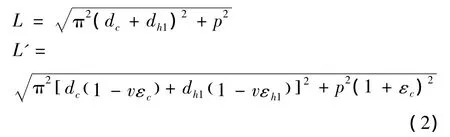
缠绕股线的轴向应变可表示为:
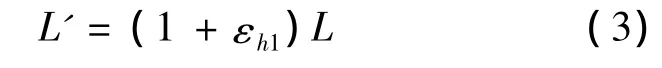
由式(2)和(3)得:

其中:两者的应变比系数kh1为:
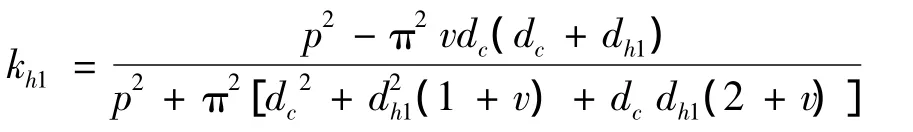
以绞线端部截面中心点为原点建立总体笛卡尔坐标系,oz轴沿中心股线轴向,O-xy平面与端部截面重合,同时在该坐标系原点处建立极坐标系,两坐标系坐标轴重合。节选1个捻距的中心股线和单根缠绕股线,取缠绕边丝某节点 P(rP,θP,zP)、同截面中心丝节点Ok(0,0,zP)及相邻截面中心丝节点 Ok-1(0,0,zk-1)为分析对象,如图 3 所示。
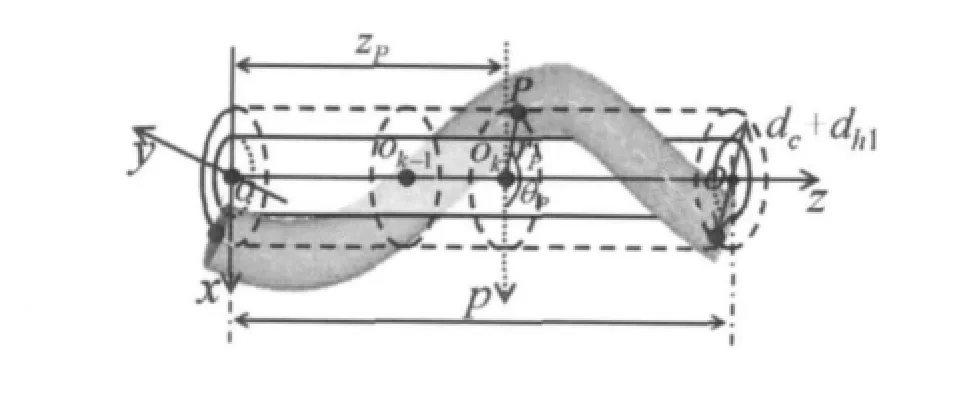
图3 拉伸变形下坐标系定义及分析对象选取Fig.3 Coordinate system and analytical targets in axial tension
根据假设,对象节点的极坐标位移向量分别记为 P(ΔrP,ΔθP,ΔzP),Ok(0,0,Δzk) 和 Ok-1(0,0,Δzk-1),则节点 P 的极点位移为:
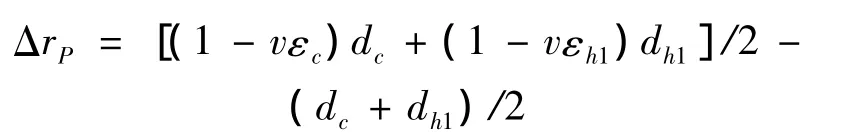
中心股线轴向应变可表示为:
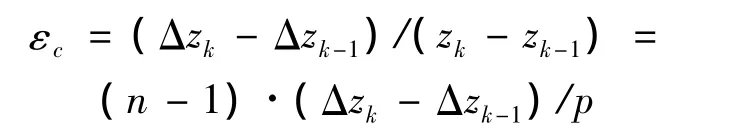
结合式(4),节点P的极坐标位移可表示为:
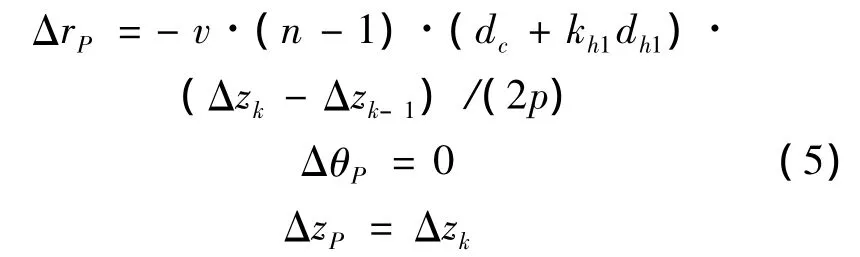
通过坐标转换,节点P的总体位移向量为:
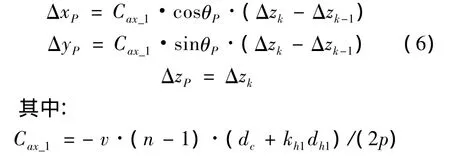
式(6)即为轴向变形下单股绞线股间几何约束方程。对多股绞线结构,记第i层缠绕股线直径为dhi,捻距为pi,该层缠绕股线与中心股线的应变比系数记为khi,该层缠绕股线轴心圆柱直径记为:
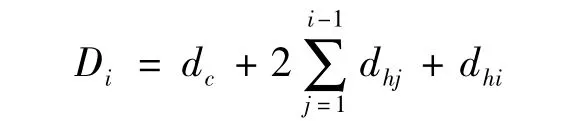
修正应变比系数khi,得:
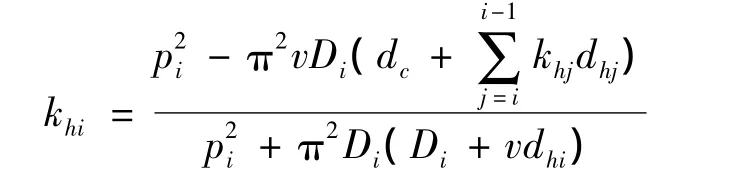
第i层缠绕股边丝节点、同截面与相邻截面中心丝节点的位移约束方程与式(6)形式相同,仅需对系数Cax修正如下:
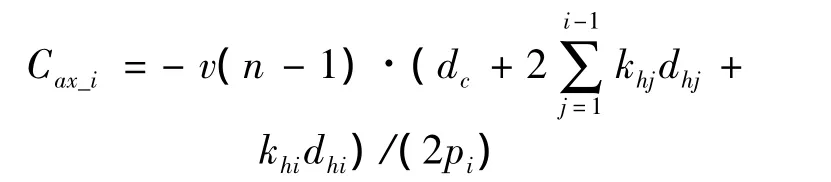
2.2 弯曲变形股间几何约束方程
在绞线纯弯曲状态下,中心股线的变形满足初等力学平面截面假设,缠绕股线的变形必须与中心股线相协调,单股绞线股间几何约束关系也是基于这一原则进行推导。
选取绞线端部截面中心点建立总体笛卡尔坐标系,坐标轴方向定义与前面的相同。取缠绕边丝某节点P、同截面及相邻截面中心丝节点I和J为分析对象,在绕x轴弯矩Mx作用下,各节点位置分别记为P'、I'及J',绞线弯曲曲率中心记为Ol,曲率半径记为ρ,如图4所示。
根据假设及几何协调条件,纯弯曲下节点P'、I'与曲率中心点ol在同一直线上,且节点P'与I'相对位置保持不变。
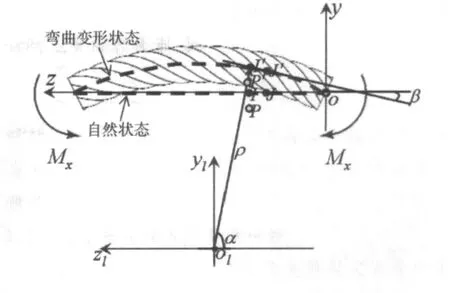
图4 纯弯曲状态下绞线的几何协调Fig.4 Geometrical compatibility of wire strand under bending
以曲率中心ol为原点建立局部坐标系ol-ylzl,olP'与olzl轴夹角记为α,节点I'、J'所在直线与oz轴夹角记为β,拟合截面数n足够大的情况下可以认为节点I'和J'所在直线为弯曲弧在点I'处的切线,因此,有 α +β =90°。
记节点P的总体坐标为(xP,yP,zP),则节点I',P'的局部坐标分别为:
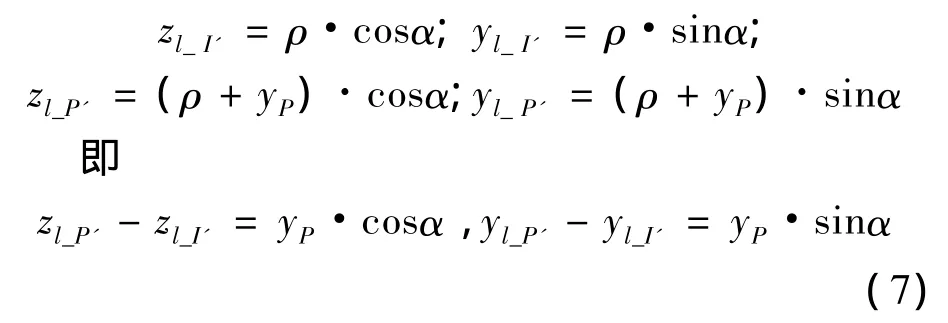
在自然状态下,有:
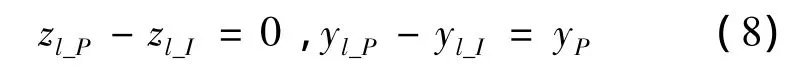
由于总体坐标系与局部坐标系平行,对象节点的局部位移关系可直接转换到总体坐标系,由式(7)~(8)得:
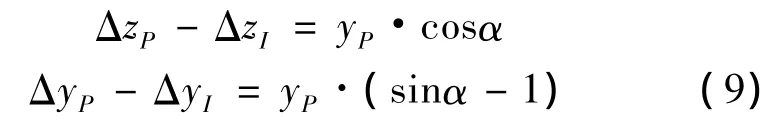
另一方面,点I'处切线与oz轴夹角β满足
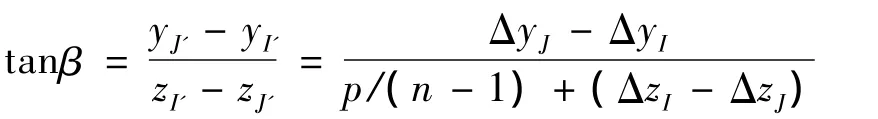
事实上,相邻截面中心丝节点的位移差要远小于相邻截面距离,即ΔzI≪ΔzJ<< p/(n–1),加之绞线小位移变形情况下β为极小角,故有:
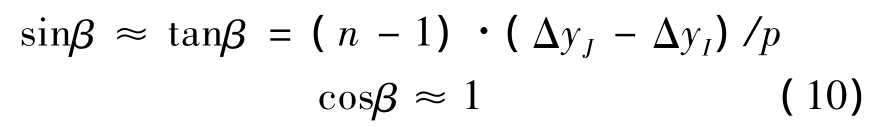
结合式(9)和(10),并考虑节点P在x方向的位移,可得纯弯曲变形下单股绞线股间几何约束方程为:
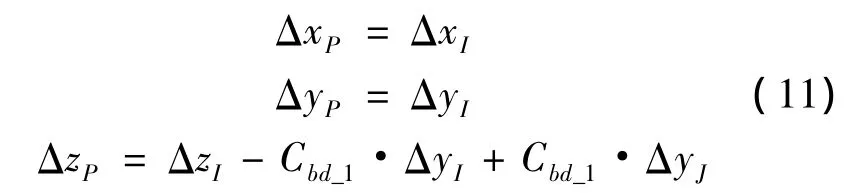
其中:
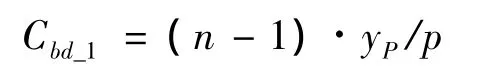
若弯矩载荷绕y轴方向,则约束方程仅需调换式(11)中变量’x’和’y’即可。对多股绞线结构,记第i层缠绕股线捻距为pi,拟合截面数为ni,该层缠绕股线节点位移约束方程与(11)形式相同,仅需对系数Cbd修正如下:
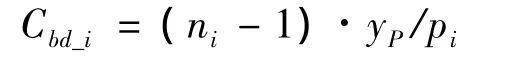
3 算例分析
本文的模型算法及求解分析均在大型有限元分析软件ANSYS11.0中进行。由于绞线模型采用分段截面梁单元模拟,足够拟合精度下相邻截面之间的梁单元均具有大径跨比,因此,单元类型选择基于经典Timoshenko梁理论的Beam188单元,该单元综合考虑了剪切变形和转动惯量,并对挠度与截面转角各自独立插值[15]。
将模型各节点子约束方程进行组集,可得到整体模型的多自由度系统约束方程Au=b。为施加约束条件,引入拉格朗日乘子λ构造变分,形成泛函:
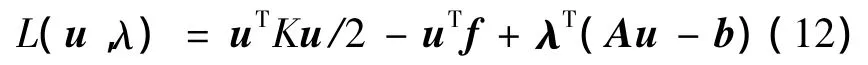
其中:K为结构总体刚度矩阵;f为总体载荷列阵。
泛函L(u,λ)分别对函数u和λ取极值,得到系统求解方程的矩阵形式为:
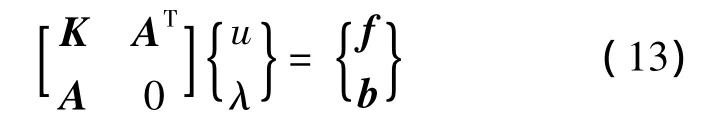
通过求解方程(13),即可得到不同载荷工况下各节点位移。
为验证本文方法,模型的选取参照文献[8],轴向拉伸工况分析对象为双股1×19绞线,水平弯曲工况分析对象为单股1×7绞线,分析对象的材料及几何参数与文献[8]的相同,如表1所示。

表1 不同工况绞线材料及几何参数定义Table 1 Material and geometry parameters definition
双股1×19绞线内外层缠绕股以相反螺旋缠绕,两层缠绕股线捻距相同,采用分段截面轨迹节点扫略和滚动单元映射,创建一个捻距长度的双股绞线三维有限元模型如图5所示。
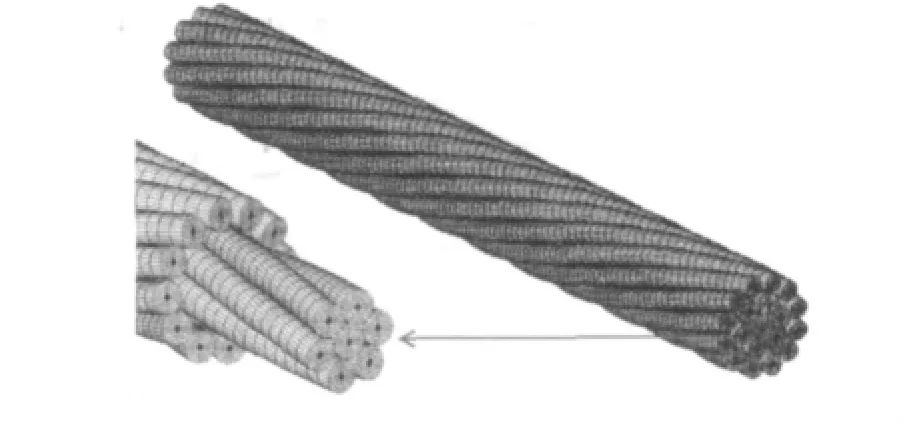
图5 单捻距长度双股绞线有限元模型Fig.5 Finite element model of 1 × 19 strand of a pitch length
轴向拉伸计算工况下,对双股绞线端部截面节点施加全约束,并在他端中心节点处施加轴向拉伸力T;水平弯曲计算工况下,对单股绞线两端中心节点施加垂向约束,并在绞线中部截面中心丝节点处施加垂向集中力。端部轴向拉伸力T从50~400 kN变化,双股绞线的轴向伸长量变化如图6(a)所示;中部垂向集中力Fy从100~1000 N变化,中部垂向挠度变化如图6(b)所示。

图6 分析结果与Costello理论计算值的比较Fig.6 Analytical results comparison;the suggested FEA model,theory of Costello
端部轴向拉伸力T=400 kN时,双股绞线的轴向伸长量为1.3728 mm,Costello理论计算值为1.3969mm,两者相对误差为1.72%;中部垂向集中力Fy=1000 N时,单股绞线中部垂向挠度为6.326 mm,Costello理论计算值为 6.745 mm,两者相对误差为6.21%。不同计算工况下两者的变形情况如图7所示。
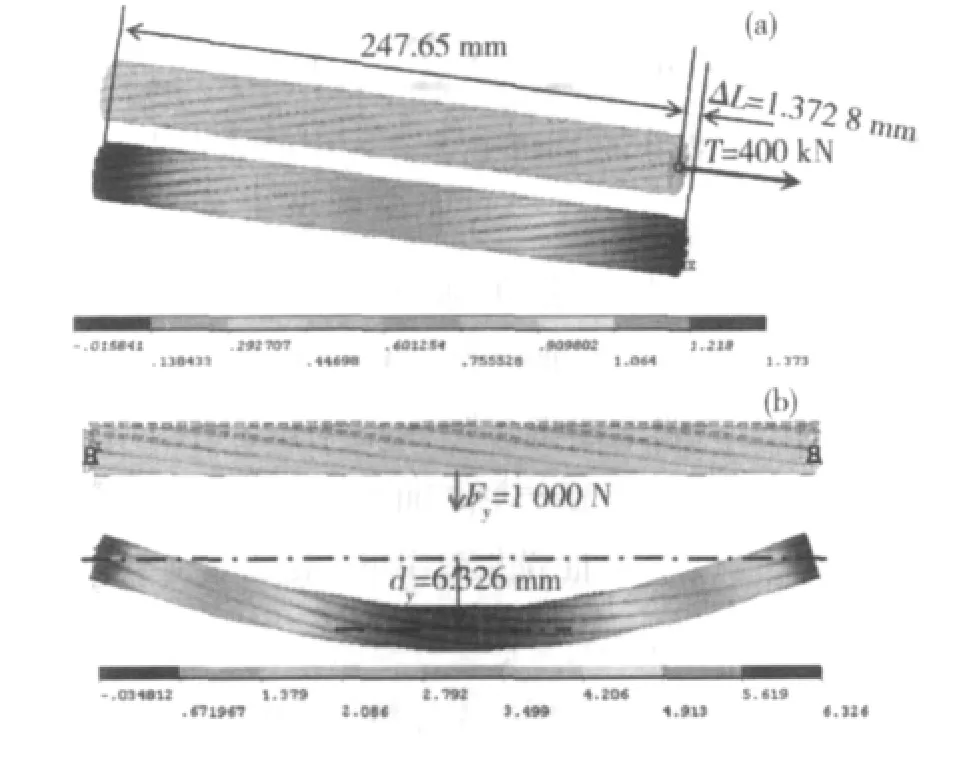
图7 端部轴向拉伸和水平弯曲计算工况下绞线变形图Fig.7 Deformation map of wire strand in axial tension and pure bending
4 结论
(1)采用分段截面轨迹节点扫略和滚动梁单元映射构造了多股绞线有限元分析模型的自动生成算法。
(2)基于材料弹性理论和几何协调创建了轴向拉伸和水平弯曲变形情况下单股绞线的股间几何约束方程,并推广到了多股绞线结构。
(3)基于Timoshenko梁理论和Lagrange乘子法对单捻距双股和单股绞线结构进行了多工况有限元分析,并与Costello理论值进行了比较,横向拉伸和水平弯曲变形下两者相对误差分别为1.72%和6.21%。结果表明,该有限元分析模型能够精确模拟多股绞线的力学特性,为接触网承力索等金属绞线结构的力学分析提供了一种简单有效的理论模型和方法。
(4)纯弯曲情况下绞线股间几何约束方程基于小变形假设而创建,因此有必要在下一步工作中对大位移变形下的绞线股间几何协调机制进行深入研究。
[1]王作祥.电气化铁道接触网用绞线标准的技术内涵[J].铁道技术监督,2005(9):10-12.WANG Zuo-xiang.Technical connotation of catenary wire standard in railway catenary system[J].Railway Quality Control,2005(9):10 -12.
[2]孔庆凯,万 鹏.钢绞线的基本力学性能及其有限元方法模拟[J].四川建筑,2003,23(1):20-22.KONG Qing-kai,WAN Peng.Fundamental mechanicalbehavior of steel wire strand and its finite element simulation method[J].Sichuan Architectural,2003,23(1):20-22.
[3]Jiang W G,Yao M S,Walton J M.A concise finite element model for simple wire rope strand[J].International Journal of Mechanical Sciences,1999,41(2):143 -161.
[4]Jiang W G,,Henshall J L,Walton J M.A concise finite element model for 3-layered straight wire rope strand[J].International Journal of Mechanical Sciences,2000,42(1):63-86.
[5]Jiang W G,Henshall J L.The analysis of termination effects in wire strand using the finite element method[J].Journal of Strain Analysis for Engineering Design,1999,34(1):31-38.
[6]Jiang W G,Warby M K,Henshall J L.Statically indeterminate contacts in axially loaded wire strand[J].European Journal of Mechanics A/Solids,2008,27(1):69 -78.
[7]Jiang W G.A concise finite element model for pure bending analysis of simple wire strand[J].International Journal of Mechanical Sciences,2012,54:69 -73.
[8]Costello G A.Theory of wire rope.2nd ed[M].New York:Springer- Verlag,1997.
[9]Ghoreishi S R,Messager T,Cartraud P,Davies P.Validity and limitations of linear analytical models for steel wire strands under axial loading,using a 3D FE model[J].International Journal of Mechanical Sciences,2007,49(11):1251-1261.
[10]Stanova E,Fedorko G,Fabian M,Kmet S.Computer modelling of wire strands and ropes Part I:Theory and computer implementation[J].Advances in Engineering Software,2011(42):322-331.
[11]Stanova E,Fedorko G,Fabian M,Kmet S.Computer modelling of wire strands and ropes part II:Finite element-based applications[J].Advances in Engineering Software,2011(42):305 -315.
[12]Usabiaga H,Pagalday J M.Analytical procedure for modelling recursively and wire by wire stranded ropes subjected to traction and torsion loads[J].International Journal of Solids and Structures,2008,45(21):5503-5520.
[13]Elata D,Eshkenazy R,Weiss M P.The mechanical behavior of a wire rope with an independent wire rope core[J].International Journal of Solids and Structures,2004,41(5):1157-1172.
[14]王应军,李卓球,宋显辉.钢绞线弹性模量的理论计算及其影响因素分析[J].武汉理工大学学报,2004,26(4):80-82.WANG Ying-jun,LI Zhuo-qiu,SONG Xian-hui.Theoretical computing&analysis affecting factors on stranded wire's elastic module[J].Journal of Wuhan University of Technology,2004,26(4):80 -82.
[15]高兴军,马海涛,陈太聪.弹性地基上Timoshenko梁的精确数值解[J].计算力学学报,2011,28(6):904-908.GAO Xing-jun,MA Hai-tao,CHEN Tai-cong.Exact numerical solutions of timoshenko beams on elastic foundations[J].Chinese Journal of Computational Mechanics,2011,28(6):904 -908.

