中薄板坯结晶器内钢液流动数值模拟
高爱民,张燕,张彩军
(河北联合大学冶金与能源学院,河北唐山063009)
中薄板坯结晶器内流场的基本形态是射流由水口出口冲向结晶器窄壁,由于射流的卷吸和剪切作用,结晶器内钢液形成向上和向下两个回流区。上升流股对夹杂物上浮、弯月面波动产生影响,决定钢渣卷混状况,同时也为保护渣的熔化提供热量,决定渣层的厚度;下降流股对结晶器下端,甚至二冷段的结晶组织产生影响。充足的向上流动能防止弯月面凝固、有利于夹杂物的上浮,但过强会导致液面波动和卷渣,而过强的向下流动不利于夹杂物和气泡上浮。因此系统研究结晶器内流场的影响因素尤为重要。本文以某钢铁公司的中薄板坯连铸结晶器为例,利用FLUENT商业软件对中薄板坯连铸过程中结晶器内流体流动和热量传输进行数值模拟,研究拉速和浸入深度对结晶器内流场的影响规律,为实际生产提供理论分析。
1 模型建立和求解
1.1 基本假设
实际结晶器内钢液受到凝固、振动等多方面因素的影响,其流动是十分复杂的过程。但在数值模拟过程中为了提高计算效率,对所研究的问题需进行合理的简化和必要的假设。本文的假设主要有以下几点:
(1)结晶器内钢液流动为粘性不可压缩流动;
(2)结晶器内钢液按均相介质处理;
(3)不考虑结晶器振动等因素对流场的影响;
(4)忽略凝固对结晶器的影响。
1.2 基本方程
数值模拟以描述结晶器内钢液流动的三维稳态不可压缩问题的数学模型为基础,反映钢液粘性流动的主导方程主要有连续方程、动量方程、湍动能方程和湍动能耗散率方程。
连续性方程:

动量方程(N-S方程):

湍动能k方程:

湍动能耗散率方程ε:

式中,ρ为钢液密度,kg·m-3;ui、uj为湍流流动的时均速度,m·s-1;P为作用在流体微元体上的压力,Pa;μeff为有效粘度系数,Pa·s;k为湍动能,m2·s-2;ε 为湍动能耗散率,m2·s-3;σk,σε为湍动能k和耗散率ε对应的Prandt数;keff为有效传热系数,W·m-1·K-1;μ为钢液粘度,Pa·s;μt为湍流动量扩散系数或湍流粘度系数;有效粘度
k-ε双方程模型中五常数采用Launder和Spalding的推荐值,如表1所示。

表1 k-ε双方程模型中五个常数
1.3 边界条件
(1)在自由表面上,液体直接与气体接触,不与固体表面接触,表面切应力很小,可以忽略不计。对于平行于自由表面的速度分量和其它标量(如k、ε)的梯度可设为零,垂直于自由表面的速度分量设为零;
(2)在固体表面上,对速度、压力使用无滑移边界条件;
(3)入口的速度垂直于所在的面,视为稳定的一维流动。入口速度Vinlet由入口的流量和入口的面积算出;
(4)出口采用自由出流的条件,各变量的法向梯度为0;
(5)考虑到结晶器及水口形状的对称性,本模型计算实际模型的四分之一,取结晶器中心相互垂直的结晶器宽边和窄面为对称面。在对称面处各变量法向方向量设为零;
(6)在与壁面相邻的粘性层中,湍流的雷诺数Re很低,这时必须要考虑分子粘性的影响,因此,湍流发展并不充分,流动可能处于层流状态,所以应该对所用的湍流模型必须加以修正。对于k-ε双方程模型来讲,此时系数Cμ将与湍流雷诺数Re有关,采用标准壁面函数法。
1.4 求解方法
模型建立以后,要进行数值求解必须进行方程的离散,然后对离散方程迭代求解。具体步骤如下:
(1)研究对象几何模型的建立,确定计算区域;
(2)数字化几何模型的离散,即划分网格;
(3)对所建立数学模型,进行方程离散;
(4)在划分网的基础上,对离散化后方程进行迭代求解。其中需要确定迭代步数、迭代收敛标准等;(5)对求解所得结果进行处理,以获取所需的定性图片和定量数据。
2 分析讨论
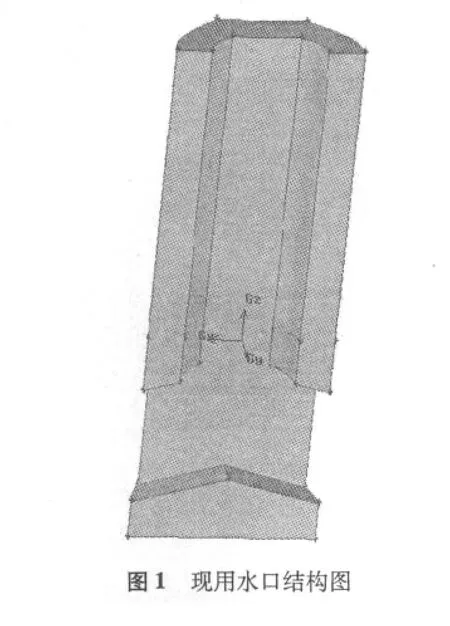
建立的数学模型对象为三维的中薄板坯结晶器,依据某钢铁公司连铸车间生产的实际情况对浸入式水口和结晶器三维流场进行计算。该钢铁公司连铸车间使用的实际水口为扁平结构。将浸入式水口与钢液面水平的截面中心点定义为坐标原点,水口宽面方向为X轴,窄面方向为y轴方向,长度方向为z轴,取结晶器的1/4为计算域,水口结构与计算域网格的划分如图1和图2所示。
2.1 拉速对结晶器内钢液流动的影响

当浸入深度一定时,拉速分别为1.1m/min、1.3m/min和1.5m/min,分析不同拉速下的自由液面流速和表面湍动能,研究拉速对结晶器流场的影响。
图3和图4分别给出了不同拉速下自由液面附近表面流速和液面湍动能分布图。由图3可见,随着拉速增加,自由液面流速有所增加,而且不同拉速时流体的流动状态很相似。虽然拉速对结晶器内流动规律的影响不是主要的,但从液面稳定来看,其影响不可低估。随着拉速的增大,结晶器内钢液表面流速随之增大,冲击深度变深,造成夹杂物的穿透深度随之增加,不利于夹杂物的上浮,同时钢液面变得更加不稳定,容易造成保护渣的卷入和钢液面裸露,使钢液中夹杂物增加,降低了铸坯质量。


由图4可以看出,湍动能随拉速的提高而增加,湍动能最大值出现在靠近窄面一侧。拉速由1.1m/min提高到1.3m/min时,湍动能的增加较平缓;当拉速提高到1.5m/min时,湍动能发生了剧烈的改变。
2.2 水口浸入深度对结晶器内钢液流场的影响
固定拉坯速度,插入深度分别为110mm、130mm、150mm和170mm,分析不同浸入深度下的钢液冲击深度、表面流速及表面湍动能,研究浸入深度对结晶器流场的影响。图5给出了不同水口浸入深度下,结晶器内钢液流场分布。

由图5可以看出,随浸入式水口浸入深度的增加,流场的冲击深度、涡流中心的高度都随之增大,这大大减少由中间包进入结晶器夹杂物的上升机会以及气泡的上浮,同时会造成结晶器内高温区下降,不利于保护渣的熔化。结果引起结晶器润滑不良、铸坯与结晶器的摩擦阻力增大,可能造成粘结而拉漏,也可使连铸坯内部缺陷增多。但是,较大的浸入深度会使结晶器内钢液向上运动的回流范围变大,结晶器自由表面处液面波动幅度明显减小,这样有利于减少保护渣卷入的机会,防止产生新的夹杂物。
图6给出了不同浸入深度下自由液面附近表面流速,当插入深度为110mm、130mm、150mm时,表面流速变化不明显。当插入深度为170mm时,液面过于平静,向下回流的涡心位置在下移,这对夹杂物与气泡上浮不利。
由于随着插入深度的增加,向上流股充分发展,结晶器液面的回流速度减弱,扰动也随之减弱。图7给出了不同水口插入深度下自由液面湍动能分布曲线。由图7可以看出,插入深度的增加对靠近窄面附近的湍动能分布影响不大。插入深度为150mm时,水口附近的湍动能最大,此时易造成卷渣。当浸入深度增加至170mm时,由于上部流场得到发展,液面出现局部不稳定的现象,同时,插入深度170mm的湍动能的峰值出现在相对靠近窄面的位置。


3 结论
随着拉速的提高,尽管有利于保护渣的熔化,但熔池表面变得更加不稳定,易造成保护渣的卷入和钢液面裸露,使钢中夹杂物增加,降低铸坯质量;随着拉速提高,结晶器内高温区下移,容易使连铸操作增加漏钢
和鼓肚等事故的隐患。对于浸入深度来说,较大的插入深度会使熔池表面向上运动的回流范围变大,结晶器自由表面处液面波动幅度明显减小,这样有利于减少保护渣卷入的机会,防止产生新的夹杂物;但浸入深度过深,弯月面处钢液湍动能过小,液面不活跃,不利于保护渣熔化。插入深度过浅时,钢液面湍动能过大,易产生卷渣和钢液裸露现象。因此,拉速和浸入深度对结晶器内钢液流动的影响很大,实际生产中兼顾拉速和浸入深度,使熔池中流场和湍动能分布更加合理。
[1] 张兴中,我国连铸技术的发展状况和趋势[J].钢铁研究学报,2004,16(6):1-6.
[2] 中国金属学会连铸专业委员会.我过连铸技术的现状与展望[J].中国冶金,2000,(5):26-33.
[3] J.Birat,M.Larrecq,J.Lamant and J.Petegnief,The Continuous Casting Mold:A Basic Tool for Surface Quality and Strand Productivity[C],Mold Operation for Quality and P roductivity,1991,3-14.
[4] W.HEmling,T.AWaugaman.Subsurface Mold Slag Entrainment in Ultra Low Carbon Steels[J].Steelmaking Conference Proceedings,1994:371-374.
[5] 万晓光.板坯连铸结晶器内钢液流动行为的研究[D],北京:北京科技大学,2000.
[6] 幸伟,沈巧珍.方坯连铸结晶器浸入式水口结构类型的研究[J].钢铁研究,2004,(5):24-27.
[7] 幸伟,沈巧珍,王晓红.方坯连铸结晶器内钢液三维流场的数值模拟[J].山东冶金,2004,26(5):42-44.
[8] 武文斐,郑坤灿,李义科.数值模拟研究钢液入口速度对结晶器流场的影响[J].铸造技术,2003,24(2):143-145.
[9] 王仁贵,郑敏,张炯明.方坯连铸结晶器三维流场的数值模拟[J].鞍钢技术,1999,(7):4-7.
[10] 张乔英,王书桓,王立涛,等.浸入式水口底部结构对板坯结晶器内钢液流场和温度场的影响[J].钢铁研究,2005,(1):17-20.

