粘滞阻尼器在金水沟特大桥中的应用研究
周友权
(中铁第一勘察设计院集团有限公司桥隧处,西安 710043)
1 工程概况
黄韩侯铁路是连接陕西省黄陵县与山西省侯马市的1条客货共线铁路,位于铁路线上的金水沟特大桥,其主桥孔跨布置为(80+3×140+80)m,联长581.8 m,主桥3、4号主墩为刚构墩,2、5号次主墩及1、6号边墩为连续梁墩,整体结构为刚构连续梁桥。桥面与地面的最大高程差约93 m,3、4号墩墩高均为80 m,2、5号墩高均为55 m,立面布置如图1所示。桥址处的地震动峰值加速度值为0.152g,相当于地震基本烈度7度,地震动反应谱特征周期为0.43 s。由于金水沟主桥墩高联长,属于技术复杂、修复困难的特殊结构桥梁[1],并且地震动峰值加速度为0.152g,需对全桥进行专门的抗震分析,并采取一定的减震措施。

图1 全桥立面布置(单位:m)
2 主桥抗震分析
2.1 模型建立
采用Midas/Civil 2010程序,将金水沟主桥离散为空间梁单元,用M法计算桩基对承台的弹性支承刚度,在模型承台底加上6个自由度的弹性支承,计算模型如图2所示。
2.2 地震波来源

图2 计算模型
由于金水沟主桥结构的特殊性,对其桥址区做了专门的地震安全性评价工作。采用拟合基岩反应谱的三角级数迭加法合成场地基岩地震动时程,给出了50年超越概率63%、10%和2%三种设防概率水平的合成场地基岩地震动加速度时程,每种概率水平各给出了3条加速度时程。由于本桥墩高联长,属于修复困难的重点桥渡,并且桥址属于0.15g的7度区,因此拟采用3条超越概率2%的人工合成波来进行全桥的地震反应分析。当采用3条时程波计算时,时程分析的最终结果应取3组计算结果的最大值[2]。图3仅示出了50年超越概率为2%的1条时程曲线。
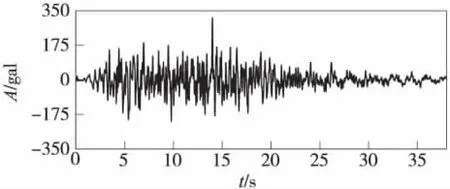
图3 水平地震动时程曲线(2%)
2.3 地震反应结果分析
将50年超越概率为2%的3条时程曲线分别输入,在Midas中采用直接积分法,得到顺桥及横桥向主桥的地震反应。当采用3条时程波计算时,时程分析的最终结果应取3组计算结果的最大值[2]。将地震力与主力进行组合,按照桥墩与桩基的实际配筋,对桩基的承载力及桥墩桩基的强度进行检算。横桥向桩基的承载力及桥墩桩基的强度均满足要求,这是由于横桥向由上部结构产生的地震力由2~5号4个主墩分担。在顺桥向,3号与4号主墩桩基承载力及桥墩桩基的强度远远超限,而其他桥墩桩基的承载力及强度还有很大的富裕量,这是由于纵桥向由上部结构产生的地震力仅由3号与4号刚构墩来承担,其余墩主要承担桥墩自身产生的地震力。另外,查看结构的地震反应发现,地震下连续梁墩墩顶处的梁与墩之间的相对位移很大,最大双边位移之和即位移幅值在40 cm左右,地震下梁端伸缩缝与边墩顶帽高出部分很容易发生破坏。因此,拟在次主墩纵向设置耗能的液体粘滞阻尼器,减小桥梁纵向的地震反应,并使次主墩分担纵向地震力的比重加大,以确保结构的安全。
3 粘滞阻尼器参数的选取
3.1 粘滞阻尼器的特性
粘滞阻尼器一般由活塞、油缸及节流孔组成,是利用活塞前后压力差使油流过节流孔产生阻尼力的一种减震装置[3]。粘滞阻尼器的公式为[4]

式中,F为阻尼力;C为阻尼器的阻尼系数;V为阻尼器两端间的相对运动速度;α为速度的指数,其取值范围为0.1~2,从抗震角度,其常用的取值范围为0.2~0.5。
由粘滞阻尼器的公式可知,在温度、收缩和徐变等荷载作用下,V值很小,粘滞阻尼器产生的阻尼力很小,对结构产生的附加力也很小[5];在地震作用下,墩梁间的相对速度很大,阻尼器可以对结构提供较大的反力,并且阻尼器自身会消耗地震产生的能量,这对于结构抗震是有利的。而且内置液体,本身没有可计算的刚度,不影响整个结构的固有周期[6]。呈椭圆形的滞回曲线,保证了安置在结构上的阻尼器在最大位移的状态下受力为零,最大受力情况下位移为零,这一性能对减小结构反应十分有利[7]。
3.2 阻尼器设置位置
地震中,梁与墩之间的位移越大,墩梁之间的相对速度才可能越大,而由式(1)可知,墩梁之间的相对速度越大,阻尼器输出的阻尼力也就越大,阻尼器对结构的地震反应抑制作用也越大。因此,阻尼器应该安置在结构最大相对位移处。对于本桥,连续梁墩墩顶的相对位移均较大,而1、6号墩为边墩,墩身及基础均较小,2、5号墩为次主墩,墩身及基础与刚构主墩相差不大。设置阻尼器后,桥墩受力会增大,考虑到桥墩及基础的设置,决定只在次主墩每个墩顶设置4个阻尼器。
3.3 粘滞阻尼器参数的对比分析
最大阻尼力和最大冲程是确定阻尼器的主要指标,而阻尼系数和速度指数是阻尼器控制作用大小的2个关键参数[8]。目前对于非线性粘滞阻尼器的设计,最终目的是确定粘滞阻尼器的阻尼系数及速度指数。通过改变阻尼系数及速度指数,可以改善并提高控制效果,但同时也可能会增加阻尼器的最大输出阻尼力,而最大阻尼力越大,阻尼器越昂贵[9]。因此,对于阻尼器的设计,实际上是一个结构设计、阻尼器参数设计、经济效益综合分析及减振预期控制目标的综合设计过程。
粘滞阻尼器参数选取的不同,其对结构响应的影响也不同。因此,需对结构引入粘滞阻尼器的情况进行结构响应分析。式(1)中,V是与结构自身有关的参数,阻尼器参数的选取,主要考虑对阻尼器参数C、α进行参数敏感性分析,研究这些参数变化对结构响应的变化规律,为粘滞阻尼器设计参数的确定提供依据[10]。表1给出了金水沟特大桥阻尼器参数敏感性分析工况。
利用阻尼器减震,主要是控制结构的最大位移和结构关键点的内力水平,桥墩的配筋及基础的承载力与墩底弯矩的大小密切相关,另外阻尼器输出的最大阻尼力是影响减震措施造价的关键参数,一般来说,最大阻尼力越大,阻尼器越昂贵。综上所述,图4~图9仅给出了不同阻尼器参数下,梁端墩梁相对位移、主墩墩底弯矩及阻尼器最大阻尼力的变化情况。地震时程中,结构的上述参数都是随时间变化的,下图仅给出了各参数地震反应中的最大值。
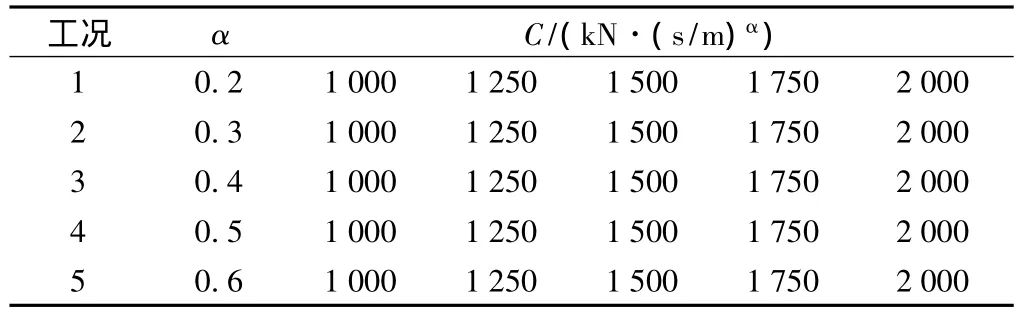
表1 金水沟特大桥阻尼器参数分析工况

图4 阻尼器参数C对主墩墩底最大弯矩的影响
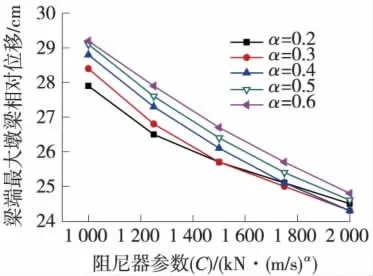
图5 阻尼器参数C对梁端最大相对位移的影响
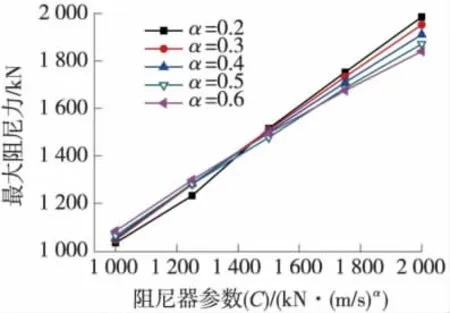
图6 阻尼器参数C对阻尼器最大阻尼力的影响

图7 阻尼器参数α对主墩墩底最大弯矩的影响
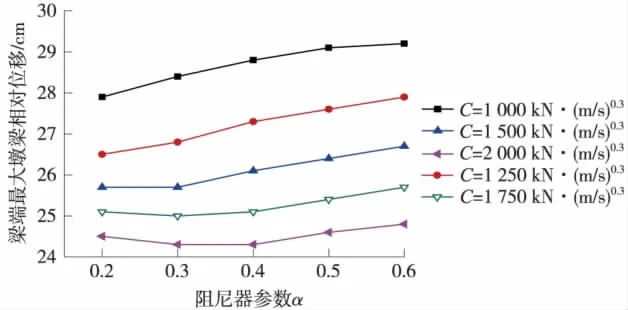
图8 阻尼器参数α对梁端最大相对位移的影响

图9 阻尼器参数α对阻尼器最大阻尼力的影响
由图4可知,随着阻尼器参数C的增大,墩底最大弯矩呈先单调递减、后单调递增趋势,即参数C有最优化值。相同的C值下,α值不同,墩底最大弯矩也不尽相同,即对于墩底弯矩来说,C与α具有相关性。由曲线图可知,当C值为1 500 kN·(s/m)0.3、α值为0.3时,墩底最大弯矩有极小值,此时的C与α值即为墩底弯矩的最优化参数。由图5与图6可知,阻尼器参数C越大,梁端最大相对位移越小,即对结构地震下的反应抑制效果越好,但是阻尼器的最大阻尼力也越大,所需阻尼器也就越昂贵。
由图7可知,随着阻尼器参数α的增大,墩底最大弯矩呈先单调递减、后单调递增趋势,即参数α也有最优化值。由曲线图可知,当 C值为1 500 kN·(s/m)0.3、α值为0.3时,墩底最大弯矩有极小值,此时的C与α值即为墩底弯矩的最优化参数。图7与图8的曲线接近于直线,即阻尼器参数α对梁端最大相对位移与阻尼器的吨位影响较小。但是不同C值下,曲线呈阶梯状,说明C值对梁端最大相对位移与阻尼器的最大阻尼力影响显著。
3.4 粘滞阻尼器参数的确定
由粘滞阻尼器参数的对比分析可知,C值越大,梁端最大墩梁相对位移越小,但是阻尼器的最大阻尼力也越大。从图8可以看出,C值从1 000 kN·(s/m)0.3变化到2 000 kN·(s/m)0.3,梁端最大相对位移仅减小了5 cm左右,但是阻尼器的最大输出阻尼力却增大了1倍。梁端最大墩梁相对位移及阻尼器最大阻尼力对参数α的变化不敏感,即α的取值对二者影响不大。对于主墩墩底弯矩来说,C与α有最优化值,当C取1 500 kN·(s/m)0.3、α取0.3时,主墩墩底最大弯矩有极小值,此时梁端最大墩梁相对位移为25.5 cm左右,阻尼器最大阻尼力为1 500 kN左右,阻尼器已经能很好的抑制结构纵向位移,并且阻尼器的最大阻尼力也不大。因此,综合考虑阻尼器的减震效果及经济效益,将 C为1 500 kN·(s/m)0.3、α取为0.3作为阻尼器最终的参数。
4 粘滞阻尼器的减震效果分析
将上述C与α值代入,取3条地震波,分析结构的地震反应,取各参数的最大值作为阻尼器减震下结构的最大反应。图10与图11给出了设置阻尼器前后梁端相对位移与主墩墩底弯矩的时程曲线,表2给出了设置阻尼器前后结构的地震反应计算结果。
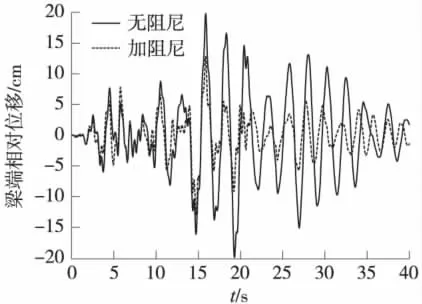
图10 设置阻尼器前后梁端相对位移时程曲线

图11 设置阻尼器前后主墩墩底弯矩时程曲线

表2 设置阻尼器前后结构的地震反应计算结果
图10及图11形象地反映了设置阻尼器后,梁端相对位移与主墩墩底弯矩显著减小,阻尼器对结构的地震反应有较好的抑制作用。由表2可知,2号与5号次主墩墩顶设置阻尼器后,次主墩水平力虽然为原来的2倍多,但是由于阻尼器耗能的功劳,墩底弯矩反而较未设置时减少了将近30%。主墩的减震效果较为明显,墩顶水平力减少了35%左右,墩底弯矩减少了38%左右。将主力与加阻尼器后的地震力组合并进行验算,发现主墩基础的承载力及桥墩桩基的配筋均能满足要求。设置阻尼器后,次主墩墩顶的墩梁最大相对位移减小量超过50%,梁端的相对位移减为原来的65%左右,最大单边位移不到13 cm,可以对梁端伸缩缝及边墩顶帽起很好的保护作用。
由图12知,阻尼器两端最大的变形为±100 mm左右,而极限温度+制动力+纵向风组合下结构最大静位移为±75 mm,考虑到一定的安全值,可将阻尼器的冲程定为±200 mm。C取1 500 kN·(s/m)0.3、α取0.3时,阻尼器的最大输出阻尼力为1 510 kN,兼顾安全并结合阻尼器的实际生产情况,所采用的阻尼器的最大阻尼力取1 600 kN。
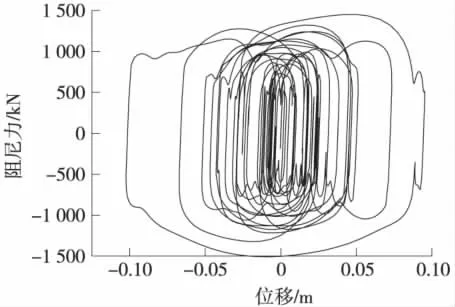
图12 阻尼器的力-位移曲线
5 结论
通过对金水沟特大桥设置阻尼器前后地震下的反应进行分析,得到如下结论。
(1)对于铁路高墩大跨刚构连续梁结构,地震力作用下,由于纵桥向承担上部结构地震力的桥墩较横桥向少,一般来说纵桥向的地震力更为控制设计。
(2)阻尼器参数的选取,应结合结构设计、减震效果及经济效益综合考虑。
(3)设置阻尼器后,全桥纵向的地震反应得到了很好的抑制,其中梁端的墩梁相对位移减少了35%左右,主墩墩底弯矩减少了38%左右,可以对梁端伸缩缝及边墩顶帽起很好的保护作用,主墩基础的承载力及桥墩桩基的配筋均能满足要求,确保了地震下结构的安全。
(4)阻尼器最终的参数选取及设置情况为:在每个次主墩墩顶设置4个最大阻尼力为1 600 kN的液体粘滞阻尼器,阻尼器的冲程为 ±200 mm,C值为1 500 kN·(s/m)0.3,α 值为0.3。
(5)高墩大跨刚构连续梁结构,由于桥墩较柔,地震下连续梁墩墩顶的墩梁纵桥向相对位移较大,适合采用液体粘滞阻尼器来进行减震。
[1]中华人民共和国铁道部.GB50111—2006 铁路工程抗震设计规范[S].北京:中国计划出版社,2009.
[2]中华人民共和国交通运输部.JTG/T B02—01—2008 公路桥梁抗震设计细则[S].北京:人民交通出版社,2008.
[3]刘振宇,等.南宁大桥粘滞阻尼器参数分析[J].桥梁建设,2007(4):26.
[4]王志强,胡世德,范立础.东海大桥粘滞阻尼器参数研究[J].中国公路学报,2005,18(3):38.
[5]斌 暄,王 磊,王歧峰.使用非线性粘滞阻尼器的桥梁在地震反应中的响应分析[J].公路交通科技,2007,24(10):77.
[6]魏锦涛.液体粘滞阻尼器及其在土木工程中的应用[J].四川建筑科学研究.2006,32(2):125.
[7]蒋建军,周红波.非线性粘滞阻尼器对悬索桥地震反应的影响[J].城市道桥与防洪.2004(6):100.
[8]陈永祁,耿瑞琦,马良喆.桥梁用液体黏滞阻尼器的减振设计和类型选择[J].土木工程学报,2007,40(7):57.
[9]蒋建军,蒋劲松.广西南宁大桥液体粘滞阻尼器设计[J].世界桥梁,2007(4):10.
[10]方 志.粘滞阻尼器参数对大跨度桥梁抗震性能影响研究[J].公路交通科技.2009,26(2):75.

