基于工装预变形的高速列车侧墙尺寸偏差控制方法＊

吴桃生，李志敏，王 华，冯孝忠，杨建华

（1 上海市数字化汽车车身工程重点实验室 上海交通大学，上海200240；2 唐山轨道客车有限责任公司，河北唐山063035）

高速列车可以满足长距离、大运量、高密度、短时间等运输需求，对国民经济发展起着举足轻重的作用［1］。侧墙是高速列车的车体关键大部件之一，其制造质量不仅影响着车体外观和车体总成的装配精度，也直接关系到列车行驶的安全性和可靠性。

侧墙由5块铝合金中空挤压型材焊接而成，变形规律复杂、各种偏差源高度耦合，尺寸偏差控制难度大［2］。当前，我国的高铁制造技术还处于起步发展阶段，缺乏一套行之有效的侧墙尺寸偏差控制方法，导致产品一次性成形合格率较低。实际生产中，只能依靠大量的火焰和机械调修来保证后续装配工序的顺利进行，这不仅增加了制造成本、影响了生产进度，更严重削弱了侧墙的强度和焊缝疲劳等性能。如何有效地控制侧墙等车体大部件尺寸偏差已经成为轨道装备制造企业迫切需要解决的问题之一［3］。

传统的尺寸偏差控制方法主要立足于偏差源的定位与诊断。如Hu等［4］针对汽车车门装配过程提出两级故障模式的在线分类方法，实现偏差源的定位；来新民等［5］建立了夹具假想失效的误差样本模型，利用失效映射程序，诊断出夹具的失效类型和偏差来源。王华［6］针对柔性薄板装配的特点，引入核函数PCA方法诊断装配偏差源。这类方法的特点是在检测和评价的基础上，确定各类偏差来源，再依据工程经验在实际生产中逐一加以控制。然而，由于高速列车侧墙的偏差源种类多样且高度耦合，变形规律非常复杂，要建立准确的偏差源诊断模型难度很大，导致上述方法在侧墙生产中的工程应用价值不高。

本文尝试在侧墙批量生产中，利用工装预变形来平衡其他偏差源的影响，实现对侧墙尺寸精度的控制。借助统计学手段，考察工装预变形量对侧墙轮廓尺寸的影响规律，利用多元回归方法建立侧墙尺寸偏差与工装预变形之间的定量关系模型，对该模型进行检验及修正，在此基础上，提出了基于工装预变形的侧墙尺寸偏差控制方法，并进行了工程应用，有效提高了侧墙的制造质量。

1 工装预变形与侧墙尺寸偏差定量关系模型

结合侧墙产品结构和制造工艺特点，分析了利用工装预变形实现侧墙尺寸偏差控制的可行性，在此基础上，应用多元回归方法建立了侧墙尺寸偏差与工装预变形的定量关系模型。

1.1 侧墙结构及制造工艺

侧墙由下墙板、窗下板、窗间板（若干块）、窗上板和上墙板等铝合金型材组焊而成［如图1（a）所示］。外形轮廓是侧墙的关键控制特征，控制的目标是使其尺寸处于设计要求的范围之内。侧墙外形轮廓表面为三维曲面，通过在侧墙不同断面上布置测点［如图1（b）所示］，以测点y向偏差来反映侧墙外形轮廓的尺寸偏差。

侧墙外形轮廓尺寸偏差的主要来源包括挤压型材本身制造偏差、焊接变形、工装夹具影响及工人操作影响等［7］。实际生产过程中，各种偏差源高度耦合，当出现质量问题时，几乎难以逐一、准确地实现所有偏差源的定位及诊断。生产实践表明，在上述各种偏差来源中，型材制造偏差、焊接变形及操作影响通常处于阶段性稳定的状态（同一批次型材尺寸波动趋势一致、标准操作下的焊接变形较为固定），在这种情况下，通过调整工装预变形量可以平衡其他偏差源的综合影响，提高侧墙的制造精度。

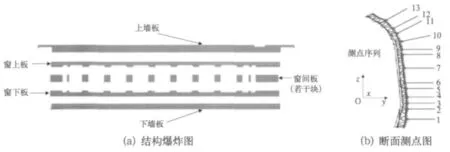
图1 侧墙示意图

工装预变形量指的是在一批侧墙生产之前，为获得更好的外形轮廓而实施的工装定位参数的调整量。侧墙组焊工装如图2所示，主要由12组y向定位支撑板组成，每组支撑板包括3块高度方向（y向）可调的小支撑板。所有支撑板的高度位置共同实现了侧墙外形轮廓的y向过定位，因此，支撑板的y向位置对侧墙外形轮廓有决定性的影响，通过合理地调整支撑板的y向高度，可以实现侧墙尺寸偏差的有效控制。

图2 侧墙组焊工装

1.2 基于多元回归法的模型建立

要利用工装预变形量实施精度控制，关键和难点在于如何建立准确的“尺寸偏差—工装预变形”模型，定量描述工装预变形量与侧墙外形轮廓尺寸偏差的关系，从而为后续的外形轮廓控制提供定量的数学公式。

在建模过程中，由于12组支撑板相互距离较大，对于侧墙每个断面，只考虑其对应的单组支撑板的影响。此外，相对于工装参数实际调整量，定位点磨损造成的高度变化可以忽略不计。

对任意一组支撑板，设3块小支撑板高度方向调整量（即预变形量）为 Δy1、Δy2、Δy3，调整后侧墙断面轮廓测点Pi处尺寸偏差为Hi，由前讨论可知，Δy1、Δy2、Δy3都会对Hi的值产生影响，为了准确地了解各支撑板对侧墙轮廓尺寸的影响规律，需要建立支撑板调整量与侧墙尺寸偏差之间的定量关系模型。多元回归方法常用于建立主变量与其多个相互之间不相关的原因变量（解释变量）之间的关系公式，比较简便、实用性很强［8］，因此本文采用该方法建立侧墙尺寸偏差与支撑板预变形量之间的模型，为保证模型的准确性及计算简易性，分别讨论了二次回归和线性回归两种情况。

多元二次回归数学模型为

多元线性回归数学模型为

式中i为侧墙断面测点序号；Hi为Pi测点y向尺寸偏差；H′1－i、H′2－i分别为二次及线性模型的Pi测点y向尺寸偏差估计值；ε1－i、ε2－i为其拟合误差；α及β为系数的估计值；Δyk为第k块支撑板预变形量。

为获取多元回归模型所需的样本数据，生产过程中需记录每组支撑板高度及所对应的断面测点尺寸偏差。表1以断面测点P7为例，列举了侧墙制造过程积累的20组数据。

表1 测点尺寸及对应支撑板高度变动量

基于表1数据，通过最小二乘回归可得式（1）、（2）的系数，从而得到测点P7尺寸偏差与支撑板预变形的多元回归公式。计算得到二次回归模型为

线性回归模型为

对于侧墙断面其余测点可采用同样的方法计算二次及线性回归公式，从而获得侧墙断面尺寸偏差与工装预变形之间的整体定量关系模型。

2 定量关系模型的验证与分析

对上述回归模型进行显著性检验、拟合误差分析和单因素子模型分析，在此基础上，针对二次及线性模型进行对比讨论。

2.1 模型验证

回归模型验证通常利用统计F检验及多重判定系数R2对其显著度及拟合优度进行验证，以证明模型的有效性。

首先对二次回归模型进行检验，通过分析模型方差对其显著性及适合性进行判断。设α＝0.05，回归模型方差分析如表2所示，其中，S为组间平方和（回归因子）以及组内平方和（残差误差）；M为平方和除以自由度得出的均方，查F分布表得临界值F－tab＝F0.05（9，10）＝3.02，因为F＝69.8＞3.02，所以二次模型显著度非常明显。计算可得到R2＝0.998 4，说明模型拟合优度非常良好。

表2 二次回归模型方差分析

依据同样的方法对线性回归方程进行验证，其回归因子自由度为3，残差误差自由度为16，查表可得F－tab＝F0.05（3，16）＝6.30，因为F＝1 999＞6.30，且R2＝0.999 9，所以线性模型显著度非常明显，模型拟合优度同样十分良好。

2.2 拟合误差分析

将表1中数据分别代入式（3）、（4），将计算结果与实际数据进行比对，可得到二次模型与线性模型的拟合误差，以此来分析两个模型之间的精度差异。

图3为20组数据下的二次及线性模型拟合误差折线图，可以看出，二次及线性模型的拟合误差均较小，都处于小偏差范围，从而再次验证了模型的有效性。此外，两种模型拟合误差趋势一致，虽然二次模型精度略高，但精度差异非常小。

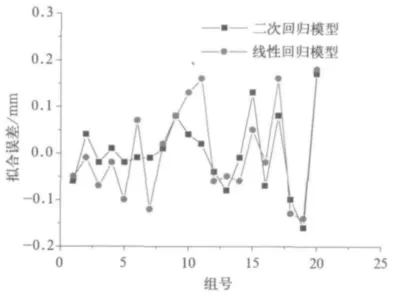
图3 拟合误差折线图

2.3 单因素子模型分析

将回归模型中的2个因素固定在零水平，或其他水平上，即可得到单因素子模型［9］。分别将式（3）和式（4）中的两个因素置零，可得到3块支撑板子模型。

获得的二次回归子模型为线性回归子模型为

图4为单因素子模型的回归曲线图。由该图可以看出：支撑板1，2的预变形量与测点P7的尺寸偏差正相关，即若Δy1、Δy2增大，则单因素影响下的测点尺寸偏差趋向于增大，支撑板3预变形量与其负相关，若Δy3增大，单因素下的偏差趋向于减小。其中Δy2对P7测点偏差的影响程度最大，Δy1最小。此外，在一定范围内，线性子模型与二次子模型曲线图形状差别很小，两种模型下工装预变形对侧墙尺寸偏差的影响规律相似。

图4 子模型回归方程曲线图

由上述所有检验及分析可知：

（1）侧墙轮廓尺寸偏差与工装预变形定量关系模型的拟合优度良好；

近年来，通信传输网络技术发展迅速，新技术层出不穷。日新月异的通信技术为建设坚强可靠的电力通信传输网创造了条件。目前，通信业界采用的传输网技术体制主要有 SDH，DWDM，ASON，OTN，PTN等。目前，国内地市电力通信网仍以 SDH 网络为主。

（2）两种模型拟合误差均较小，揭示的单因素影响规律相同，虽然二次模型精度略高，考虑到计算的简便性，在后续的尺寸偏差控制中，可以使用线性模型进行预变形量的计算。

3 基于工装预变形的侧墙尺寸偏差控制方法

3.1 尺寸偏差控制流程

将尺寸偏差—工装预变形定量关系模型应用于侧墙实际生产中，通过调整所需的工装预变形量以获得更小的尺寸偏差，实现对侧墙外形轮廓的有效控制。

基于工装预变形的侧墙尺寸偏差控制流程如图5所示。首先，在侧墙生产过程中采集20组检测数据，统计测点偏差均值为第m个侧墙上第i个测点的尺寸偏差）。然后计算偏差因子K值

其中T为测点公差；n为测点数量），其值大小反映侧墙轮廓与理论轮廓的偏离程度。若K＜1，则说明侧墙尺寸偏差处于可控的阶段，不需要调整工装进行控制。若K＞1，则表示侧墙尺寸偏差过大，外形轮廓质量不好，需要根据式（1）、（2）所得的模型计算工装预变形量，对下一批次侧墙进行尺寸偏差控制，并在控制过程中修正定量关系模型。接下来检测控制后的侧墙（20组）轮廓尺寸，循环以上过程，持续改进侧墙的制造质量［10］。

图5 侧墙尺寸偏差控制流程图

3.2 工装预变形量的计算

当侧墙轮廓出现较大偏差（K＞1）时，需要依据定量关系模型计算工装支撑板预变形量。理想情况下，为保证下一批次的侧墙能够有更好的外形轮廓，工装预变形引起的应该将实际偏差完全平衡、抵消，使经过调整之后实际轮廓尺寸偏差为零，即与应该大小相等，正负相反

对于式（4）取i＝3，7，12，联立可得三元线性方程组

将式（7）具体数值及回归系数β代入方程组（8），计算得到工装反变形量Δy1、Δy2、Δy3。

3.3 尺寸偏差控制及模型修正

在尺寸偏差控制过程中，应用3.2节计算得到的Δy1、Δy2、Δy3调整工装参数，可对下一批次的侧墙外形轮廓进行控制。理论上经过调整之后的侧墙轮廓尺寸偏差均为零，但由于工装预变形—尺寸偏差定量模型存在误差，调整后侧墙外形尺寸偏差依然存在，统计工装调整后侧墙各测点尺寸偏差均值计算 ΔH′i，将值与ΔH′i加入到表1中，更新数据后重新计算系数，可得到“工装预变形—尺寸偏差”修正模型。

循环3.2节与3.3节的计算过程，可将侧墙轮廓尺寸偏差控制在一个较小的水平，同时使得侧墙制造精度得到不断地提升。

3.4 工程应用效果

将上述方法在某轨道装备制造企业的侧墙工段中进行工程应用，取得了良好的效果。实际生产表明，利用工装预变形控制侧墙尺寸偏差的方法，对于提高侧墙制造精度，提升生产效率，稳定侧墙性能效果显著。

图6为工程应用实施前后的效果对比图，其中三维直方图的垂向坐标为测点尺寸偏差。

图6 尺寸偏差对比效果图

经过调整工装预变形对生产进行控制之后，侧墙最大偏差由3.21mm减小至0.98mm，平均偏差由1.81 mm减小为0.41mm，一次性合格率平均值由42.6%提升到81.3%，侧墙外形轮廓及制造精度得到了很好的控制。

侧墙制造精度的提高，不仅大幅度减小了人工调修的工作量，提高了生产效率、缩短了生产周期，还大幅度降低了火焰调修的温度及频率，使侧墙疲劳强度和刚度性能得到了有效提升。

4 结束语

（1）提出了一种基于工装预变形的制造精度控制方法，该方法简便有效，通过调整工装预变形量即可获得良好的侧墙外形轮廓；

（2）基于多元回归方法，建立了侧墙尺寸偏差与工装预变形的定量关系模型，并通过生产实践验证了该模型的可靠性及有效性；

（3）利用实测数据及定量关系公式计算工装预变形量，避免了生产控制对经验知识的过度依赖，为实现经验制造到科学制造的转变提供了基础；

（4）对于其他稳定、持续的产品制造过程，利用工装预变形平衡其他偏差源对制造精度进行控制的思路同样适用。

［1］董锡明.高速动车组工作原理与结构分析［M］.中国铁道出版社，2007.

［2］何华武.创新的中国高速铁路技术（上）［M］.中国工程科学，2007.

［3］张卫华，等.中国高速列车的创新发展［J］.机车电传动，2010，1（1）：1－11.

［4］Hu S.J.Stream of variation theory for automotive body assembly［J］.Annals of the CIRP，1997，46（1）：1－6.

［5］来新民.轿车白车身制造尺寸偏差控制关键技术研究［D］.上海：上海交通大学，1999.

［6］王 华.基于核函数PCA的柔性薄板装配偏差源诊断［J］.机械强度，2007，29（3）：433－436.

［7］周军年，等.轨道车辆用6005A铝合金型材焊接裂纹研究［J］.焊接质量控制与管理，2008，37（6）：49－51.

［8］张挠庭，等.多元统计分析引论［M］.科学出版社，1997.

［9］张烘州，等.响应曲面法在表面粗糙度预测模型及参数优化中的应用［J］.上海交通大学学报，2010，44（4）：415－420.

［10］林忠钦，等.轿车车体装配尺寸偏差控制技术［J］.中国机械工程，2000，11（11）：1 215－1 220.