速度200km／h车辆一系悬挂参数优化及性能分析＊

许自强，罗世辉，马卫华

（西南交通大学 牵引动力国家重点实验室，四川成都610031）

转向架的一系悬挂刚度对车辆非线性稳定性、曲线通过动力学性能影响较大。王开云等［1］基于机车车辆—轨道耦合动力学理论与TTISIM动力学仿真软件系统，研究了一系悬挂刚度对“天梭”号交流传动电力机车运动稳定性的影响。员华等［2］通过对地铁车辆转向架进行动力学建模分析，建议采用更优的一系弹簧刚度值及牵引杆的刚度参数，使列车在垂直方向的平稳性得以改善。陈康等［3］研究了一系、二系刚度对2B0架悬式动力车运行平稳性和蛇行稳定性的影响。倪平涛等［6］研究了一系纵向和横向刚度对轮对摇头振动的影响，得出了一系水平刚度的合理取值范围。

以上研究发现，增大一系水平刚度能改善轮对的蛇行稳定性，但对曲线通过不利，并在一定程度上影响横向稳定性。所以，对于车辆一系水平刚度的选择，应该在一个合理的范围内以保证转向架的直线、曲线及牵引性能［5－6］。

本文研究的转向架，采用转臂式轴箱作为一系定位结构。在实际设计中根据不同轴箱部件的选取，可以得到3种不同的一系合成水平刚度（表1）。3种不同的轴箱水平刚度中，哪一种为最优刚度难以确定。

1 动力学模型

该车辆为200km／h高速客车转向架，其最大轴重可达17t。车辆模型由1个车体、2个构架、4个轮对、8个转臂式轴箱组成、2个抗侧滚扭杆和2个Z字形牵引杆组成。每个构架和车体之间由二系悬挂装置连接，包括2个空气弹簧、2个抗蛇行减振器、1个横向减振器、2个垂向减振器；构架和轮对之间通过一系悬挂装置连接，一系悬挂装置由一系弹簧、与其并联的一系垂向减振器和转臂式轴箱组成。转向架与车体之间通过Z字形双牵引拉杆传递牵引、制动力，同时在车体和构架之间的抗侧滚扭杆装置起限制空气弹簧支承的客车车体相对转向架构架侧滚运动的作用。系统的惯性参数、悬挂参数及结构参数完全按照某动车系统的实际参数选取。车轮踏面为LM磨耗型踏面，钢轨为60kg／m钢轨。

图1 车辆模型

2 一系参数优化

2.1 总体优化法

根轨迹法是指当系统中某个参量由零到无穷大变化时，其闭环特征根在平面上移动的轨迹，以横坐标表示模态的实部（阻尼比），纵坐标表示模态的虚部振动频率（Hz）。本文将车辆速度设置为参数，考察在不同速度状态下转向架的稳定性特性，并通过根轨迹图找到临界速度，分析车辆的稳定性［7］。

首先基于根轨迹法对3个方案的优劣进行总体判定。3个方案的计算速度范围为100～400km／h，每隔10km／h计算一个点，共计算31点。3个方案的转向架蛇行根轨迹曲线如图2。由于根轨迹越小则车辆的稳定性越好，所以根据图2，初步断定方案3的参数比较合理。

表1 轴箱转臂节点的纵向、横向定位刚度方案

图2 3种方案的根轨迹曲线

2.2 刚度优化

在保持其他车辆参数不变的情况，分别改变一系定位的纵向和横向刚度，使得非线性稳定性临界速度符合优化目标的要求。该车辆运行速度为200km／h，非线性计算保证有20%的裕度的情况下，计算速度为240km／h。

横向刚度取8MN／m，变化一系纵向刚度的参数范围，从1～50MN／m，计算51次。计算结果见图3，除去蛇行频率急剧变化的点与阻尼比小于－5%的点，纵向刚度合理的取值范围在5～30MN／m，在此范围内车辆的非线性稳定性达到安全标准。

纵向刚度分别取14和28MN／m，改变横向定位刚度参数范围，从1～12MN／m，计算50次。做根轨迹计算，见图4。

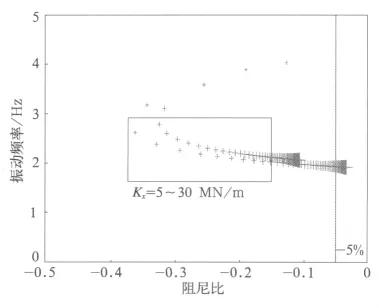
图3 改变纵向定位刚度的根轨迹曲线

图4 改变横向定位刚度的根轨迹曲线

从图中可以看出，当Kx＝28MN／m时，Ky只能取2～9MN／m，如果Ky取8MN／m，根轨迹接近－5%阻尼比。当Kx＝14MN／m时，Ky范围为2～12MN／m。这时Kx取8MN／m、7MN／m都是合理的。

综上所述，方案3的一系刚度方案为最佳。

3 车辆性能评价

3.1 非线性稳定性

在计算中，将车辆失稳后的模态作为初始状态，逐步降低其在理想直线轨道上的运行速度，用车辆各刚体横向振动的极限环判断车辆的横向稳定性［8］。

车辆的横向稳定性极限环计算结果见图5。车辆运行速度为260km／h时，轮对横向振动在1s后速度收敛。这表明该车辆的非线性稳定性临界速度为260 km／h，大于车辆实际运行速度的40%，满足运行要求。

图5 轮对横向振动极限环

3.2 轨道不平顺

轮对的纵向振动与轨道不平顺是有关系的，在整车模型和简化模型分析中采用了同样的不平顺，它由下列多项式表达

式中F（jΩ）为波形滤波器的传递函数，它与自身共轭函数F（－jΩ）相乘即为线路不平顺的功率谱密度函数；Ω为函数变量，物理意义为空间波数；b0，b1，a0，a1，a2则为多项式的系数。

通过多项式的系数可以确定不平顺的空间频率分布，并用一系列的正弦叠加得到时域不平顺。时域不平顺的生成中一个关键的因素就是采样点的选取，通过这个可以控制其精确性。本文计算时采用与我国干线不平顺相似的德国高速低干扰线路谱作为线路的不平顺输入。图6为60km／h时德国高速低干扰线路谱高低和方向时域不平顺。

图6 60km／h时的德国高速高干扰垂向和方向不平顺

3.3 直线平稳性分析

表2给出了该车在不同速度下前后两端平稳性指标的最大值。在德国高干扰谱激扰下，随着速度的增高，前后端平稳性指标呈单调增加的趋势，当速度达到最高250km／h时，车辆前端的垂向平稳性最差为2.75，也达到良好标准。其他工况下，平稳性指标达到良好或优的标准。

表2 车辆直线平稳性指标

3.4 曲线通过性能分析

曲线设置：直线段100m＋缓和曲线60m＋R300圆曲线200m＋缓和曲线60m＋直线。曲线超高120 mm，线路不平顺取2m平滑。由于计算中所取变量为未平衡离心加速度，因此计算结果也适用于其他半径的曲线，只是对应的通过速度将发生变化。

表3给出了所有工况下仿真计算得到的轮轨横向力、脱轨系数及轮重减载率等指标的最大值。在德国高干扰谱激扰下，随着未平衡离心加速度的增大，曲线通过安全指标也呈现单调增大趋势。当未平衡离心加速度为1m／s2时，轮轴横向力最大值达到27.99kN，小于其允许限值53kN。轮重减载率与脱轨系数分别为0.58和0.39，均小于安全限值。

表3 机车动态通过曲线时安全性指标最大值的仿真结果

4 结论

通过对该车辆转向架的一系刚度优化和动力学计算，得到以下结论：

（1）通过根轨迹法对某转向架的轴箱一系合成刚度进行根轨迹优化，发现方案3即纵向刚度Kx＝14 MN／m、横向刚度Kx＝7MN／m为最佳方案，在车辆的实际一系刚度设计中，推荐使用方案3。

（2）优化一系刚度后车辆直线运行的非线性临界速度为260km／h，是实际运行速度200km／h的130%，满足实际运行安全性要求。

（3）随着运行速度的增大，车辆前后端平稳性指标也在不断的变差，但是车辆的平稳性指标最差始终满足良好的标准，所以优化的一系合成刚度使车辆具有良好的运行舒适度。

（4）车辆通过小半径曲线时，各项安全指标基本达到良好。所以优化的一系合成刚度使车辆满足曲线通过安全运行要求。

［1］王开云，孟 宏，翟婉明.‘天梭’号电力机车参数优化及动力性能仿真分析［J］.机车电传动，2003，（11）：5－12.

［2］员 华，罗世辉.车辆悬挂系统参数选取对其垂向性能的影响［J］.都市快轨交通.2009，（2）：58－61.

［3］陈 康，罗 赟，金鼎昌.2B0架悬式动力车运行平稳性和蛇行稳定性［J］.西南交通大学学报.2003，（2）：28－33.

［4］倪平涛，姜建东，王开文.一系水平悬挂刚度对独立旋转车轮摇头振动的影响［J］.铁道车辆，2007，（4）：4－7.

［5］翟婉明.车辆—轨道耦合动力学［M］.中国铁道出版社，1996.

［6］张红军.高速动力转向架设计原则探讨［J］.铁道机车车辆，1996，（4）：10－13.

［7］罗世辉，金鼎昌，陈 清.轮对纵向振动与机车车辆相关问题研究［J］.铁道学报，2005，（6）：26－34.

［8］马卫华，罗世辉，宋荣荣.提速架悬机车动力学性能的改进［J］.西南交通大学学报.2007，（2）：84－88.