铁路货车动力学仿真分析与线路测试结果一致性研究

刘凤伟，张良威

（中国南车集团 长江车辆有限公司 产品研究所，湖北武汉430212）

为评估铁路货车的动力学性能，在设计阶段主要采用虚拟样机进行仿真分析和参数匹配。由于铁路货车动力学性能涉及的参数较多、离散性大、非线性强，一般仿真分析和测试结果会存在较大偏差。有必要进行分析和采取必要的措施，建立更科学合理的模型，提高仿真分析和试验的吻合程度，以提高仿真分析的准确度，更好地指导方案设计和解决复杂工程问题。要提高仿真分析和试验的吻合度，下述两点需要考虑，一是将试验条件特定化，例如车辆通过具有特定激扰的线路、线路保证干燥状态等；二是依据试验条件修正仿真分析模型，包括线路输入条件、车辆的部分参数以及连接力单元的等效方式等［1－2］。

相关研究表明，铁路货车动力学仿真模型验证主要从车辆系统中车体的固有频率、线路静态扭曲减载率、车辆通过特定波形线路的响应、车体加速度数值及加速度功率谱密度4个方面进行研究。下面以某出口窄轨矿石敞车为例，在线路试验的基础上，对上述4个方面进行分析。

1 模型建立

铁路货车为多刚体、多自由度的非线性复杂系统，其非线性运动微分方程为：

式中M为对角质量矩阵；X∈Rn，为N维坐标向量；F为系统的力向量函数，由系统本身的悬挂力、摩擦力以及轮轨力构成；v为车辆运行速度；F t为外界输入激扰力矩阵，包括轨道不平顺、风力、曲线半径、曲线超高和陀螺效应等引起的轮轨力和离心力。

1.1 模型假设

结合窄轨矿石敞车结构特点，建立模型时，进行如下假设：（1）铁路货车车体、摇枕、侧架和轮对均视为刚体，忽略各部件弹性变形；（2）忽略相邻车辆的相互作用；（3）假设轨道为刚性；（4）对库仑摩擦特性进行局部线性化处理；（5）轮轨蠕滑特性计算采用Kal ker简化理论编制的FASTSI M子程序。

1.2 仿真模型

窄轨矿石敞车动力学仿真模型由11个刚体组成。根据各刚体相互运动规律，轮对、侧架和车体均考虑6个自由度；另外，摇枕仅考虑垂向、侧滚和摇头自由度。各刚体间通过约束和等效力元进行连接。

建立模型时，将转向架考虑为子结构进行封装，并在主模型中调用两次该子结构。图1为该车辆系统的拓扑关系图，图2为该窄轨矿石敞车的动力学仿真分析模型，模型共计60个自由度，120个等效力元连接［3－4］。

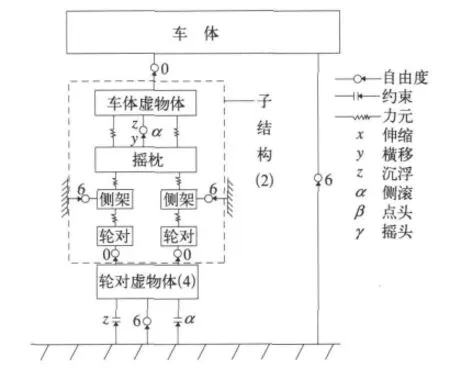
图1 车辆模型拓扑关系

图2 动力学分析模型

2 试验测试

2.1 线路静态扭曲减载试验

线路静态扭曲试验主要用于检验车辆对扭曲线路的适应性，特别是车辆通过缓和曲线时轮重减载情况。图3为该窄轨矿石敞车运营线路的扭曲减载试验条件，分为常规扭曲和组合扭曲线路两种，试验时测试减载最严重车轮的垂向载荷［6］。

图3 扭曲试验线路

2.2 线路动力学试验

窄轨矿石敞车于2010—2011年在澳大利亚昆士兰铁路完成了线路动力学试验，试验主要包括蛇行稳定性测试和循环轨道不平顺通过性能测试两部分。试验列车采用一台机车连挂两辆窄轨矿石敞车的编组模式，其中，空、重车状态车辆各一辆。试验线路由蛇行测试线路和循环轨道不平顺通过性能测试两段组成，蛇行测试线路部分为直线段和大半径曲线的组合，总长约9 km；循环轨道不平顺通过性能测试线路为3个特定、且左右交错的3个正弦波形，如图4所示［7］。

图4 循环轨道不平顺测试线路

蛇行稳定性测试数据来自空车，速度等级为40，60，70，80，88 km／h（车辆设计速度的110%）；线路循环轨道不平顺测试数据来自重车，速度等级为40，60，70，80 km／h（车辆设计速度的100%）。

3 模型修正方法

以上述试验测试结果为依据，进行了初始的动力学仿真数据对比分析。表明仿真数据与试验结果差异较大，特别是车辆系统的垂向沉浮和点头频率，以及循环轨道不平顺通过时弹簧挠度的变化，仿真计算结果较试验测试最大数值差异高达40%。

试验完成后，为分析仿真与试验结果的差异，提高动力学仿真的准确度，对悬挂系统的刚度阻尼特性进行了测试。图5为该敞车所采用控制型转向架的相对摩擦系数测试时载荷—挠度测试曲线，经多次测试，空、重车相对摩擦系数分别为0.229 8和0.026 4。根据测试结果，在仿真模型中将相对摩擦系数调整为与测试结果相同，相应转向架垂向总刚度由9.42 MN／m调整为8.16 MN／m［7］。除上述可测量的参数外，对系统各刚体转动惯量、输入条件及各接触面摩擦系数等参数通过重新计算进行调整。

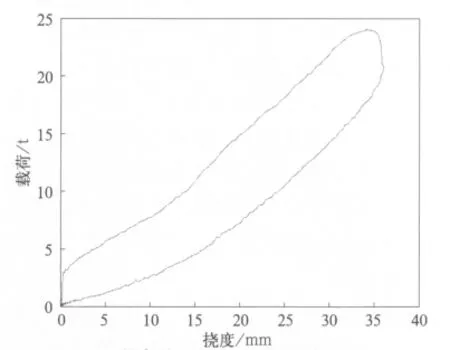
图5 常摩擦减振器减振特性曲线

4 修正模型仿真分析验证

按照上述修正后的模型，重新对车辆系统频率、线路静态扭曲减载率、车辆通过特定波形线路的响应等进行仿真计算，仿真分析与试验测试结果比较分析情况如下。

4.1 车辆系统频率

车辆系统无阻尼自振频率为系统本身固有属性，由系统本身决定。振动理论表明，当振动系统阻尼比ξ≪1，可忽略阻尼对频率的影响。根据试验数据分析，车辆振动系统阻尼很小，因此在对比分析试验数据时，忽略振动系统阻尼对频率的影响。

车辆系统中车体的侧滚、沉浮和点头振型为低阶模态，对车辆系统的动力学性能起主要作用。通过对窄轨矿石敞车动力学仿真模型线性化处理和求解，各模态振型如图6所示。

线路试验测试数据采用载止频率10 Hz的滤波，对各个速度级下的车体横向和垂向加速度进行频谱分析，车体侧滚、沉浮和点头模态频率的数据与修正模型后手动计算和仿真分析结果比较见表1。比较结果表明，仿真分析与试验数据偏差在10%以内。

图6 仿真模态振型

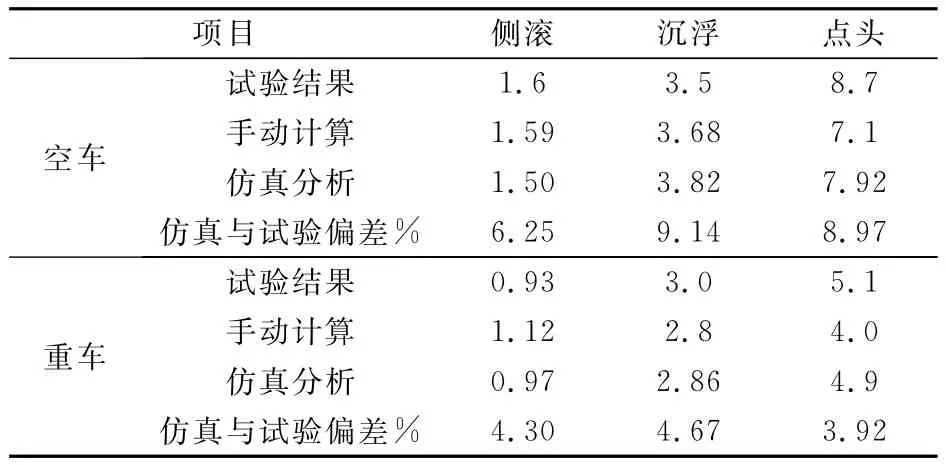
表1 系统频率比较 Hz

4.2 线路扭转减载特性

仿真分析时，车辆以5 km／h速度通过图3所示的扭曲试验线路，以模拟静态条件下车轮减载情况［6］。图7为减载量最大的车辆垂向载荷仿真分析曲线，由图7可知，车轮静态垂向载荷为18.26 k N，常规扭曲线路下，车轮最小垂向载荷为13.06 k N，减载率为0.284 8；组合扭曲线路下，车辆最小垂向载荷为12.38 k N，减载率为0.322 1。

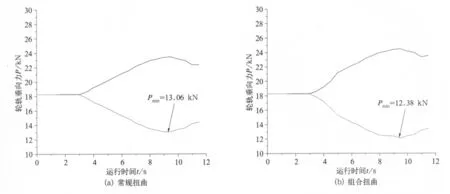
图7 减载特性计算结果

试验测试时，采用在车辆单侧加垫的方法，对减载量最大位置车轮垂向载荷进行测量。考虑货车转向架悬挂系统的干摩擦特性，采取调头、反复试验求均值等方式以保证数据的准确性。表2为扭曲试验最小车轮垂向载荷转换成车轮减载率后的结果比较分析，可知结果吻合程度较理想。

表2 减载率比较

4.3 蛇行稳定性

蛇行运动为横移和摇头的耦合运动，车辆发生蛇行失稳将严重影响车辆行车安全。该窄轨矿石敞车蛇行稳定性以空车状态下，车体心盘位置横向、垂向加速度的最大值和平均值进行评价。由试验测试报告可知，5个测试速度级下，88 km／h速度时车体的横向和垂向加速度最大。图8为车辆以88 km／h速度通过蛇行稳定性测试区段的加速度测试数据，数据采样频率为200 Hz。

因轨道水平、高低、方向和轨距不平顺的随机性，以及轮轨间摩擦系数的不确定性，使得仿真分析数据与线路测试数据存在较大差异。因此，以88 km／h速度级下，车体横向和垂向加速度的功率谱密度进行对比分析。

图8 车体加速度测试数据

图9 功率谱密度

由图9可见，车体横向加速度的功率谱密度图一阶频率仿真和试验数据偏差为5.26%，二阶频率偏差为4.32%；车体垂向加速度的功率谱密度图一阶频率仿真和试验数据偏差为7.22%，二阶频率偏差为4.23%。因此，仿真和试验数据分析所得横向和垂向功率谱密度图相近，主振型频率偏差在10%以内。

4.4 循环轨道不平顺通过性能

车辆通过图4所示线路，测试车辆滚摆性能，测试数据以弹簧偏差引起的减载量为主要评价指标。仿真和测试结果主要以中央悬挂弹簧最小压缩量进行比较。

由表3可见，中央悬挂装置弹簧压缩量具有近似的变化规律，且仿真和测试在对应位置的弹簧最小压缩量偏差最小为1.61%，最大为7.50%。

表3 弹簧最小压缩量 mm

4.5 结果差异影响因素分析

通过修正仿真模型和计算分析，仿真分析与试验数据偏差在10%以内，基本满足工程应用和用户要求［7］。分析造成以上偏差的因素主要有：

（1）仿真模型假设条件与实际车辆存在差异，比如车辆部件和轨道的刚体假设、忽略车辆相互作用等。

（2）车辆系统特性与实际车辆存在差异，比如各部件质量属性、摩擦特性、悬挂参数等。

（3）线路参数与试验测试条件存在差异，导致输入条件偏差，比如轨道实际曲线超高、轨道不平顺、三角坑及实际轮轨接触状态等。

在计算理论、模拟模型等与车辆实际状态基本相符的条件下，以上差异会导致一定程度的结果偏差。实践表明，上述因素对动力学性能的影响是相互关联和制约的。因此，在仿真计算时应尽量掌握车辆系统和试验线路条件的实际参数，并以此修正模型进行仿真计算。在产品研发过程中，一般实际线路试验条件不容易获得，但车辆系统的相关参数在样车完成后可以通过实测获得，对建立和修正动力学仿真模型有较为实际的意义。

5 结论

以窄轨矿石敞车为例，通过试验测试数据，对动力学模型进行修正和分析验证，可以得到如下结论。

（1）以线路试验数据为基础，通过修正仿真计算模型，车辆系统固有频率、车体加速度功率谱密度、轮重减载率、弹簧变形量等与试验测试数据偏差可控制在10%以内。

（2）为提高仿真结果与试验数据的吻合度，在完成样车试制后，应对系统刚度、摩擦阻尼、质量等参数进行实测，以此建立和调整仿真计算模型，保证仿真分析结果的准确度。

［1］严隽耄，傅茂海.车辆工程（第3版）［M］.北京：中国铁道出版社，2008.

［2］王福天.车辆系统动力学（第2版）［M］.北京：中国铁道出版社，1994.

［3］王 勇，曾 京，吕可维.三大件转向架货车动力学建模与仿真［J］.交通工程运输学报，2003，4（3）：30－34.

［4］王孔明，李 芾，卜继玲.货车转向架悬挂参数与运行性能研究［J］.铁道机车车辆，2005，25（5）：4－8.

［5］王 剑.出口澳大利亚磁铁矿石敞车［J］.铁道车辆，2011，（12）：21－24.

［6］陆冠东，徐荣华.线路扭曲与脱轨安全性分析方法介绍［J］.铁道车辆，2008，46（7）：1－4.

［7］David Hanson.ROAF Wagon Dynamic Testing Report［R］.Australia：SINCLAIR KNIGHT MERZ，2010.