基于混沌理论在股票预测中的应用
戴天虹,袁 博
(东北林业大学机电工程学院,哈尔滨150040)
混沌是一种低阶确定性的非线性动力系统所表现出来的非常复杂的行为,它对现代科学具有广泛而深远的影响,几乎覆盖了一切学科领域,尤其是在物理学天体力学、数学、生物学、经济学等方面得到了广泛的应用[1]。我国的资本市场是一个具有分形维结构的混沌系统[2]。对股票市场进行混沌分析首先要先进行重构相空间。
1 相空间重构
动力系统重建称为相空间重构。动力系统长期演化中任一变量的演化过程都包含了系统所有变量的信息,即通过单变量时间序列反向构造出原系统相空间结构。考虑系统的某一单变量时间序列 {xi|i=1,2,…,N},时间间隔选取为Δt,就可从单变量时间序列 {xi|i=1,2,…,N}分析系统所有变量发展演化过程,其中蕴藏着参与该运动的全部变量的演化信息在相空间反向重构得到分析。相空间重构可从一维扩展到多维,这样就能充分分析动力系统的所有信息。混沌系统有奇怪吸引子、分维数、正的Lyapunov特征指数等几个特征量。重构相空间就是通过选择合适的延迟时间和嵌入维数将原系统重构后,还原混沌系统的混沌吸引子,分析各个特征量。
Takens证明了一个合适的嵌入维,即如果延迟坐标维数m≥2d+1,d是动力系统的维数,利用原始系统中的某个单时间变量的延迟坐标来重构相空间,就可在重构相空间里把有规律的混沌吸引子恢复出来[3]。
设动力系统单时间变量x(t),t=0,1,2,…,N,选取嵌入维数m;延迟时间τ,则m维相空间矢量:
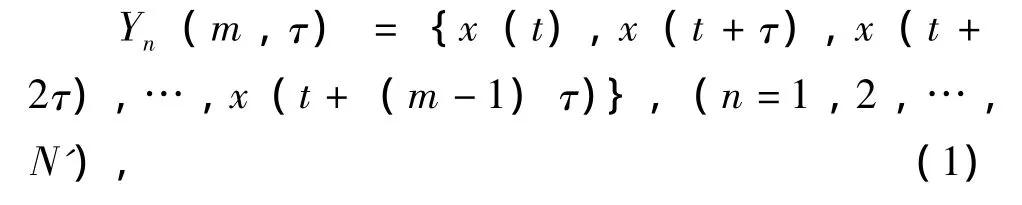
式中:m为嵌入维数;τ为延迟时间;N'=N-(m-1)τ表示m维相空间矢量的有效长度。
时间序列的相空间重构即由一维单变量时间序列重构出一个多维多变量的确定性相空间,即可把动力系统中蕴藏着参与该运动的全部信息发展变化重构出来。动力系统的相空间重构是混沌时间序列分析的基础,并以此可对重构后的相空间进行研究。
重构相空间目前广泛采用的延迟坐标状态空间重构法,即求取延迟时间τ和嵌入维数m之后,可按照公式 (1)对单变量时间序列进行重构其相空间。
本文重构相空间采用互信息函数方法选取单变量时间序列延迟时间τ,互信息第一次达到最小时滞时作为相空间重构的延迟时间 τ[4]。利用 CAO方法求取嵌入维数 m[5]。
2 混沌特性判定
混沌系统其对初始条件敏感的的依赖性,使动力系统中初始条件下微小的变化能带动整个系统的长期的巨大连锁反应。,这就是蝴蝶效应。这种局部不稳定性和对初始值的极度敏感性,被用来判断混沌的发生。另外,混沌吸引子通常都是非整数维的。如果序列中含有噪声,也会存在混沌吸引子为整数维的情况。所以通过计算关联维和最大Lyapunov指数检验混沌的存在[6]。
2.1 关联维计算
吸引子维数最常用算法为格拉斯贝格尔(Grassberger)和普罗卡恰 (Procaccia)于1983年提出的计算关联维数计算方法,称为G-P算法[2]。
G-P算法步骤如下:
(1)设x1,x2,…,xn为给定的一组反映系统状态的单变量时间序列,采用延迟坐标法,按照公式构造m维相空间。
yi= (xi,xi+τ,xi+2τ,…,xi+(m-1)τ)(i=1,2,…)式中τ为延迟时间。
(2)计算该状态空间中yi的关联积分

式中:ε为给定的常数;N是构造矢量个数,N=n- (m-1)p;‖yi-yi‖为yi,yj的范数,如取‖x‖=δ(x)为δ函数,δ(x)=
距离小于ε的矢量,称为有关联的矢量。关联积分是关联矢量在一切可能的N2中配对所占的比例程度。即n充分大、ε充分小时,关联积分:
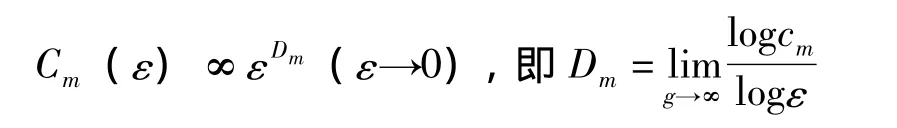
(3)对于ε的某一个适当范围,吸引子的维数D与关联积分C(ε)满足对数线性关系D(m)=ln C(ε)/lnε。
(4)重构向空间后,即可增加状态空间嵌入维数m,重复操作上述过程。如果单变量时间序列{xi}含有混沌吸引子,不断增大状态空间嵌入维数m,关联维数Dm也会随即增大,增长率会降低。状态空间嵌入维数m增大到一定程度时,Dm就在一定误差范围内保持稳定而不再增大,并向饱和值D收敛。由此计算出混沌吸引子的关联维数D。如果Dm不断增大且增长率也无序变化并不收敛于一个饱和值,则该系统包含噪声,是一个随机时间序列。
2.2 最大Lyapunov指数
混沌运动的基本特点是动力系统初始条件极为敏感,初始条件即使有细微的变化,动力系统的状态随时间演变的轨线就会以指数速度分离。Lyapunov指数就是定量描述这一现象的量。混沌系统具有整体稳定性和内在不稳定性。整体稳定性使混沌系统的运动轨道收敛到混沌吸引子上。内在不稳定性使系统在收敛到吸引子上的同时,某些方向上的运动又是不稳定的,导致系统对初始条件极其敏感。Lyapunov指数表示系统在多次迭代中平均每次迭代所引起的指数分离中的指数,是研究几何上相邻轨道以指数方式分离的快慢程度,反映了混沌系统局部范围内收缩与发散的速度。
对于n维动力系统而言,系统在每一维都存在一个Lyapunov指数,表示系统轨道在该维上的发散程度[5]。若一个初始条件为n维的无限小椭球体的长期演化过程,系统演化发生的局部变形使得小球体最终演化成n维椭球体,其中第i个Lyapunov指数LE可以用椭球体的第i个主轴长度li(k)来定义。即:

式中,{LEi|i=1,3,……,n}按照从大到小的顺序排列,称为Lyapunov指数谱,并将LEi称为最大 Lyapunov指数[6]。
如果时间序列的最大Lyapunov指数LEi大于零,就基本上可以肯定混沌的存在,最大Lyapunov指数值表明了系统的混沌程度[7]。
计算时间序列Lyapunov指数的方法主要分成两种:分析法和轨道跟踪法。轨道跟踪法是有A.Wolf、J.B.Swift等人提出并广泛应用的一种方法,该算法直接从Lyapunov指数的定义出发,跟踪系统的两条轨道,从而获取Lyapunov指数[8]。
3 数据分析
根据图1流程图对中国股票市场进行混沌判定,并仿真预测,并由1996.2.6~2005.12.6中国股票市场收盘价,共2 374个点。最高点:2 242.421。最低点:520.691。
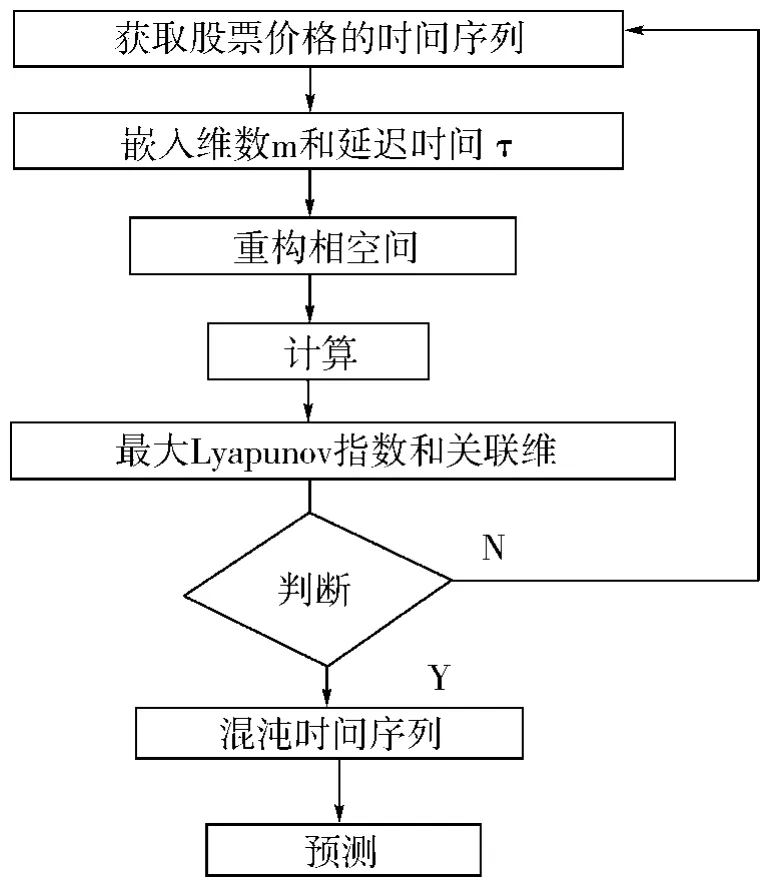
图1 流程图Fig.1 Flow chart

图2 1996.2.6~2005.12.6中国股票市场收盘价Fig.2 Closing price of China's stock market between 1996.2.6 to2005.12.6
根据图3所得,第一次达到最小值的时滞作为相空间重构的时间延迟τ,即τ=13。
由图4CAO方法计算混沌时间吸引子的嵌入维m可以看出,当m=9的时候,Ei不再变化,即m=9。

图3 互信息函数法确定延迟时间τFig.3 Delay timeτcalculated by mutual information method
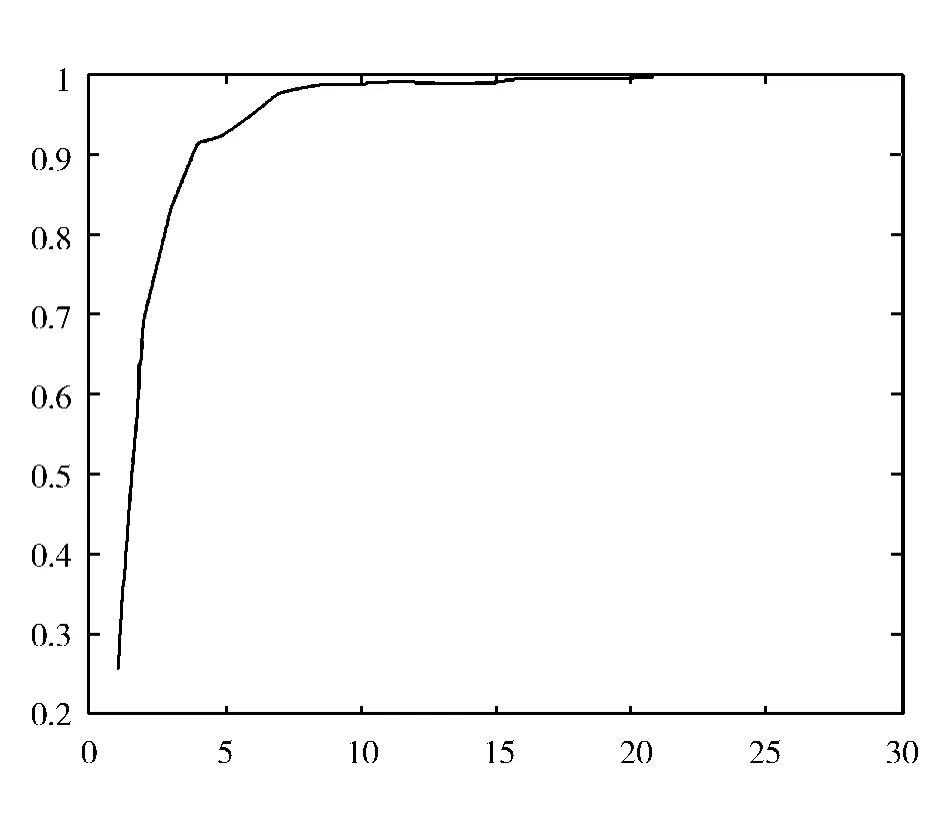
图4 CAO法确定嵌入维数mFig.4 Embedding dimension m computed by CAO method
由图5和图6可知最大Lyapounv指数数为2.342 2,饱和嵌入维数 m=14,关联维数为2.342 2。关联维数Dm=2.342 2为非整数,最大Lyapounv指数大于0,可以断定中国的股票市场是一个的混沌系统。收盘价最大Lyapounv指数LEi=0.078 8,因此预测时间为12.69 d。即可对股票市场可进行短期预测。通过MATLAB软件对其仿真,由图7可以看出,收盘价和预测值之间有些许误差。如仿真预测图7所示。

图5 最大Lyapounv指数Fig.5 Largest Lyapounv index

图6 GP法求关联维数Fig.6 Correlation dimension calculated by GP

图7 仿真预测结果Fig.7 The results of simalation and prediction
5 结束语
通过相空间重构,根据G-P算法计算的关联维Dm非整数,通过计算得到的最大Lyapunov指数LE1均大于零,由此可以得出我国股票市场是一个混沌系统。基于最大Lyapunov指数的混沌预测证明对其可以进行短期预测,通过MATLAB软件对其仿真。
[1]陈 敏,徐德智,罗庆云.时间序列相空间重构及其应用研究[J].计算机与信息技术,2005(11):9 -11.
[2]李建功.中国资本市场的混沌研究[D].大连:东北财经大学,2003.
[3]吕金虎,陆君安,陈士华.混沌时间序列分析及其应用[M].武汉:武汉大学出版社,1995.
[4]A M Fraser,H L Swinney.Independent coordinates for strange attractors from mutual information[J].Phys Rev A,1986,33:1134 -1140.
[5]张淑清,贾 健,高 敏,等.混沌时间序列重构相空间参数选取研究[J].物理学报,2010,59(3):1576 -1581.
[6]金 玲,刘长滨.我国建筑业增加值时间序列的混沌预测[J].土木工程学报,2008,41(8):99 -104.
[7]王东生,曹 磊.混沌、分形及其应用[M].合肥:中国科学技术大学出版社,1995.
[8]王 静,李丕仕.基于Lyapunov指数的高校图书馆图书借阅流量混沌预测[J].现代情报,2009,29(9):7 -10.

