大跨铁路斜拉桥索塔环向预应力布束方案计算比较研究

鲁志强，陈 松

(1.中铁二院昆明勘察设计研究院有限责任公司，昆明 650200;2.中铁二局集团勘测设计院有限责任公司，成都 610031)

1 概述

某在建铁路斜拉桥为双塔双索面钢桁梁斜拉桥，跨径81 m+135 m+432 m+135 m+81 m，边跨设置2个辅助墩，半漂浮体系，塔墩固结，塔梁分离，主梁与桥塔之间设置支座约束主梁竖向及横向位移，纵桥向设置锁定装置。主塔顺桥向为单柱式，横桥向为花瓶形(折线H形)，小里程主塔总高为190.0 m，大里程主塔总高为192.0 m，其中下横梁以上塔高123.5 m，塔冠装饰部分高8 m。塔柱采用空心矩形截面，纵桥向尺寸上塔柱为7.5 m、中塔柱由7.5 m渐变到9 m，主塔下塔柱由9 m渐变到13 m，横向尺寸上中塔柱为5.0 m，下塔柱由5.0 m变化到9.3 m，横桥向两塔柱中心距为18 m。主桥采用两片主桁，N形桁架梁，桁宽18 m，桁高14 m，节间距13.5 m，斜拉索布置为平行扇形双索面，采用环氧涂层高强钢丝索，全桥共56对斜拉索。钢桁梁上索距均为13.5 m，塔上锚固区索距为2.5～4 m，斜拉索倾角为 26.5°～65°，索孔直径0.377～0.402 m;上塔柱截面纵桥向边长7.5 m，横桥向边长5 m，顺桥向厚度1.4 m，横桥向厚度1 m，外侧倒角为0.6 m×0.6 m，内侧倒角为0.6 m×0.4 m，锚固部位设齿块与平面预应力钢束。主塔及斜拉索布置见图1。

2 钢束布置方案设计及计算特征点选取

(1)方案一:横桥向开口U形预应力钢束布置见图2，有限元模型见图3。

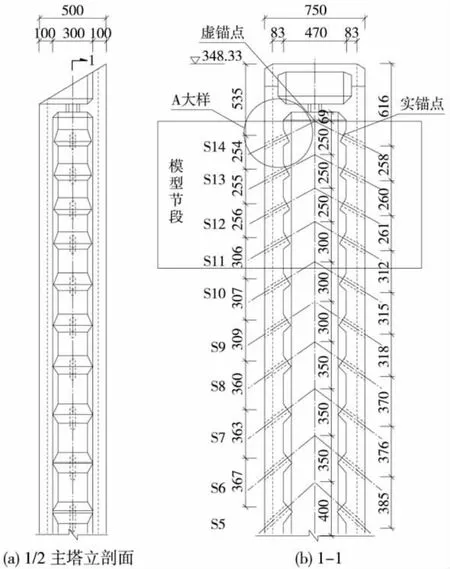
图1 主塔及斜拉索布置(单位:cm)

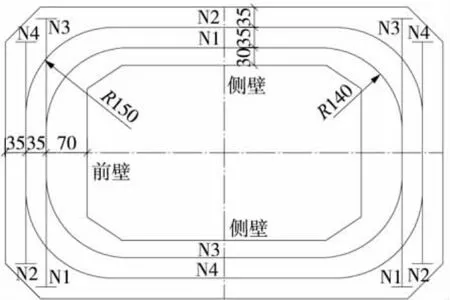
图2 横桥向开口U形预应力钢束布置(单位:cm)

图3 有限元模型

(2)方案二:纵桥向开口U形预应力钢束布置见图4，有限元模型见图5。

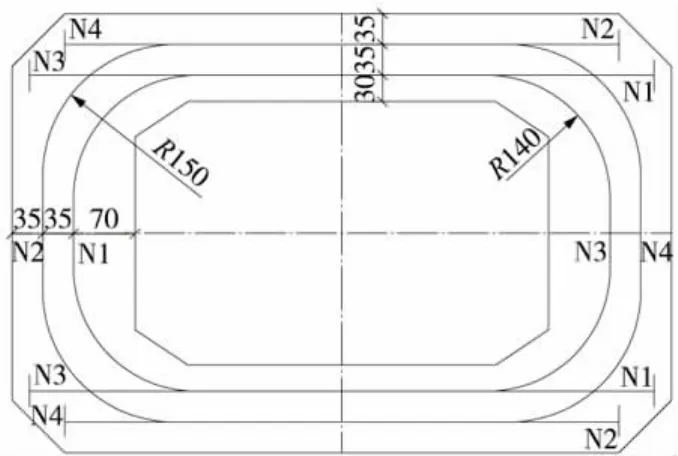
图4 纵桥向开口U形预应力钢束布置(单位:cm)

图5 有限元模型

(3)计算特征点选取

分析段有限元模型计算特征点[1]选取:截取分析段索孔中心处水平面，沿塔壁外侧、内侧及中间均匀选取若干点为计算特征点，选取结果如下(图6)。

外侧特征点:1，2，3，4，19，20，21，22;

内侧特征点:8，9，10，11，12，13，14，15;

中间特征点:5，6，7，16，17，18。

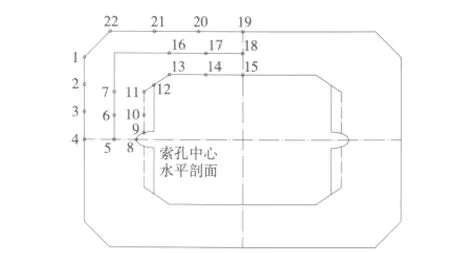
图6 索孔中心平剖面特征点选取示意

3 索塔空间有限元模型

3.1 模型参数取值

通过斜拉桥整体分析确定最不利荷载工况索力对应的索塔部位，分析时取该部位索塔节段来模拟。为了尽量减少模拟边界条件与实际情况差异，提高精度并减少计算时间，本次分析采用最不利索力对应塔段4个节段(即S11～S14)进行计算，计算节段共有4对斜拉索，相应立面有4段预应力钢束，不考虑索塔普通钢筋作用，最后取其中一个节段(即S12)进行分析研究[2]。混凝土和锚垫板、锚圈采用块体单元SOLID45模拟、混凝土用C50，弹性模量E取3.55×104MPa，泊松比为 0.2，密度为 25.5 kN/m3，线膨胀系数取0.000 01，锚垫板与锚圈取钢材弹模2.1×105MPa，密度为78.5 kN/m3，泊松比为0.3。

3.2 索力及边界条件处理

斜拉索索力按多种不利荷载工况及其组合中得到的最大索力取值;锚具采用LZM7-337，锚垫板尺寸为0.7 m×0.7 m，呈矩形状;预埋钢管内径0.38 m，锚圈外径0.47 m，锚圈高度0.2 m，拉索孔道斜向布置，拉索索力以面力施加在锚圈承压面上[3]。

考虑索塔节段本身及塔顶自重传递的压力，以面荷载施加在索塔节段模型顶面，对节段模型底部进行固结处理[2]。

3.3 预应力处理

预应力钢束作用采用LINK8单元模拟，以钢束单元节点和混凝土单元节点耦合的方式来模拟预应力筋与混凝土的共同作用。钢束采用高强低松弛钢绞线，标准强度为1 860 MPa，弹性模量为1.95×105MPa，U形束采用12-φ15.2 mm钢绞线，锚下设计张拉控制力1 302 MPa。按《铁路桥涵钢筋混凝土和预应力混凝土结构设计规范》(TB10002.3—2005)规定估算下列因素引起的预应力损失值:预应力筋与管道壁之间的摩阻，锚具变形及钢筋回缩，混凝土的弹性压缩，预应力筋的应力松弛，混凝土的收缩和徐变。将每根钢束分成若干段，分别计算各段钢束预应力损失，得到钢束各段有效预应力值，并以分段施加单元初应变的形式模拟预应力束对模型的作用。

3.4 计算工况

工况1:预应力+塔段自重;

工况2:预应力+塔段自重+主力+附加力组合最大索力。

索力按整体有限元模型计算分析取得，具体结果见表1。

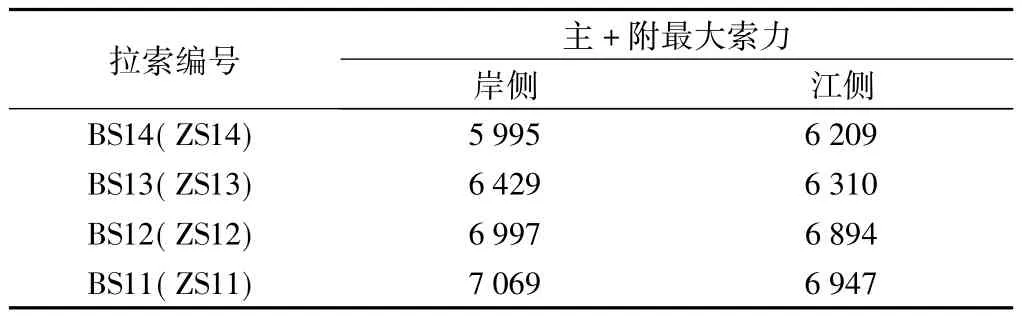
表1 最大索力 kN

3.5 有限元模型

实体及有限元模型如图7所示:每个节点3个自由度，其中X为纵桥向(侧壁方向)，Y为横桥向(前壁方向)，Z为竖向，长度单位为m，应力单位为MPa，S1为第一主应力，S3为第三主应力，其中符号规定:拉应力为正，压应力为负。

图7 索塔锚固区节段实体及有限元模型

4 计算结果分析

本文仿真模型为四节段三维有限元模型，在4对斜拉索锚固区施加相应大小的索力，但主要针对其中一个节段(S12)进行分析研究，以下计算结果均对应该节段模型。在上述2种荷载工况作用下进行了分析比较，主要针对工程上对混凝土设计较为关心的主拉应力和主压应力[3]。

4.1 横桥向开口U束布置计算结果

4.1.1 工况1作用下

(1)第一主应力(S1)分布

由图8可以看出，在预应力与自重作用下，除个别点第一主应力较大外，分析段第一主应力基本在0值附近，分布在－0.65～1.82 MPa。第一主应力较大部分主要位于斜拉索锚固齿块与内壁交界处。另外，钢束锚固点存在应力集中，由压应力过渡至拉应力，产生主拉应力，最大值达4.8 MPa，由于钢束预应力是直接作用在模型上，而实际工程中由于锚垫板的存在，故应力集中数值会大大减小。特征点第一主应力计算见表2。

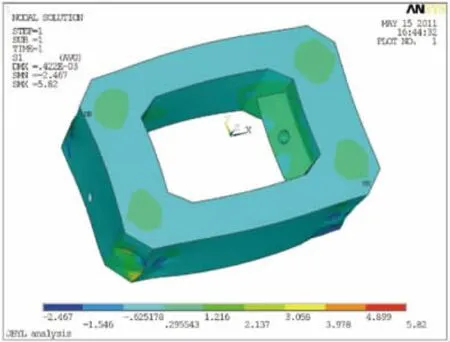
图8 第一主应力云图

表2 工况1作用下特征点计算应力值 MPa

(2)第三主应力(S3)分布

图9 第三主应力云图

由图9可以看出，在预应力与自重作用下，分析段完全受压。除个别点应力集中外，其他绝大部分第三主应力分布在－5.85～－1.77 MPa。很明显，侧壁内侧主压应力要大于外侧主压应力，而前壁则相反，外侧主压应力较大，斜拉索锚垫板下方区域主压应力最小。应力集中处位于外壁索孔上下缘附近，最大主压应力值达－16.8 MPa。特征点第三主应力计算见表2。

4.1.2 工况2作用下

(1)第一主应力(S1)分布

由图10可以看出，在预应力及自重与主+附组合最大索力作用下，第一主应力极小，除钢束锚固点外，绝大部分应力分布在－0.53～1.69 MPa，个别点应力较大，较大值出现于斜拉索锚固区域附近齿板上方。另外，钢束锚固点存在应力集中，产生主拉应力，最大值达4.7 MPa。由于实际工程中有锚垫板存在，故该应力集中值会较小[6]。特征点第一主应力计算见表3。

图10 第一主应力云图

表3 工况二作用下特征点计算应力值 MPa

(2)第三主应力(S3)分布

由图11可以看出，在预应力及自重与主+附组合最大索力作用下，分析段完全受主压应力。除个别应力集中点外，其他区域应力分布在－11.86～－1.71 MPa。应力集中点位于斜拉索锚固齿板锚垫板下方区域，主压应力最大值达－27.9 MPa，由锚固中心向四周扩散，应力逐渐减小。另外，前壁外侧，应力值明显小于内侧相应值。特征点第三主应力计算见表3。

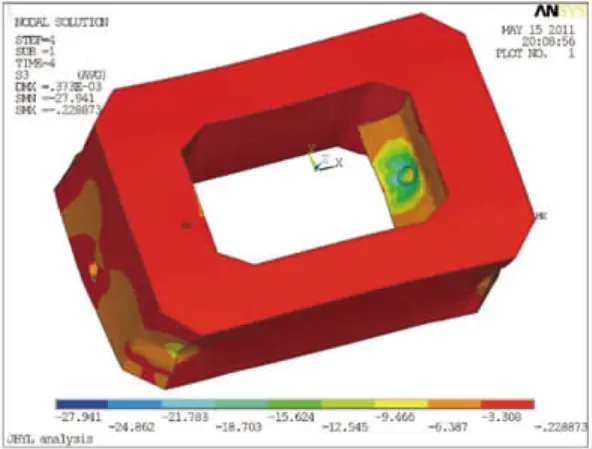
图11 第三主应力云图

4.2 纵桥向开口U束布置计算结果

4.2.1 工况1作用下

(1)第一主应力(S1)分布

根据图12可以看出，在预应力及自重作用下，除个别点第一主应力较大外，分析段第一主应力基本在0值附近，分布在－0.31～1.73 MPa。第一主应力较大部分主要位于斜拉索锚固齿块与内壁交界处。另外，钢束锚固点存在应力集中，由压应力过渡至拉应力，产生主拉应力，最大值达3.8 MPa，由于钢束预应力是直接作用在模型上，而实际工程中由于锚垫板的存在，故应力集中数值会大大减小。特征点第一主应力计算见表4。

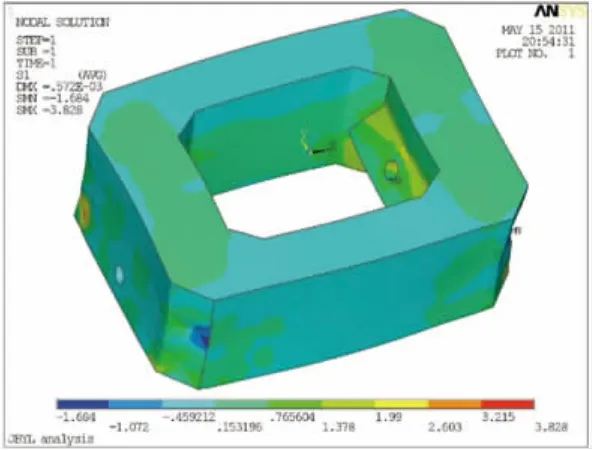
图12 第一主应力云图

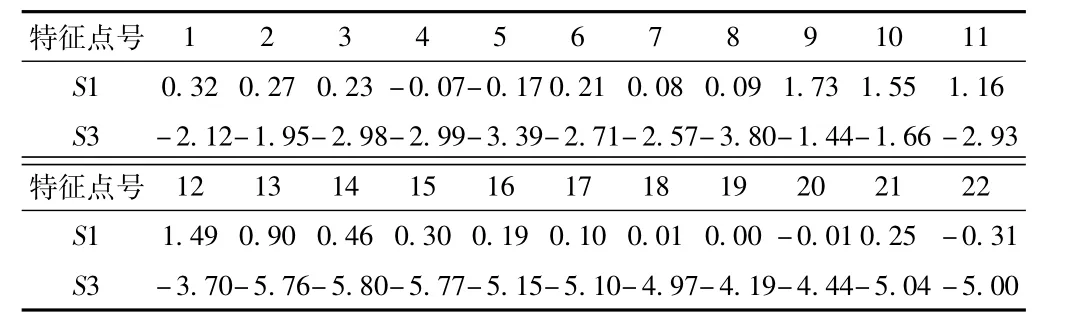
表4 工况1作用下特征点计算应力值 MPa

(2)第三主应力(S3)分布

由图13可以看出，在预应力与自重作用下，分析段完全受压。除个别点应力集中外，其他绝大部分第三主应力分布在－5.8～－1.4 MPa。侧壁内侧主压应力要大于外侧主压应力，而前壁则相反，外侧主压应力较大些，斜拉索锚垫板下方至齿块内壁交界区域主压应力最小。应力集中处位于外壁索孔上下缘附近，最大主压应力值达－8.9 MPa。另外，钢束锚固点附近出现应力集中。特征点第三主应力计算见表4。

图13 第三主应力云图

4.2.2 工况2作用下

(1)第一主应力(S1)分布

由图14可以得出，在预应力及自重与主+附组合最大索力作用下，除个别点外，第一主应力分布在－0.33～1.59 MPa范围内，第一主应力较大值出现于索孔与内壁交界部位。同时，钢束锚固点附近存在应力集中，产生主拉应力，最大值达3.6 MPa。特征点第一主应力计算见表5。

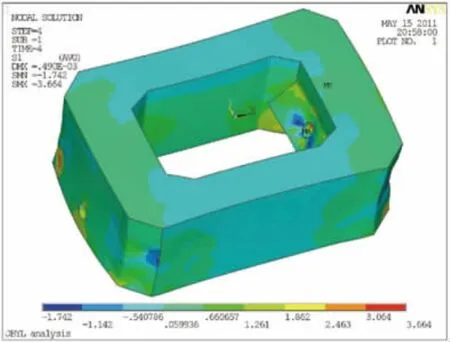
图14 第一主应力云图

表5 工况2作用下特征点计算应力值 MPa

(2)第三主应力(S3)分布

由图15可以得出，在预应力及自重与主+附组合最大索力作用下，分析段完全受主压。除斜拉索锚固锚垫板下方区域出现应力集中，最大主压应力达－28 MPa外，其他部分应力分布在－11.95～－0.65 MPa。显然，侧壁主压应力要大于前壁，并且应力值呈现两极分化。这与U束纵桥向布置的实际情况相符合。另外，前壁外侧中间区域，主压应力较小，需要加强。特征点第三主应力计算见表5。

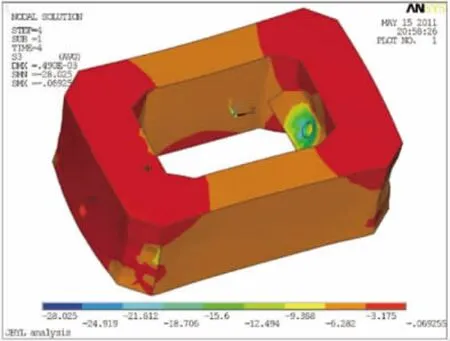
图15 第三主应力云图

5 2种方案计算结果对比分析比较

5.1 工况1作用下特征点计算结果对比

(1)第一主应力对比

根据图16可以看出，2种不同钢束布置方案下，特征点第一主应力分布趋势一致，并且应力值大小几乎相同。

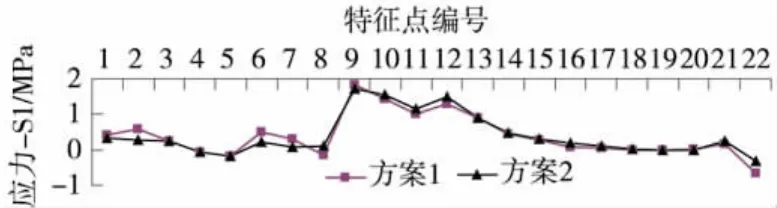
图16 工况1作用下特征点第一主应力比较

(2)第三主应力对比

由图17可以看出，在2种不同钢束布置方案下，特征点第三主应力变化趋势接近，且侧壁与前壁应力值相差都较大。很明显，方案二下侧壁特征点第三主应力较方案一特征点相应值大些，但前壁特征点第三主应力较方案二相应值大些。比较两种方案下前壁与侧壁应力值差异，方案一显得相对均匀些。

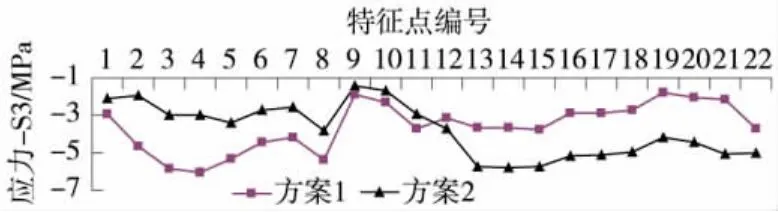
图17 工况1作用下特征点第三主应力比较

5.2 工况2作用下特征点计算结果对比

(1)第一主应力对比

由图18可以看出，在2种不同钢束布置方案下，特征点第一主应力变化趋势一致，应力值也几乎相同。

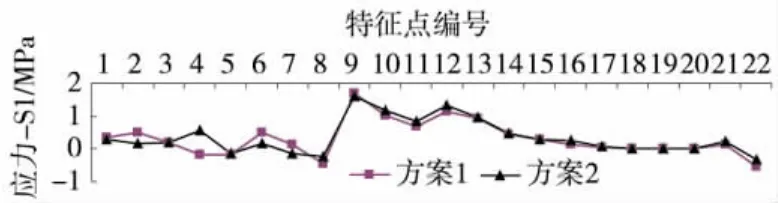
图18 工况2作用下特征点第一主应力比较

(2)第三主应力对比

由图19可以得出，在2种不同钢束布置方案下，第三主应力变化趋势一致，除索孔附近特征点应力值相近外，其他点应力值有明显差异。明显不同的是，方案一前壁特征点压应力较方案二相应值大，而侧壁特征点应力值方案二要大于方案一相应值。比较两种方案下最大最小值差异，方案一显得相对均匀些。

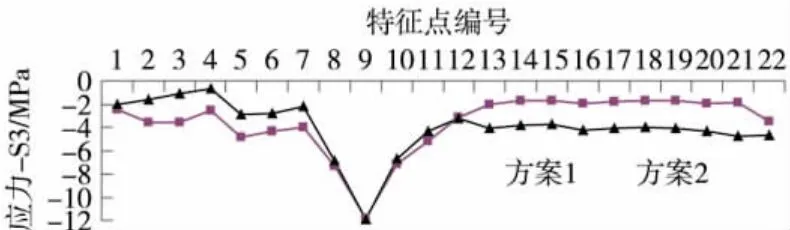
图19 工况2作用下特征点第三主应力比较

6 结论

(1)U形钢束横桥向开口与纵桥向开口2种布置方案下，分析段第一主应力分布趋势一致，且应力值差异极小。

(2)U形钢束横桥向开口与纵桥向开口2种布置方案下，分析段第三主应力分布有明显差异:方案一布置下，前壁第三主应力较方案二相应值大，而方案二布置下，侧壁第三主应力要较方案一相应值大。比较2种方案下应力值差异，方案一布置下，各部分应力值显得更均匀些，同时，方案一较方案二有更大的压应力储备。当索力吨位比较大，在满足侧壁压应力储备的情况下，前壁受力显得更不利，这时，宜优先选用方案一下钢束布置。

[1]邵旭东，曾田胜，李立锋，彭旺虎.斜拉桥预应力索塔优化布束方式研究[J].中国公路学报，2001，14(2):40-44.

[2]周立平.斜拉桥索塔锚固区应力方针分析[J].广东公路交通，2007(1):31-34.

[3]颜海.大跨度斜拉桥索塔环向预应力的有限元分析[J].上海公路，2003(4):24-27.

[4]贺立新.大跨径斜拉桥索塔锚固区应力分析[J].预应力技术，2004(5):21-23.

[5]梁柱，叶贵如.跨金华江斜拉桥索塔锚固区应力仿真分析[J].铁道建筑，2004(11):9-11.

[6]王新敏.ANSYS工程结构数值分析[M].北京:人民交通出版社，2007:487-489.

[7]李敏.斜拉桥主塔拉索锚固区锚下局部受力分析[D].哈尔滨:东北林业大学，2007.

[8]杨耀铨，朱玉.U形预应力束在斜拉桥索塔中的应用[J].国外公路，2001，21(3):24-27.

[9]余浪.斜拉桥锚固区应力分析研究[D].成都:西安:西南交通大学，2006.

[10]严少波，裴丙志.斜拉桥索塔拉索锚固区空间应力分析模型[J].国外公路，2000，20(3):22-24.