基于问题驱动的数学建模教学理念的探索与实践

郑 兰 肖文平

（1.武汉船舶职业技术学院，湖北 武汉 430050；2.华为成都研究所，四川成都 430072）

1 引 言

21世纪是科技创新的时代，在“十二五”时期，我国要继续保持经济的高速发展，离不开科技创新人才的培养，然而如何在数学教学中培养学生的科技创新思维和能力，一直是高校数学改革的重要课题。每年举行一次的全国大学生数学建模竞赛，是高校数学教学改革中的新思路。数学建模竞赛是培养学生创新能力和创新思维的一个良好平台，它是引导学生从“学得会”数学到“用得着”数学的一座桥梁。

全国大学生数学建模竞赛到今年也有20年的时间。传统的数学建模教学方法和传统的数学教学模式，即老师在台上讲，学生在台下听。这种方法的教学效果往往不理想，老师在台上讲的往往都是很深奥的数学基础理论或是数学理论方法的应用，学生听得很吃力，感觉很枯燥，没有调动学生的学习兴趣，遇到实际的数学建模问题时还是不知如何下手，教学效果往往不理想。

针对以上问题，我们在数学建模的教学实践中探讨和实践基于问题驱动的教学理念，学生感觉学习数学建模不是那么枯燥和深奥，并渴望能主动去思考问题，解决问题，课堂教学气氛越来越活跃，学生学习的热情也不断提高，取得了不错的教学效果。

2 问题驱动教学法的概念与内涵

恩格斯曾经说过 ：“和其他所有学科一样，数学是从人们的实际需要中产生的”，“纯数学是以现实的空间的形式和数量的关系为对象的。这些资料表现于非常抽象的形式之中，这一事实只能表面地掩盖它的来自现实世界的根源”［1］。这句话的意思是数学也是从实际的生活中产生的，是要满足人们的生活生产的实际需要，例如，我国古代的数学著作《九章算术》，它的九章中的每一章都是以实际问题为出发点，引出相关的数学理论。数学的研究和发展离不开实际问题的驱动，数学建模教学更是如此。

现代认知心理学关于思维的研究成果表明，思维通常是由问题情境产生的，而且以解决问题情境为目的。学生的创新意识正是在问题情境中得到激发的。

而问题驱动教学法的核心就是：教师在进行教学时，要精心设计问题情境，引导学生自觉、主动地去探索与分析问题直到最后解决问题。

基于问题驱动下的数学建模教学应该是在教师的引导下，先给出一个学生感兴趣和熟悉的实际问题，让学生主动思考，建立起数学模型，然后通过计算机相关软件计算出数学模型的结果，从而解决教师之前提出的实际问题，从而让学生获取数学知识、思想方法和技能。基于问题驱动下的数学建模教学法，充分体现了“学生主体，教师主导”的教学理论，通过学生的主动思考，主动解决实际问题，提高学生的数学建模能力。

2.1 以培养学生数学建模能力作为目的和核心

美国数学教授Davis在一篇题为《我们所做的数学是我们所教的数学吗？》［2］中尖锐地指出，现在多数数学教学中通常采取的授课路线是“演讲－记忆－测试”。他们很尖锐的指出我们教的数学已经严重偏离数学的本质。那么什么才是数学教学的本质呢？我们认为数学教学的本质是不断地提出问题并解决问题的方式来获取新的知识，培养学生的创新思维和创新能力的过程。而基于问题驱动的数学建模教学就是要学生在老师的指导下，以培养学生数学建模能力作为目的和核心，让学生通过主动思考、探索问题，获取数学建模的思想方法和知识技能。

2.2 突出学生的主体地位

实现以问题驱动教学法的数学建模教学，必须给学生一个自由思考，充分展现自己思维的空间。教师应该把学生放在整个教学过程中的主体地位，激发其能动性、自主性和创造性，自觉地以学生意识的增强、主体地位的确立、主体能力的提升和主体力量的解放为己任，只有这样学生才能积极主动地思考问题，解决问题，才能激发学生的学习兴趣，才能将学生培养成具有进取意识和创新精神的个体，并取得良好效果。

3 基于问题驱动教学法的数学建模教学的实施步骤

问题驱动体现了数学的创造本性。数学是一门具有创造性的学科，数学建模教学是培养学生创造性的阵地。问题意识和问题发现能力是创新精神的基石，发现问题是解决问题的逻辑前提，若数学建模教学要成为以问题发现和问题解决两者并重且相互促进的教学模式，数学建模教学一定会收到事半功倍的效果。

3.1 提出实际问题

问题驱动的数学建模的教学理念，第一步就是要提出实际的合理的问题，这是数学建模教学活动中的第一步，也是最关键的一步。提出的问题好，学生思考的主动性就高，就能充分激发学生的求知欲与学习的兴趣。那么怎样的问题才是好的问题呢？我们认为好的问题应具备以下几点：⑴应该从生产实际出发，是同学们熟悉的问题背景，使学生会觉得学数学建模有意思，有利于学生提高学习数学建模的兴趣，克服同学们对数学的畏难情绪。⑵问题应该不太难以理解和思考，做到学生容易上手，但是问题也不能太过简单，这样就失去了授课的价值。⑶应该能从问题中提炼出数学模型，并可以引出所需要学习的数学建模相关学科的知识。

例1：A1，A2是两个粮库，每月分别可以调出粮食30吨与40吨，三个粮店B1，B2，B3，每月的需求分别为20吨，25吨与18吨。粮库与粮店之间每吨粮食的运费如表1所示（单位：元／吨）。

表1 粮库与粮店之间每吨运费

问题1：要求安排粮食调运方案，在满足需求的前提下，使总费用最低。

首先，该问题通俗易懂，容易引起学生的兴趣和思考。另一方面，这个问题是运筹学上的运输问题，建立的数学模型是一个典型的线性规划，能够从该问题中引申出线性规划的理论和概念。

3.2 让学生主动思考，建立数学模型

学生能力的提高是数学建模教学的核心与最终目的，要达到这一点，我们必须以学生为整个教学环节的主体，教师在整个教学过程中起主导作用，也就是说，在教师的引导下，从实际的问题出发，让学生主动思考，主动研究，分析问题，建立起数学模型。尽管在整个教学过程中，学生是教学的主体，但教师在问题情境下的逐步引导也十分关键，教师可以通过设问的方法让学生逐步建立起正确的数学模型。如在例1中的，粮食运输计划问题。我们可以做如下的问题驱动。

问1：建立数学模型的第一步是假设合理的变量，列出目标函数。那么以上问题的未知量应该怎么设，目标函数应该是什么呢？

同学们就会想到要使总费用最低，必须先将粮库Ai到粮店Bj的调运量表示出来，于是同学们就会自然而然的想到设调运量为xij，i＝1，2，j＝1，2，3。目标函数为：

体现数学规划的数学模型过程的目的性，问题假设的合理性，参数选择的正确性。

问2：实际问题中往往由于生产规模，资源条件的限制，目标函数不可能无限大与无限小，一定有一些等式与不等式的约束条件，那么这个问题的约束条件应该是什么呢？

于是同学们就会想到每个月调出的粮食不应多于粮库的库存量即：

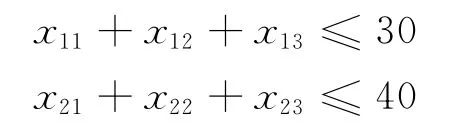
以及每个月运输的粮食应该满足三个粮店每月的需求即：

最后所设变量的非负约束：

体现了数学规划模型约束条件和目标函数相容性及数学规划模型的合理性，完整性。

问3：若问题中的资源约束改变或目标计划改变，最优解和数学模型会有哪些改变？

我们运用lingo软件求解时，由Solution Report中，可以看出第二行为紧约束，对应的对偶价格为2，表示该紧约束x11＋x12x13≤30，若变为x11＋x12x13≤31时，目标函数值就会从199变化为199加上2为201。

同时还可以从Solution Report中的Reduced Cost中看出决策变量有微小变动时，目标函数的变化率。另外，在LINGO｜Options中的Range选项中，我们还可以看到目标函数和系数变化范围等。由上述结果我们就引出了灵敏度分析的相关问题，这是线性规划的重要概念，体现数学建模结果分析和校正的重要性。

3.3 教师从问题中总结提炼，并引导学生求解数学模型

同学们在教师的指导下，通过对实际问题建立起数学模型后，一定要从中归纳数学理论与方法，这样学生才能真正在数学建模能力上有所提高。

上例中的粮食运输问题是线性规划中的基本问题之一。同学们所设的变量在运筹学中叫决策变量，总费用最低的数学表达式叫做目标函数，生产规模，资源条件的限制所形成的等式与不等式叫做约束条件。以上三个概念就是规划问题中的三要素，它体现了模型讨论的应用性和创新性。

4 结 语

思维通常是从问题产生的，并以解决问题为目的。问题驱动下数学建模的教学策略是在教师的指导下，从熟悉或感兴趣的数学情景出发，通过积极思考，主动探索，提出问题，分析问题，建立模型，最后解决问题，通过这一过程使学生获取数学知识、思维方法和技能、技巧并形成应用数学知识解决实际问题的能力。这种教学策略迎合了时代发展对创新人才的需要，同时实现了“从问题中来，到问题中去”的教学模式，提高了学生学习数学建模知识的主动性和积极性。

1 李大潜.关于大力提倡和推动以问题驱动的应用数学研究的建议［J］.中国科学基金，2006，20（4）.

2 林浩.用数学本原性问题驱动数学概念教学［D］.浙江：浙江师范大学，2007.

3 张奠宙，张荫南.新概念：用问题驱动的数学教学［J］.高等数学研究，2004（03）.

4 薛长虹，于凯.数学建模课程教学方式探讨［J］.大学数学，2007，（8）：4

5 钟守楠，高成修.运筹学理论基础［M］.武汉：武汉大学出版社，2005.