基于粗糙集和群决策的储煤中心选址方法

高太光，陈培友，马诗咏，赵文梅

(黑龙江科技学院经济管理学院，黑龙江 哈尔滨 150027)

近年来，因电煤价格快速上涨引起的电力供需失衡造成一些地区电力供应短缺，发电企业经营困难，从而影响了电力系统的安全平稳运行[1]。为了解决这一瓶颈问题，电厂与煤炭企业通过直接签订合同来保证电煤的供应，但受到各种因素的影响，经常会出现合同无法顺利签订或签订合同无法正常履行的情况。因此，可以建立储煤中心作为电厂和煤炭企业的第三方物流，这样不仅可以保证电煤的供应，而且还可以减少电厂的煤炭储量，节约电厂的成本，从而保证电力行业长期健康协调发展[2]。笔者综合运用粗糙集理论和群决策特征根法，结合专家的意见对多个储煤中心备选对象定性要素进行了综合评价，形成了较为客观和合理的评价值，为储煤中心选址决策提供了参考。

1 粗糙集的基本理论

粗糙集理论是1982年波兰科学家PAWLAK创立的一种数据分析处理理论，通过研究和应用实现了对决策中繁杂数据的有效约简，提高了决策的效率和科学性。粗糙集基本理论如下[3－5]:

(1)用四元组 S=(U，A，V，f)表示一个信息系统。其中:U为对象的非空有限集合，称为论域;A为属性的非空有限集合，A=C∪D，C∩D=Φ，C为条件属性集，D为决策属性集;Va为属性a的值域;f:U×A→V是一个信息函数，它为每个对象的每个属性赋予一个信息值。

(2)约简和核。设R是一个等价关系族，r∈R，如果IND(R－{r})=IND(R)，则称 r在 R中是可被约去的知识;如果P=R－{r}是独立的，则P是R中的一个约简。如果由于约简某一个或一组属性而产生新的不一致决策规则，则该属性或属性组即为核。利用区分矩阵可以较容易地计算出决策表的约简和核，约简是满足能区别由整个属性集区别的所有对象的属性极小子集，核是区分矩阵中所有单个元素组成的集合。

2 群决策特征根法

群决策特征根法是由邱菀华[6]提出的解决群决策问题的一种有效方法，它直接建立专家评分矩阵，相对于层次分析法而言，极大地简化了决策过程。它通过求出理想专家的评分向量得到被评价对象的排序，把与其他专家决策的差异性最小的专家设为现实中的理想专家。具体评价过程为:邀请几位专家对各评价指标的重要性进行打分，并将打分结果进行量化，从而形成专家的评分矩阵X，计算A=XTX，矩阵A的最大特征根对应的特征向量就是理想专家的评分向量，即为各评价指标的重要性排序值，对这些值进行归一化处理后即可得到各评价指标的权重值。

3 评价模型计算步骤

(1)构建决策表。根据专家意见，按设计标准对各备选储煤中心各属性打分，形成原始决策表。

(2)属性约简。利用区分矩阵对决策表进行处理，获得决策表的约简和核属性。

(3)原始数据的标准化。考虑数据处理的公平性和独立性，在决策矩阵参与运算之前要对其进行规范化处理[7]，笔者选用的数据标准化公式为:

式中:rij为第i个被评价对象的第j个评价指标经标准化后的值;xij为第i个被评价对象的第j个评价指标的原始值;

(4)约简后属性的评价。聘请专家对约简后属性的重要性进行打分，根据群决策特征根法对打分矩阵进行处理后，形成各属性的重要性排序值，并对排序值进行归一化处理。

(5)综合评价合成。根据指标权重和指标值，可采用线性加权法对各个指标进行加权计算，从而对各评价对象得出综合评价结果[8]，即利用式(2)得到各备选储煤中心的综合评价值，再按评价值的大小对其进行优劣排序。

式中:hj为第i个评价对象的定性综合评价值;pj为依据专家评分形成的各指标权重rij为标准化后第i个被评价对象的第j个指标的值。

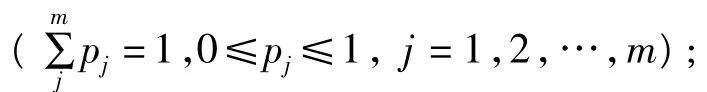
4 实证分析

储煤中心选址决策的确定应以电力和煤炭企业长期发展为导向，以建设与运营成本最低和收益最大化为基本目标，力争使储煤中心的具体分布与相关资源和需求分布相匹配。储煤中心的选址受到很多因素的影响，应结合实际情况对这些要素进行筛选。通过查阅相关研究文献，并与煤炭和电力企业相关负责人交流，确定储煤中心选址中关键影响因素包括大面积土地可得性、大面积土地地理位置、交通便利性、自然条件、社会负效应和对已有网点资源利用等[9－10]。为了适应某省电力和煤炭企业的发展需要，现有9个备选储煤中心地址(C1～C9)供其选择，根据专家意见所设计的决策表如表1所示。

表1 决策表

其中:用“好、一般、不好”3个等级指标评价交通便利性(c)、自然条件(d)和对已有网点资源利用(f);用“容易、一般、困难”3个等级指标来评价大面积土地可得性(a);用“高、中、低”3个指标评价社会负效应(e);用“市中心、城市边缘、远离城市”3个指标来评价大面积土地地理位置(b)。笔者采用3分法，用3、2、1分别表示“好、一般、不好”、“容易、一般、困难”、“市中心、城市边缘、远离城市”和“高、中、低”，用1和0表示“建物流储煤中心”和“不建物流储煤中心”的决策(y)。根据表1得到的区分矩阵如表2所示。

运用区分函数对表2进行处理后得到:

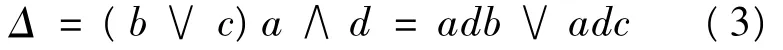
因此决策表存在两个约简{a，b，d}和{a，c，d}，核为{a，d}，冗余属性为 e和 f，约简后的属性指标集为{a，b，c，d}。应用式(1)对约简后的决策表进行标准化处理后得到的决策表如表3所示。

笔者聘请了该领域卓有成绩的5位专家对约简后指标的重要性进行评分，用3，2，1，0分别表示“很重要，比较重要，一般和不重要”。专家评分矩阵如表4所示。

依据群决策特征根法，用Matlab编程计算矩阵A=PTP的特征根，求得最大特征根ρmax=123.999 5，其对应的特征向量即理想专家的评分向量为:p=(0.566 9，0.368 7，0.526 2，0.515 6)，将p做归一化处理后得:p*=(0.287，0.186，0.266，0.261)，由此可得各评价指标的重要性排序为:a＞c＞d＞b。

应用式(2)对表3和归一化后的p进行处理，得到C1～C9这9个备选地址的综合评价值分别为:－1.193 0，1.878 2，－1.674 2，－1.684 0，1.312 7，－0.072 2，0.264 2，0.338 7，0.829 6。其排序为:C2＞C5＞C9＞C8＞C7＞C6＞C1＞C3＞C4。

表2 决策表对应的区分矩阵

表3 标准化处理后的决策表

从利用粗糙集和群决策特征根方法构建的综合评价模型的评价结果可以看出，9个备选储煤中心中C2的评价值最高，可认为是理想的地址，而C4评价结果最差，可以看作是最不适宜选址的。但由于受经济环境、企业长期发展与合作等需要的影响，模型评价结果仅作为企业选址决策的参考要素之一，另外还要综合考虑企业对储煤中心的具体建设和运营成本等。

5 结论

建立储煤中心是解决电煤供应瓶颈问题的有效途径，而科学合理地为储煤中心选址又是影响储煤中心建设效果的关键问题之一。笔者运用粗糙集理论和群决策特征根法，综合考虑影响储煤中心建设和运营的相关定性要素，构建了储煤中心选址定性要素评价模型，通过实证分析得到了模型有效性验证，评价结果与土地购置成本、设施建设成本、劳动力成本、煤炭配送成本和库存成本等定量综合考虑，可以实现将储煤中心建设运营与企业长期发展相结合，为决策提供较为有力的支持。

[1] 窦迅，李杨，高赐威，等.基于模糊综合评价的电煤供应安全预警机制[J].电力系统自动化，2011，35(1):29－33.

[2] 卢攀，刘泽剑，张鹏东.建立储煤中心的 KPCASVRM选址模型研究[J].电力科学与工程，2009，25(5):43－46.

[3] 张文修，吴伟志，梁吉业，等.粗糙集理论与方法[M].北京:科学出版社，2004:12－98.

[4] 初春，黄鲁成，卢文光.粗糙集赋权的服务企业竞争力模糊综合评价[J].武汉理工大学学报:信息与管理工程版，2010，32(3):465 －468.

[5] PAWLAK Z.Rough sets:theoretical aspects of reasoning about data[M].Netherlands:Kluwer Academic Publishers，1992:76 －108.

[6] 邱菀华.管理决策与应用熵学[M].北京:机械工业出版社，2001:285－289.

[7] 周建涛，陆海燕，叶新铭.面向资源调度的矩阵规范化方法研究[J].中山大学学报:自然科学版，2009，48(1):128－131.

[8] 李远远，云俊.基于粗糙集的综合评价方法研究[J].武汉理工大学学报:信息与管理工程版，2009，31(6):981－985.

[9] 高太光，陈培友.基于粗糙集和群决策的配煤中心选址模型研究[J].黑龙江科技学院学报，2011，21(3):257－260.

[10] 秦固.基于蚁群优化的多物流配送中心选址算法[J].系统工程理论与实践，2006，26(4):120－124.