基于小生境的菌群算法的改进
罗 熹,周 鑫
(武汉理工大学理学院,湖北 武汉 430070)
菌群优化算法(bacterial foraging optimization,BFO)是2002年由KEVIN提出来的一种基于大肠杆菌觅食行为模型的新的群智能算法[1-2],它是一种简单有效的随机全局优化技术,但是,基本BFO算法也存在精度不够高、收敛速度不够快的缺点。
在生物学上小生境是指特定环境下的一种组织结构。在自然界中,特征、形状相似的物种往往相聚在一起,并在同类中交配繁衍后代。小生境技术将每一代个体划分为若干类,在每个类中选出若干适应度较大的个体作为优秀代表组成一个群,再在种群中以及不同种群之间杂交、变异产生新一代个体群[3]。同时采用预选择机制和排挤机制或分享机制完成任务。加入了这种小生境技术的菌群优化算法(NBFO)可以更好地保持解的多样性,同时具有较高的全局寻优能力和收敛速度,特别适合于复杂多峰函数的优化问题。
1 菌群优化算法
菌群优化算法只能指导优化搜索,算法本身具备分布并行的寻优能力、较好的全局搜索能力,具有对初值不敏感的特点。2002年,KEVIN通过大肠杆菌的觅食行为,提出了BFO算法,其定义菌群行为包括以下4个行为:趋向性行为,聚集行为,繁殖行为和迁徙行为。其中趋向性行为又包括两个基本动作,即前进和翻转[4-5]。
假设要找到函数J(θ)的最小值,令j为趋向性行为的索引,k为繁殖行为的索引,l为迁徙行为的索引,并有如下变量假设:p为搜索域的维数;S为菌群总数;Nc为趋向性行为总步数;Ns为前进长度;Nre为繁殖行为总步数;Ned为迁徙行为总步数;Ped为迁徙概率;C(i)为在随机方向上进行翻转的步数。
令 P(i,k,l)={θi(j,k,l)}为每个菌群 S 内成员在第j次趋向性行为、第k次繁殖行为以及第l次迁徙行为时的位置。令 J(i,j,k,l)为第 i个细菌在 θi(j,k,l)∈ϑp位置时的成本。
下面给出BFO算法的4种行为的数学表示:
(1)趋向性行为。这个过程模拟了大肠杆菌的前进和翻转动作。大肠杆菌以两种方式进行趋向:根据给出的方向前进或进行一定角度的翻转;或者在趋向的过程中交替进行前进和翻转。根据以上假设,趋向性的过程可以用式(1)表示:
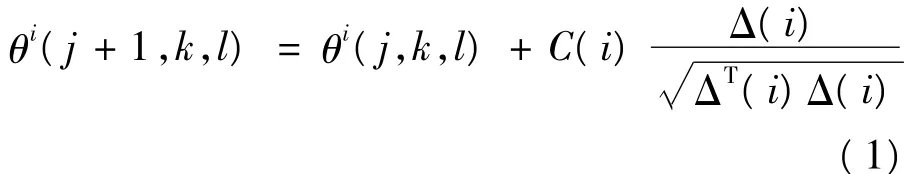
式中,Δ为随机方向向量,元素值域为[-1,1]。
(2)聚集行为。聚集行为是指一群大肠杆菌在受到外界刺激时,会产生一种化学物质,帮助它们聚集成群,使得群体密度增加,以抵抗外界刺激。这个聚集成群的过程可由式(2)表示:
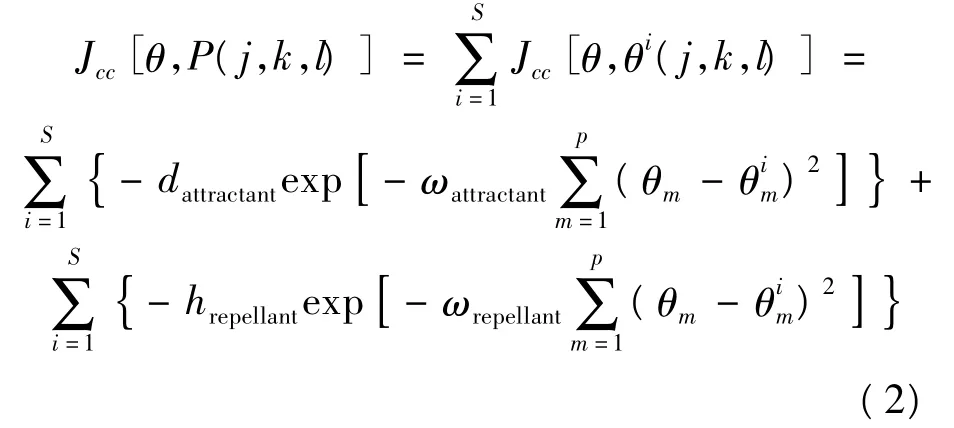
式中:Jcc[θ,P(j,k,l)]为需要进行最小化的目标函数,dattratant,ωattractant,hrepellant,ωrepellant分别为聚集系数和权重以及排斥系数和权重。
(3)繁殖行为。具有最小健康值的细菌最终将死掉,而更为健康的细菌则会生存下来,同时还会在同一个位置分裂成两个相同的细胞,并进行聚集等行为。
(4)迁徙行为。由于逐渐或突然的环境因素的变化,细菌会离开原有的环境,而出现在搜索域中新的区域内。在BFO算法中为了模仿这一行为,可以随机选择一小部分细菌,对它们的位置进行随机地重新赋值。
BFO算法对每个细菌、每次循环过程都要进行一次趋向性行为、聚集行为、繁殖行为和迁徙行为的运算,其算法的复杂度为o(n4),显然这样的算法收敛性是比较低的。且在BFO算法中考虑到细菌处理环境变化的一个过程,某些细菌可能会消失,但忽略了一部分细菌转移到其他地方可能导致原本的收敛点转移,从而降低BFO算法的收敛效率。
2 小生境及其与BFO算法的结合
小生境方法的基本思想来源于生物在进化过程中总是与自己相同的物种生活在一起的特点[6-8],反映到算法中就是使 BFO算法中的细菌个体在一个特定的生存环境中进化,小生境BFO算法(NBFO)可以避免在进化后期,适应值高的个体大量繁殖而充满整个群体。具体思想是:在每一代细菌进化前,根据细菌之间的距离找到每个细菌小生境子的种群,每个小生境子种群由距离相似的个体组成,然后由BFO算法更新。进化论中小生境概念是指生物在特定环境下的生存环境。其中“人以群分,物以类聚”反映了自然的进化过程,同种生物之间存在着优秀个体,不同生物之间存在着互相竞争和信息交换。“资源共享”体现在特定环境中共同生存的同种生物分享有限资源,互相协调达到共同进化。
小生境粒子群算法主要分为两个阶段:①小生境技术首先根据细菌之间的距离找到每个例子的小生境群体,然后利用菌群优化算法在每个小生境群体中进行位置和适应值的更新,其中菌群的群体最优值在该小生境群体中起作用;②对于更新后的群体,根据细菌间的距离,利用共享机制提高细菌的适应度,利用惩罚函数惩罚适应度低的个体,保留每个粒子群的最优个体,直到满足终止条件。
2.1 小生境群体的划分
对于细菌 θi(j,k,l)=(θi1,θi2,…,θip),i=1,2,…,S,它的小生境群体是计算该细菌与其他细菌之间的范数。
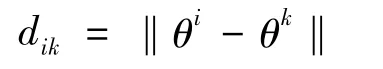
对于给定限制参数 σ0,如果 dik<σ0,k=1,2,…,S,则该个体加入到该小生境群体θig,这里范数一般对于实值函数取为欧式距离。
2.2 细菌间的共享函数
细菌i与细菌j之间的共享函数为:
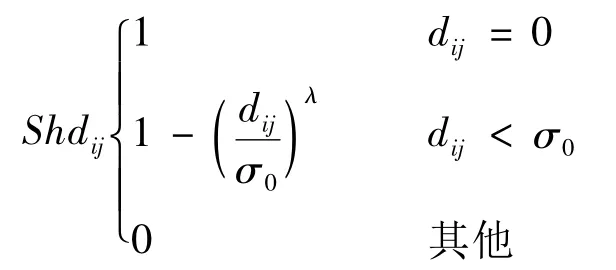
式中,λ为控制共享函数形状的参数。
2.3 适应值函数的更新
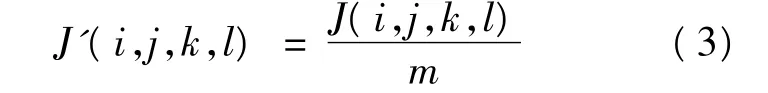
2.4 具体的算法流程
(2)按下列步骤确定小生境种群个体:①置i=1;②按照范数定义计算两个细菌之间的距离;③根据 dik<σ0,k=i,i+1,…,N,确定小生境群 θig,gi为θig的元素个数,其中σ0依据问题NFP而定。
(3)按照菌群优化算法对小生境群体进行速度和适应度更新:①初始化菌群算法各种行为的次数以及相应的参数;②按照菌群算法的趋向性行为更新各种细菌的位置、速度以及运动方向。其中群体最优值为小生境群体的最优值,不再是整个群体的最优值;③检查条件,对于更新后的个
式中体 θi(j+1,k,l)按照式(1)对 θi(j,k,l)中的第 i个细菌进行速度和位置的更新,得到个体的更新适应度;④细菌完成繁殖行为和迁徙行为;⑤利用更新适应度 J'(i,j,k,l)及惩罚函数 Penalty对该子群中低适应度的细菌进行惩罚,即当 θj,θk∈Mgi,‖xj-xk‖ <L,L <σ 时,比较两个细菌间的距离,并对其中适应度较低的细菌进行惩罚:Jmin(θj,θk)=Penalty,j,l=i,i+1,…,i+gi+1;⑥当 i+gi<N,置 i←i+pi,返回步骤②,否则,进入下一步。
(4)计算每个细菌的适应值,保留最优的适应值和个体,检查是否达到优化条件,如果达到误差精度,则结束,然后进入下一个细菌的小生境进行优化。
(5)若没有最优值,则将每一个细菌的小生境群体保留的最优个体组合成新的群体空间,并重复步骤(2)。
上述方法通过利用细菌间的距离划分每个例子的小生境群体,然后在小生境群体内利用菌群算法的进化机理对群体内的每个细菌进行更新。对更新后的群体,利用共享机制算法更新适应值,对于适应值最低的例子利用惩罚函数进行惩罚。
3 小生境菌群算法的性能测试
NBFO算法参数设置如表1所示。为了验证算法NBFO的有效性,将该算法用于优化测试函数 Shubert进行测试[9]:
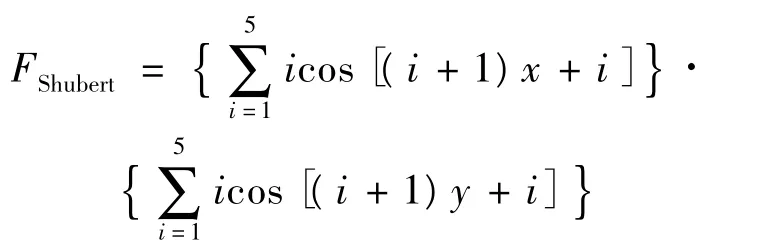
Shubert函数是极为困难的多峰值函数,函数在定义域 x,y∈(-10,10)上有760个局部极小值点,其中只有一个(-1.425 13,-0.800 32)为全局最小,最小值为-186.730 90。该函数极容易陷入局部极小值-186.340 00[10]。因此该函数仅含一个取最小值的解,Shubert函数在-10≤x,y≤10的函数图像如图1所示。NBFO算法寻找其最小值时的适应值曲线和BFO适应值曲线的比较如图2所示。
从图1可以发现NBFO算法在运行完毕之后所产生的细菌尽可能地聚拢在某几个最优值的点上,而从图2则可以发现NBFO在迭代到第2代时就已收敛到函数的最小值附近,然后菌群的最小值再产生微小的变化,并不断向最小值逼近。

表1 NBFO算法参数设置
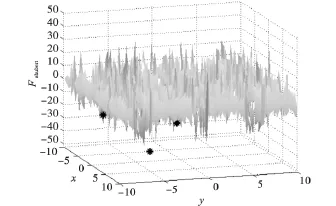
图1 Shubert函数NBFO算法细菌的最终分布位置
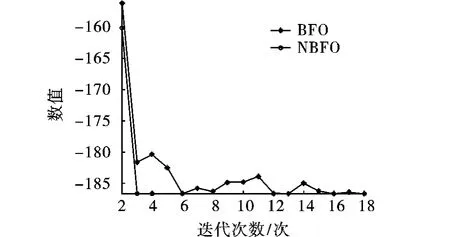
图2 BFO与NBFO函数迭代收敛图
表2给出了计算20次Shubert函数最小值时,BFO算法和NBFO算法的比较,由表2可知,原始BFO算法虽然没有陷入局部极小值-186.340 00,但由于全局寻优能力的不足,往往陷入了其他的局部极小值中,计算结果在-186.705 00左右波动。而NBFO的算法不仅可以收敛到最小极值点,同时运算的方差也远小于BFO。
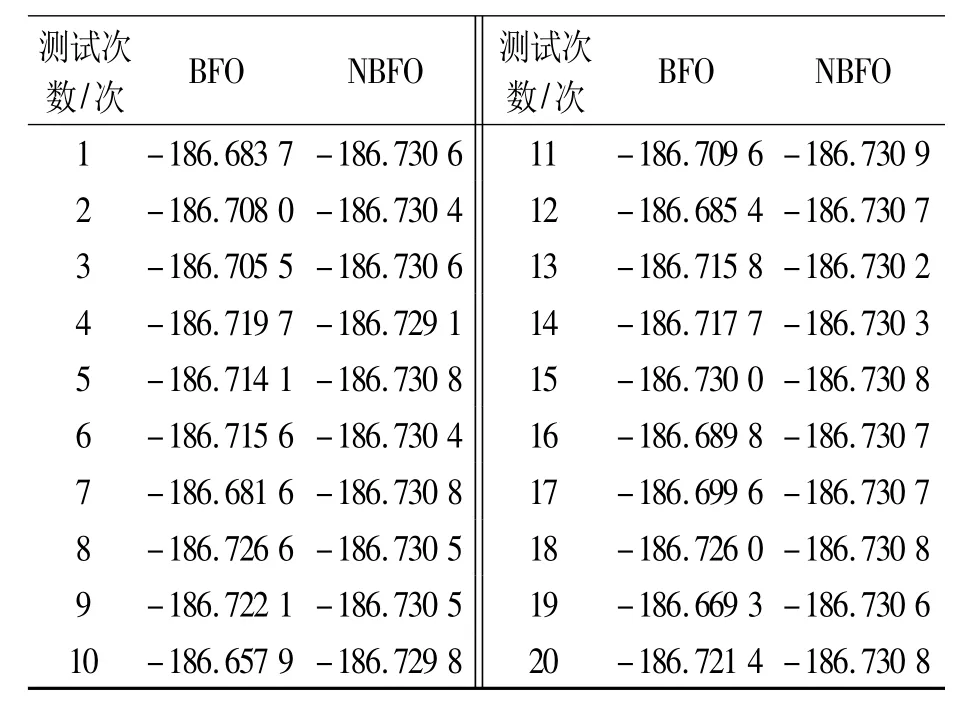
表2 BFO与NBFO在Shubert函数上的测试结果(σ0=7)
表3则给出了BFO算法和NBFO算法在其他测试函数中的表现,并用平均值和标准差,评价了BFO和NBFO的优劣。由表3可知,NBFO具有绝对的优势,能获得较好的解,收敛成功率高。但是,在实际计算过程中,由于NBFO的小生境技术导致了NBFO的时间代价相对稍高。

表3 多个优化函数测试表
4 结论
将进化论中的小生境技术与菌群优化算法结合,提出了小生境菌群算法,该算法在原菌群算法的基础上引入了共享机制,对菌群进行群聚分类,在经过BFO算法的演化后提取出适应度较高的细菌,组成下一代菌群进行迭代。该算法克服了菌群算法收敛效率低,容易收敛到其他极值点的问题。用Shubert函数验证了该算法的性能,并与原算法进行了比较,通过更多的优化函数(Rosenbrock、Rastrigin和Ackley)说明了该算法可以获得较好的解,极大地提高了收敛成功率。虽然该算法在原有算法的基础上增加了群聚的过程,但是由于每次挑出了适应度较大的细菌组成新的下一代菌群进行迭代,有效地减少了循环迭代的次数,在提高收敛率的情况下,付出的时间代价相对较小。
[1] 黄席樾,张著洪,何传江,等.现代智能算法理论及应用[M].北京:科学出版社,2005:54-87.
[2] 黄友锐.智能优化算法及其应用[M].北京:国防工业出版社,2008:56-98.
[3] 黄聪明,陈湘秀.小生境遗传算法的改进[J].北京理工大学学报,2004,24(8):675 -678.
[4] SWAGATAM D,ARIJIT B,SAMBARTA D.Bacterial foraging optimization algorithm:theoretical foundations,analysis,and applications[M].Berlin:Springer,2009:23-55.
[5] ARIJIT B,SWAGATAM D,AJITH A,et al.Stability analysis of the reproduction operator in bacterial foraging optimization[J].Theoretical Computer Science,2008,411(21):2127 -2139.
[6] 章军.小生境粒子群优化算法及其在多分类器集成中的应用研究[D].合肥:中国科学技术大学图书馆,2007.
[7] 周传华.小生境量子遗传算法及其在软测量建模中的应用研究[D].上海:华东理工大学图书馆,2007.
[8] 李孝源.动态环境下基于聚类的小生境微粒群算法的研究[D].湘潭:湘潭大学图书馆,2008.
[9] 周北岳,郭观七.引入适应值曲面结构的小生境遗传算法初探[J].岳阳师范学院学报:自然科学版,2002,15(1):59 -62.
[10] 周北岳,邓斌,郭观七.基于小生境技术的改进遗传算法的研究[J].机械强度,2002,24(1):13 -16.
——以贵阳花溪公园为例

