磁力泵中径向充磁磁力耦合器转矩的解析法计算

杜世勤

（上海电机学院 电气学院，上海200240）

磁力泵是一种由外磁与内磁转子配合、外磁转子通过磁力带动内磁转子转动、内磁转子带动泵轴转动，使泵体内泵轴上的叶轮转子完成转动工作的泵。一般情况下，内、外磁转子具有相同的磁极极对数。由于内、外磁转子之间有隔离罩形成密封腔，将输出轴和内磁转子封闭在密封腔内，既可防止流体向外部渗漏，又可冷却磁力传动装置（见图1）。

磁力泵结构紧凑、外形美观、体积小、噪声低、运行可靠，被广泛应用于化工、制药、石油等企业抽送酸、碱液、稀有贵重液、毒液、挥发性液体，特别是易漏、易燃、易爆液体物的抽送[1-2]。

图1 磁力耦合器的结构示意图Fig.1 Structure of radial field magnetic coupler

要设计一台磁力耦合器，其磁场计算和磁力转矩计算是一个关键的步骤[3-5]。研究永磁磁场和磁力传动问题的方法，一般归结为某些偏微分方程的求解。求解偏微分方程要结合具体问题中的特定边界条件才能获得唯一的解答，主要方法有电磁场解析法和数值分析法[6-9]。

电磁分布边值问题的数值方法包括有限差分法、有限元法等。采用数值计算法以后，针对实际工程问题的处理的思想方法也有了明显改变。过去要求尽可能简化物理和数学模型以求获解；而现在的目标是达到更合理的模型选择，以保证解的精确度，因此，往往选择比较复杂的模型。其中，有限元法占有绝对主要的地位，具有较大的应用范围。目前，使用有限元法求解的优势越来越显著[10-12]。但是，有限元方法一般要经过前处理、场计算和后处理等步骤，且商业软件的价格不菲，还需要专门培训人员操作。

电磁场解析分析法具有较长的历史，在早期就有很多文献利用电磁场解析分析永磁电动机的磁场参数以及性能。Gu等[13-15]采用解析方法计算永磁电机电磁场，对永磁电动机气隙磁场、永磁体边缘效应及开槽效应进行了研究。Zhu等[16-19]采用解析方法对永磁无刷直流电动机的空载磁场、电枢反应磁场、开槽效应以及负载磁场进行了系统的分析。上述方法已使用在永磁电动机的分析和设计之中，本文将解析方法应用于径向充磁磁力耦合器的磁场分析与转矩计算。两者都有永磁体磁场，不同之处在于电动机气隙一边是永磁磁场，另一边是电励磁，且开有齿槽；而磁力耦合器为双边永磁磁场，不受齿槽定位转矩的影响。

1 径向充磁磁力耦合器的解析法模型

利用解析方法计算径向充磁磁力耦合器的磁场和转矩，其主要特点包括：① 理论方面，概念直观，应用于比较特殊的边界条件下，解析法能获得精确的解，这对于理解场域中参数变化对磁场的影响很有帮助，并可借此进行场域中参数的调整。② 计算方便，虽然有的解析法所得的解冗长而复杂，以致难以手工计算，但现在可通过计算机得到其结果。因此，解析法和计算机应用相结合是一种有效的方法。③ 有限元方法是目前的主要计算方法，但该方法是在场域尺寸确定的前提下进行的，若先用解析法预测，将对磁力耦合器的分析和设计有所帮助。④ 在求磁力耦合器的电磁转矩时，有限元法对气隙区域的剖分有一定的要求，而使用解析法则相当方便。

1.1 步骤

当确立了由拉普拉斯方程或泊松方程描述的数学模型后，将进行边值问题的求解。分离变量法是求解边值问题的一种基本方法。当势函数随2个或3个坐标变量变化，且场域边界与坐标曲面一致的边值问题应用于求解拉普拉斯方程时，其具体步骤如下：

（1）根据问题给定的边界条件，选择适当的坐标系，给出边值问题在该坐标系中的拉普拉斯方程和定解条件。一般，若场域边界是平面、圆柱面、圆球面，则应分别选用直角坐标系、圆柱坐标系和球坐标系。

（2）将待求势函数进行分离，使之成为2个或3个函数（每个函数仅含一个坐标变量）的乘积，并代入拉普拉斯方程，从而将多变量的偏微分方程转化为2个或3个仅含单变量的常微分方程。

（3）由单变量的常微分方程的通解得到偏微分方程的通解，通解中含有待定的特征函数的特征值和待定常数。

（4）由边界条件确定待定的特征值和积分常数，得出边值问题的唯一确定解。

1.2 建立模型

采用极坐标系对径向充磁磁力耦合器进行分析，隔离套的材料为非导磁材料，等同于气隙，计算内、外磁转子产生磁场使用的物理模型见图2。

图2 单边励磁磁力耦合器示意图Fig.2 Coupler topologies of inner and outer rotors

图2中，Rro与Rmo分别为外磁转子磁钢外径与内径，Rmi与Rri分别为内磁转子磁钢外径与内径；g为等效气隙长度；变量θ为所在点与磁极中心线之间的夹角；M为永磁体的磁化强度；hm为磁钢厚度。分析中，假设内、外磁转子铁心的磁导率为无限大；永磁体均匀径向充磁，工作的第Ⅱ象限具有线性去磁特性，且M＝Br／μ0，其中，Br为磁通密度，μ0为空气磁导率。径向磁化强度分布如图3所示，其中，p为极对数。

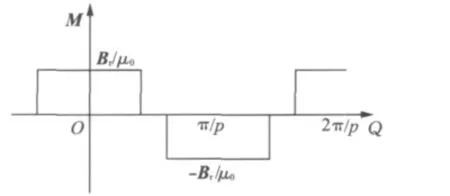
图3 径向磁化强度分布Fig.3 Radial magnetization

1.2.1 内磁转子模型 对应内磁转子模型，使用标量磁位φ求解，磁场强度

在气隙（区域Ⅰ）中，有

在永磁体（区域Ⅱ）中，有

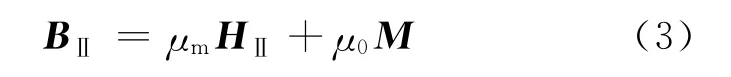
式中，μm为磁钢的磁导率。故得出标量磁位方程。在气隙中，

式中，▽2为拉普拉斯算子。在永磁体中，

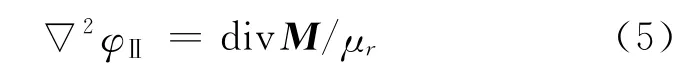
式中，μr为相对磁导率。

在极坐标下，对于径向均匀充磁，

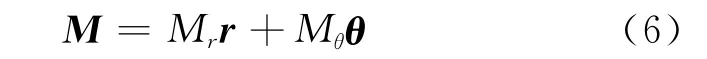
式中，Mr与Mθ为M中对应的2个分量，

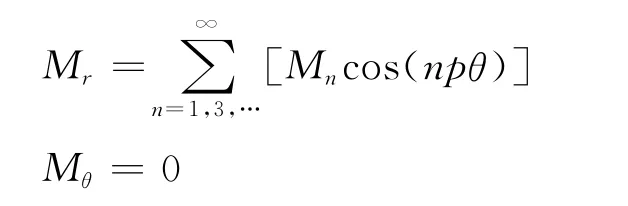
其中，为极弧系数。

由

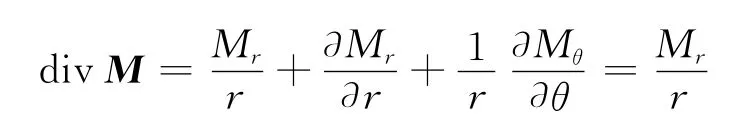
得标量磁位在气隙和永磁体中的数学模型，其中，r为半径。

在气隙中，

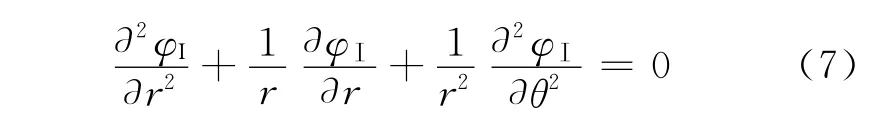
在永磁体中，

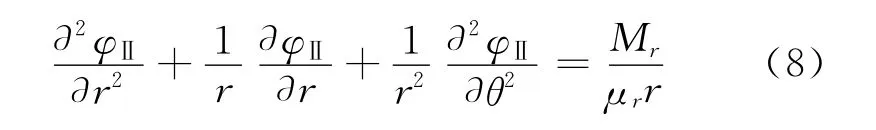
H中对应2个分量

式（7）～（8）满足以下2个边界条件：

根据数学模型及其边界条件得到标量磁位表达式，进而得到气隙中的磁密表达式。

当np≠1时，气隙中磁密分量为

1.2.2 外磁转子模型 相应地，对于外磁转子模型，可得到气隙中的磁密表达式如下。

当np≠1时，气隙中磁密分量为[16]：

根据上述内、外磁转子产生的气隙磁密表达式，结合磁力耦合器气隙都比较大的实际情况，且气隙为线性媒质，故2个转子之间气隙的合成磁场可使用内、外磁转子磁场分量的叠加来计算：

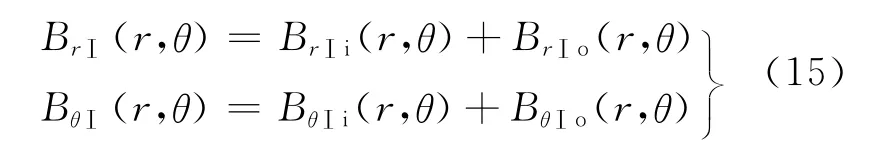
2 径向充磁磁力耦合器的解析法计算和有限元计算

有限元方法在处理复杂边界和非线性问题的磁场计算时，其应用的有效性和应用的广度已得到工程实践的验证，在磁力耦合器的设计中也被广泛使用[3-5]，本文作为验证软件使用。

本文以18极、工作转矩为200N·m、最大转矩为400N·m的径向充磁磁力耦合器的磁场计算为例，说明本文叙述解析方法的各种特点，同时给出相应的有限元计算结果用以比较。算例的具体参数如表1所示。

表1 磁力耦合器参数Tab.1 Parameters of a magnetic coupler

根据上述数据，针对内、外磁转子磁极中心线成90°电角的位置，采用解析法和有限元方法分别计算气隙中心的径向磁密分布，计算结果如图4所示。可见两者在形状和数值上相一致，但利用有限元方法计算时，由于气隙部分的离散不能无穷细化，磁密曲线的光滑性不如解析方法。

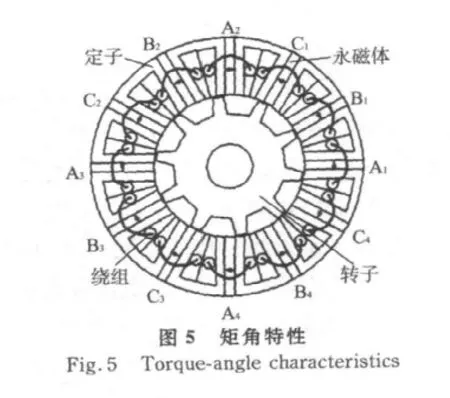
根据气隙中内、外磁转子的合成磁场的径向分量和切向分量，计算出磁力耦合器的矩角特性曲线如图5所示。图中，同样给出了有限元方法对同一算例的计算结果，转矩随转角的变化情况，解析方法计算得到的结果和有限元方法计算得到的结果是一致的。

3 结 语

磁力耦合器内、外磁转子之间由于具有较大的气隙，而且内、外磁转子具有规则的边界条件，较好地满足了采用解析方法计算的条件，可采用解析方法计算。算例中，解析法的得到的磁力转矩计算结果与采用有限元方法得到的结果相一致，简化了磁力耦合器设计的计算难度，提高了磁力耦合器参数变化对磁力转矩影响的预测能力。

[1] 杨建玲，许 伟，耿殿荣.磁力泵的特性与应用[J] .食品安全导刊，2010（8）：68-69.

[2] 闫雪兰，任振林，韩爱国.高碳有机酸磁力驱动泵的设计[J] .甘肃科学学报，2005，17（3）：69-71.

[3] 孔繁余，陈 刚，曹卫东，等.磁力泵磁性联轴器的磁场数值计算[J] .机械工程学报，2006，42（11）：213-218.

[4] 任振林，丁成斌，薛富连.磁力驱动器的有限元分析和优化设计[J] .甘肃科学学报，2006，18（4）：117-120.

[5] 王 瑜.永磁装置中磁场力的计算[J] .磁性材料及器件，2007（10）：49-52，60.

[6] 章名涛，肖如鸿.电机的电磁场[M] .北京：机械工业出版社，1988.

[7] 冯慈璋.电磁场[M] .2版.北京：高等教育出版社，2004.

[8] 王兴华，励庆孚，王曙鸿.永磁无刷直流电机磁阻转矩的解析计算方法[J] .中国电机工程学报，2002，22（10）：104-108.

[9] Muzhitskii V F，Kudryavtsev D A.Some problems in determining the optimum sizes of magnetizing systems based on permanent magnets[J] .Russian Journal of Nondestructive Testing，2004，40（2）：124-129.

[10] 胡之光.电机电磁场的分析与计算[M] .北京：机械工业出版社，1982.

[11] 傅为农，江建中.现代永磁电机的设计环境[J] .微特电机，1997（6）：37-40.

[12] 屠关镇.电机磁场有限元新技术[J] .电机技术，2007（2）：1-4.

[13] Gu Qishan，Gao Hongzhan.Effect of slotting in PM eletric Machines[J] .Electric Machines and Power Systems，1985，10（4）：273-284.

[14] Gu Qishan，Gao Hongzhan.Air gap field for PM electric machines[J] .Electric Machines and Power Systems，1985，10（5-6）：459-470.

[15] Gu Qishan，Gao Hongzhan.The fringing effect in PM eletric machines[J] .Electric Machines and Power Systems，1986，11（2）：159-169.

[16] Zhu Z Q，Howe D，Bolte E，et al.Instantaneous magnetic field distribution in brushless permanent magnet DC motors.Ⅰ：Open-circuit field[J] .IEEE Transactions on Magnets，1993，29（1）：124-135.

[17] Zhu Z Q，Howe D.Instantaneous magnetic field distribution in brushless permanent magnet DC motors.Ⅱ：Armature-reaction field[J] .IEEE Transactions on Magnets，1993，29（1）：136-142.

[18] Zhu Z Q，Howe D.Instantaneous magnetic field distribution in brushless permanent magnet DC motors.Ⅲ：Effect of stator slotting[J] .IEEE Transactions on Magnets，1993，29（1）：143-151.

[19] Zhu Z Q，Howe D.Instantaneous magnetic field distribution in brushless permanent magnet DC motors.Ⅳ：Magnetic field on load[J] .IEEE Transactions on Magnets，1993，29（1）：152-158.