突发灾害下带软时间窗多车路径搜索建模
刘天虎,许维胜,吴启迪
(同济大学 电子与信息工程学院,上海201804)
车辆路径问题(vehicle routing problem,VRP)是在满足一定约束条件下使适宜的行车路径达到既定的目标(如费用最小、耗时最短、行程最短等).而带时间窗的车辆路径问题(vehicle routing problem with time windows,VRPTW)则是在VRP问题上加上了访问需求的时间窗口.Desaulniers等[1]研究了具有等待成本的多资源站的VRPTW问题,得到了最优解.Qureshi等[2]提出了在软时间窗约束下的VRP搜索的精确最优解决方案,从而识别最短的行驶路径,控制最小的成本消耗.Ghoseiri等[3]对多目标的VRPTW搜索问题进行了系统研究,利用目标规划及遗传算法得到了最优路径解.为了求解VRPTW问题,过去的研究中最常用的算法有禁忌搜索算法[4]、插入启发式算法[5]、粒子群算法[6]、人工智能算法[7]、拉格朗日松弛算法、近似算法等,本文在以上研究的基础上,利用混合遗传算法(hybrid genetic algorithm,HGA)[8]研究当医疗救援站仅有1个时,如何调度多辆医疗救援车辆的最优VRPTW问题.
1 问题描述
突发灾害事件的发生往往对医疗救援活动提出急迫的需求,如何在有限的资源条件下实现最有效的救援问题越来越引起人们的重视,特别是如发生地震这样的灾害事件,要求医疗急救资源迅速做出响应,这就需要各个医疗救援站对救援车辆进行合理调度,然而一个医疗救援站不可能为所有的灾害点提供救援服务,而且每个灾害点在不同阶段的医疗救助需求也可能不同.本文需要解决以下2个问题:①当发生突发灾害事件时如何最小化救援的总成本.总成本的控制对救援站资源的使用效率将带来重要影响.②如何评价HGA算法在解决带软时间窗VRPTW搜索问题方面的有效性.需要深入分析寻优模型,并通过与精确算法数例仿真比较分析来说明其有效性.
2 模型的建立
实际救援中需要依据灾害点的特征及时调整救援路径,利用软时间窗作为约束条件比硬时间窗更加具有弹性,可以得到更加可行的解决方案.当灾害点不能在软时间窗的时限内得到及时救助时,引入惩罚成本,惩罚成本参数可以依据实际情况加以调整,通过权衡惩罚成本和使用额外车辆的固定成本,可以对医疗救援车辆进行合理调度.假定条件:①假定仅有1个医疗救援站为所属灾害点提供救援服务,救援车辆完成服务后需返回医疗救援站.②假定医疗救援站的车辆数及所有车辆的运载能力已知.③假定救援车辆与医疗救援站之间可以实现无障碍沟通,医疗救援站可监控所有救援车辆的所在位置,可以评估出救援车辆的行驶时间信息.
这里可以通过图1来说明软时间窗下的多车路径搜索问题.图中的第1个括号内的数值表示灾害点的x,y坐标方位,而第2个括号内的数值表示灾害点对医疗救援的需求量,而单车的最大承载量不能超过13个单位量;A0表示救援站;Di表示灾害点,i=1,…,13.
从图1a中可以看出,最初的灾害点有10个,有2部医疗救援车辆提供救援服务,车辆1的行驶路径为:A0→D5→D1→D9→D8→D6→A0.而车辆2的行驶路径为:A0→D4→D10→D3→D7→D2→A0.
当T1时刻车辆1行驶到灾害点D5,而车辆2行驶到D10时,此时收到医疗救援站的最新信息,又有4个灾害点D11,D12,D13,D14需要救助,从图1b可以看出,在规划的路径范围内,灾害点D11和D13可由车辆1提供救助,而灾害点D12和D14可由车辆2提供救助,在不超过车载容量的前提下,对2部医疗救援车辆的后续行驶路径进行了优化,车辆1后续行驶路径优化为:D5→D13→D1→A0,A0→D11→D9→D8→D6→A0,车辆2后续行驶路径优化为:D10→D3→D14→A0,A0→D7→D12→D2→A0.
从以上的分析可以看出,软时间窗下的路径搜索问题实际是一个混合整数线性规划,于是可以建立相应的数学模型,模型的目标是为了最小化救援的总成本(包括车辆成本、路径成本和惩罚成本).而该模型的限制条件由车辆、路径、灾害点时间窗所约束,于是可以建立模型的最优方程z如下:
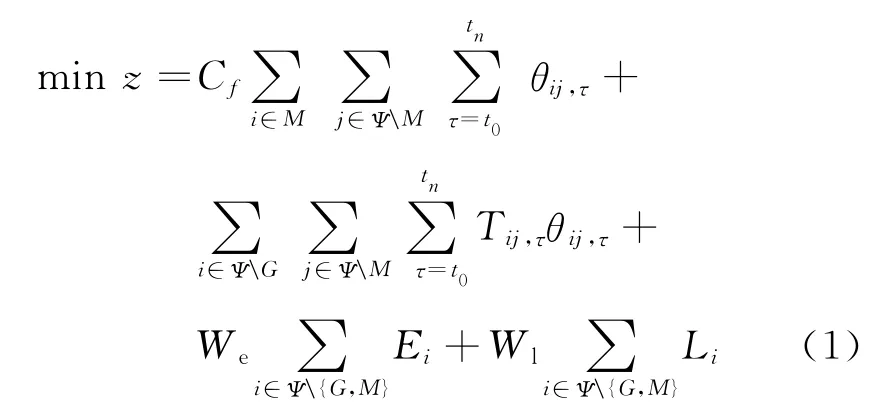
限制条件如下:
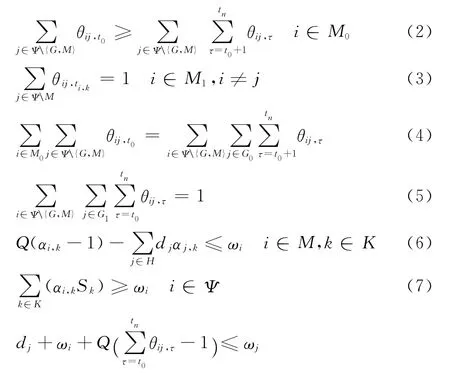
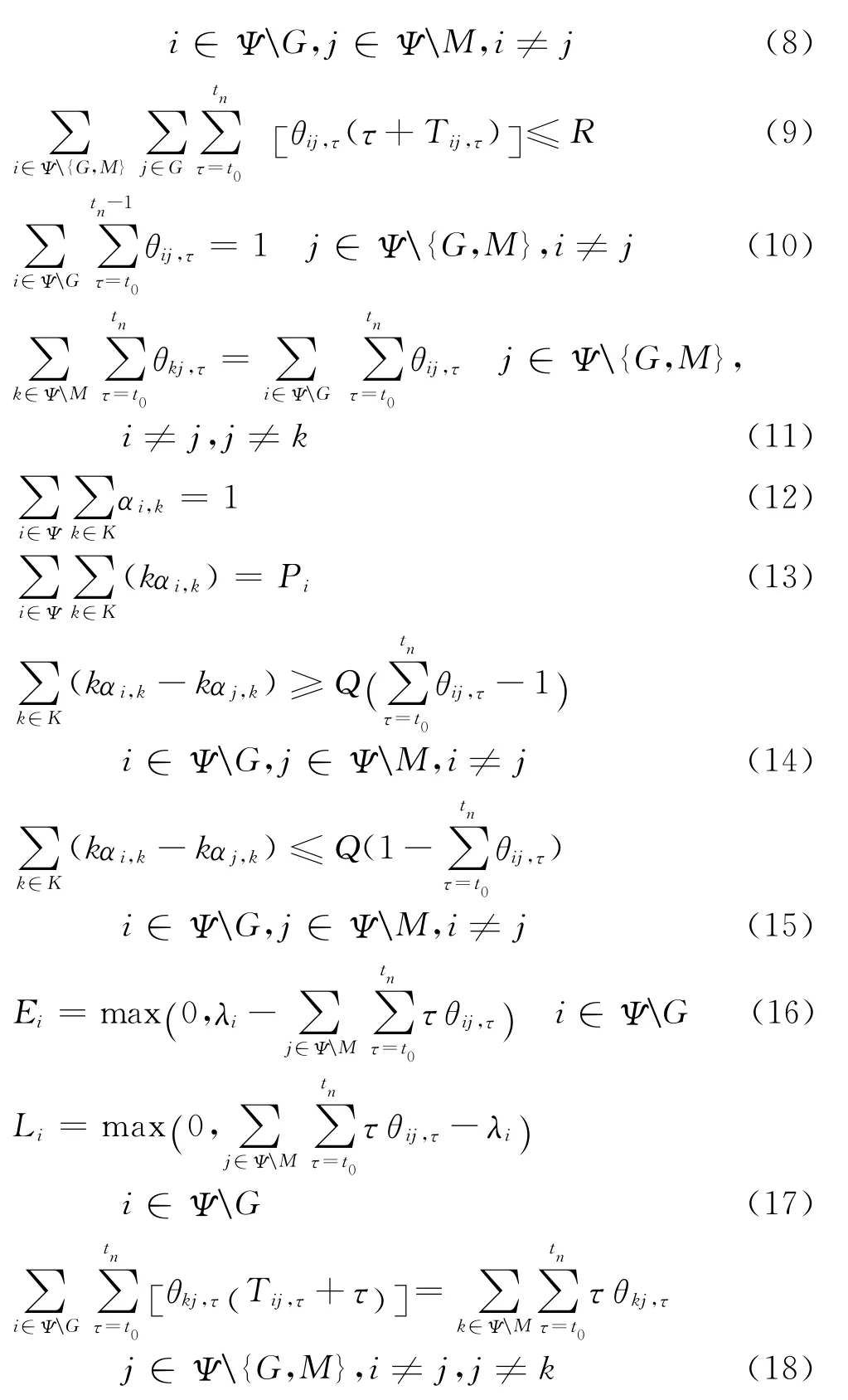
式中:Cf为车辆使用的固定成本;i,j为灾害点;M为所有车辆的出发节点;Ψ为所有灾害及救援节点;τ,t0,tn为时刻点;θij,τ为从τ 时刻开始救援车辆从灾害 点i到 达 灾 害 点j, θij,τ=;G为所有车辆的到达节点;Tij,τ为从τ时刻开始从灾害点i到达灾害点j的时间;We为过早到达灾害点的惩罚成本;Ei为在灾害点i的等待时间;Wl为延迟到达灾害点的惩罚成本;Li为延迟到达灾害点i的时间;M0为车辆的出发节点0;M1为车辆的出发节点1;G0为车辆的到达节点0;G1为车辆的到达节点1;Q为使用车辆的集合;αi,k为 灾 害 点i由 车 辆k实 施 救 援,αi,k=,k为车辆;d为灾j害点j的需求量;ωi为车辆离开灾害点i后的载重量;K为所有车辆总和;Sk为车辆k的承载能力;R为车辆路径总成本;Pi为第个灾害点被选上的概率;λi为期望到达灾害点i的时间。
式(1)是目标函数,用于最小化总成本,包括医疗救援车辆成本、路径成本和惩罚成本.之后的约束条件分为3类,第1类是关于医疗救援车辆的,由式(2)~(9)决定;第2类是关于灾害点特征的,由式(10)~(17)决定;第3类是关于路径特征的,由式(18)决定.式(2)和(3)表示医疗救援车辆在软时间窗的约束下从救援站或者其中一个灾害点开出;式(4)和(5)表示所有车辆都会回到救援站;式(6)~(8)表示车辆的承载能力;式(9)表示在救援计划完成前所有车辆都会返回到救援站;式(10)表示所有灾害点都会得到救助;式(11)和(12)表示每个灾害点仅由1部医疗救援车辆实施救助;式(13)决定了医疗救援车辆对任务分配的执行条件;式(14)和(15)表示2个相邻的灾害点由同一部救援车辆实施救助;式(16)和(17)用于计算由于违背软时间窗而带来的惩罚成本.方程式(13)决定路径的约束条件.
3 模型的求解
3.1 初始化
医疗救援路径通过一定的编码来分析,以便灾害点能够以一定的软时间窗顺序得到医疗救助,例如:有6个灾害点需要医疗救助,分别为D1,D2,D3,D4,D5,D6,如果令A0为救援站,而路径编码为(A0,D3,D5,D2,A0,D6,D1,D4,A0),可以看出,在软时间窗的约束下有2条路径可选,安排2部车辆分别实施救援,车辆1救援路径为:A0→D3→D5→D2→A0,车辆2救援路径为:A0→D6→D1→D4→A0,如果存在n部救援车辆,则每条染色体将有n条链接.在初始化阶段,通过以下3个步骤产生可行的初始化结果.①分配灾害点到每个链接上,实质是分组问题,灾害点将按与救援站的物理区域进行分组,目标是使总体的车辆行驶时间最小化.例如有2部车辆v1,v2用于医疗救援,救援站为A0,将每个灾害点i(xi,yi)按如下的原则进行分组:以救援站A0为圆心设定x,y轴,将x轴正值区的灾害点i(xi,yi)分配给v1,而x轴负值区的灾害点i(xi,yi)分配给v2,此时的灾害点i(xi,yi)与救援站的绝对距离为D(i,A0)=[(xi-xA0)2+(yi-yA0)2]-2.②对救援车辆的路径进行分配,利用Clarke等[9]的节约矩阵E(i,j)可以构建灾害点i,j与救援车辆的关联.首先假设在T0时刻2个灾害点分配在同一个路径链接上,再比较成本节约值E(i,j)=D(A0,i)+D(A0,j)-D(i,j),在保证车辆承载能力的前提下,成本节约值大的灾害点将得到保留.③利用近邻启发算法解决车辆路径问题,其原则是首先随机选择一个灾害点i,然后再选择另一个最近的灾害点j形成路径,直至所有的灾害点都覆盖到为止.
通过以上步骤可以实现问题的初始化,参照图1中的数据,可以得到具体初始化结果如图2所示.
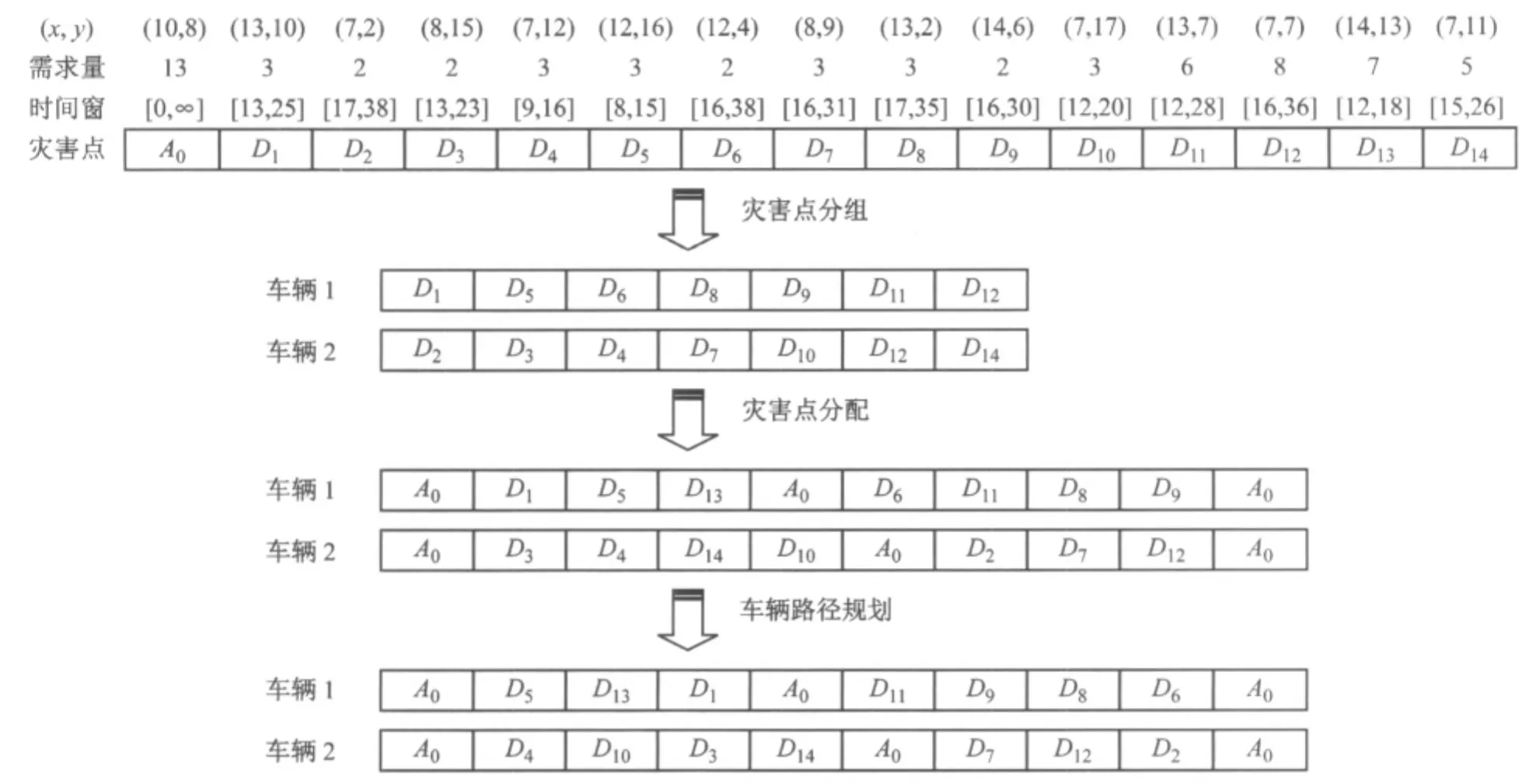
图2 混合遗传算法(HGA)初始化过程Fig.2 Initialization process of hybrid genetic algorithm
3.2 遗传迭代交换
此时引入最优搜索运算,对每2个灾害点进行遗传交换比较,如果产生的结果比初始状态好,则初始状态将被取代从而形成父代,直至所有的灾害点的遗传交换比较完成,最终产生新的父代。运算过程将消耗一定的时间,而迭代交换运算可以改进父代与子代之间的链接,需要通过以下5个步骤实现:①从父代中随机选择2个遗传基因;②交换2个遗传基因的位置从而形成子代;③互换2个遗传基因的相邻基因从而形成更多的子代;④评估所有子代并找到最好的一个;⑤如果最好的子代比父代好,则替换父代并重复步骤①,否则停止.图3展示这种迭代交换过程.
3.3 救援时间评价
这里需要最小化车辆的救援时间,由于每辆车的救援完成时间各不相同,所以必需以最晚完成救援的车辆作为救援结束的时刻。令Tva为车辆v所量,而Tvm(Xω) 为 车 辆vi所 耗 费 的最长时间,Xω代表第ω个染色体,则有Tva=,n为救援车辆的数max(Tv1a,Tv2a,…Tvna),式中:nv为所有救援车辆数目;t(i,j)为 从 灾 害 点i到j所 耗 费 时 间,为车辆行驶速度;nτ为在一条救援路径上灾害点的数量.

图3 混合遗传算法(HGA)迭代交换过程Fig.3 Iterative exchange process of hybrid genetic algorithm
3.4 染色体选择
这里需要选择一些染色体用于遗传运算,采用轮盘赌法选择健康的染色体,越健康的染色体被选上的机会越大,也就是说,染色体被选上的机率与其健康程度成正比。染色体选择通过以下步骤实现:①计算所有染色体的健康程度psize为被选染色体的规模;②计算每个染色体Xω被选择上的概率pω=[Ufit-Tvm(Xω)]/[Ufit(psize-1)],ω=1,2,…psize;③计算每个染色体Xω的累积概率Pω=∑ωi=1pi;④在范围(0,1]中产生任意的随机数λ,如果Pω≥λ>Pω-1,则染色体Xω将被选择.
3.5 遗传运算
遗传交叉算子可以找到更好的解决方案,而遗传变异算子可以扩展更大的搜索空间。下文用交叉算子、启发式变异和反转突变来产生改进的子代染色体。
3.5.1 顺序交叉
通过遗传交叉每次可产生2个子代染色体,可以通过以下步骤实现:①从第1组父代中随机选择1组基因子串;②复制该基因子串到原子串对应的位置,产生1组新的子串;③删除第2组父代中相应位置的基因,该位置的基因形成序列;④从左到右将原子串中空出位置按前步的序列顺序填满基因,从而形成一个新的子代;⑤通过交换2组父代的位置,重复步骤①~④的过程可产生另外一个子代.具体的遗传交叉过程如图4所示.
3.5.2 启发式变异
可以通过以下步骤实现:①从父代中随机选出3个遗传基因;②产生被选择基因所有可能的邻里排列,并生成所有的子代.具体的启发式变异过程如图5所示.
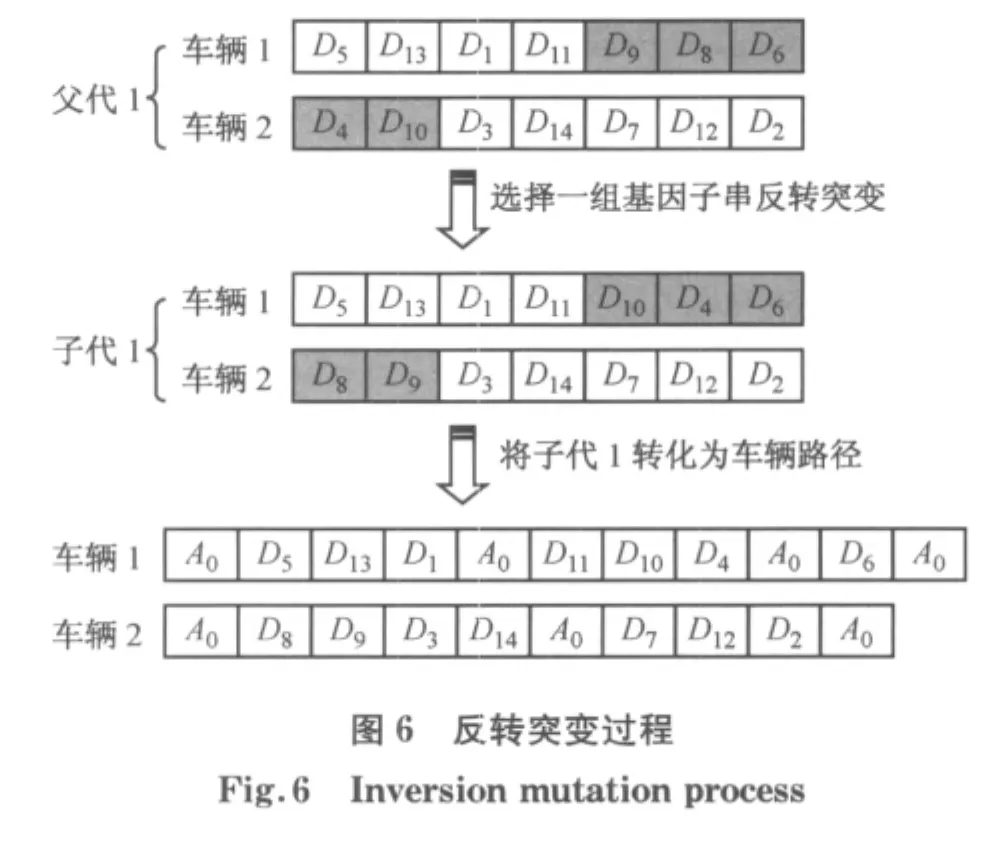
3.5.3 反转突变
逆算子作为一种变异运算仅仅用来增加样本的多样性,而不是加强样本的质量.具体的反转突变过程如图6.
4 数据仿真分析

2008年发生在我国四川汶川地区的里氏8.0级特大地震给灾区人民带来严重的生命和财产损失,此时需要各个医疗救援站积极响应,使医疗急救物资迅速运输到位.而各个救援站的车辆资源是有限的,需要合理调度,故此以非常规突发灾害事件为案例,依据前面的数学模型通过数据仿真分析HGA算法的有效性并与 Azi等[10]的精确算法(exact algorithm,EA)进行比较,说明其在处理带软时间窗的路径搜索问题方面的优势.EA算法可以精确到20个灾害点的情形,而灾害点大于20个时EA算法的计算时间会很长,在这里取某救援站所属区域有20个灾害点的情形进行比较分析,HGA算法采用MATLAB 7.1编程、Intel Core P8400/2.26GHz处理器 运 算,而 EA 算 法 利 用 AMPL Plus 1.5/CPLEX求解.在整个仿真测试过程中,假设有2部救援车辆用于医疗救助,各车辆的承载能力与灾害点的坐标及软时间窗都采用计算机随机生成,而HGA的初始数据也通过计算机随机生成,HGA迭代次数为200次,车辆行驶的时间间隔为2个单位,超出时间窗的惩罚成本We和Wl各取20个单位.

首先比较HGA和EA算法的总成本缺口率Cgap=(CHGA-CEA)/CEA×100%,其中CHGA,CEA分别为HGA和EA算法的总体成本消耗;运算时间的比率REH=TEA/THGA,其中TEA,THGA分别为EA 和HGA算法的运算时间,于是可以计算比较2种算法的总成本消耗和运算时间,由于灾害点小于4的比较意义不大,故随机采样数据计算从4个灾害点开始,如表1所示.
从表1可以看出,当灾害点的数量小于7个时,HGA和EA算法的总成本是相当的,而随着灾害点数量的增大,HGA和EA算法之间的总成本缺口发生变化,在20个灾害点时,总成本缺口达到了4.2%,在10个灾害点以内时,HGA和EA算法的运算时间差别不太大,而随着灾害点数量的增大,HGA算法体现出明显的时间优势,EA算法的运算时间将大量增加,而在20个灾害点时,EA算法运算所耗费的时间是HGA算法的133.3倍.
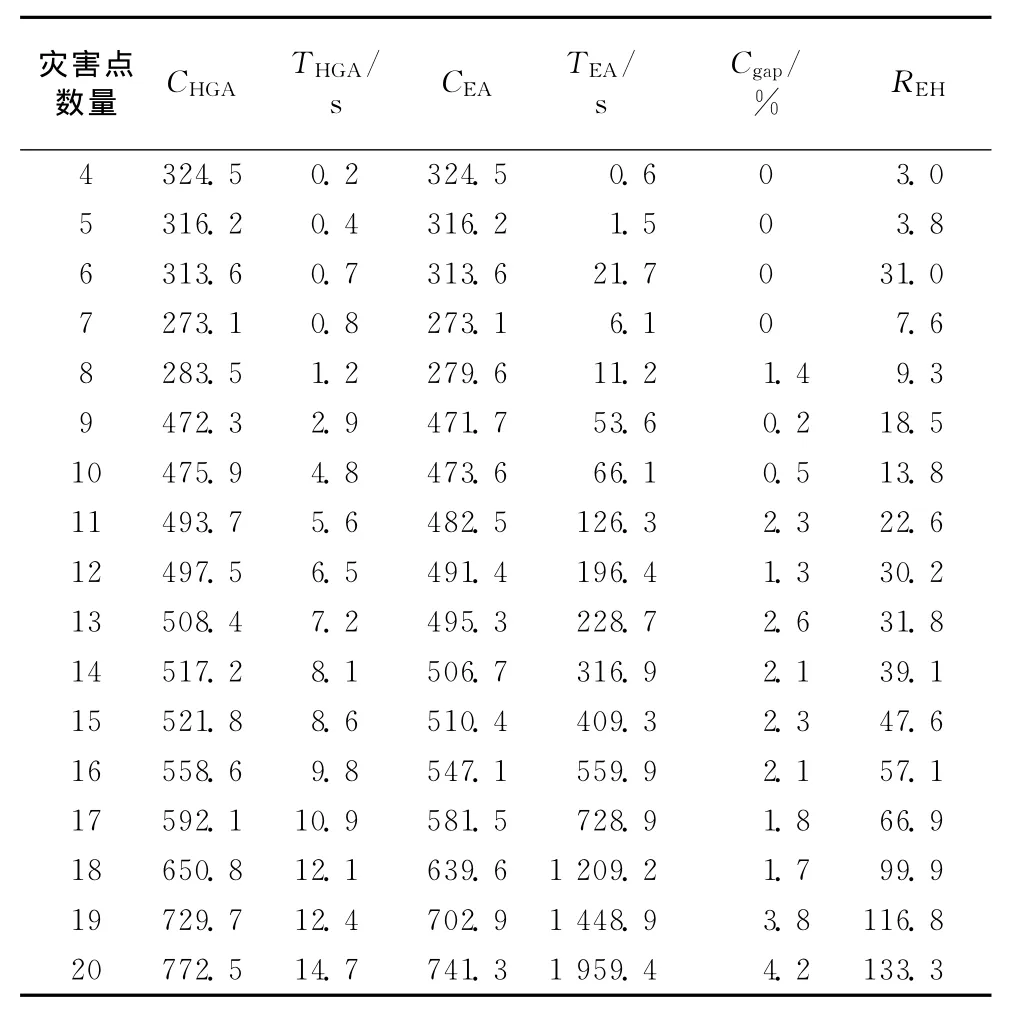
表1 HGA和EA算法的总成本及时间消耗比较Tab.1 Comparison of the total cost and time by HGA and EA algorithm
随着HGA算法迭代次数的增大医疗救援车辆的行驶时间进一步降低,从而优化总成本消耗和救援运输时间.下面分析HGA算法在20个灾害点的情况下,迭代运算200次,交叉率取0.4,突变率取0.2,随机取3对染色体进行遗传交叉,其中3个染色体作遗传变异和反转突变,于是每次迭代将产生18个子代,这样重复迭代200次可以得到如图7的结果.
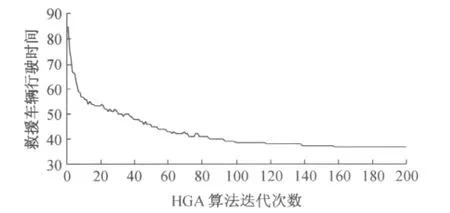
图7 HGA算法200次迭代收敛Fig.7 200 iterations converge of HGA algorithm
通过图7可以看出,随着HGA算法迭代次数的增加,救援车辆的行驶时间的优化趋于稳定,经过200次的迭代运算后,救援车辆的实际行驶时间从最初的85个单位缩减到37个单位.
5 结语
面对突发性非常规灾害事件,医疗急救物资的及时运输显得尤为重要,将有益于减少突发事件下的伤亡.针对软时间窗约束下的多辆医疗急救车辆的VRPTW问题建立了数学模型,得到最优总成本消耗下对各个灾害点救援的车辆行驶路径,同时有效缩短救援车辆的实际行驶时间.通过与EA算法进行数据仿真计算比较,结果表明HGA算法在总体成本消耗上与EA算法相当,但运算时间方面具有明显的优势.
[1] Desaulniers G,Lavigne J,Soumis F.Multi-depot vehicle scheduling problems with time windows and waiting costs[J].European Journal of Operational Research, 1998, 111(3):479.
[2] Qureshi A G,Taniguchi E,Yamada T.An exact solution approach for vehicle routing and scheduling problems with soft time windows[J].Transportation Research Part E:Logistics and Transportation Review,2009,45(6):960.
[3] Ghoseiri K,Ghannadpour S F.Multi-objective vehicle routing problem with time windows using goal programming and genetic algorithm[J].Applied Soft Computing,2010,10(4):1096.
[4] Taillard E D,Laporte G,Gendreau M.Vehicle routing with multiple use of vehicles[J].Journal of the Operational Research Society,1996,47:1065.
[5] Campbell A M,Savelsbergh M.Efficient insertion heuristics for vehicle routing and scheduling problems[J].Transportation Science,2004,38:369.
[6] Marinakis Y,Marinaki M,Dounias G.A hybrid particle swarm optimization algorithm for the vehicle routing problem[J].Engineering Applications of Artificial Intelligence,2010,23(4):463.
[7] Tan K C,Lee L H,Ou K.Artificial intelligence heuristics in solving vehicle routing problems with time window constraints[J].Engineering Applications of Artificial Intelligence,2001,14(6):825.
[8] Park Y B.A hybrid genetic algorithm for the vehicle scheduling problem with due times and time deadlines[J].International Journal of Production Economics,2001,73(2):175.
[9] Clarke G,Wright J W.Scheduling of vehicles from a central depot to a number of delivery points[J].Operations Research,1964,12:568.
[10] Azi N,Gendreau M,Potvin J Y.An exact algorithm for a vehicle routing problem with time windows and multiple use of vehicles[J].European Journal of Operational Research,2010,202(3):756.
——基于人力资本传递机制
——基于反向社会化理论的实证研究
——基于子女数量基本确定的情形

