双离合器自动变速器起步的智能控制策略
吴光强,司建玉
(1.同济大学 汽车学院,上海201804;2.东京大学 生产技术研究所,东京153-8505)
双离合器自动变速器(dual clutch transmission,DCT)起步控制技术就是指起步过程中离合器的控制技术[1-3].根据DCT的结构特点,其起步既可以使用单离合器也可以使用双离合器,目前对DCT起步过程的研究主要集中在单离合器起步,而双离合器起步的研究相对较少.其中文献[4-5]把模糊控制理论应用到了单离合器起步的控制中,制定了车辆起步时离合器接合速度的模糊控制规则,仿真验证的结果表明控制效果较好.国内外学者对基于智能控制技术的离合器起步控制进行了较为深入的研究,但也存在诸多不足,如未综合考虑驾驶员的起步意图、路况、车况及离合器的接合状态对起步的影响.
本文在综合考虑了驾驶员的起步意图、车辆负载、路面坡度及离合器接合状态的基础上研究了双离合器协同起步过程,提出了基于模糊控制和神经网络的智能控制策略,以DCT起步过程中的起步时间、滑摩功及冲击度为评价指标,利用快速起步、慢速起步及驾驶员意图多变的起步工况对所制定智能控制策略的合理性进行了验证.
1 DCT起步过程建模
1.1 DCT传动系统模型
DCT的挡位按照奇数和偶数分为2组,奇数挡位与离合器1相连,偶数挡位与离合器2相连.通过预先接合同步器实现动力换挡过程[6-7].离合器1,2的接合与分离根据作动方式的不同,通常分为液作动和电作动.图1为DCT传动系统的结构示意.

图1 双离合器自动变速器传动系统结构示意Fig.1 Dual clutch transmission driving system schematic
1.2 双离合器起步动力学模型
DCT双离合器起步过程可简化为一个离散化的系统模型,如图2所示.图中,Te为发动机转矩;ωe为发动机的转速;Tc1e,Tc2e分别为离合器1和2对发动机的反作用转矩;Tec1,Tec2分别为发动机传递给离合器1和2的转矩;ωc1,ωc2分别为离合器1和2从动部分的转速;Toc1,Toc2分别为变速器输出轴对离合器1和2的反作用转矩;Tc1o,Tc2o分别为离合器1和2传递给变速器输出轴的转矩;ωo为输出轴转速;Tf为转换到变速器输出轴上的阻力矩.
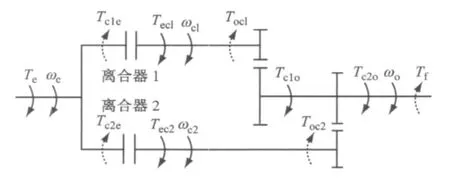
图2 双离合器起步的动力学模型Fig.2 Dual clutch launching drive train model
双离合器起步过程的动力学方程为Te-Tc1e-Tc2e-beωe=Iedωe/dt,Tec1-Toc1-bc1ωc1=Ic1·dωc1/dt,Tec2-Toc2-bc2ωc2=Ic2dωc2/dt,Tc1o+Tc2o-Tf-boωo=Iodωo/dt,其中:ωc1=i1ωo,ωc2=i2ωo,Tec1=ZμF1R,Tec1=ZμF2R。起步完成后稳定行驶阶段的动力学方程为:Te-Toc1-bc1ωc1=(Ie+Ic)dωe/dt,ωc1=ωe,式中:be,bc1,bc2及bo为阻尼;Ie,Ic1,Ic2,Io,Ic分别为发动机及离合器主动部分、离合器1从动部分、离合器2从动部分、变速器输出轴到车轮的转动惯量及起步完成后稳定行驶时等效到离合器1的转动惯量;t为时间;i1,i2分别为变速器1和2挡速比;Z为离合器摩擦面个数;μ为摩擦因数;F1,F2分别为作用在离合器1和2压盘上的等效正压力;R为离合器等效半径.
1.3 起步性能评价指标
对车辆起步过程进行定量评价时的指标主要有冲击度和滑摩功[8].
1.3.1 冲击度
冲击度是评价离合器接合过程平稳程度的指标,定义为车辆纵向加速度的变化率,表达式为j=da/dt=d2v/dt2,式中:j为冲击度,最大推荐值10 m·s-3;a为车辆纵向加速度;v为车辆行驶速度.
1.3.2 滑摩功
滑摩功是评价离合器使用寿命的指标,是离合器摩擦片间滑动时摩擦力做功的大小,表达式为,式中:W为滑摩功;Tc为离合器传递的转矩;ωc为离合器从动部分的转速;t0为离合器摩擦面开始接触的时间起点;t1为从离合器摩擦面开始接触(Tc=0)起直到Tc逐渐增大到能够克服汽车行驶阻力矩Tf所经历的时间;t2为从Tc大于Tf起直到ωc从零逐渐增大到与ωe相等所经历的时间.
2 起步控制系统描述
模糊控制技术可以利用人的知识和经验达到模仿人的思维来控制汽车起步的目的,而且对难以建立数学模型、非线性和大滞后的控制对象具有很好的适应性,非常适用于离合器的起步控制.而神经网络又具有并行计算、分布式信息存储、容错能力强及具备自学习功能等优点,所以基于模糊控制和神经网络理论并结合DCT车辆起步控制的特点设计了DCT起步的智能控制系统,如图3所示.主要由驾驶员意图的模糊推理系统、离合器接合速度的模糊推理系统及离合器滑差率神经网络控制系统组成.图中,ωc为离合器从动盘转速;Fd为离合器输出的驱动力;vs为车辆行驶速度;vc为离合器接合速度;ice为离合器转速比;μc为离合器滑差率阈值;L为车辆负载;I为起步意图;i为路面坡度;Δne为发动机实际转速与目标转速差;α为油门开度.
起步控制系统首先根据α及˙α由模糊推理系统推理出驾驶员的起步意图,然后根据I和Δne和ice推理出vc,同时,由起步意图1,L及i经离合器滑差率神经网络控制系统得到μc,最后由vc和μc共同控制离合器的起步过程.
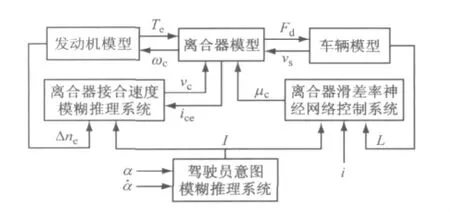
图3 起步控制系统简图Fig.3 Launching control schematic
3 起步的智能控制策略制定
基于优秀驾驶员的操作经验制定了驾驶员意图的模糊控制规则,根据α和Δα实时识别出I.同时,以I,L及i为输入参数,基于人工神经网络理论设计了双离合器起步的神经网络控制系统.
3.1 模糊规则制定
3.1.1 驾驶员意图的模糊规则制定
根据α和˙α推理出I.驾驶员意图的模糊控制系统各变量的语言集和基本论域如下:α为{非常小(VS)、小(S)、中等(M)、大(B)、非常大(VB)},{0,1};˙α 为 {负大(NB)、负中(NM)、负小(NB)、零(ZE)、正小(PS)、正中(PM)、正大(PB)},{-6,6};I为{非常慢(VS)、慢(S),中等(M)、急(B)、非常急(VB)},{0,1}.
基于优秀驾驶员的操作经验,制定的驾驶员意图的模糊控制规则如表1所示,根据控制规则综合判断后给出驾驶员的驾驶意图,并作为输入参数用于起步自适应控制的推理.
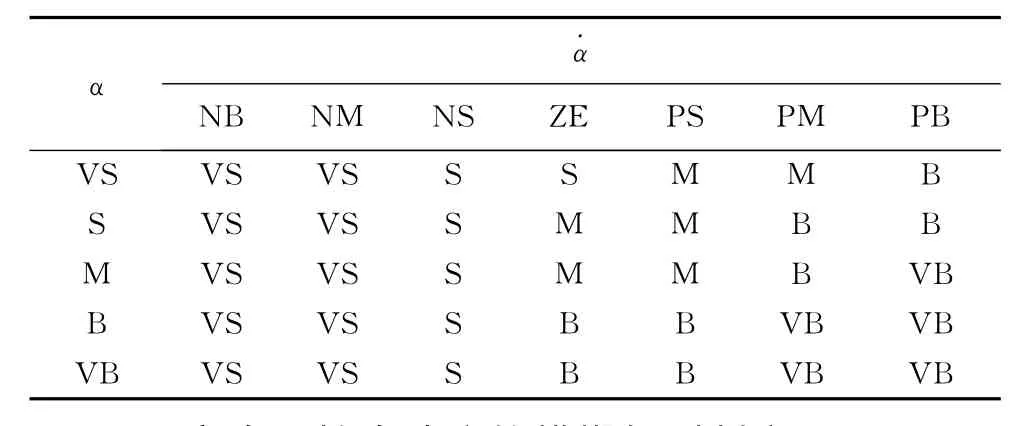
表1 驾驶员意图模糊规则Tab.1 Driver intention fuzzy rules
3.1.2 离合器接合速度的模糊规则制定
车辆起步过程中,离合器的接合速度直接影响起步性能,包括起步时间、冲击度及滑摩功的大小[9].双离合器协同起步过程中,对离合器接合速度的控制还需要考虑2个离合器输出力矩的分配问题,这里以2个离合器输出到车轮扭矩相等的原则进行扭矩的分配,同时,还必须保证离合器的接合速度能够反映驾驶员的驾驶意图.另外,离合器接合速度还要考虑发动机转速的变化情况,如果发动机接合过程中转速下降较快则应该减慢接合速度,反之则加快离合器接合速度,这里对发动机转速的控制采用的方法是由油门开度制定发动机目标转速,并通过控制离合器的接合速度来减小实际转速与目标转速的偏差.同时,离合器主从动盘的转速差也应该考虑在接合速度的控制中,这里以离合器主从动盘的转速差Δnc与发动机转速ne的比值ice来表征离合器的接合状态并对输入参数进行模糊化处理.
设由 Δne和ice决定vc.Δne,ice及vc各模糊语言集合 基 本 论 域 如 下:Δne为 {负(N)、零(ZE)、正(P)},{-1,1};ice为 {非 常 小(VS)、小(S)、中(M)、大(B)、非常大(VB)},{0,1};vc为{慢(S)、较慢(LS)、中等(M)、较快(LB)、快(VB)},{0,10}.
离合器接合速度的模糊控制规则如表2所示.

表2 离合器接合速度模糊规则Tab.2 Clutch engaging speed fuzzy rules
3.1.3 模糊控制变量隶属度函数的选择
根据模糊控制变量及其特点,在综合考虑了各隶属函数适用情况的基础上,选用了常用的高斯型隶属度函数.模糊变量隶属度函数如图4所示.
3.2 离合器滑差率神经网络控制模型
3.2.1 神经网络模型及参数
双离合器协同起步时2个离合器的接合与分离时序是控制时需要解决的关键问题.由于需要综合考虑驾驶员意图、车辆负载及路面坡度等人-车-路环境的影响,传统方法建立的模型只能得到有限个精确的数据值,无法自适应各因素不断变化的特性,而神经网络模型恰恰能弥补传统方法的不足.这里以离合器1主从动盘的转速差与主动盘转速的比值(定义为离合器1滑差率)为控制目标,以I,L及i为输入参数,以离合器1滑差率阈值为控制参数,设计了4层神经网络模型.离合器滑差率阈值神经网络模型如图5.图中,j,k,l,m,n为神经网络节点编号;Wij为节点i,j间的权值;Wjk为节点j,k间的权值;Wkl为节点k,l间的权值.
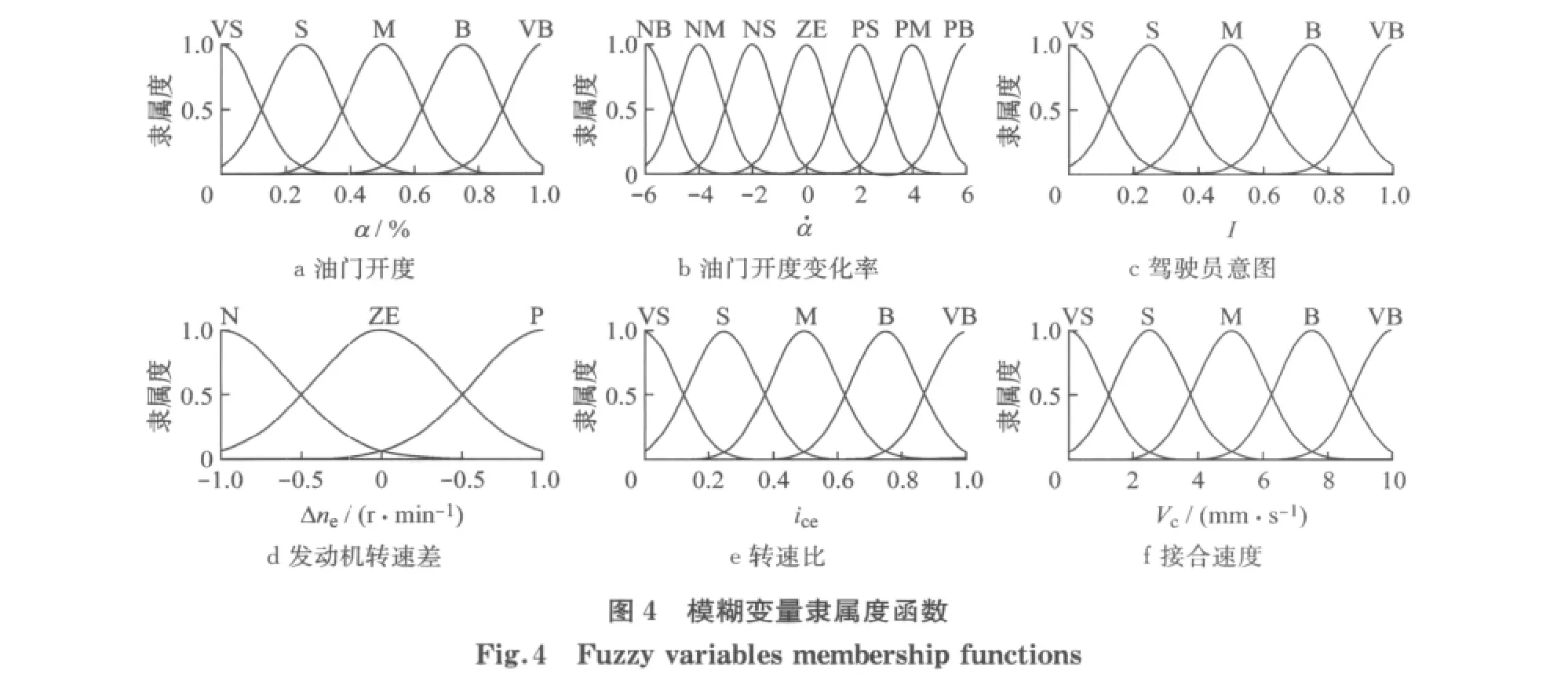

图5 神经网络模型示意Fig.5 Neural networ k schematic
第1层为输入层,采用I,L及i为输入,该层的结点数为3;第2,3层为隐含层,该层的结点数分别为9,6;第4层为输出层,采用离合器1滑差率阈值为输出.神经网络模型的参数如表3所示.

表3 神经网络模型参数Tab.3 Neural network model parameters
3.2.2 神经网络的训练
基于表3的神经网络类型及具体参数构造神经网络模型,由于BP(back propagation)神经网络学习速度慢,而且易于落入局部极小,所以这里采用了加入动量项和全局误差累积计算的方法改进了其学习速度慢的不足之处[10-11].训练时,根据已有的仿真及测试结果以快速、中速、慢速起步意图、车辆轻、中、重载,路面坡度0,5,10,15,20°及离合器滑差率阈值0.05,0.10,0.15,0.20的相应组合作为训练样本训练得到满足泛化要求的神经网络模型.
4 仿真结果及分析
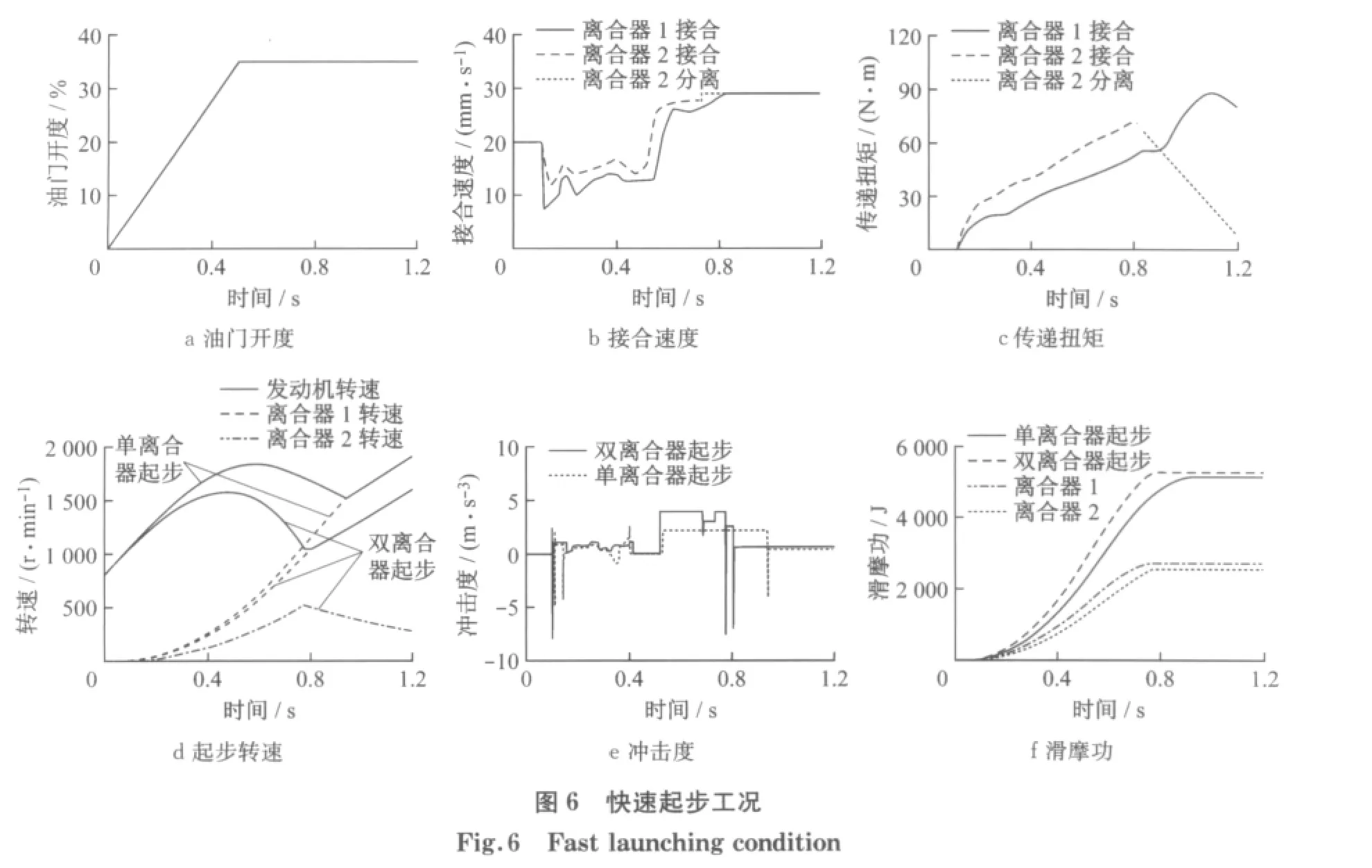
以DCT起步过程中的起步时间、滑摩功及冲击度为评价指标,利用快速起步、慢速起步及驾驶员意图多变的起步工况并以车辆轻载情况为例通过仿真对所制定的起步智能控制策略进行了验证.仿真结果如图6~8所示.
从图6可以看出,对于快速起步工况,单离合器起步时间约为0.950 s,双离合器协同起步时间缩短为约0.807 s;但滑摩功由单离合器起步的约5 148 J增加为双离合器协同起步的约5 279 J,双离合器协同起步中离合器1,2的滑摩功分别为2 721,2 558 J;而双离合器冲击度峰值较单离合器大,但都小于冲击度的推荐值(10 m·s-3).就离合器接合过程而言,起步开始时,离合器1,2以20 mm·s-1的速度快速接合以消除离合器主从动盘的间隙,之后双离合器的接合速度由模糊控制系统决定.离合器1从起步开始按照预先的控制规则要求接合,而离合器2根据离合器滑差率阈值(此工况下为4.42%)到0.777 s时开始分离,离合器1主从动盘在0.807 s接合速度达到同步,离合器1以30 mm·s-1的接合速度完成剩余行程.同时,为了减少离合器2在分离时候的滑摩功,离合器2的分离速度比接合速度快,且双离合器协同起步时离合器接合速度的模糊控制对双离合器接合速度的控制比较平稳.
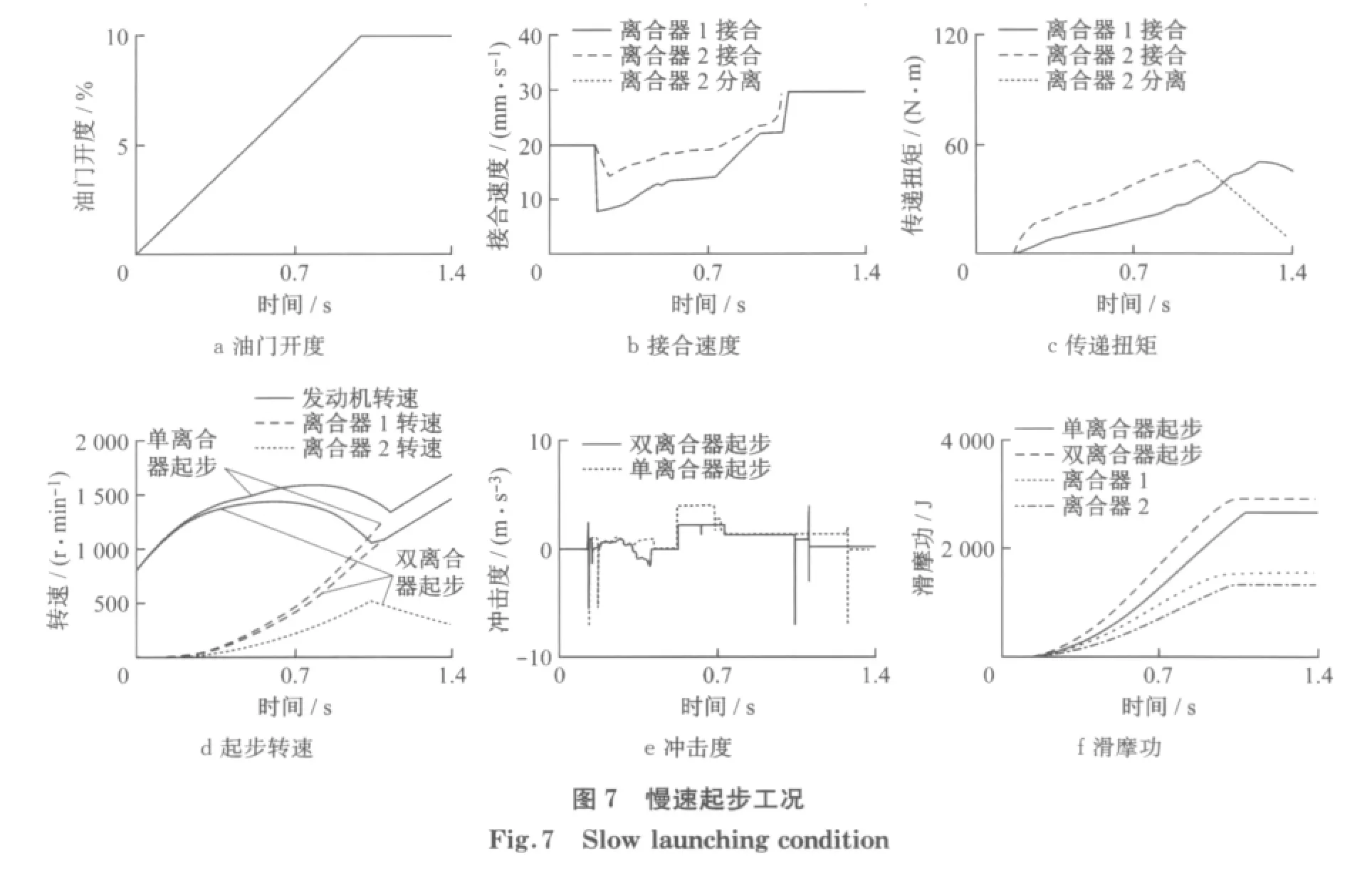
对于图7的慢速起步工况,起步开始时,为消除离合器主从动盘的间隙,离合器1,2先以20 mm·s-1的速度快速接合,此后双离合器的接合速度就由模糊控制系统决定.离合器1从起步开始按照预先的控制规则要求接合,而离合器2根据离合器滑差率阈值(此工况下为6.31%)到0.95 s时开始分离,离合器1主从动盘在1.13 s接合速度达到同步,此后离合器1以30 mm·s-1的接合速度完成剩余行程.此工况下离合器2的分离速度比接合速度快,以便减少离合器2在分离时候的滑摩功.就起步时间而言,单离合器起步和双离合器协同起步的起步时间都大于1 s,较快速起步工况有了明显的延长,而双离合器协同起步略快于单离合器起步.同时,双离合器协同起步的滑摩功也略高于单离合器起步.无论是单离合器起步还是双离合器起步冲击度都小于推荐值(10 m·s-3).
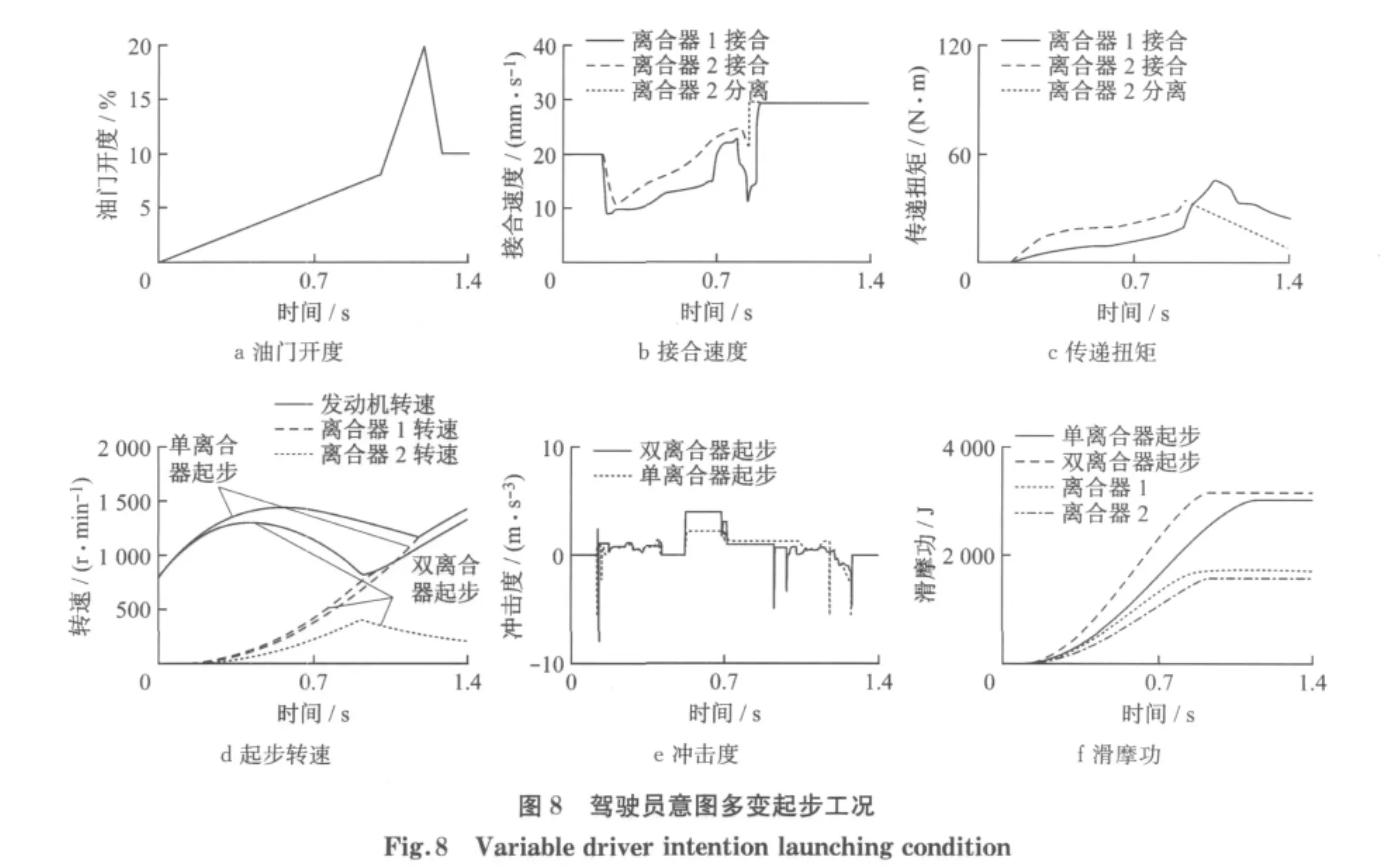
图8是驾驶员意图多变起步工况,此工况下,离合器1,2先以20 mm·s-1的速度快速接合以消除离合器主从动盘的间隙,此后双离合器的接合速度由模糊控制系统决定.整个接合分离过程中,根据制定的离合器接合速度的模糊规则完成了双离合器的控制.离合器1从起步开始按照预先的控制规则要求接合,而离合器2根据离合器滑差率阈值(此工况下为5.23%)到0.925 s时开始分离,离合器1主从动盘在0.984 s接合速度达到同步,此后离合器1以30 mm·s-1的接合速度完成剩余行程.此工况下离合器2的分离速度比接合速度快,以便减少离合器2在分离时候的滑摩功.对于起步时间而言,单离合器起步和双离合器起步较快速起步工况都有所延长,并且起步过程中冲击度也有了较为明显的变化,但也都小于推荐值.双离合器协同参与的起步过程使得单个离合器的滑摩功较单离合器起步明显减少,有利于延长离合器的使用寿命.但双离合器协同起步的控制策略较单离合器起步复杂,增加了控制系统实现的难度.
5 结论
(1)参考优秀驾驶员的操作经验,制定了驾驶员意图的模糊控制规则.以驾驶员意图、车辆负载及路面坡度为输入参数,以离合器滑差率阈值为控制参数,设计实现了双离合器滑摩过程控制的神经网络模型.
(2)以DCT起步过程中的起步时间、滑摩功及冲击度为评价指标,对快速起步、慢速起步、坡道起步及驾驶员意图多变的起步工况进行了仿真验证,并与单离合器起步工况进行了对比分析,验证与对比结果表明所制定的双离合器协同起步的智能控制策略对不同工况具有自适应性.
(3)典型工况的仿真结果表明,双离合器协同参与的起步过程使单个离合器的滑摩功较单离合器起步明显减少,有利于延长离合器的使用寿命.同时,双离合器协同起步的起步时间较单离合器起步也有较明显的缩短,有利于车辆的快速起步.然而,双离合器协同起步的控制策略较单离合器起步复杂,以致增加了控制系统实现的难度.
[1] Goetz M,Levesley M C,Crolla D A.Integrated powertrain control of gearshifts on twin clutch transmissions[C]∥2004 SAE World Congress Detriot.Detriot:SAE,2004:SAE paper 2004-01-1637.
[2] 吴光强,杨伟斌,秦大同.双离合器式自动变速器控制系统的关键技术[J].机械工程学报,2007,43(2):13.WU Guangqiang,YANG Weibin,QIN Datong.Key technique of dual clutch transmission control system[J].Chinese Journal of Mechanical Engineering,2007,43(2):13.
[3] ZHANG Y,CHEN X,JIANG H,et al.Dynamic modeling and simulation of a dual-clutch automated lay-shaft transmission[J].Journal of Mechanical Design,Transactions of the ASME,2005,127(2):302.
[4] TANG Xianqing,HOU Chaozhen,CHEN Yunchuang.Study of controlling clutch engagement for AMT based on fuzzy logic[J].Journal of Beijing Institute of Technology,2002,1l(1):45.
[5] 程秀生,冯巍,陆中华,等.湿式双离合器自动变速器起步控制[J].农业机械学报,2010,14(1):18.CHENG Xiusheng,FENG Wei,LU Zhonghua,et al.Starting control based on wet dual clutch transmission[J].Transactions of the Chinese Society for Agricultural Machinery,2010,14(1):18.
[6] Bernd Matthes.Dual clutch transmissions-lessons learned and future potential[J].2005 SAE World Congress.Detriot:SAE,2005:SAE paper 2005-01-1021.
[7] Zhang Y,Kulkarni M,Marine M,et al.Launch and shift dynamics of dual-clutch transmission vehicles [C ] ∥Proceedings of the International Conference on Mechanical Transmissions 2006,Beijing:Science Press,2006:400-406.
[8] 葛安林.车辆自动变速理论与设计[M].北京:机械工业出版社,1993.GE Anlin.Theory and design of automatic transmission[M].Beijing:China Machine Press,1993.
[9] LIU Haiou,CHEN Huiyan,DING Huarong,et al.Adaptive clutch engaging Process control for automatic mechanical transmission[J].Journal of Beijing Institute of Technology,2005,14(2):170.
[10] Haykin S.Neural networks and learning machines [M].Beijing:China Machine Press,2009.
[11] Ripley B D.Pattern recognition neural networks [M].Beijing:Posts &Telecom Press,2009.

