基于鼓形面的车门玻璃及导轨设计
高大威,高云凯,周晓燕,刘海立
(1.同济大学 汽车学院,上海201804;2.上海理工大学 机械工程学院,上海200093)
长期以来,汽车造型设计与车身设计中遇到的一个难点就是车门玻璃的型面设计.现代汽车车身外型设计越来越强调流线型,为了满足不断提高的要求,越来越多的乘用车车门采用双曲面玻璃,熟悉的车型有中华轿车、PASSAT B5等.双曲面玻璃不仅在升降方向上曲率大于零,而且在车身长度方向上曲率也大于零,其升降运动是一种上下转动与侧向滑移的合成运动.这种复杂的合成运动不仅对玻璃曲面提出了更高的要求,而且对玻璃引导系统的布置同样提出了非常高的要求.
近年来,虽然双曲面玻璃已经被应用在国内外开发的许多车型上,但成熟、公开的资料基本没有,并且存在很多问题,工程设计和制造质量不高.同济大学的高云凯教授等[1]、同济同捷科技股份有限公司的雷雨成教授等[2]采用圆环面方法拟合双曲面玻璃,并且利用UG等软件实现了圆环面玻璃的几何设计和运动分析,但是车门玻璃运动时的最大偏差为2.8~3.5 mm,偏差较大.北美通用的Lin C L[3-4]利用车门CAE模型进行了钢丝绳式玻璃引导系统的虚拟试验设计研究,同时还研究了车门玻璃在升降运动中的鲁棒性问题.福特公司的K.Singh等[5]借助CAE(computer aided engineering)分析方法研究了普通车门玻璃在升降运动过程中的偏差以及密封条变形.
笔者结合上海某汽车设计公司的一款车型,针对左侧后门玻璃进行了玻璃曲面以及玻璃引导系统的布置设计.首先,利用线元几何构造运动方程并结合K-Local-RANSAC算法根据车身点云数据得到鼓形面,以鼓形面拟合双曲面玻璃;同时,按照鼓形线原理,使用比例函数的方法拟合玻璃升降导轨曲线;最后,通过运动偏差分析,最大位置偏差小于0.6 mm,完全符合工程偏差要求.证明玻璃曲面拟合及其导轨设计的正确性与准确性.
1 设计理论
目前对于双曲面玻璃的拟合方法使用较多的是将柱面的变形曲面即圆环面作为玻璃型面[6],但是在实际工程的运用中存在以下2个问题:①玻璃运动不够稳定;②造型面与圆环面偏差过大,难以符合工程要求.
实际上,车门玻璃的外形从侧视图看,其前后边界线应是平行曲线;从俯视图看,玻璃外形由最大截面向前后是缓慢往内收的,因此,玻璃半径也应从最大截面处的半径往前后逐步减小以适应车身造型规律,所以车门的玻璃表面应为鼓形表面[7].鼓形面是以一条直线为轴线,同时沿轴线方向存在半径差的一种双曲面.车身造型点云包含多种不同部位的特征曲线与隐含信息,为了能够准确拟合出车门玻璃所在的鼓形面,使用VC++语言,采用线元几何构造运动方程并结合K-Local-RANSAC算法拟合鼓形面.首先将三维空间中的点投影到线元空间中构建线性丛,而后利用线性丛表示曲面,通过拟合运动方程得到旋转运动的特征参数,从而计算出旋转轴所在位置.此方法计算速度快,并且无须得到精确的曲面法矢就能够快速识别曲面并提取旋转面的一般特征[8].所得鼓形面如图1所示.
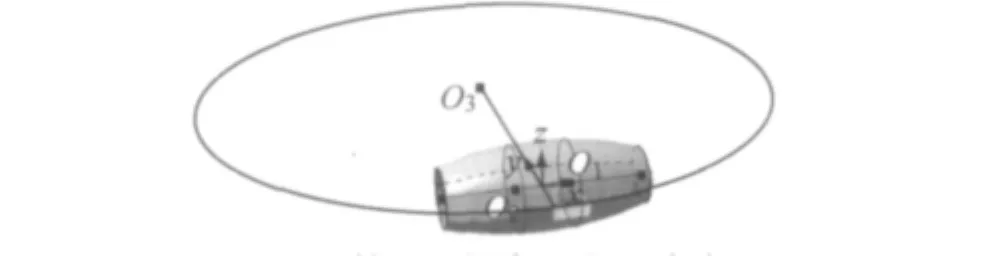
图1 鼓形面拟合双曲面玻璃Fig.1 The drum surface fitting the dualcurvature glass
建立局部坐标系(图1),以鼓形面的旋转轴O1O2为x轴;在车门下窗台线附件用过x轴的平面截取鼓形面,拟合大圆O3,定义大圆径向且与O1O2垂直的半径为y轴.设大圆半径为r,大圆圆心到原点的距离即O3O距离为h,且该距离在旋转过程中是不变的(图2).那么,鼓形面满足下列公式:初始位置,大 圆为O1,O2点之间的距离,所以,鼓形面的方程可以表示为
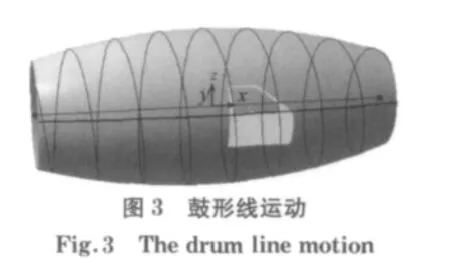
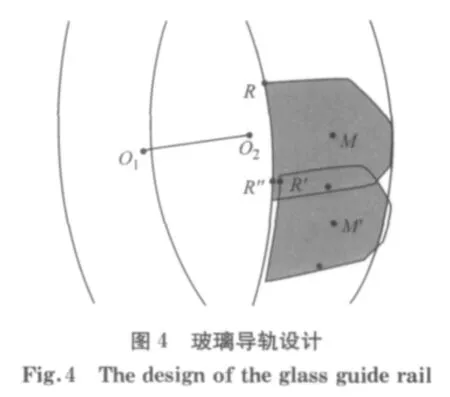
另外由于车门玻璃与Oxz平面及Oyz平面均有一定的角度,因此可以知道车门玻璃的运动实际上是一种鼓形线运动,如图3所示.根据鼓形线的运动理论可知:理想情况下,即玻璃曲面不存在运动偏差时,玻璃曲面在下降过程中R点一定经过R″点.但实际运动过程中,由于角度的存在,车门玻璃由初始位置上的R点先绕轴线O1O2旋转到R′点,然后再沿轴线O1O2方向偏移到R″点,如图4所示.那么玻璃质心M点沿同样的鼓形线运动时,点M的运动轨迹即为玻璃导轨的导线.
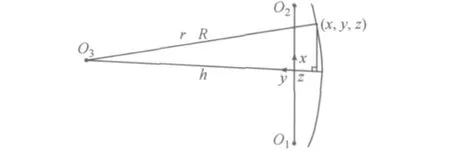
图2 鼓形面拟合参数Fig.2 The fitting parameter of the drum surface
2 设计方法
按照拟合鼓形面的方法,采用上海某设计公司设计的一款A级车[1],以左侧后门玻璃为例(图5),已知条件如下:①车身造型点云数据;②车门玻璃前后边界线、上下窗台线等.
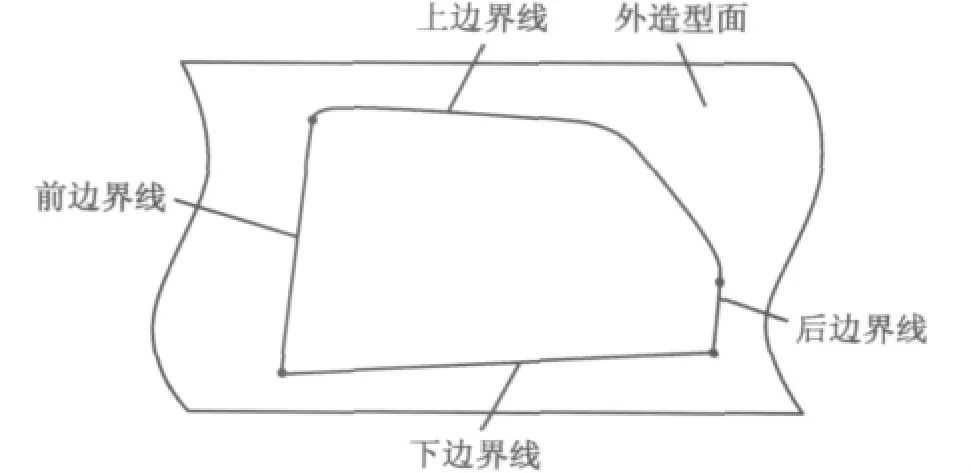
图5 玻璃曲面设计已知条件Fig.5 The glass surface design condition
根据车门玻璃边线得到鼓形面车门玻璃.从侧视图看,玻璃曲面的前后边界线是一对平行曲线,如图6所示.从俯视图看,玻璃曲面外形由车身最大截面向后是缓慢往内收的,也就是前文所说的鼓形面,如图7所示.图中,B柱和C柱分别指玻璃的前端和后端.

图6 玻璃曲面前后边界线Oyz平面投影Fig.6 The front and rear boundary of the glass surface on Oyz flat

图7 左侧后门玻璃曲面俯视截面Fig.7 The glass surface section of the left-rear door
同时根据按照鼓形线原理进行玻璃导轨导线的拟合,设计步骤如下:①将O1O2作为玻璃曲面的旋转轴线,如图8所示;②选取玻璃边界上的2个点R和T.过R点作垂直轴线的平面,将T投影到此平面得到T′;测量∠RO1T′角度α,TT′距离L,见图8;③根据鼓形线原理可知,玻璃上每一个点的旋转与平移存在比例函数关系:④α/Δα=L/ΔL.那么,将玻璃质心M点每旋转Δα角度,就沿轴线偏移ΔL距离.为了得到光滑的拟合曲线,取Δα=0.1°,即可得到玻璃曲面下降过程中每旋转0.1°时质心点的位置.根据这些点即可拟合出一条曲线,即可得到玻璃导轨的导线.⑤将玻璃曲面沿所得到的导轨曲线运动,测量玻璃下降到不同位置时玻璃边界与导槽中心线之间的偏差.
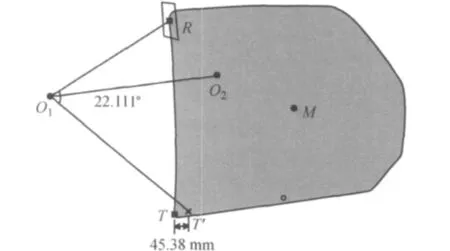
图8 玻璃导轨设计应用Fig.8 The glass guide rail design application
3 运动偏差分析
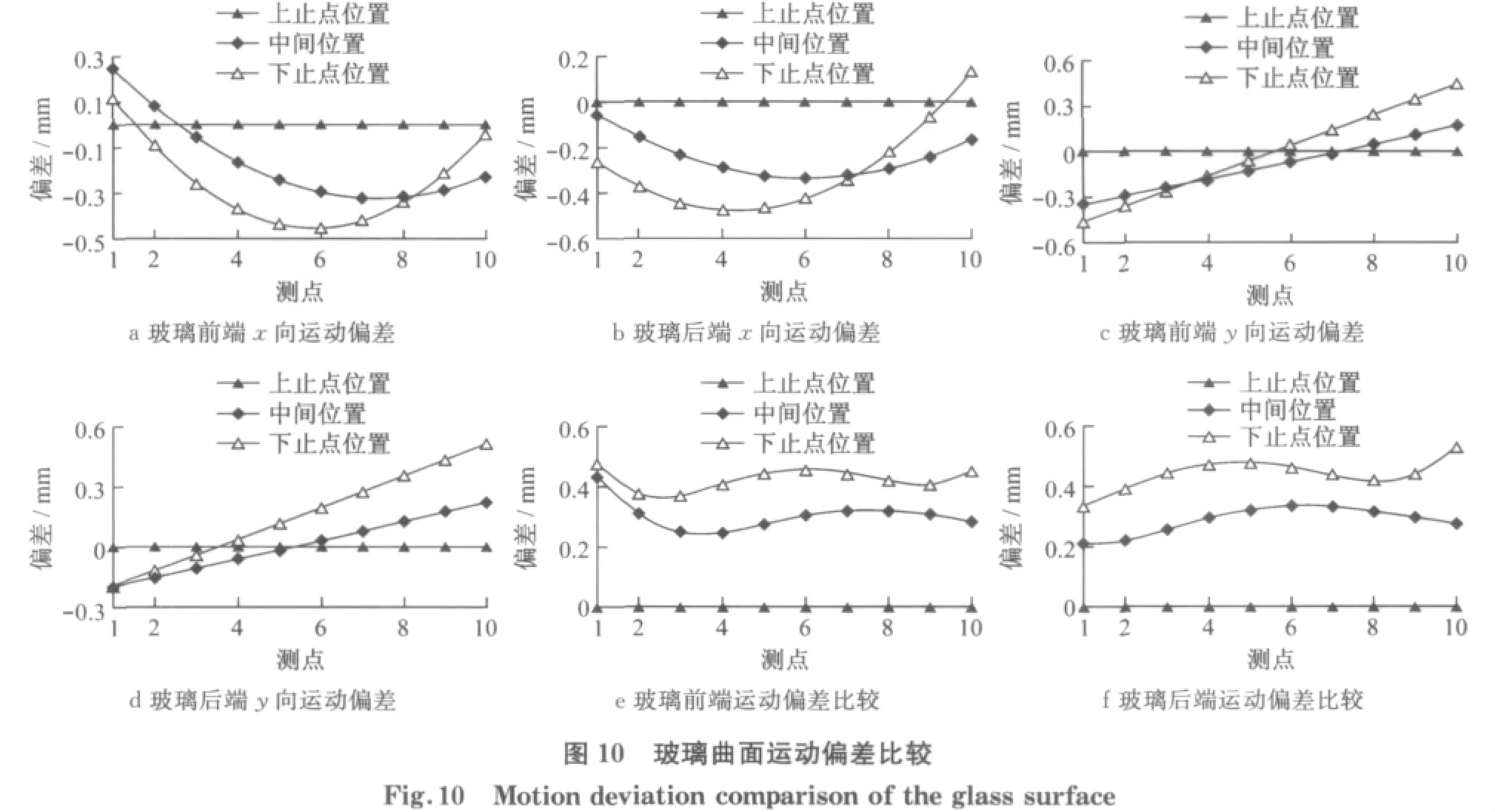
对于鼓形面玻璃的鼓形线运动,可分析玻璃沿升降导轨运动过程中同玻璃导槽中心线的运动偏差情况.分别取B柱一侧与C柱一侧中心线上等距的10个点,图9中所示为前端中心线上2点.测量玻璃下降到中间位置及下止点位置时,这10点与导槽中心线的距离,以此确定玻璃曲面在升降过程中与导槽中心线的运动偏差.由于玻璃曲面的鼓形线运动,所以玻璃与导槽中心线之间的运动偏差实际上包括x向与y向的偏差(如图9),图中坐标系为整车坐标系的平移,可以清楚地看出玻璃曲面沿x向与y向的运动.即,式中:Sshi为玻璃曲面的运动偏差;Sx为玻璃曲面的x向运动偏差;Sy为玻璃曲面的y向运动偏差.具体数值比较见表1.所研究的示例中,玻璃前后边界线同玻璃导槽中心线的运动偏差均在0.6 mm以内,完全达到工程偏差要求.图10是玻璃曲面下降到中间及下止点位置时,相对于车身坐标系而言,玻璃前端与后端同玻璃导槽中心线间的运动偏差比较.方向定义如下:点的x向坐标值小于相应导槽中心线上点的x向坐标值则距离为正,反之为负;点的y向坐标值小于相应导槽中心线上点的y向坐标值则距离为正,反之为负.考虑玻璃密封条对玻璃的反力,如果玻璃升降器托点处位移与角度间隙充分,在密封条的作用下玻璃实际运动偏差值会进一步减小.
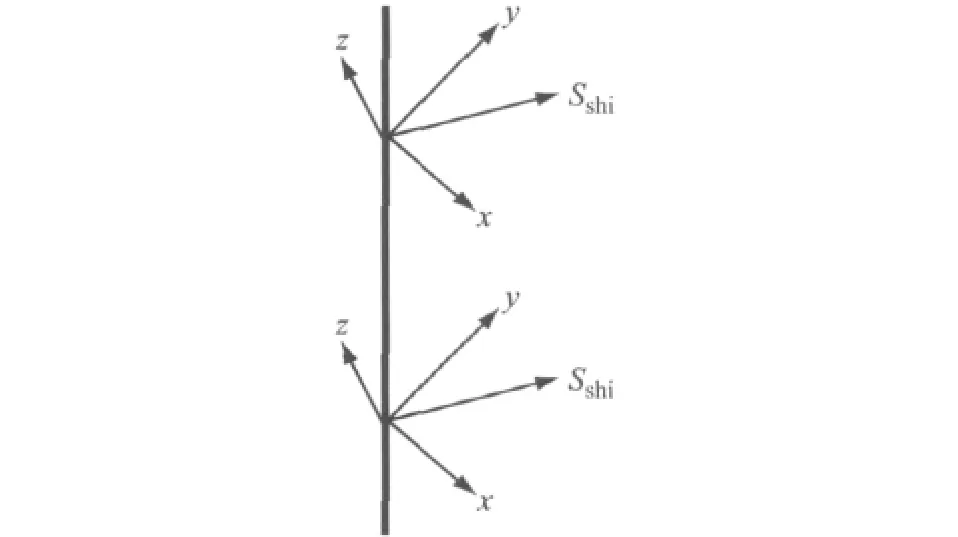
图9 运动合成示意Fig.9 Motion synthesis
经过分析可以知道,运动偏差小于0.6 mm,完全达到工程设计要求标准.说明比例函数方法的正确性与合理性,使用这种方法可以获得设计精度更高的玻璃导轨.
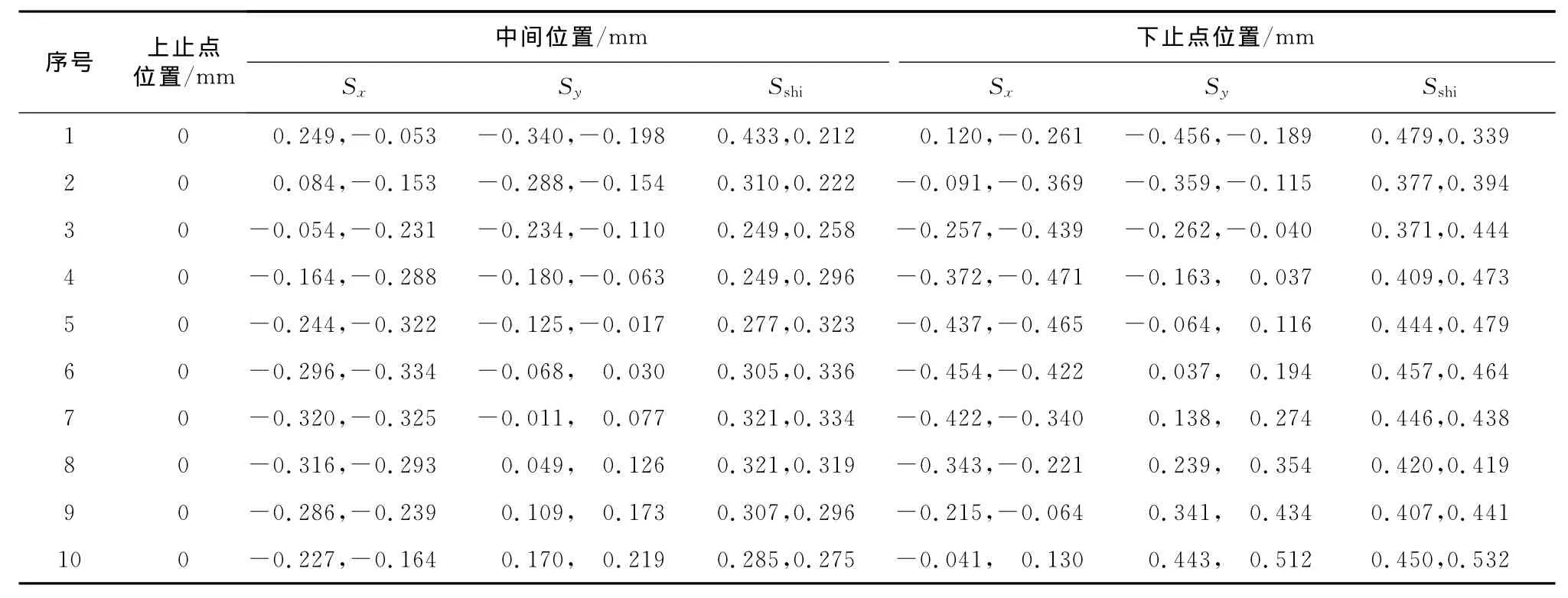
表1 玻璃曲面前端和后端的运动偏差Tab.1 The motion deviation of the front and the rear of the glass surface
4 结论
(1)利用线元几何构造运动方程并结合K-Local-RANSAC算法从车身点云数据得到鼓形面,提出一种以鼓形面拟合双曲面玻璃的方法.该方法拟合精度高,不仅考虑了双曲面的双曲率因素,而且更加符合车身外造型面的设计要求.
(2)根据鼓形线原理,使用比例函数的方法设计玻璃曲面的升降导轨曲线,同时将拟合好的玻璃曲面沿着设计的导轨进行升降运动.经过分析可以知道,玻璃在下降过程中与玻璃导槽中心线的运动偏差在0.6 mm以内,完全达到工程设计要求标准.说明了该设计方法的正确性与合理性,通过这种方法可以获得设计精度更高的玻璃导轨.
[1] 高云凯,赵懿,彭和东.环面玻璃轿车车门设计方法研究[J].汽车工程,2005,27(4):483.GAO Yunkai,ZHAO Yi,PENG Hedong.Design method for car door glass with torus surface[J].Automotive Engineering,2005,27(4):483.
[2] 雷雨成,张平,陈寿昌,等.双曲率车门玻璃的圆环面拟合法[J].汽车工程,2005,27(5):623.LEI Yucheng,ZHANG Ping,CHEN Shouchang,er al.Torus surface fitting for dual curvature car door glass [J].Automotive Engineering,2005,27(5):623.
[3] LIN Chunliang.Virtual experimental design optimization on cable-drive glass guidance system [J].International Journal of Reliability,Quality and Safety Engineering,2002,9(4):317.
[4] LIN Chunliang.Robust design of glass run-channel seal [J].SAE:2004(3):1844.
[5] Kaushlendra Singh,Carl Zaas,Richard Newton.Engineering moveable glass window seals of automotive door using upfront CAE[J].SAE:1998(9):332.
[6] 黄金陵,高云凯,兰凤崇.计算机辅助车身表面造型系统——ABSMS的研制和应用[J].汽车工程,1991,13(2):73.HUANG Jinling,GAO Yunkai,LAN Fengchong.Research and application of ABSMS——auto body surface modeling CAD system [J].Automotive Engineering,1991,13(2):73.
[7] 黄金陵.汽车车身设计[M].北京:机械工业出版社,2007.HUANG Jinling.Vehicle body design [M].Beijing:China Machine Press,2007.
[8] 张量,姜晓峰.基于线元几何的旋转面点云数据旋转轴提取算法[J].计算机研究与发展,2009,46(10):1737.ZHANG Liang,JIANG Xiaofeng.An estimation algorithm of the axis of rotation from 3D cloud data based on line element[J]. Computer Research and Development,2009,46(10):1737.

