格构锚固边坡地震响应的振动台试验研究

杨果林，文畅平,

(1. 中南大学 土木工程学院，湖南长沙，410075；2. 中南林业科技大学 土木工程与力学学院，湖南长沙，410004)

建设中的大(理)—瑞(丽)铁路沿线有大量基覆边坡(厚覆盖层和基岩)，需要采用相应的工程措施对其进行支护，格构锚杆框架支护边坡是其中的措施之一。该铁路位于云南滇西地区，属于高烈度地震多发区，因而需要对沿线的格构锚杆框架支护边坡在地震作用下的动力特性进行研究，为工程设计提供科学依据。岩土边坡动力变形和破坏问题一直是岩土工程和地震工程主要的研究课题，研究方法主要有模型试验和数值分析。边坡动力模型试验方法主要有3种：爆炸模型试验、离心模型试验和振动台模型试验。由于振动台模型试验[1-2]是在地震模拟振动台上输入设计地震波，直接由台面推动测取模型动力特性，因而较好地模拟了地震动力问题，并且能准确再现地震波波形、自动和精确地采集试验数据，无限次地进行地震模拟。尽管振动台模型试验难以解决重力相似问题，但仍然是研究边坡与支挡结构地震变形和破坏问题以及检验数值分析结果的重要手段之一[3-9]。由于通过大型振动台模型试验对边坡和支挡结构的地震动力问题进行的研究较少，本文作者以大瑞铁路沿线格构锚杆框架支护边坡为研究对象，以汶川波作为设计输入地震波，在边坡模型中布置加速度、动位移和动土压力传感器，进行大型振动台模型试验。试验旨在研究地震作用下格构锚杆框架支护边坡的加速度动力响应、动位移和动土压力响应特性。

1 振动台模型试验

试验在重庆交通科研设计院桥梁工程结构动力学国家重点实验室进行，该试验室的地震模拟振动台为大型高性能3轴向6自由度宽频域地震模拟台阵系统，单个台面尺寸为3 m×6 m(宽×长)，承载的最大试件质量为350 kN，工作频率为0.1～50 Hz，水平和竖直向最大位移分别为150 mm和100 mm，水平和竖直向最大速度分别为800 mm/s和600 mm/s，水平和竖直向最大加速度为1g(1g=9.8 m/s2)。

试验拟采集的数据包括：加速度、位移、土压力，利用 Dewetron2010 动态测试数据采集系统自动采集和存储3种传感器的响应数据。

1.1 相似关系设计

本模型试验的控制量为几何尺寸、密度和加速度，其相似常数分别取Cl=8，Cρ=1，Ca=1，模型与原型尺寸的相似比为 1:8，按照相似理论和量纲分析方法[10-12]，确定其余物理量的相似常数如表1所示。

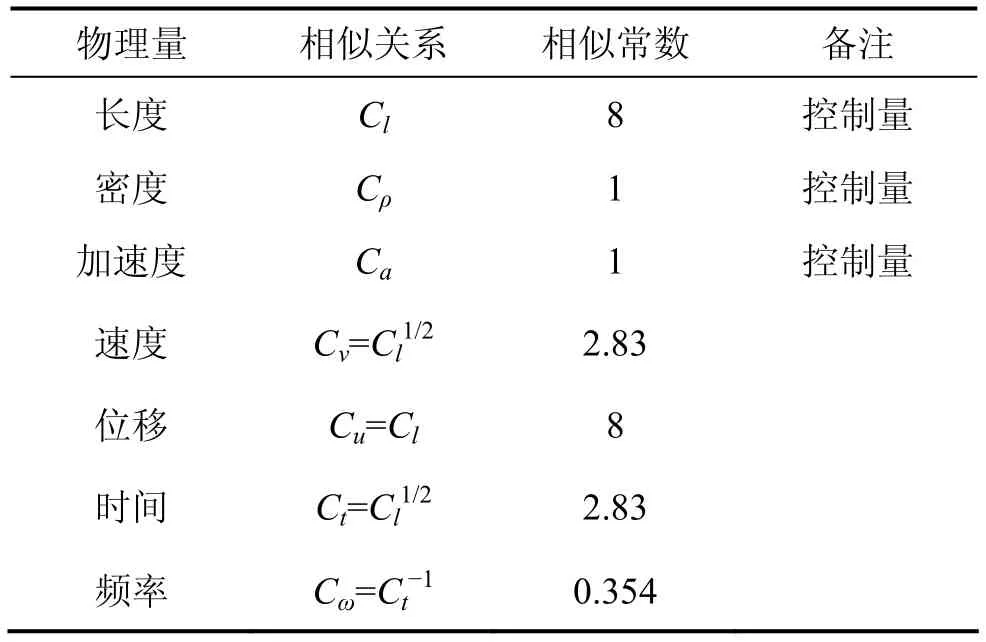
表1 振动台模型试验相似常数Table 1 Similarity coefficients of shaking table test

1.2 模型设计与传感器布设

本模型试验模拟的原型边坡为大瑞铁路 DK10＋400～DK11＋535段基覆边坡。该段边坡地层为碎石土，其碎石为花岗片麻岩，最大粒径为16～20 cm，含量约65%，土质为黏性土，属Ⅲ级硬土。碎石土的天然重度 γ=21 kN/m3，黏聚力c=0 Pa，内摩擦角 φ=35°。本试验模拟边坡高度为12 m，坡度为1:1.25。根据表1的模型相似关系，模型边坡尺寸设计为 150 cm(高)×150 cm(宽)，边坡坡率 1:1.25。

试验采用钢板、型钢和有机玻璃制作的一端开口的刚性模型箱，内空尺寸为 340 cm×150 cm×210 cm(长×宽×高)。边坡模型及其详细尺寸、模型箱和边坡模型全貌分别如图1～3所示。

图1 边坡模型及测点位置图(单位：cm)Fig.1 Slope model and the locations of transducers

图2 刚性模型箱Fig.2 Rigid model box

图3 模型边坡全貌Fig.3 Overall perspective of test model

试验设置12个加速度传感器，6个动位移传感器和4个动土压力传感器，分别测定模型边坡加速度动力响应、护坡动位移和边坡土体动土压力响应特性。所有传感器沿模型边坡中轴线纵剖面布设，01点距基座6 cm，03点距坡顶10 cm，其余测点位置见图1。在格构框架上的1，2和3点等处，设置的水平方向加速度传感器编号为AH1，AH2，AH3；竖直方向的加速度传感器编号为 AV1，AV2，AV3；设置的水平方向动位移传感器编号为DH-1，DH-2，DH-3；竖直方向动位移传感器编号为 DV-1，DV-2，DV-3。在坡内的01，02和03点等处，设置的水平方向加速度传感器编号为 AH01，AH02，AH03；竖直方向的加速度传感器编号为AV01，AV02，AV03；设置的水平方向动土压力传感器编号分别为FH1，FH2，FH3。此外，在 02点处增设竖直方向动土压力传感器，编号为FV2。

在台面、基座底面和顶面分别布设了3个水平方向和3个竖直方向加速度传感器，编号分别为AH-01，AH-2，AH-03以及AV-01，AV-02，AV-03。传感器型号详细说明见表2。

表2 模型试验传感器型号说明Table 2 Specification of each transducer

1.3 试验材料的选取

在模型箱底部浇注高度40 cm的C25混凝土，其上再浇筑表面为圆弧面的C25混凝土，以模拟基质岩层，并将锚杆预埋其中。试验用土为碎石土，土石质量比为4:6，填筑压实度为90%，碎石最大粒径≤2cm，土的最大干密度 ρdmax=2.18 g/cm3，土的最佳含水量wopt=5.34%，c=6.2 kPa，φ=34°。格构框架梁截面为 4 cm的正方形，材料采用加气微粒混凝土，设计抗压强度为5 MPa，混凝土内钢筋和锚杆以直径4 mm的铁丝模拟。

1.4 地震波输入及加载制度

试验采用的地震波有3种：汶川波、大瑞人工合成波和Kobe波。本文主要探讨汶川波(2008，代号为WC)作用下，边坡加速度动力响应、动位移和动土压力响应特性。汶川波分别采用水平单向(X向)、竖直单向(Z向)和水平竖直双向(XZ向)(由X和Z向合成)3种方式加载，代号分别为：WC_X，WC_Z和WC_XZ。激振方向X向和Z向见图1所示，地震波的时间压缩比为 2.83。汶川波具有较丰富的高频成分，在小于0.15 s的短周期范围内，其竖向反应谱比水平规范谱大，而长周期范围内则小很多，其主震持时约为20 s，主频约为5 Hz。汶川波加速度时程曲线见图4。

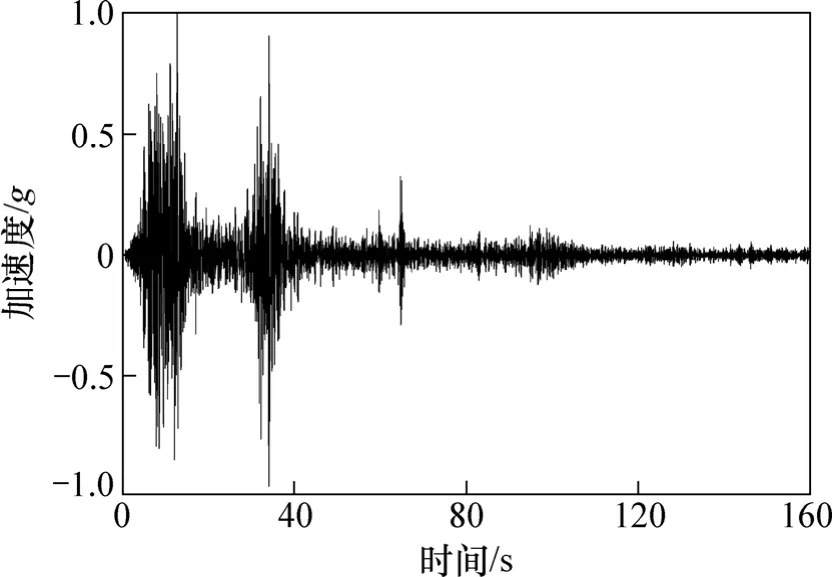
图4 汶川波加速度时程曲线Fig.4 Time-history of Wenchuan seismic wave

试验研究的地震烈度为VII～X，根据文献[13-14]，将相应的加速度峰值调整为：0.1g，0.2g，0.4g和0.6g。试验在此基础上增加了0.8g和1.0g 2种工况，并采用逐级施加地震加速度的方式进行。当X向加载时，按上述加速度峰值逐级加载；当Z向加载时，按X向峰值的2/3折减后逐级进行加载。具体加载制度见表3。

2 边坡加速度动力响应规律

由于每次地震波加载后，台面实测水平和竖直向加速度峰值与激振加速度峰值基本吻合，表明试验是可靠的。此外，由于混凝土基座对台面水平和竖直加速度存在一定的放大效应，且竖直方向表现明显，因此，在进行模型加速度动力响应分析时，以台面加速度传感器响应峰值作为控制点。

以 PGA[15-17]的响应峰值放大系数(Amplification of PGA，记为PGAA)进行边坡模型加速度动力响应分析。规定：X向单向激振时，PGAA为测点加速度响应峰值与台面X向响应峰值实测值的比值；Z向单向激振时，PGAA为测点加速度响应峰值与台面Z向响应峰值实测值的比值；XZ双向激振时，X向PGAA为测点与台面X向响应峰值实测值的比值，Z向PGAA为测点与台面Z向响应峰值实测值的比值。

表3 振动台模型试验加载制度Table 3 Loading rule of shaking table test

2.1 边坡水平方向加速度响应规律

汶川波3种加载方式下，护坡和坡体内各测点X向PGAA随激振加速度的响应规律如图5和图6所示，X向PGAA随坡高的响应规律如图7和图8所示。由图7和图8可见：在X向激振下，6个测点的X向PGAA随激振加速度增大呈现出非线性特征，坡体内各测点的X向PGAA大于护坡，即坡内动力响应强度大于坡面。护坡中下方(AH1和AH2)X向PGAA在激振加速度峰值AXmax≤0.4g时小幅增大，AXmax＞0.4g时小幅减小；上方(AH3)的X向PGAA在AXmax≤0.6g时随激振加速度增大而增大，AXmax＞0.6g时则小幅减小。对于坡体来说，边坡中下部(AH01和AH02)X向PGAA变化平缓，而边坡上部(AH03)则随激振加速度增幅较大。

高程对边坡地震动力响应显著，X向PGAA随坡高表现出非线性增大的特征，但是，AXmax≤0.4g时增大的幅度小于AXmax≥0.6g时的情形。

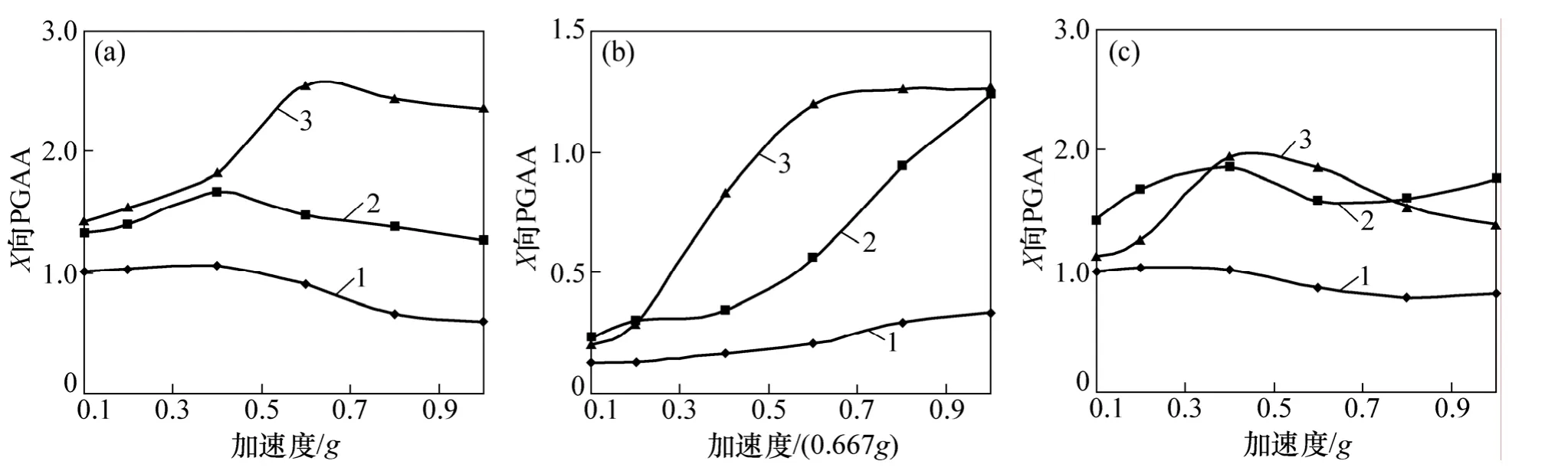
图5 护坡X向PGAA随激振加速度响应规律Fig.5 Response mechanism of X-PGAA of lattice frame with peak exciting acceleration

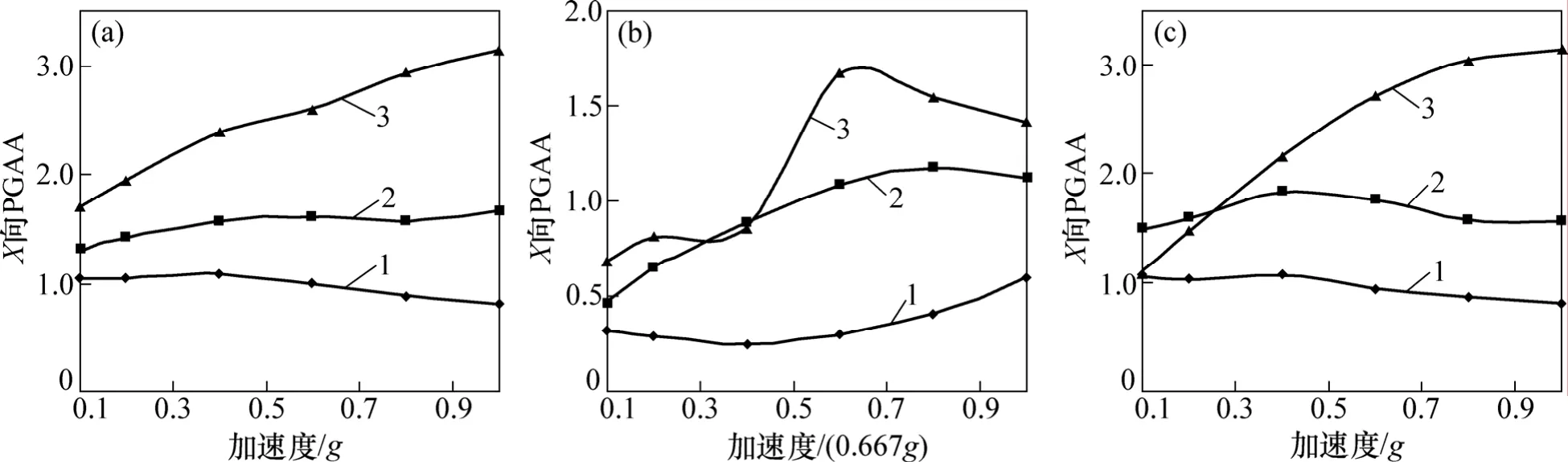
图6 坡体X向PGAA随激振加速度响应规律Fig.6 Response mechanism of X-PGAA in slope with peak exciting acceleration

图7 护坡X向PGAA随坡高响应规律Fig.7 Response mechanism of X-PGAA of lattice frame with slope height

在Z向激振下，激振加速度峰值AZmax≥0.267g时在边坡中部和上部产生较大的水平方向加速度放大效应，且坡内动力响应程度同样比坡面的大。

高程对边坡地震动力响应也较为明显，X向PGAA随坡高同样表现出非线性特征。除 AZmax≤0.133g时护坡上方X向PGAA有减小的趋势，其他加载方式下则随坡高非线性增大。

在XZ向激振下，只有当AXmax≥0.6g时AH03的PGAA继续增大外，其余加载条件下其他测点的PGAA变化不大。边坡中下方坡内外动力响应程度基本一致，而上方坡内动力响应程度比坡面的强。从高程对边坡水平地震动力响应特征来看，边坡下部和中部响应特征相同，即X向PGAA随坡高而增大。边坡上部响应特征多变：护坡X向PGAA除AXmax=0.6g增大外，其余情况下都随坡高而减小；坡体X向PGAA除AXmax≤0.2g减小外，其余情况则是随坡高而增大。这与文献[17-19]中的结论不完全一致。

此外，汶川波XZ向激振下，各测点PGAA并不大于X向单向激振时的情形。

通过上述分析得出：模型边坡X向加速度的放大主要是由于水平方向地震波引起的，并且这种放大效应主要体现在边坡中上方，这与文献[19-20]中的研究结论一致。竖直方向地震波在AZmax≥0.267g时，也会对边坡水平方向加速度产生较大的放大效应。

2.2 边坡竖直方向加速度响应规律

汶川波3种加载方式下，护坡和坡体内各测点Z向PGAA随激振加速度的响应规律如图9和图10所示，Z向 PGAA随坡高的响应规律如图 11和图 12所示。

从图9～12可见：在X向激振下，边坡上方Z向PGAA较为接近X向PGAA，其他测点也产生较大的竖直方向加速度响应，表明X向激振时，水平和竖直方向都产生加速度动力响应[21]。此时坡内外加速度动力响应程度基本一致。Z向PGAA随坡高响应表现出非线性特征。边坡中部Z向PGAA最小，上部最大，呈现出两头大中间小的特征。

图8 坡体X向PGAA随坡高响应规律Fig.8 Response mechanism of X-PGAA in slope with slope height

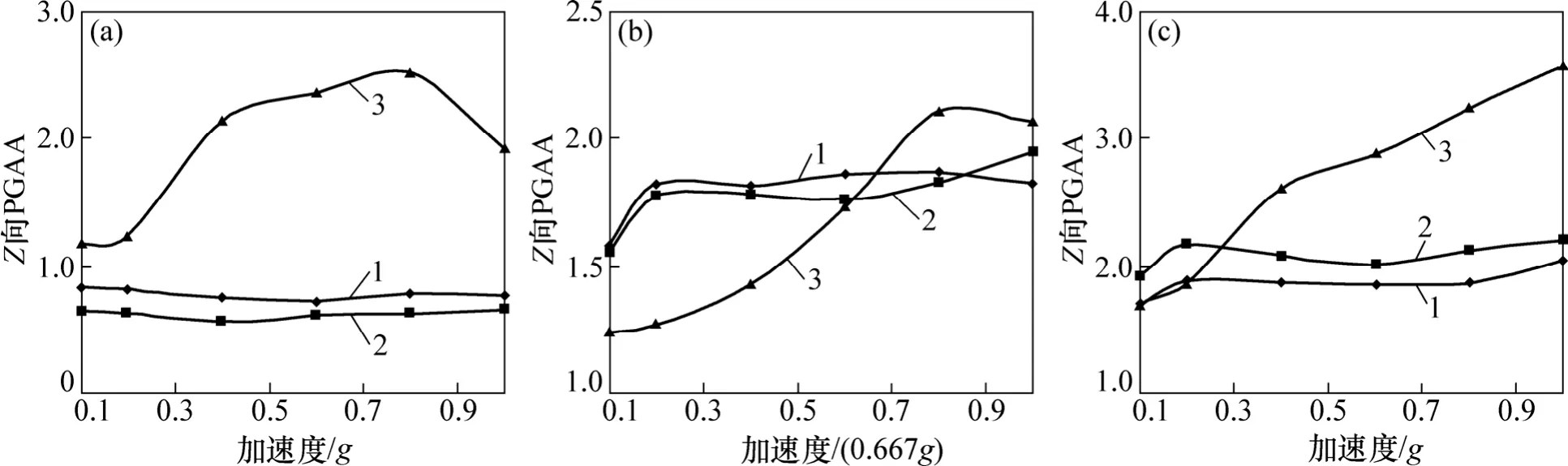
图9 护坡Z向PGAA随激振加速度响应规律Fig.9 Response mechanism of Z-PGAA of lattice frame with peak exciting acceleration

图10 坡体Z向PGAA随激振加速度响应规律Fig.10 Response mechanism of Z-PGAA in slope with peak exciting acceleration

图11 护坡Z向PGAA随坡高响应规律Fig.11 Response mechanism of Z-PGAA of lattice frame with slope height

图12 坡体Z向PGAA随坡高响应规律Fig.12 Response mechanism of Z-PGAA in slope with slope height

在Z向激振下，边坡Z向PGAA总体上随激振加速度增大而增大。AZmax≥0.4g时边坡上部坡内加速度动力响应强度比坡面的大；而对于中下部，坡内动力响应强度总体上比坡面的小。Z向PGAA随坡高响应显著且表现出非线性特征，其中AZmax≤0.267g时Z向PGAA随坡高非线性减小，而 AZmax≥0.4g时 Z向PGAA随坡高非线性增大。

在 XZ向激振下，竖直方向地震动力响应明显，且比水平向动力响应程度显著。Z向PGAA随激振加速度非线性增大。坡内动力响应程度总体上比坡面的弱。高程对边坡竖直方向地震动力响应明显，表现出非线性特征，AXmax≥0.4g时Z向PGAA随坡高而增大。

通过上述分析得出：模型边坡 Z向加速度的放大主要是由于竖直方向地震波引起的。但是水平方向地震波会对边坡上部竖直方向加速度产生较大的放大效应。

3 护坡动位移响应规律

3.1 护坡水平方向动位移响应规律

汶川波3种加载方式下，护坡各测点X向动位移响应规律如图13和图14所示。

从图13～14可见：X向激振下，各测点动位移在激振加速度峰值 AXmax≤0.6g时响应值较小，AXmax≥0.8g时动位移响应幅度较大且永久位移急剧增大。

各测点的永久位移在AXmax≤0.6g时为负值，表明格构框架梁向土体外侧移动；AXmax＞0.6g时都为正值，表明格构框架梁在水平方向向土体方向移动。

在Z向激振下，动位移响应幅度较小，且永久位移的量值很小，表明格构框架梁在X方向上的位移主要由X向激振波所产生。

XZ向激振下，各测点动位移在AXmax≤0.4g时响应值较小，AXmax≥0.6g时动位移响应幅度较大，永久位移逐渐增大且增大的幅度显著。此时，各测点的动位移响应强度特性与X向激振时相同，但永久位移方向相反，表明护坡离开土体向外侧移动，同时绕上端转动。

试验结果表明：动位移响应呈现出非线性特征[22]。这种特性不仅与激振加速度峰值有关，而且与测点位置、地震动方向和持续时间、端部约束等诸多因素有关。

3.2 护坡竖直方向动位移响应规律

汶川波3种加载方式下，护坡各测点Z向动位移响应规律如图15和图16所示。

图13 X向动位移峰值随激振加速度响应规律Fig.13 Response mechanism of X peak displacement with peak exciting acceleration

图14 X向永久位移随激振加速度响应规律Fig.14 Response mechanism of X permanent displacement with peak exciting acceleration

图15 Z向动位移峰值随激振加速度响应规律Fig.15 Response mechanism of Z peak displacement with peak exciting acceleration

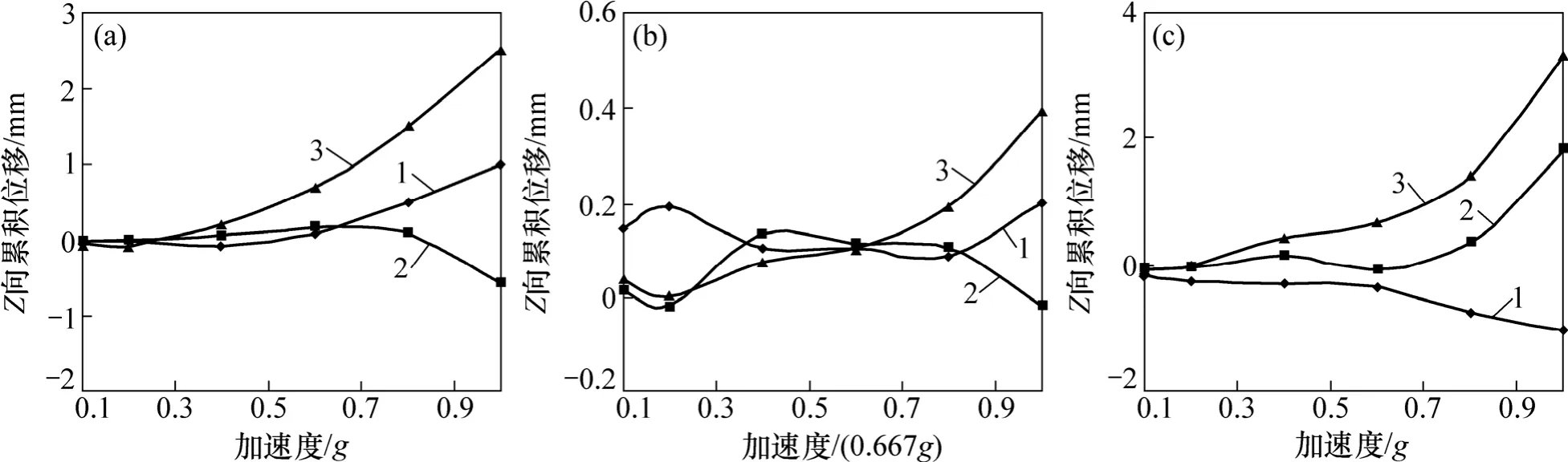
图16 Z向永久位移随激振加速度响应规律Fig.16 Response mechanism of Z permanent displacement with peak exciting acceleration

从图15～16可见：在X向激振下，激振加速度峰值AXmax≤0.6g时各测点竖直方向永久位移较小。对测点永久位移数据分析表明：下端和上端向下移动，中部向上移动，发生弯曲变形。结合X方向的永久位移，格构框架梁发生向土体方向的平移，同时向边坡下方移动。

在Z向激振下，各测点竖直向动位移响应幅度比X向单向激振时更小，且永久位移远小于X向单向激振时的情形。因此，可以认为护坡Z向位移主要由水平方向的地震波所引起。

在XZ向激振下，动位移竖直向响应与X向单向激振时的情形相似。AXmax≤0.6g时，各测点竖直方向永久位移较小，但是，比X向单向激振时稍大。由于下端Z向永久位移为负值，中部和上部为正值，结合X向永久位移，说明格构框架梁在离开土体平移的同时绕上端转动。

4 边坡动土压力响应规律

以激振加速度AXmax=0.6g时的动土压力响应时程曲线(如图17所示)为例，说明汶川波双向激振时动土压力响应规律。

汶川波有2个加速度幅值较大的时段，动土压力响应随之出现了2次突变，且第1次突变比第2次显著。地震动使得边坡产生残余土压力，其大小与测点位置、地震动强度等因素有关。当经历了较强的地震动激振后，再经历同样大小的激振时残余土压力突变不显著，这也就是第2次突变弱于第1次突变的原因。

各测点动土压力随激振加速度响应规律如图 18所示，随坡高的响应规律见图19所示。

图17 汶川波XZ双向激振下(AXmax=0.6g)各测点动土压力响应时程曲线Fig.17 Time-history of seismic earth pressure under XZ excitation (AXmax=0.6g)

图18 各测点动土压力峰值随汶川波激振加速度和激振方式变化情况Fig.18 Response mechanism of peak seismic earth pressure with peak exciting acceleration and directions

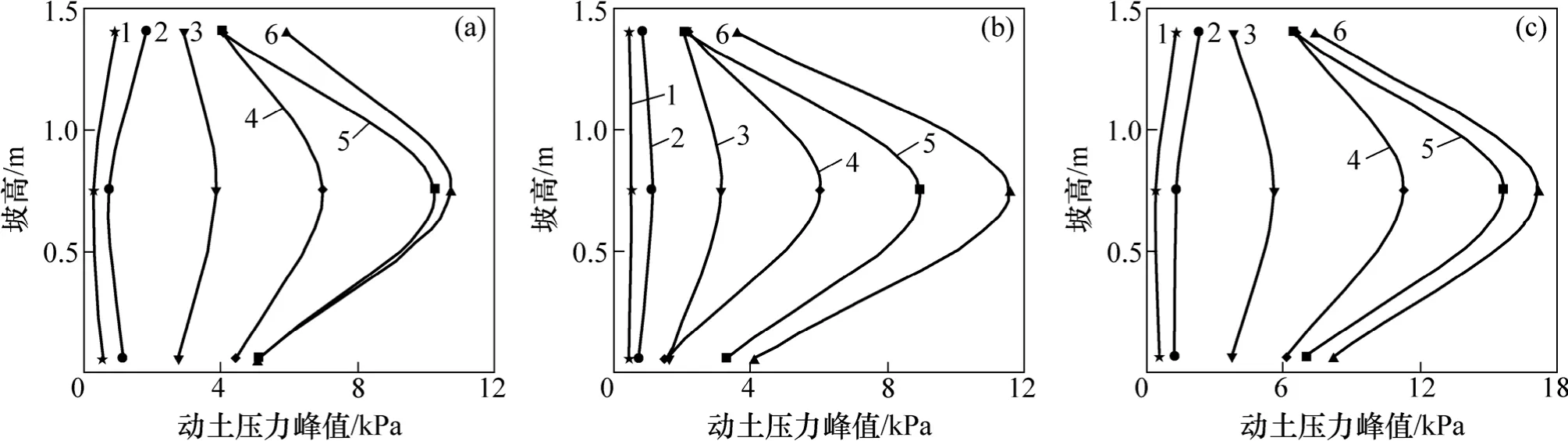
图19 边坡动土压力在坡高上的响应规律Fig.19 Response mechanism of seismic earth pressure with slope height

从图19可见：在汶川波X向、Z向或XZ双向激振下，各测点动土压力峰值总体上都随激振波加速度的增大而增大；X向单向激振时各测点动土压力峰值总体上比Z向单向激振时的稍大。

对FH2和FV2的数据分析表明：汶川波X单向或XZ双向激振下，在激振加速度峰值AXmax≤0.4g时，水平方向和竖直方向动土压力峰值较接近；当 AXmax＞0.4g时，水平方向动土压力峰值远大于竖直方向。在Z向单向激振下，水平方向动土压力峰值同样远大于竖直方向动土压力峰值。

从动土压力在坡高上的响应特征看：无论是X向、Z向单向激振或XZ双向激振下，动土压力表现出非线性特征，当 AXmax≥0.4g(AZmax≥0.267g)时，动土压力峰值的最大值都出现在坡中，呈现出两头小、中间大的非线性分布规律[23]。

5 结论

(1) 3种激振方式都使得边坡产生水平和竖直向加速度动力响应，且这种动力响应及PGAA随坡高变化都呈现出明显的非线性特征。水平向激振主要产生水平方向加速度放大效应，边坡上方响应强度比中下方明显，内部响应强度比坡面明显；竖直向激振主要产生竖直方向加速度放大效应，边坡中上方坡内动力响应强度大于坡面，边坡下方坡内动力响应强度稍弱于坡面；水平和竖直双向激振时，水平向加速度动力响应特征是：强度明显弱于竖直向；边坡中下方PGAA随激振加速度增大的变化幅度较小，随坡高增大呈现出非线性增大；边坡上部响应特征多变，如护坡X向PGAA除激振加速度峰值AXmax=0.6g增大外，其余情况下都随坡高而减小；坡体X向PGAA除AXmax≤0.2g减小外，其余情况则是随坡高而增大。竖直向加速度动力响应特征是AXmax≥0.4g时PGAA随坡高非线性增大。

(2) 3种激振方式下动位移响应都呈现出非线性特征，水平方向动位移响应程度明显比竖直方向的大，水平向的永久位移远比竖直向的大，且竖直向激振时所产生的永久位移几乎可以忽略不计。此外，在水平和竖直双向激振时，水平向动位移响应程度比水平向单向激振时的强，且永久位移量值大但方向相反，竖直向永久位移与水平向单向激振时接近。

(3) 在 3种激振方式下，水平方向动土压力响应程度比较接近；水平向动土压力响应程度大于竖直方向动土压力响应；水平方向动土压力响应都呈现出两头小、中间大的非线性特征，即动土压力峰值的最大值都出现在坡中。

[1]薛守义. 高等土力学[M]. 北京: 中国建材工业出版社, 2007:211-216.XUE Shou-yi. Advanced soil mechanics[M]. Beijing: China Building Materials Industry Press, 2007: 211-216.

[2]黄浩华. 地震模拟振动台的设计与应用技术[M]. 北京: 地震出版社, 2008: 315-340.HUANG Hao-hua. The design and application technology on earthquake simulation vibrating table[M]. Beijing:Seismological Press, 2008: 315-340.

[3]孔宪京, 李永胜, 邹德高, 等. 加筋边坡振动台模型试验研究[J]. 水力发电学报, 2009, 28(5): 152-157.KONG Xian-jing, LI Yong-sheng, ZOU De-gao, et al. Shaking table model tests on soil slope reinforced with geo-grid[J].Journal of Hydroelectric Engineering, 2009, 28(5): 152-157.

[4]Tinawi R, Leger P, Leclerc M, et al. Seismic safety of gravity dams: from shake table experiments to numerical analyses[J].Journal of Structural Engineering, 2000(4): 518-529.

[5]Lin M L, Wang K L. Seismic slope behavior in a large-scale shaking table model test[J]. Engineering Geology, 2006, 86:118-133.

[6]Li Q S, Li Z N, Li G Q, et al. Experimental and numerical seismic investigations of the Three Gorges dam[J]. Engineering Structures, 2005, 27(4): 501-513.

[7]Pitilakis D, Dietz M, Wood D M, et al. Numerical simulation of dynamic soil–structure interaction in shaking table testing[J].Soil Dynamics and Earthquake Engineering, 2008, 28(6):453-467.

[8]Anastasopoulos I, Georgarakos T, Georgiannou V, et al. Seismic performance of bar-mat reinforced-soil retaining wall: Shaking table testing versus numerical analysis with modified kinematic hardening constitutive model[J]. Soil Dynamics and Earthquake Engineering, 2010, 30(10): 1089-1105.

[9]Lee K Z Z, Chang N Y, Ko H Y. Numerical simulation of geosynthetic-reinforced soil walls under seismic shaking[J].Geotextiles and Geomembranes, 2010, 28(4): 317-334.

[10]刘小生, 王钟宁, 汪小刚, 等. 面板坝大型振动台模型试验与动力分析[M]. 北京: 中国水利水电出版社, 2005: 9-20.LIU Xiao-sheng, WANG Zhong-ning, WANG Xiao-gang, et al.Large scale shaking table model tests and dynamic analysis of concrete face rockfill dam[M]. Beijing: China Water Power Press,2005: 9-20.

[11]林皋, 朱彤, 林蓓. 结构动力模型试验的相似技巧[J]. 大连理工大学学报, 2000, 40(1): 1-8.LIN Gao, ZHU Tong, LIN Bei. Similarity technique for dynamic structural model test[J]. Journal of Dalian University of Technology, 2000, 40(1): 1-8.

[12]Iai, Susumu. Similitude for shaking table tests on soil-structure-fluid model in 1-g gravitational field[J]. Soils and Foundations, 1989, 29(1): 105-118.

[13]GB 5001—2001, 建筑抗震设计规范[S].GB 5001—2001, Code for seismic design of buildings[S].

[14]GB 50111—2006, 铁路工程抗震设计规范[S].GB 50111—2006, Code for seismic design of railway engineering[S].

[15]周靖, 陈凯亮, 罗高杰. 速度脉冲型地震地面运动强度表征参数评估[J]. 振动与冲击, 2010, 29(7): 153-158.ZHOU Jing, CHEN Kai-liang, LUO Gao-jie. Evaluation of intensity measures for pulse-like earthquake ground motions[J].Journal of Vibration and Shock, 2010, 29(7): 153-158.

[16]陈跃庆, 吕西林, 李培振, 等. 不同土性的地基-结构动力相互作用振动台模型试验对比研究[J]. 土木工程学报, 2006,39(5): 57-64.CHEN Yue-qing, LU Xi-lin, LI Pei-zhen, et al. Comparative study on the dynamic soil-structure interaction system with various soils by using shaking table model tests[J]. China Civil Engineering Journal, 2006, 39(5): 57-64.

[17]许强, 刘汉香, 邹威, 等. 斜坡加速度动力响应特性的大型振动台试验研究[J]. 岩石力学与工程学报, 2010, 29(12):2420-2428.XU Qiang, LIU Han-xiang, ZOU Wei, et al. Large-scale shaking table test study of acceleration dynamic response characteristics of slopes[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(12): 2420-2428.

[18]陈强, 杨长卫, 张建经, 等. “5.12”汶川地震中高大加筋土挡墙破坏机理研究[J]. 铁道建筑, 2010(9): 73-77.CHEN Qiang, YANG Chang-wei, ZHANG Jian-jing, et al. Study on damage mechanics of high reinforced earth retaining wall under “5.12” Wenchuan Earthquake[J]. Railway Construction,2010, (9): 73-77.

[19]徐光兴, 姚令侃, 高召宁, 等. 边坡动力特性与动力响应的大型振动台模型试验研究[J]. 岩石力学与工程学报, 2008, 27(3):624-632.XU Guang-xing, YAO Ling-kan, GAO Zhao-ning, et al.Large-scale shaking table model test study on dynamic characteristics and dynamic responses of slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(3):624-632.

[20]李昀, 杨果林, 林宇亮. 水平地震作用下绿色加筋格宾挡土墙动力特性试验研究[J]. 中南大学学报: 自然科学版, 2010,41(1): 347-352.LI Yun, YANG Guo-lin, LIN Yu-liang. Dynamic characteristics of green reinforced gabion walls subjected to horizontal seismic loading[J]. Journal of Central South University: Science and Technology, 2010, 41(1): 347-352.

[21]栾茂田, 李湛, 范庆来. 土石坝拟静力抗震稳定性分析与坝坡地震滑移量估算[J]. 岩土力学, 2007, 28(2): 224-230.LUAN Mao-tian, LI Zhan, FAN Qing-lai. Analysis and evaluation of pseudo-static aseismic stability and seism-induced sliding movement of earth-rock dams[J]. Rock and Soil Mechanics, 2007, 28(2): 224-230.

[22]Kramer S L, Smith M W. Modified Newmark model for seismic displacements of compliant slopes[J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 1997, 123(7):635-644.

[23]林彤. 离心模型试验在超高加筋土挡墙中的应用研究[J]. 土木工程学报, 2004, 37(2): 43-46.LIN Tong. Study on the application of centrifuge modeling test to super-elevation reinforced earth retaining wall[J]. China Civil Engineering Journal, 2004, 37(2): 43-46.