基于迭代传播的小基高比立体匹配方法
门朝光,边继龙,李香
(哈尔滨工程大学 计算机科学与技术学院,黑龙江 哈尔滨,150001)
立体匹配是计算机视觉领域中的一个热点问题,它通过匹配2幅或多幅图像获得对应点视差,再通过三角测量原理计算出景物的深度,在计算机视觉、立体测绘、航空摄影测量、遥感等领域有着广泛的应用。目前,虽然基于局部和基于全局的立体匹配方法[1]取得了一定进展,但由于匹配过程是一个病态过程,并且存在着大量的不确定因素,使得立体匹配仍然是一个活跃的研究领域。由于重复纹理、非纹理区域和遮挡的存在使像素点之间的匹配具有很大程度的不确定性,特别当立体像对不是在同一时间获取时,移动或消失的目标会使匹配变得更加困难。为解决上述因素的影响,在立体视觉领域中出现了另一个分支即小基高比立体匹配[2-8]。基于小基高比的立体匹配是指在摄影基线与摄像机高度比值较小,对目标物体进行拍照获得立体像对,再利用立体匹配技术获得对应点视差,最后,根据三角测量原理计算出物体的高程信息。基于小基高比的立体匹配算法中存在 1个相关基本等式[2-4](Central equation of correlation),此等式把测量视差和真实视差联系起来,可在匹配结束后对相关基本等式进行求解以恢复其真实视差。通过求解此等式可以解决小基高比立体匹配中存在的边界膨胀问题即黏合现象。相关基本等式求解问题属于数学上的反问题,具有不适定性[9],需要对相关基本等式进行正则化处理,使问题变得适定可解。本文通过在目标泛函中引入全变差项进行正则化处理,把等式求解问题转化为求解目标泛函的极值问题。目前,数字图像处理领域中变分法受到了许多研究者的关注,它广泛应用于图像复原[10-11]、图像融合[12]、图像分割[13]和立体匹配[14]中。基于变分法的优势在于它能提供一个良好的数学形式体系,而且可以生成亚像素级视差。变分法中的正则化参数选取关系到解的逼近性与数值稳定性,其选取方法可分为先验和后验2类策略。其中,先验策略是在求出正则解之前就已将正则参数确定。这种方法往往具有理论分析价值,在实际中常常难以验证其赖以施用的条件;后验策略则是在计算正则解的过程中根据一定的原则确定与原始数据的误差水平相匹配的正则参数,此方法比较实用。本文采用后验策略根据Morozov偏差原理推导出正则参数选择公式,并设计一个迭代过程进行求解。根据Morozov原理求解正则参数需要了解系统的误差水平,然而,在立体匹配中我们无法事先获知该误差水平。若根据经验设置此误差水平,则在匹配不同的立体像对时需要选择不同的经验值,这会影响算法的适应性,为此本文根据启发式信息估计该误差水平。最后,根据延迟扩散定点迭代思想[15](lagged diffusivity fixed point iteration,FP)获得目标泛函的迭代传播等式,通过共轭梯度法进行求解。
1 相关性分析
假设u和u˜代表立体像对中左右图像,并满足经典立体模型:
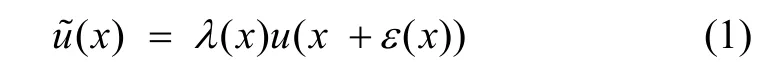
其中:函数 λ(x)在空间上缓慢变化;视差函数 ε(x)是一有界函数,描述立体像对u和之间的几何畸变。在获取立体像对的过程中,若2次成像之间的角度较大即大基高比,则立体像对会受光照变化(例如云层遮挡)、物体遮挡和非朗伯平面等因素的影响而导致它们之间存在较大的辐射差异,致使假设立体模型存在较大的偏差;若2次成像之间的角度较小即小基高比,则可以认为2次成像时的光照条件近似一样而且小角度可以减少物体遮挡,减弱非朗伯平面对辐射差异的
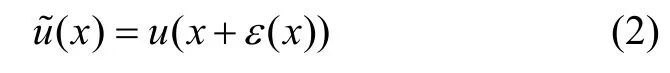
此立体模型假设立体像对u和u˜之间仅存在几何畸变,不存在辐射差异,这种模型只有在基高比 b/h较小时才能成立,而且基高比越小模型越精确。
基于小基高比的立体匹配方法[2-8]属于局部匹配方法,该方法的匹配精度受支撑窗口大小影响。当窗口大小增加时匹配精度随之增加,但同时大窗口也会导致算法在视差不连续处产生误匹配,在立体匹配中把这种误匹配称为黏合现象,这种现象会导致视差图中的前景区膨胀失真。如图1所示,左图像中存在3个点a,b和c,它们分别与右图像中的′,′和′ 3个点相对应,其视差分别为0,db和dc。在匹配时由于b点的支撑窗口包含了建筑物边界致使算法在b点产生错误的视差db=dc,从而导致前景区的建筑物产生膨胀。影响,在这种条件下生成的立体像对可以近似满足这一模型。在小基高比条件下,立体模型可以简化为:

图1 黏合现象Fig.1 Adhesion phenomenon
假设在小基高比模型(2)中真实视差 ε(x)足够小,通过测量视差对这个模型进行一阶近似,可以发现通过相关基本等式(4)能将最大化式(3)所获得的测量视差与真实视差联系起来。
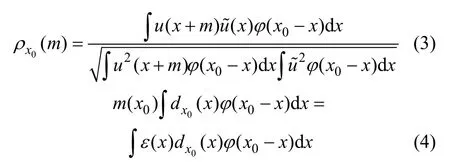
式中:函数 φ ( x0- x )表示以x0为中心的窗口函数;ε(x)表示真实视差函数;0()d x为图像u在x0点的相关密度函数[4],其数学表达式为:

相关密度函数只依赖于参考图像 u,它表达了窗口中心x0周围的边缘方向。通过求解相关基本等式可以解决小基高比立体匹配中存在的黏合现象。Delon等[4]通过 delta函数近似式(4)中的相关密度函数将等式(4)简化为ε(x1)= m(x0),再通过质心校正公式(6)计算出质心的灰度:

然后,在局部窗口内寻找一个与此灰度x1相似的像素位置作为质心位置并将测量视差赋予此位置。虽然通过简单的质心校正取得了一定的成效,但根据该校正公式计算的灰度确定质心位置会导致误差传播。为此,本文提出通过变分原理求解该等式来解决小基高比立体匹配中存在的黏合现象,该方法可以有效减少匹配中存在的黏合现象,提高视差图的准确率。
2 模型分析及求解
2.1 模型分析
小基高比立体匹配中存在的相关基本等式(4)可以表示成形如式(7)的第一类算子方程,其数学表达式为:

由于式(7)中的算子K是1个紧算子,因此,导致求解相关基本等式问题成为1个病态问题。为使等式变得适定可解,经常使用Tikhonov正则化方法对等式进行正则化处理。根据Tikhonov正则化方法,将求解等式(7)问题转化为求解目标泛函极值问题,其目标泛函为:
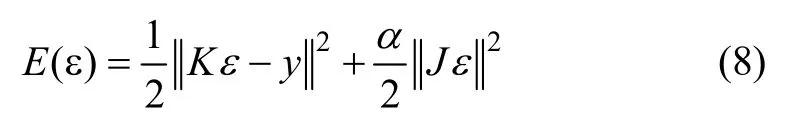

式中:∇ε为ε的梯度,其数学表达式为
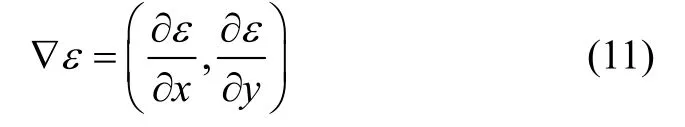
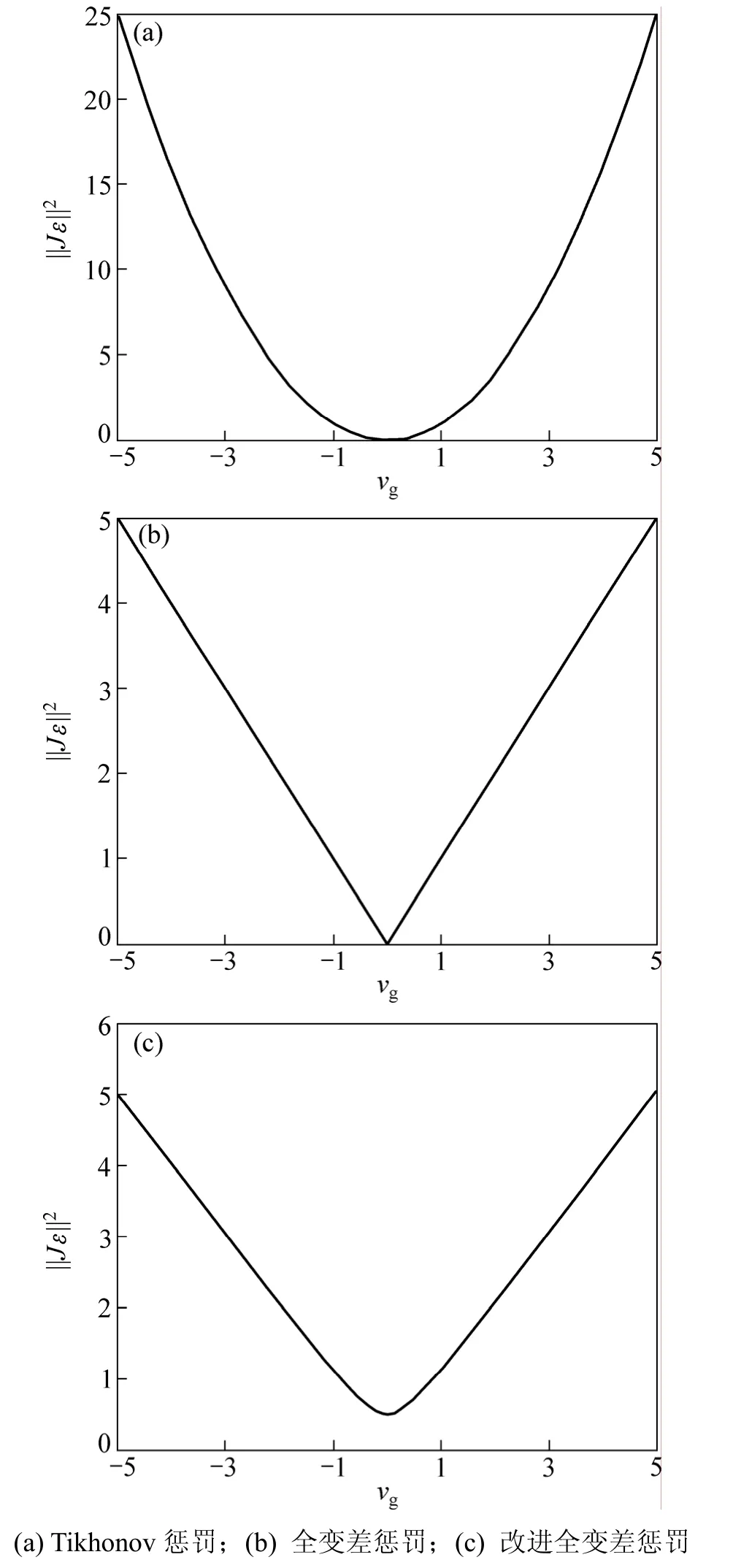
图2 惩罚函数的比较Fig.2 Comparison of different penalty functions
第1种惩罚函数式(9)(如图2(a)所示)在视差函数ε不连续时经常导致虚假振荡(spurious oscillations);第2种惩罚函数式(10)要求视差函数ε处处平滑,然而在物体边界(即视差不连续处)常常会违背这一假设,因此,这2种惩罚函数都不太适合此应用。为保持函数的不连续性,防止在边缘处过度平滑,许多研究者引入了全变差[10-12]来解决此问题,其全变差的数学表达式为:

此惩罚函数的形状如图2(b)所示。由于此惩罚函数不要求视差函数ε处处平滑,因此该函数是一个很好的候选正则函数。然而该函数的欧式范数在0处不可微,为避免这一问题,正则函数修改为:

其修改后的惩罚函数形状如图 2(c)所示。在 β=0时,可以简化为全变差函数
根据修改的全变差惩罚函数式(13)相应的目标泛函可以表达为:
然后,通过对目标泛函E(ε)求导获得该泛函的欧拉-拉格朗日方程:

式中:K*代表伴随算子,其数学表达式为

L(ε)为微分算子,它对函数ω的作用可以通过下式表示:
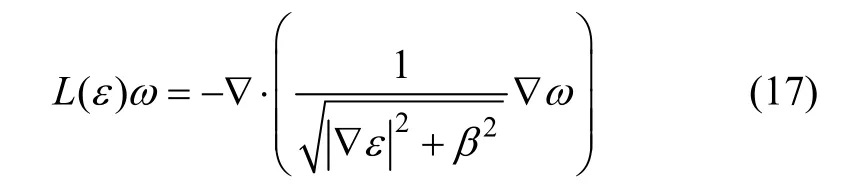
最后,根据Vogel提出的延迟扩散定点迭代思想最小化目标泛函式(14)。其FP迭代可以表达为:

每次迭代必须通过求解线性传播式(18)来获得下一步迭代εk+1,迭代过程的传播率取决于前一迭代εk。
2.2 数值求解
经过离散化处理之后,式(18)转化为超大稀疏线性方程组:

由于系数矩阵A为超大稀疏矩阵,直接通过高斯消除法求解线性方程组的方法不可行,因此,本文通过迭代的共轭梯度法来求解线性方程组,其共轭梯度法如下。
算法1(共轭梯度法[16]):
k=0
r0=b-Ax0
while rk≠0
k=k+1
if k=1
p1=r0
else
βk=(rk-1)Trk-1/(rk-2)Trk-2
pk= rk-1+βkpk
end
αk=(rk-1)Trk-1/(pk)TApk
xk=xk-1+αkpk
rk=rk-1-αkApk
end
x=xk
3 正则化处理
3.1 正则参数选择
由于正则化参数α的选取关系到解的逼近性与数值稳定性,为此,根据Morozov原理[17]选择此参数以获得较为精确的视差。Morozov原理阐述了怎样利用观测数据选择正则参数 α,它在线性反问题领域中受到了很大关注。由于正则化产生的误差等于观测数据所引起的误差,因此,可以根据这一原理选择正则参数α:
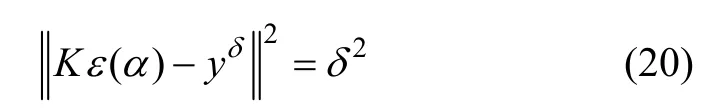
在计算正则参数的过程中需要利用以下几个法则,本文在此给出这些法则和其证明过程。令F(α)是关于正则参数的函数,其数学表达式为:

法则1 对任意α>0,式(21)存在惟一最小化解,它可以描述成下面系统的解:

或者用内积可表示为:

法则2 F(α)的一阶导数和二阶导数可以表示为:

证明:

根据式(23)可得:
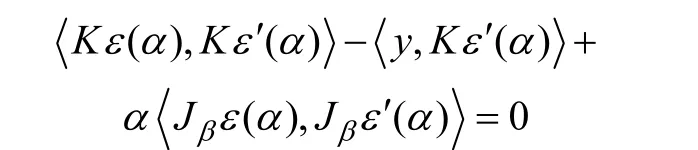
因此,可得:
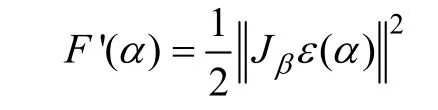
法则 3 F(α)是关于正则参数的函数,对任意α>0,存在如下等式:

证明 根据法则1,有如下等式成立:

对上述等式两边关于α求导得:

根据法则2,上述等式可以转化为:

对等式两边积分得:

根据 F(α)和 F′(α)可以将式(20)转化为:
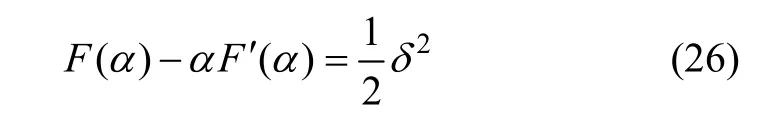
为了获得合理的正则参数,根据Morozov原理推导出正则参数选择方法。为推导模型函数,对式(25)的第3项进行如下近似:

式中:T1是待定常数。通过上述近似,式(25)可以简化为:

对等式(28)两边积分可得:

为简化正则参数α的计算,令m(0)=0,其模型函数m(α)的表达式可以简化为:
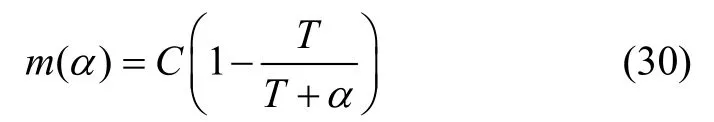
对模型函数m(α)关于α求导得:

最后,通过迭代方法求解正则参数α,具体算法如下。
(1) 根据式(21)和式(24)计算 F(αk)和 F′(αk),再根据式(32)计算Ck和Tk。

通过求解式(32)可得:
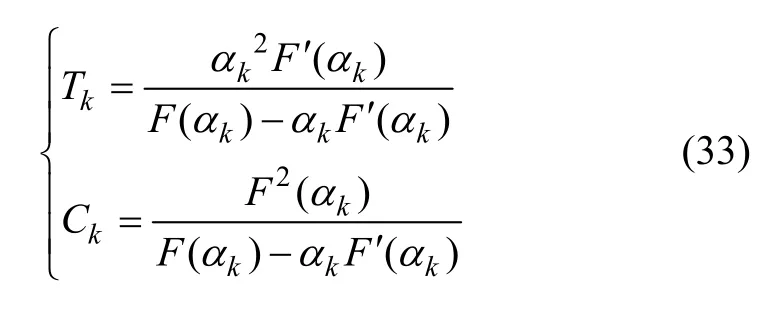
(2) 根据式(30)和式(31)计算 m(αk)与 m'(αk)。
(3) 根据 Morozov偏差方程(26)计算正则参数αk+1。

3.2 估计误差水平
计算正则参数时需要使用观测误差水平δ,然而,立体匹配中往往无法事先获知该误差水平。为了能精确的估计正则参数,在计算正则参数之前首先利用启发式方法估计该误差水平。根据Morozov原理有如下不等式关系成立:
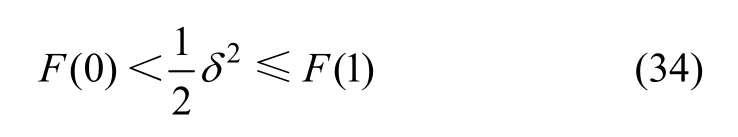
利用式(34)可推导出误差观测水平的存在区间:
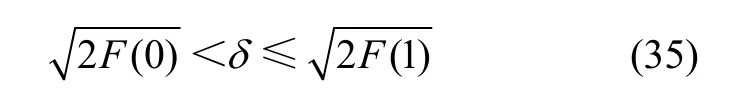
在数值实现过程中,利用模型函数m(α)预测观测误差δ:

具体实现过程如下:
(1) 给定比例常数 σ ∈ [ 0 .5,1]和初始正则参数 α0>0。
(2) 利用式(21)和式(24)计算 F(α0)和 F'(α0)。然后,利用式(37)计算式(30)中的参数C和T。

再利用式(38)计算正则参数α1:

式中:y0为曲线 y=m(α)上点(α0,m(α0))的切线与 y 轴的截距,其数学表达式为
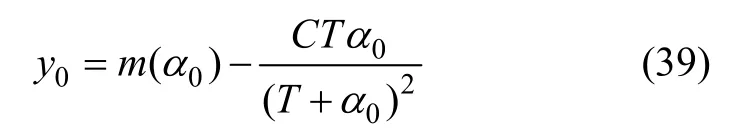
(3) 根据步骤(2)中计算的正则参数α1,利用式(21)和式(24)计算 F(α1)和 F'(α1),再利用式(25)计算参数C0,然后,利用式(29)和式(40)计算参数C1和T1。

利用式(29)计算m(0)和m(1),误差δ表示为:

3.3 算法总体流程
基于迭代传播的小基高比立体匹配方法是在Delon等[4]提出的基于多分辨率的小基高比立体匹配方法的基础上通过对匹配中存在的相关基本等式进行迭代求解来恢复其真实视差值。该方法可以减少小基高比立体匹配过程中因匹配窗口跨越边界而导致的黏合现象,立体匹配中的这种黏合现象会导致视差图中前景区产生“膨胀”。算法具体流程如下:
(1) 利用小基高比立体匹配算法[4]获得初始测量视差ε0,并给定比例常数σ和初始正则参数α0。
(2) 利用3.2节中的算法获得误差水平δk。
(3) 利用3.1节中的算法获得正则参数αk。
(4) 利用共轭梯度法求解线性方程组(19)获得视差 εk+1,若或者 k ≥kmax则停止迭代;否则,k=k+1,转入步骤(2)继续迭代。
4 实验分析
本实验使用 CNES提供的航空摄影像对Toulouse(如图3(a),(b)所示)对本文算法的合理性进行验证。这幅立体像对是1幅航空影像图,基高比约为0.045,地面分辨率为 R=0.5,其获取时间间隔为 20 min,这导致立体像对中存在明显的运动和阴影移动,增加了视差估计的难度。实际上,理想的小基高比立体像对的2次获取时间间隔较小,这样可以有效的减少立体像对间的辐射差异和景物运动对匹配产生的不利影响。

图3 Toulouse立体像对Fig.3 Toulouse stereo images
理论上讲,小基高比条件下形成的立体像对非常相似,具有较小的视差搜索范围。这幅立体像对的视差范围为[-2,2],可近似模拟小基高比条件下的立体像对,这种相似性使匹配过程变得更容易。图 3(a)和(b)所示为这幅立体像对的左右图像,看出它们非常相似,具有较小的几何畸变与视差搜索范围。其真实视差图如3(c)所示。图4(a)为Delon等[4]提出的基于多分辨率的小基高比立体匹配方法获得的实验结果,通过与真实视差图对比可以看出该方法已经获得了较好的效果,但是,在背景处还是存在一些明显的误匹配,而且在物体边界处伴随着较多黏合现象(如图 4(b)所示)。图4(c)所示为由本文算法生成的视差图。从图4可见:由本文算法生成的视差图中场景各主要组成部分都清晰地检测出来,特别是建筑物四周只发生微小变化的那些部分也都被清晰地检测出来。通过对比图4(b)和 4(d)可以看出:本文算法的黏合现象要明显少于文献[4]中的黏合现象,而且该算法生成的视差图的准确率高达95%以上。
为验证小基高比立体匹配的高程精度,本实验使用由空间机电研究所提供的1幅带有真实高程信息的小基高比立体像对(如图 5(a)和(b)所示)。该立体像对的基高比约为0.05,地面分辨率为0.2。在该实验中,根据本文算法生成的视差图(如图 5(c)所示)计算几个主要建筑物的高程信息,这些建筑被标记在图5(d)中,对应建筑物的视差、计算高程和真实高程如表1所示。高程计算公式如下:式中:δ为视差;B/H为基高比;R为地面分辨率。从表1可知:该算法具有较高的高程精度,其平均高程误差为0.33 m,像元匹配差异精度为0.082 5,优于1/10个像元。

图4 黏合现象比较Fig.4 Comparison of adhesion phenomenon

表1 高程信息Table 1 Information of DEM

图5 高程精度验证Fig.5 Verification of DEM accuracy

5 结论
(1) 根据启发式信息估计视差误差水平,解决了先验参数估计问题,使匹配算法具有更强的适应性。
(2) 所提出的迭代正则参数选择方法解决了正则解的稳定性与逼近性问题,使匹配算法获得了更加精确的视差。
(3) 通过共轭梯度法求解目标泛函的迭代传播等式加快了匹配算法的收敛速度。
(4) 该方法能有效地减少小基高比立体匹配中的黏合现象,提高视差图的准确率,其视差图的准确率可达95%以上,且亚像素精度可优于1/10个像元。
[1] 罗三定, 陈海波. 基于区域增长的自适应窗口立体匹配算法[J]. 中南大学学报: 自然科学版, 2005, 36(6): 1042-1047.LUO San-ding, CHEN Hai-bo. Stereo matching algorithm of adaptive window based on region growing[J]. Journal of Central South University: Science and Technology, 2005, 36(6):1042-1047.
[2] Delon J. Fine comparison of images and other problems[D].Paris: ENS Cachan. Mathematics Department, 2004: 89-108.
[3] Facciolo G. Variational adhesion correction with image based regularization for digital elevation models[D]. Montevicleo:University of the Republic. Engineering College, 2005: 37-49.
[4] Delon J, Rouge B. Small baseline stereovision[J]. Journal of Mathematical Imaging and Vision, 2007, 28(3): 209-223.
[5] Igual L, Preciozzi J, Garrido L, et al. Automatic low baseline stereo in urban areas[J]. Inverse Problems and Imaging, 2007,1(2): 319-348.
[6] Morgan G L K, LIU Jian-guo, YAN Hong-shi. Sub-pixel stereo matching for DEM generation from narrow baseline stereo imagery[C]//Proceedings of International Geoscience and Remote Sensing Symposium. Boston: IEEE, 2008: 1284-1287.
[7] Sabater N, Blanchet G, Moisan L,et al. Review of low-baseline stereo algorithms and benchmarks[C]//Proceedings of Image and Signal Processing for Remote Sensing XVI. Toulouse: IEEE,2010: 1-12.
[8] Morgan G L K, LIU Jian-guo, YAN Hong-shi. Precise subpixel disparity measurement from very narrow baseline stereo[J].IEEE Transactions on Geoscience and Remote Sensing, 2010,48(9): 3424-3433.
[9] 王彦飞. 反问题的计算方法及其应用[M]. 北京: 高等教育出版社, 2007: 3-15.WANG Yan-fei. Computational method for inverse problem and their application[M]. Beijing: High Education Press, 2007: 3-15.
[10] Aujol J F. Some first-order algorithms for total variation based image restoration[J]. Mathematical Imaging and Vision, 2009,34(3): 307-327.
[11] Beck A, Teboulle M. Fast gradient-based algorithms for constrained total variation image denoising and deblurring problems[J]. IEEE Transactions on Image Processing, 2009,18(11): 2419-2434.
[12] Mrityunjay K, Sarat D. A total variation-based algorithm for pixel-Level image fusion[J]. IEEE Transactions on Image Processing, 2009, 18(9): 2137-2143.
[13] Chung G, Vese L A. Image segmentation using a multilayer level-set approach[J]. Computing and Visualization in Science,2009, 12(6): 267-285.
[14] Benari R, Sochen N. Stereo matching with Mumford-Shah regularization and occlusion handling[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(11):2071-2084.
[15] Vogel C R, Oman M E. Iterative methods for total variation denoising[J]. SIAM Journal on Scientific Computing, 1996,17(1): 227-238.
[16] Golub G H, Loan C F V. Matrix computations[M]. London:Johns Hopkins Univ, 1996: 520-532.
[17] Kunisch K, ZOU Jun. Iterative choices of regularization parameters in linear inverse problems[J]. Inverse Problems, 1998,14: 1247-1264.

