基于动态响应的?无级变速传动系统速比控制策略

胡建军，何铮斌，刘永刚，秦大同

(重庆大学 机械传动国家重点实验室，重庆，400044)

无级自动变速传动(Continuously variable transmission，CVT)是汽车理想的传动方式，具有较宽的速比变化范围，通过对速比连续地调节，可保证发动机在理想的工作线上运行，获得传动系与发动机的最佳匹配，从而提高车辆的动力性和经济性，减少排放污染[1-3]。随着世界能源的紧缺和汽车排放标准的提高，人们日益重视CVT汽车的研究与开发。速比控制是CVT传动系统的关键技术之一，CVT速比变化率对汽车动态特性品质具有至关重要的作用[4-5]，因此有必要对 CVT的速比进行恰当的控制以提高汽车的动态特性[6-7]。在CVT速比控制中，目标速比由发动机最佳工作点和当前的车速决定。理想的运行工况为通过速比连续变化使发动机工作点沿最佳工作曲线移动。在汽车实际的行驶工况中，由于无级变速传动系统自身的结构特点，导致整车在动态工况下对加速踏板响应存在迟滞现象[8]。当速比变化率过大时，汽车加速度具有负的作用效果，加速踏板踏下后，汽车反而出现减速现象。而速比变化率过小时，汽车加速响应过慢，加速时间过长。本文作者在考虑动力传动系统迟滞影响的基础上，以提高无级变速传动系统动态性能为目标，对无级变速传动系统速比控制的方法进行了研究，并进行了仿真验证。

1 无级变速传动系统的匹配规律

1.1 发动机输出转矩模型

研究表明，发动机的外特性曲线和部分负荷特性曲线均是发动机油门开度α和发动机转速ne的函数，即 Te=f(α，ne)(其中，Te为转矩)。在一定的油门开度下，发动机输出转矩曲线可由实验数据3次插值拟和达到满意的精度，因此可用有限的实验数据建立发动机数值模型。图1所示为发动机油门开度、转速及输出转矩对应数据所形成的曲面，但它仅表示发动机在稳态工况下的输出转矩。

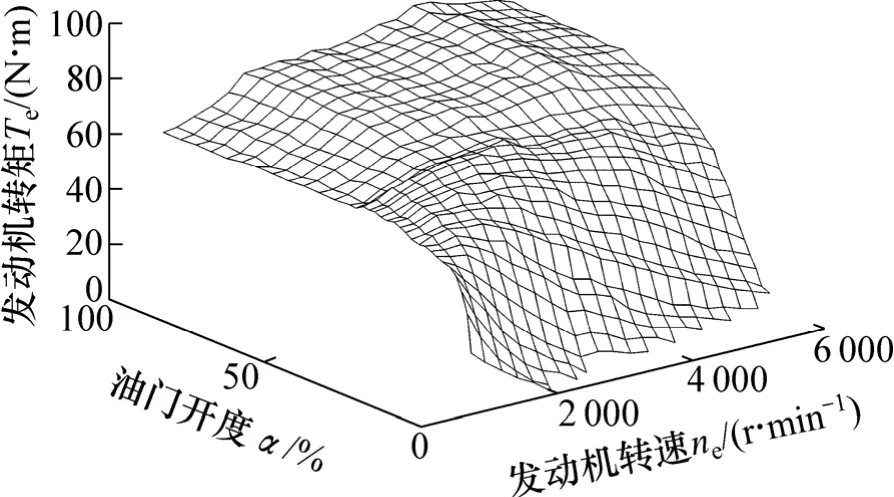
图1 JL472Q1发动机的稳态输出扭矩Fig.1 Steady-state output torque of engine JL472Q1

1.2 发动机油耗模型

发动机负荷特性曲线给出了在不同转速下发动机负荷与有效燃油消耗的关系。根据每个发动机下的负荷特性曲线获得不同转速下发动机的功率与比油耗的关系 ge=ge(ne，pe)，可建立发动机有效燃油消耗率与发动机转速和转矩的关系曲面。发动机油耗的数值模型如图2所示。由于发动机动态特性对发动机的燃油消耗率影响不大，因此，用稳态的油耗数值模型近似代替其动态油耗模型。利用发动机油耗模型可得发动机万有特性图如图3所示。

图2 JL472Q1发动机燃油消耗模型Fig.2 Fuel consumption map of Engine JL472Q1

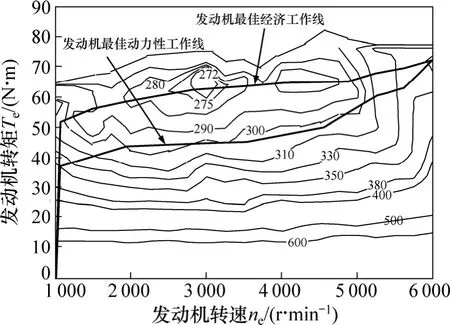
图3 JL472Q1发动机万有特性曲线Fig.3 Universal characteristic curve of engine JL472Q1

1.3 发动机最佳经济性和最佳动力性控制

在每个发动机油门开度下,为保证汽车以不同车速在任意道路阻力下行驶,应有相应的速比保证发动机在所要求的最优工作点运行。

速比控制分为最佳经济性控制和最佳动力性控制2种模式，分别对应着使发动机工作在最佳经济状态和最佳动力状态。发动机最佳动力线和最佳线分别表示发动机油门开度与发动机转速的调节特性曲线，在不同的油门开度下有不同的发动机最佳经济性和最佳动力性目标转速 ne_tgt[9]。再根据当前车速调整速比，使发动机实际转速跟踪目标转速。目标速比计算公式为

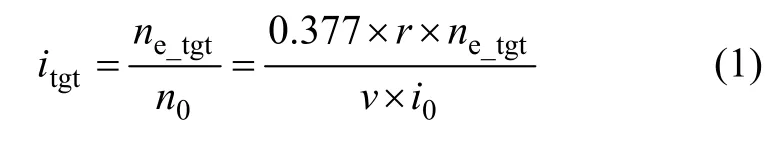
式中：n0为无级变速器输出转速；r为轮胎半径；v为车速；i0为主减速器的速比。

图4所示为发动机最佳经济性和最佳动力性工作时无级变速传动的目标速比。根据汽车的行驶情况通过控制无级变速传动比就可以控制发动机的工作点,实现汽车的最佳经济性运行和最佳动力性运行。

1.4 无级变速传动系统常规控制

常规控制方法是以发动机稳态工况下的最佳经济性和最佳动力性工作线为依据，对 CVT速比进行控制。在常规控制中，以无级变速传动的最佳经济性目标速比和最佳动力性目标速比为控制原则，通过控制无级变速传动系统的速比连续变化来使发动机工作在最佳转速，充分发挥发动机的性能，实现发动机在最佳燃油经济性和最佳动力性曲线上运行。

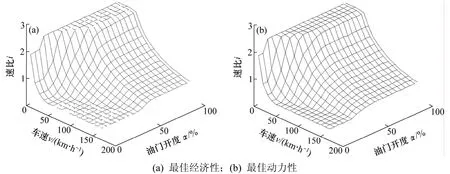
图4 无级变速传动目标速比Fig.4 Target ratio of CVT

图5 常规控制下加速时的动态特性Fig.5 Acceleration dynamic characteristics under conventional control

为了研究常规控制下汽车无级变速传动系统的动态特性，对汽车行驶时加速过程进行了仿真分析。系统主要参数如下：CVT速比范围为 0.498～2.502；整车质量M=1 190 kg；主减速比i0=5.993 4；车轮半径r=0.274 m；迎风面积 A=2.19 m2；空气阻力系数CD=0.32；发动机的转动惯量Ie=32 g·m2；无级变速器主动轮轴上的转动惯量 IT=66 g·m2；滚动阻力系数f=0.018。

汽车无级变速传动系统的最大速比变化率为 2，初始状态下的油门开度为 20%，汽车车速保持在 90 km/h，汽车在常规控制下以小油门和大油门加速时的动态特性如图5所示。由图5可知：汽车在常规控制下以小油门加速时，加速平稳且汽车具有良好的动态性能。当油门急速增到全油门时，汽车的加速度迅速下降到负值，然后再快速增大，汽车出现了减速现象。由仿真结果可知，常规控制方法适用于小油门加速也就是非紧急加速时的情况，而当在大油门加速即紧急加速时，就会出现负加速度现象，因此有必要研究汽车动态时的速比控制方法。

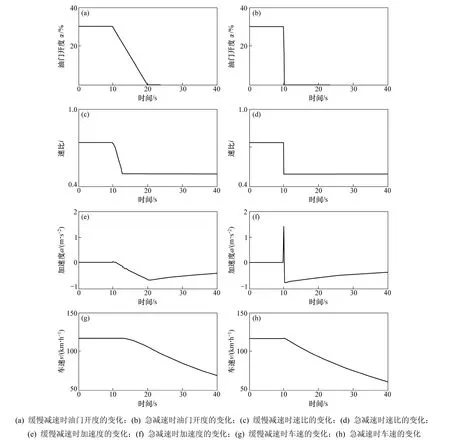
图6 常规控制下减速时的动态特性Fig.6 Deceleration dynamic characteristics under conventional control

为了研究常规控制下无级变速传动汽车减速时的动态特性，对汽车行驶时减速过程进行了仿真分析。CVT的最大速比变化率为2，初始状态下的油门开度为30%，汽车车速保持在120 km/h。汽车在常规控制下减速时的动态特性如图6所示。由图6可知，汽车在缓慢制动时，汽车的平顺性好，制动减速时间比较长且制动减速的响应时间久，而在减速时，汽车的制动时间短，但会出现加速现象，这对汽车的平顺性不利。因此常规控制方法只适合非紧急制动过程，在紧急制动时不能够使汽车的减速响应速度和平顺性和谐统一。因此需要研究动态时的控制方法使汽车的减速响应速度和平顺性和谐的统一，从而提高汽车的动态性能。

2 无级变速传动系统动态模型

在无级变速传动中，当汽车加速时, 为控制发动机在目标区运行, 无级变速器的速比将随时发生变化。在常规控制方法下，由于传动系转动惯量的影响，造成在升挡时驱动转矩降低，而在降挡时驱动转矩升高。本文研究的是当车速达到闭锁车速后，液力变矩器闭锁，传动方式变为纯机械传动，此时传动系统的动态模型简化为如图7所示的无级变速动力传动结构简图，并分析速比变化时动力传动系转动惯量变化的影响[9-11]。

以驱动轴表示的汽车动力传动系转动惯量为：

式中：Ie为发动机的转动惯量；IT为无级变速器主动轮轴上的转动惯量；i为无级变速器带传动速比；Is为无级变速器从动轮轴上的转动惯量；Id为驱动轴轴上的转动惯量。

根据能量守恒定律，动力传动系存在以下关系：

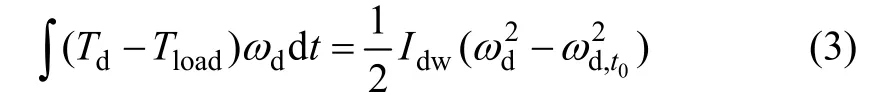
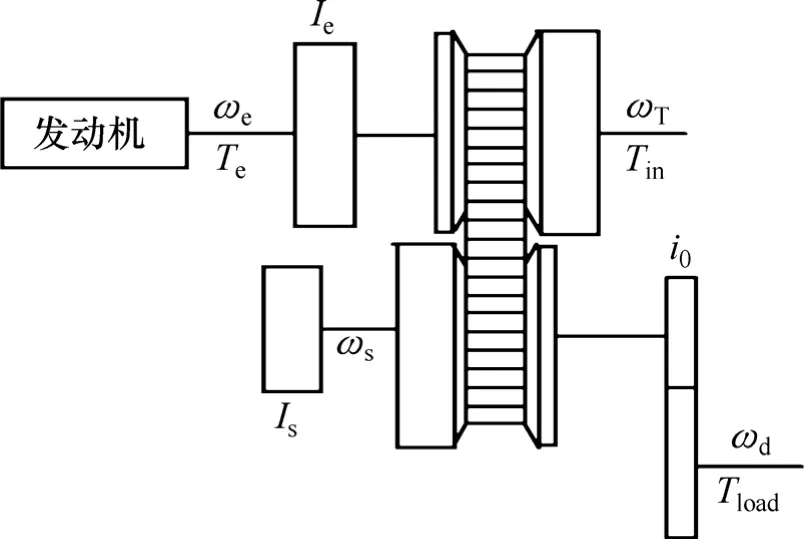
图7 无级变速动力传动系结构简图Fig.7 CVT structure layout

式中：Td为驱动转矩；Tload为道路负载转矩；ωd为驱动轴角速度；ωd,t0为积分开始点t0时驱动轴的角速度。两边对时间求导得：

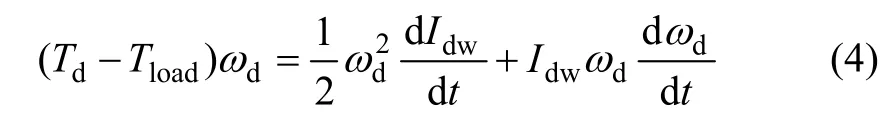
式(2)两边对时间求导得：

将式(5)代入式(4)得

式(6)右边的第二部分就是速比变化时，在驱动轴上产生的惯性矩Tc，将Tc转化到发动机输入轴上的等价惯性转矩为

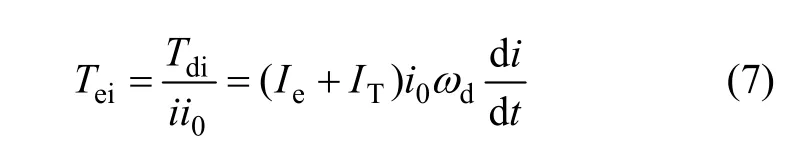
则

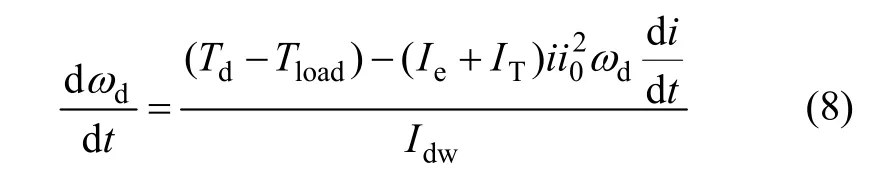
由式(8)可以看出：速比变化率对驱动轴角加速度有负的作用效果，因此要限制速比变化率的最大值。由传动系统输出轴角速度可得汽车行驶加速度：

则加速度的表达式为：

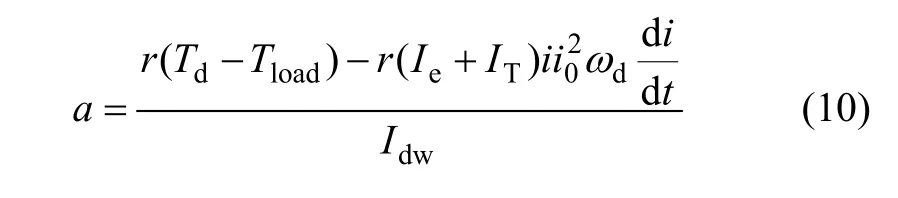
由此可知，速比变化率对加速度有负的作用效果，若速比变化率过大则汽车的加速度会出现负值。

在常规控制方法中出现负加速度是因为没有考虑汽车行驶过程中的速比变化率的影响因素，当速比变化率过大时，速比变化率对汽车加速度具有负的作用效果。因此在控制CVT速比时要考虑CVT速比变化率的影响因素。

3 CVT速比变化率控制

3.1 CVT速比变化率控制方法

由汽车加速过程的仿真分析可知，CVT速比变化率对汽车加速时的动态特性影响显著，因此要通过控制CVT速比来实现对CVT速比变化率的控制。而汽车行驶过程中的驱动功率受后备功率的限制，所以对CVT速比变化率的控制要考虑后备功率的影响因素[12-13]。根据汽车行驶功率平衡方程可得汽车行驶时的后备功率为：

式中：Pe为发动机输出功率；Pd为汽车行驶阻力功率；Pei为转动惯量引起的功率；ηcvt为无级变速传动的传动效率；η0为主减速器的传动效率。

由此可知，由转动惯量消耗的功率最大值为：

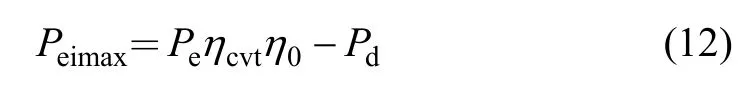
即

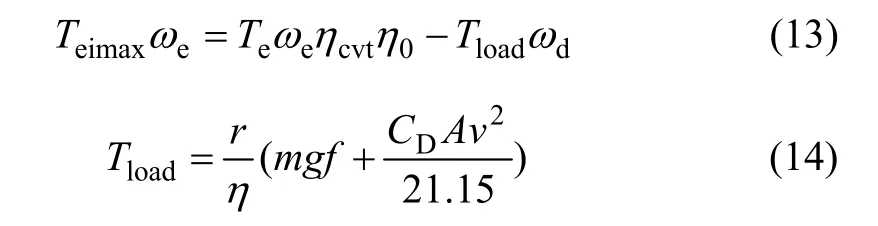
式中：m为汽车质量；g为重力加速度；f为滚动阻力系数；CD为空气阻力系数；A为迎风面积；η为驱动轴的传动效率；Teimax为转动惯量引起的最大功率；ωe为发动机输出轴转速。

将式(14)和(15)代入式(13)得：

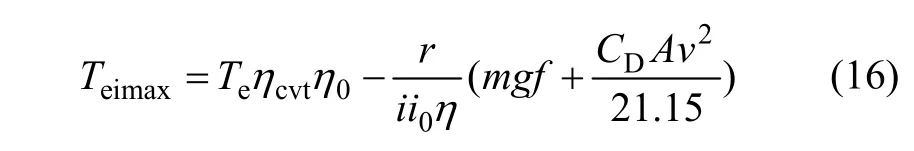
令

可得最大速比变化率为：

从式(17)可知，不同的运动状态最大速比变化率不同，最大速比变化率与发动机角速度成反比，同一发动机输出转矩下，车速越高最大速比变化率越低。

3.2 汽车加速时的仿真

为了验证无级变速系统速比控制策略，仿真研究了车辆在等速行驶时加速过程的动态响应，不考虑汽车起步时的状态。

图8所示为假设最大速比变化率为2，初始车速保持在90 km/h，并在10 s时急加速下，采用常规控制方法与速比变化率控制方法时汽车加速的动态特性。由仿真结果可知，常规控制下，加速度先急速下降到-1.82 m/s2，再迅速增大，汽车出现减速现象，此时速比变化率对汽车产生负的加速作用效果。考虑了汽车的速比变化率影响因素后，加速度不会出现负值，而且加速度迅速增大，此时的车速平稳增大，不会出现减速现象。在2种不同的控制方法下车速达到100 km/h时所需要的时间分别为3.208 s和3.107 s。由此可知：采用速比变化率控制方法能有效消除汽车的负加速现象，使汽车加速过程中的平顺性得到明显改善，且能够改善汽车加速时的加速响应。

图 9(a)所示为在考虑了后备功率的限制因素后，汽车在加速时，不同的车速和速比运行工况下理想的最大速比变化率的模型。由于在实际使用情况下，速比变化率一般为(-2，2)[14-16]，则汽车加速时实际的最大速比变化率如图9(b)所示。以此来控制CVT速比变化率就能消除汽车加速时的负加速现象。

3.3 汽车减速时的仿真

图10所示为假设最大速比变化率为2，车速保持在120 km/h，并在10 s时急减速下，采用常规控制方法与速比变化率控制方法时汽车急减速的动态特性。由仿真结果可知，在常规控制下，加速度先急速上升到1.39 m/s2，再迅速减小，汽车出现加速现象，此时速比变化率对汽车产生负的减速作用效果。考虑了汽车的速比变化率影响因素后进行的速比控制，减速度不会出现正值，而且减速度迅速减小到最小值，此时，车速平稳降低，不会出现加速现象。在2种控制方法下车速降到100 km/h时所需要的时间分别为7.594 s和6.275 s。由此可知：采用速比变化率控制方法能有效消除汽车的负减速现象，使汽车减速过程中的平顺性得到明显改善，且能够改善汽车减速时的动态响应。

图11(a)所示为在考虑了后备功率的限制因素后，汽车在减速时不同的车速和速比运行工况下理想的最小速比变化率。而汽车减速时，受CVT液压系统工作能力的限制，实际的速比变化率的绝对值通常不超过2，修正后的不同车速和速比运行工况下实际的最小速比变化率如图11(b)所示。

图8 不同控制方法下汽车加速时动态特性的仿真结果Fig.8 Simulation results of acceleration dynamic characteristics by different control methods

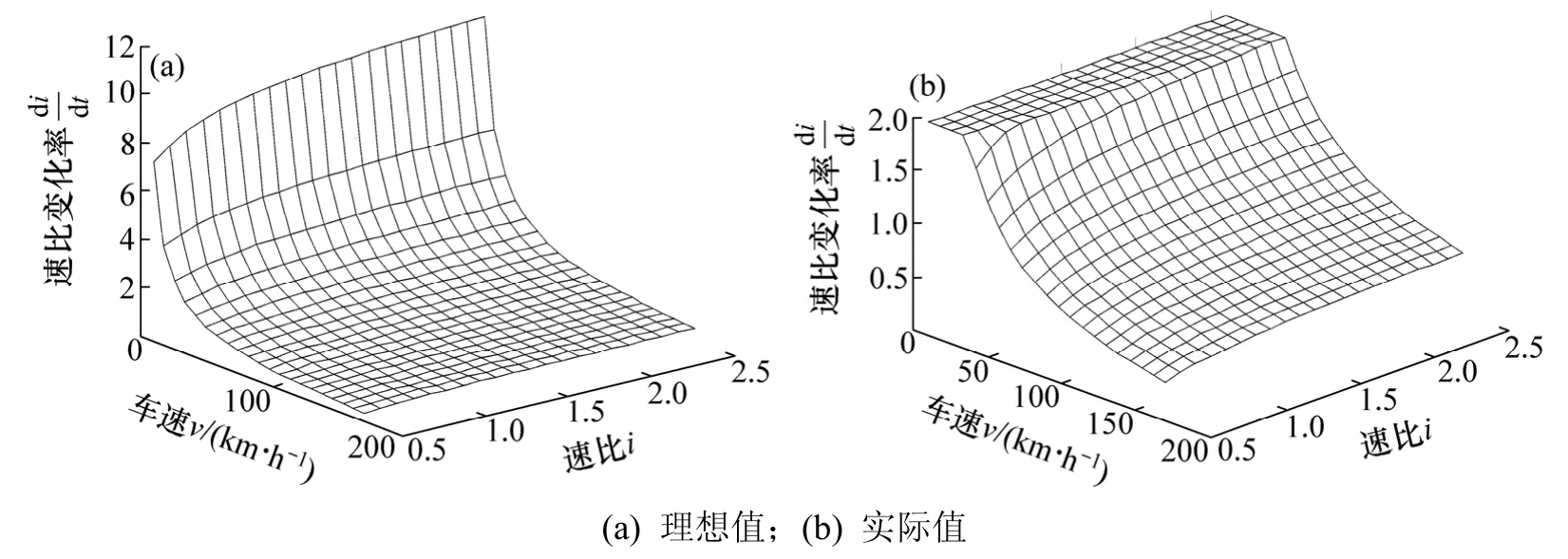
图9 汽车加速工况下的最大速比变化率Fig.9 Maximum ratio changing rate during vehicle acceleration

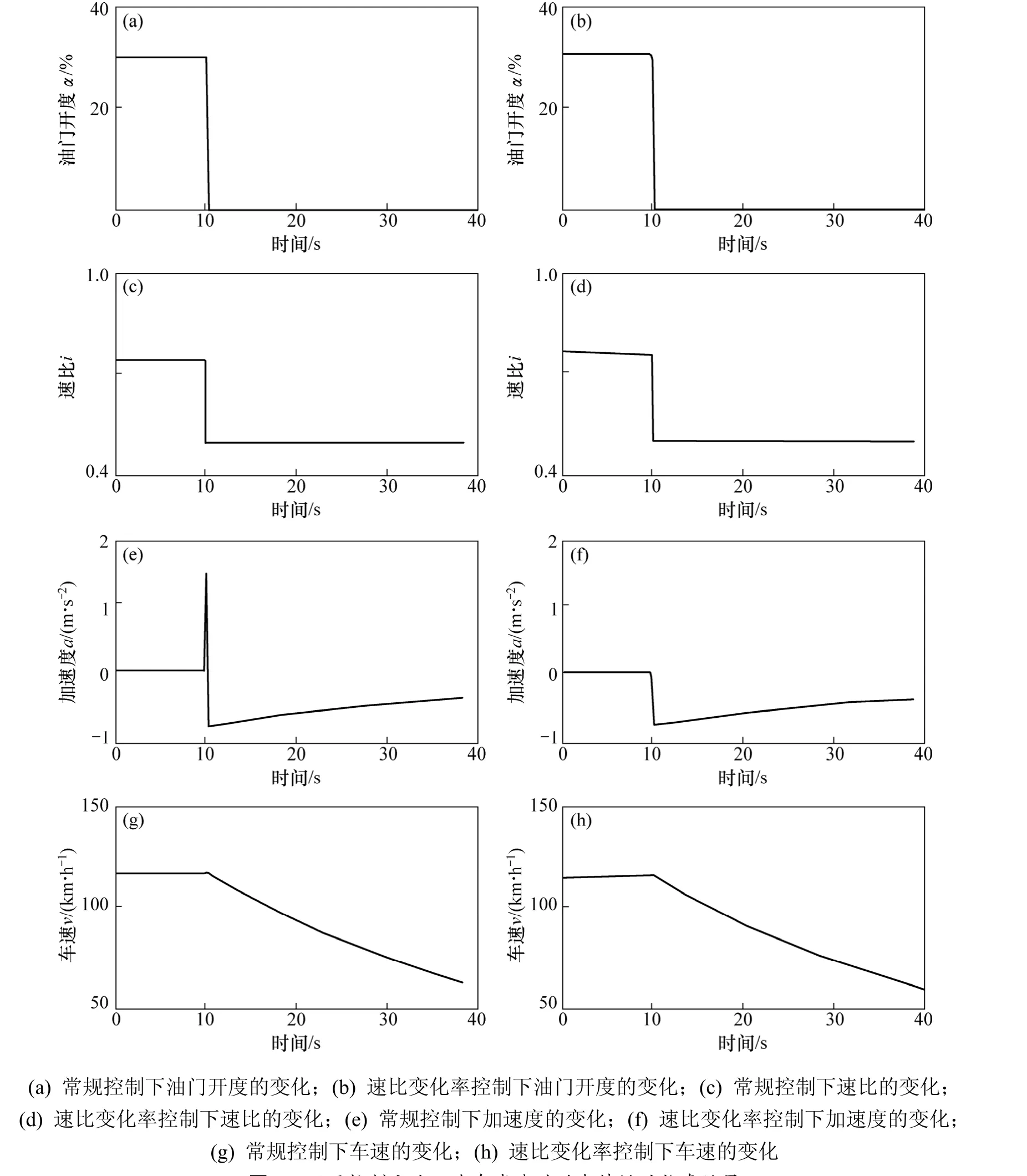
图10 不同控制方法下汽车减速时动态特性的仿真结果Fig.10 Simulation results of deceleration dynamic characteristics by different control method

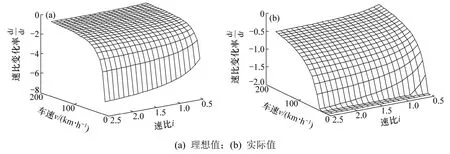
图11 汽车减速工况下的最小速比变化率Fig.11 Minimum ratio changing rate during vehicle deceleration

4 结论

(1) 在对无级变速传动系统动力学分析的基础上，综合考虑了后备功率对速比变化率的限制因素，得出最大或最小速比变化率的计算公式。

(2) 采用速比变化率控制方法能有效消除汽车的负加、减速现象，使汽车加、减速过程中的平顺性得到明显改善，且能够改善汽车加、减速时的响应速度。

(3) 根据仿真结果，得出汽车加减速时各工况下理想的速比变化率，在考虑液压系统对速比变化率影响的基础上，得到汽车加减速时各工况下实际的速比变化率。

[1] Rondinelli A, Baldissera P, Delprete C. Design, Construction and Experimental Testing of an High Efficiency Continuously Variable Transmission[C]//SAE. Detroit, 2009-01-1542.

[2] YANG Xin-hua. Electro-Mechanical Control Devices for Continuously Variable Transmission of Vehicle[C]//SAE. Detroit,2008-01-1687.

[3] 谢先平, 温嘉斌, 周美兰, 等. 金属带式汽车无级变速系统建模及动态仿真分析[J]. 电机与控制学报, 2005, 9(1): 72-76.XIE Xian-ping, WEN Jia-bin, ZHOU Mei-lan, et al. Modeling and dynamic simulation of mental v-belt continuously variable transmission system[J]. Electric Machines and Control, 2005,9(1): 72-76.

[4] 薛殿伦, 陈伟生, 冯显武. 金属带式无级变速器速比匹配与控制研究[J]. 中国公路学报, 2009, 22(2): 116-121.XUE Dian-lun, CHEN Wei-sheng, FENG Xian-wu. Study of speed ratio match and control of melt belt CVT[J]. China Journal of Highway and Transpor, 2009, 22(2): 116-121.

[5] Lee H, Kim H. Improvement in fuel economy for a parallel hybrid electric vehicle by continuously variable transmission ratio control[J]. Automobile Engineering, 2005, 219(1): 43-51.

[6] 何仁, 马承广, 张涌, 等. 基于驾驶意图的无级变速器目标速比确定方法[J]. 农业机械学报, 2009, 40(5): 16-19.HE Ren, MA Cheng-guang, ZHANG Yong, et al. Method to determine target speed ratio of CVT based on driving intention[J]. Transactions of the Chinese Society for Agricultural Machinery, 2009, 40(5): 16-19.

[7] 于峰, 卢伟. 金属带式无级变速传动系统综合控制策略的研究[J]. 佳木斯大学学报, 2008, 26(3): 304-307.YU Feng, LU Wei. Study on comprehensive controlling strategy of metal continuously variable transmission[J]. Journal of Jiamusi University, 2008, 26(3): 304-307.

[8] 何仁, 夏晶晶, 张涌, 等. 基于滞后特性的无级变速器速比控制策略[J]. 中国机械工程, 2009, 20(12): 1403-1407.HE Ren, XIA Jing-jing, ZHANG Yong, et al. Ratio control strategy of CVT on lagging characteristics[J]. China Mechanical Engineering, 2009, 20(12): 1403-1407.

[9] 胡建军, 秦大同, 舒红. 金属带式无级变速传动系统速比匹配控制策略[J]. 重庆大学学报, 2001, 24(6): 12-17.HU Jian-jun, QIN Da-tong, SHU Hong. Speed ratio matching strategies of metal V-belt type CVT system[J]. Journal of Chongqing University, 2001, 24(6): 12-17.

[10] Unno T, Sakaue M, Ishioka K, et al. Development of electronically controlled CVT focusing on Rider's intention of acceleration and deceleration[C]//SAE. Detroit, 2007-32-0011.

[11] Bonsen B, Steinbuch M, Veenhuizen P A. CVT ratio control strategy optimization[C]//2005 IEEE Conference on Vehicle Power and Propulsion. Chicago, 2005: 227-231.

[12] Jerzy J. Control of the transmission ratio derivative in passenger car power train with CVT[C]//SAE, Detroit, 2001-01-1159.

[13] Gallegos J A, Cruz Villar C A, Portilla Flores E A. Parametric optimal design of a pinion-rack based continuously variable transmission[C]//Proceedings of the 2005 IEEE/ASME International Conference on Advanced Intelligent Mechatronics.Monterey, 2005: 899-904.

[14] Togai K, Koso M. Dynamic scheduling control for engine and gear shifts: Consolidation of fuel-economy optimization and reserve power[J]. Mitsubishi Motors Technical Review, 2006(18):24-31.

[15] 孙冬野, 秦大同, 汪新国. 无级变速传动系统速比变化率的设计方法[J]. 汽车工程, 2006, 28(10): 910-913.SUN Dong-ye, QIN Da-tong, WANG Xin-guo. Design method of ratio changing rate of continuously variable transmission system[J]. Automotive Engineering, 2006, 28(10): 910-913.

[16] 汪新国. 金属带式无级变速传动液压控制系统设计方法研究[D]. 重庆: 重庆大学机械工程学院, 2005: 32-35.WANG Xin-guo. Study on design method of metal V-belt CVT hydraulic system[D]. Chongqing: Chongqing University. College of Mechanical Engineering, 2005: 32-35.