连退炉内炉辊热变形对带钢瓢曲变形的影响

唐荻，杨静，苏岚，江海涛，杨荃

(北京科技大学 高效轧制国家工程研究中心，北京，100083)

连续退火机组将冷轧带钢的清洗、退火、平整、精整等工艺集于一体，与传统的罩式炉退火工序相比，具有生产周期短、布置紧凑、便于生产管理、劳动生产率高以及产品质量优异等优点。其中，连续退火炉是连续退火机组的重要组成部分。根据工艺要求，连续退火炉可分为预热段、加热段、均热段、缓冷段、快冷段、时效段和终冷段等炉段。带钢依靠炉辊驱动在炉内各个区域运行时，常会发生瓢曲变形，严重影响了生产的稳定性。连退炉内带钢瓢曲变形实质上是薄板的屈曲和后屈曲变形[1-4]，已有文献分别通过实验[5-7]、解析法[8-9]和有限元法[9-12]等方法对带钢瓢曲变形进行了研究。但目前国内外研究带钢瓢曲变形时，很少考虑炉辊的热变形，大多采用固定辊形进行研究[10-12]。实际生产中，带钢在连退炉内运行时，由于炉辊局部与带钢接触，使得炉辊温度沿辊身方向分布不均匀，最终会发生形状变化。相关研究[7-8]表明：炉辊形状对带钢瓢曲变形影响很大，因此研究炉辊热变形对带钢瓢曲变形的影响是十分必要的。由于连退炉结构的封闭性和复杂性，使得实验法和解析法存在一定局限性，因此，本文作者以某厂连续退火炉为研究对象，通过有限元计算方法研究了炉辊热变形对带钢瓢曲变形的影响，旨在为选择合适的炉辊和改善连退炉内带钢瓢曲变形提供理论依据。

1 有限元仿真

在连退炉的加热段和快冷段，带温和炉温差别大，炉辊热变形明显，因此，本文选择加热段和快冷段的炉辊和带钢为研究对象。并根据现场工艺规定，选择加热段炉温为 820 ℃，张力为 7 kN，快冷段炉温为400 ℃，张力为11 kN。

1.1 几何模型及边界条件

本文分别建立限元模型，对炉辊热变形和带钢屈曲变形进行计算。

实际生产中，炉辊在连退炉内的转速达200 m/min以上。当炉辊转动时间较长时，可以忽略炉辊沿周向和径向的温差，只需考虑辊身温度分布不均引起的炉辊热变形。采用如图1所示的轴对称模型计算炉辊的热变形。炉辊初始辊形为单锥度辊，其形状如图 2所示。

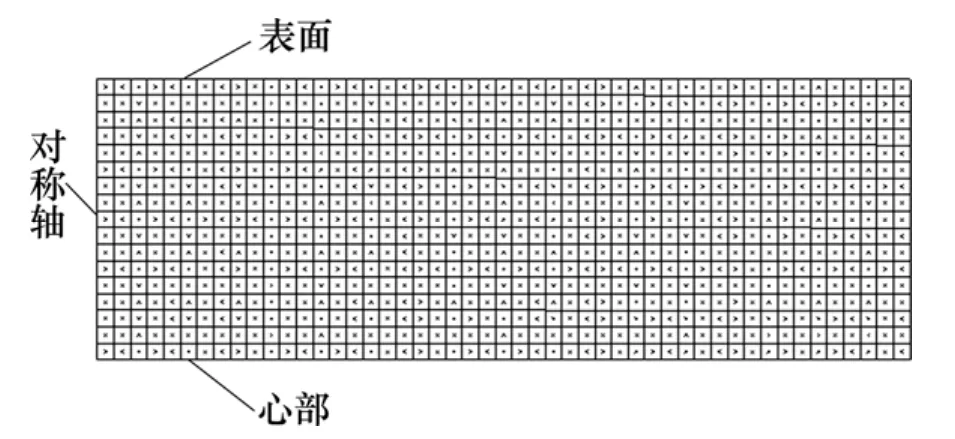
图1 计算炉辊热变形的有限元模型Fig.1 FEM model for roller thermal deformation

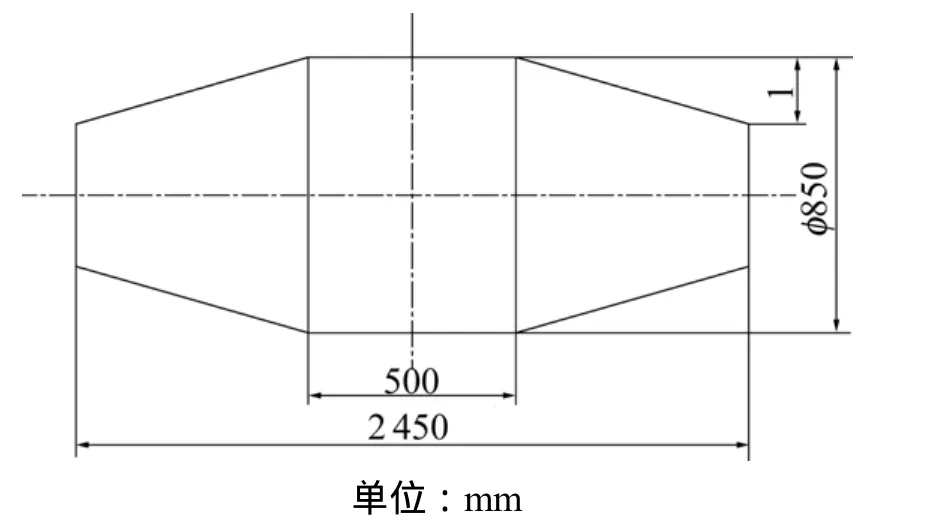
图2 炉辊的初始形状和尺寸Fig.2 Original shape and dimension of roller

分别采用热变形前后的炉辊形状对带钢进行屈曲计算，考虑到连退炉内的空间对称性和周期性，建立如图3所示的有限元模型进行屈曲分析。其中，带钢为冷轧后的平板带钢，带宽为1 600 mm，带厚为0.8 mm。选用四边形薄壳单元作为带钢单元，带钢两截断边位于上下炉辊的中间位置，如图4所示。对带钢进行屈曲分析时，炉辊固定不动，在带钢纵向对称线的节点上施加横向对称约束，将张应力P分步加载到带钢两截断边上，如图4所示。

图3 带钢屈曲分析的有限元模型Fig.3 FEM model for strip buckling analysis

图4 计算模型的示意图Fig.4 Schematic diagram of model

1.2 材料模型

假设炉辊热膨胀系数不随温度改变，其值为1.7×10-5/℃[13]，带钢泊松比ν=0.3。采用文献[14-15]中的连续退火炉内带钢力学性能表达式：

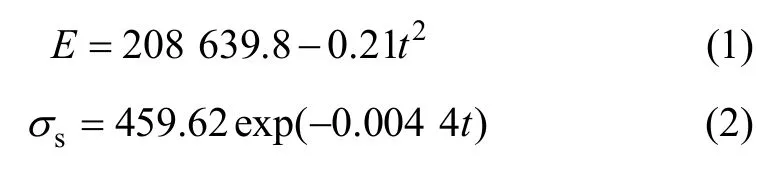
式中：E为弹性模量，MPa；σs为屈服强度，MPa；t为带温，℃。

1.3 计算工况

炉辊的热变形计算时，采用文献[8]给出的炉辊温度分布曲线，如图5所示，其中炉辊温差为炉温和带温之差。并根据炉辊温度分布，编制相应的子程序将温度分步加载到炉辊上，而后通过热应力计算得到炉辊热变形后的形状。为了研究炉辊温差对炉辊热变形的影响，在加热段和快冷段分别采用不同的带温进行计算，计算工况如表1所示。

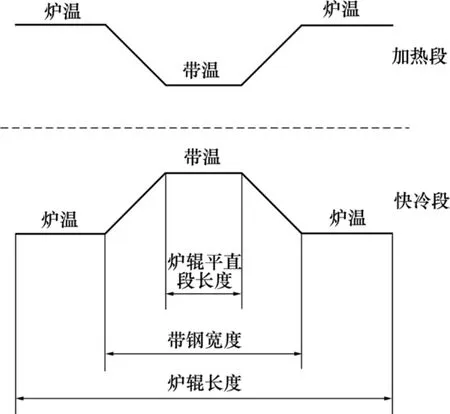
图5 炉辊温度分布曲线Fig.5 Distribution of roller temperature

表1 炉辊温度的选择Table 1 Choice of roller temperature ℃

提取炉辊热变形后的母线形状并绕辊轴旋转生成刚性面，作为炉辊热变形后的辊形，而后分别采用热变形前和热变形后的炉辊对带钢进行屈曲分析。由于屈曲计算过程中涉及到几何非线性和边界条件非线性，本文采用MARC软件提供的非线性屈曲分析的方法进行屈曲计算。将张应力分步加载到带钢上，通过提取特征值计算临界屈曲应力。

2 计算结果与分析

2.1 炉辊热变形的计算结果与分析

2.1.1 炉辊温差对炉辊形状的影响

炉辊的初始形状如图6所示，图7和图8所示分别为在加热段和快冷段对应于不同带温的炉辊温度分布曲线。由于炉辊温度分布不均匀，炉辊热变形后，其形状将发生改变，如图9和图10所示。从图9～10可见：在加热段和快冷段，炉辊热变形后其直径都有所增加，加热段炉辊直径始终大于快冷段炉辊直径；加热段，炉辊温差约以 80 ℃为界，当炉辊温差小于80 ℃时，炉辊热变形后为双锥度辊，炉辊平直段长度保持不变；当温差为80 ℃时，炉辊热变形后接近于单锥度辊，其炉辊平直段长度增大；当温差大于80 ℃时，随着温差的增大，炉辊将变为类似于“M”型辊。在快冷段，炉辊存在温差时，炉辊热变形后为双锥度辊。

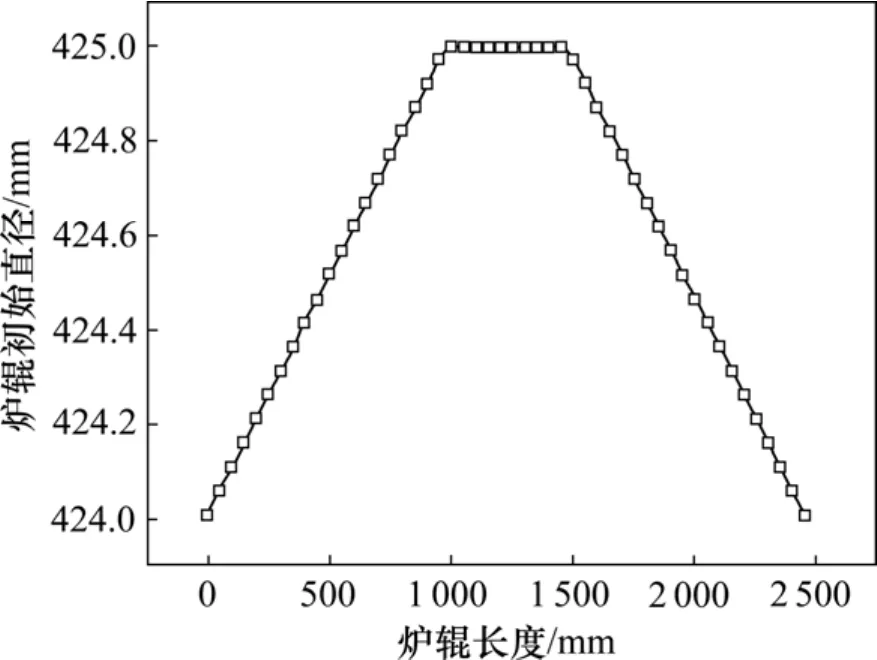
图6 炉辊初始形状Fig.6 Shape of original roller

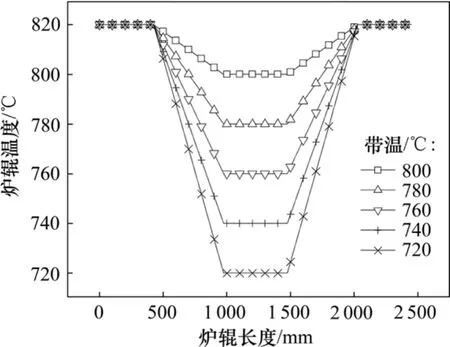
图7 加热段炉辊温度分布Fig.7 Temperature distribution of roller in heating section

图8 快冷段炉辊温度分布Fig.8 Temperature distribution of roller in rapid cooling section

图9 加热段炉辊热变形后的形状Fig.9 Shape of roller after thermal deformation in heating section

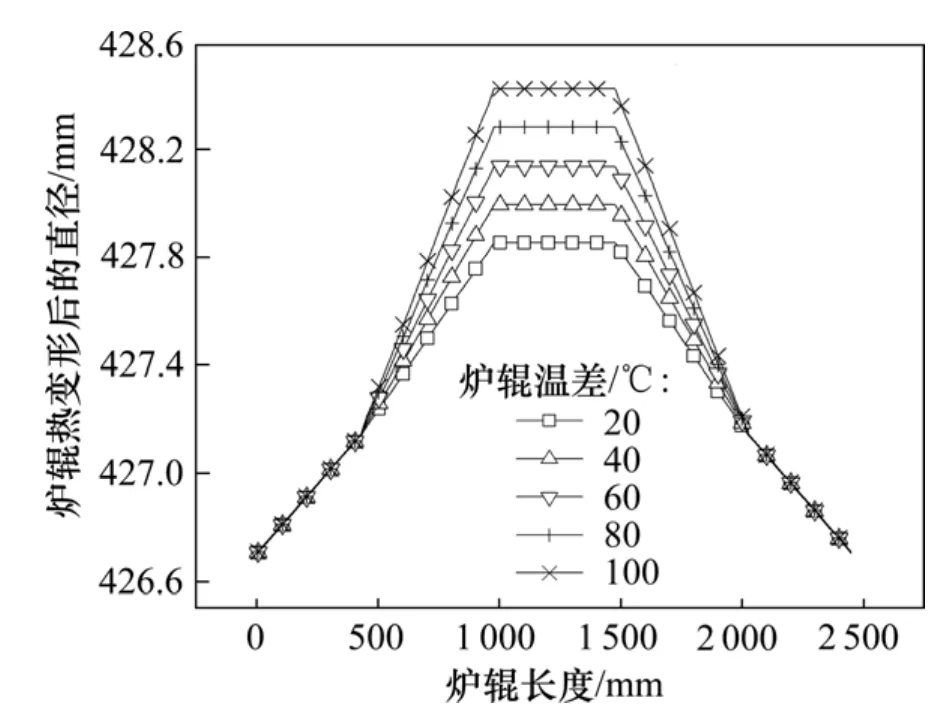
图10 快冷段炉辊热变形后的形状Fig.10 Shape of roller after thermal deformation in rapid cooling section

2.1.2 炉辊温差对炉辊总锥度的影响

分析了加热段和快冷段炉辊热变形后的总锥度，结果如表2和表3所示。其中，正值表示正锥度，负值表示负锥度。图11(a)所示为在加热段，炉辊热变形后总锥度随炉辊温差的变化趋势：当炉辊温差小于80 ℃时，炉辊热变形后总锥度随温差的增大线性降低，平均单位温差总锥度的变化量为 7.1×10-3mm/℃；当炉辊温差达到80 ℃时，炉辊热变形后总锥度降低到初始锥度的 44.4%；温差在 80～100 ℃之间时，炉辊热变形后总锥度变化最剧烈，由正锥度变为负锥度，平均单位温差总锥度的变化量为 3.7×10-2mm/℃。图11(b)所示为在快冷段，炉辊热变形后总锥度与炉辊温差的关系：炉辊热变形后总锥度随温差呈线性增加关系，平均单位温差总锥度的变化量为7.1×10-3mm/℃，温差达到100 ℃时，炉辊热变形后总锥度比初始锥度增加了71.3%。

表2 加热段炉辊热变形后的总锥度Table 2 Total taper of roller after thermal deformation in heating section

表3 快冷段炉辊热变形后的总锥度Table 3 Total taper of roller after thermal deformation in rapid cooling section

图11 炉辊热变形后的总锥度随炉辊温差变化Fig.11 Total taper of roller after thermal deformation with increasing roller temperature difference

2.2 炉辊热变形对带钢临界屈曲应力的影响

图12和图13分别所示为加热段和快冷段炉辊温差为60 ℃时，炉辊热变形前后，计算得到的带钢屈曲模态。表4和表5给出了带钢临界屈曲应力的计算结果。可以看出：在加热段，炉辊温差为80 ℃时，在给定工艺张应力(5.47 MPa)下带钢不会发生屈曲变形。当温差为100 ℃时，炉辊变成“M”型辊，本文对该辊形下带钢临界屈曲应力不做分析。在加热段，只分析温差在 80 ℃以内的炉辊热变形对带钢临界屈曲应力的影响。

2.2.1 加热段带钢临界屈曲应力

图14所示为在加热段，炉辊热变形前和热变形后得到带钢的临界屈曲应力与带温的关系。炉辊热变形前后，带钢临界屈曲应力都是随带温的增加而降低，并且，带温越高，带钢临界屈曲应力变化越平缓；受炉辊热变形的影响，炉辊热变形后带钢的临界屈曲应力要大于热变形前的值，并且带温越低，炉辊热变形后和热变形前的带钢临界屈曲应力值差值越大。

2.2.2 快冷段带钢临界屈曲应力

图15所示为在快冷段，炉辊热变形前和热变形后得到带钢的临界屈曲应力与带温的关系。对于同一带温，炉辊热变形前的带钢临界屈曲应力要大于炉辊热变形后的值；炉辊热变形前和热变形后带钢的临界屈曲应力都随着带温的增大而减少，并且带温越大，炉辊热变形前和热变形后的带钢临界屈曲应力差越大。

图12 加热段(820 ℃)炉辊温差为60 ℃时带钢的屈曲模态Fig.12 Strip buckling mode with roller temperature difference of 60 ℃ in heating section at 820 ℃

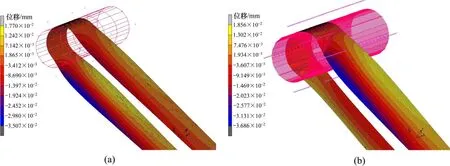
图13 快冷段(400 ℃)炉辊温差为60 ℃时带钢的屈曲模态Fig.13 Strip buckling mode with roller temperature difference of 60 ℃ in rapid cooling section at 400 ℃

表4 加热段带钢临界屈曲应力Table 4 Critical buckling stress of strip in heating section

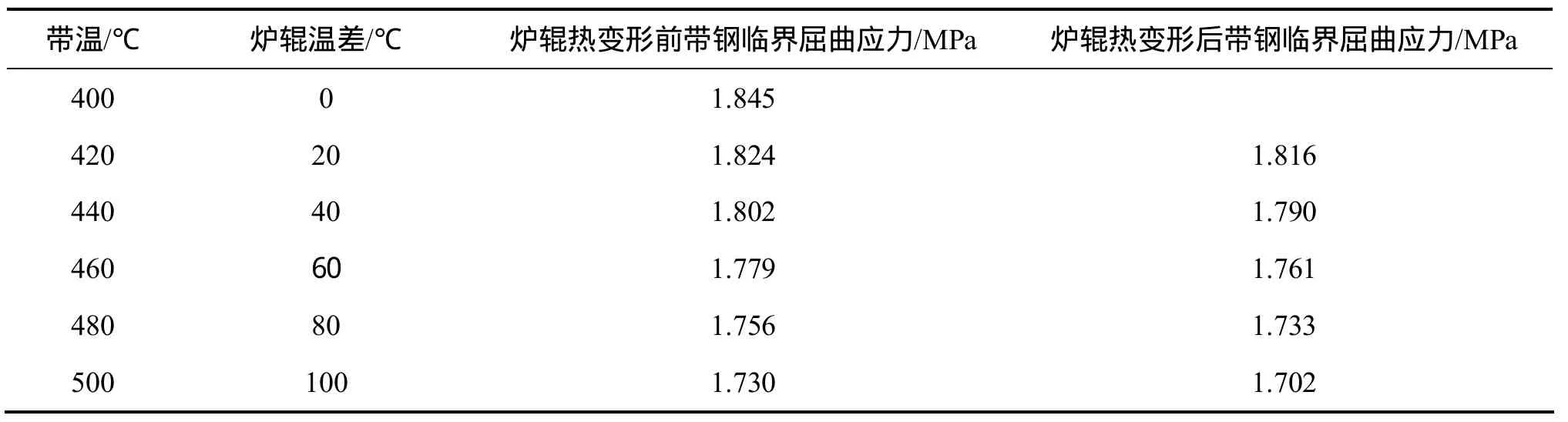
表5 快冷段带钢临界屈曲应力Table 5 Citical buckling stress of strip in rapid cooling section

2.3 炉辊温差的控制及炉辊的选择

2.3.1 加热段

在加热段(820 ℃)，当炉辊温差大于80 ℃时，炉辊热变形后为“M”型辊，炉辊总锥度为负锥度。在实际生产中，“M”型辊和负锥度辊形对防止带钢瓢曲和跑偏都是不利的。应该采取相应措施，将炉辊温差控制在80 ℃以内，此时，炉辊一定程度的热变形可以抑制带钢的瓢曲变形。由此可以推断：在连退炉加热段，可以选择初始锥度较大的炉辊，这样既能增大炉辊的纠偏能力，同时又因炉辊在炉内产生一定程度的热变形，减小了带钢瓢曲变形的可能性。

2.3.2 快冷段

在快冷段(400 ℃)，炉辊存在温差时，辊形变为双锥度辊，其总锥度将增大，导致带钢临界屈曲应力减小。并且温差越大，热变形后的总锥度越大，带钢临界屈曲应力越小。总锥度的增大提高了炉辊的纠偏能力，但也增大了带钢瓢曲的可能性。因此，应该控制快冷段炉辊温差，使其尽量小，并且为了抑制快冷段带钢的瓢曲变形，可以选择初始锥度较小的炉辊。

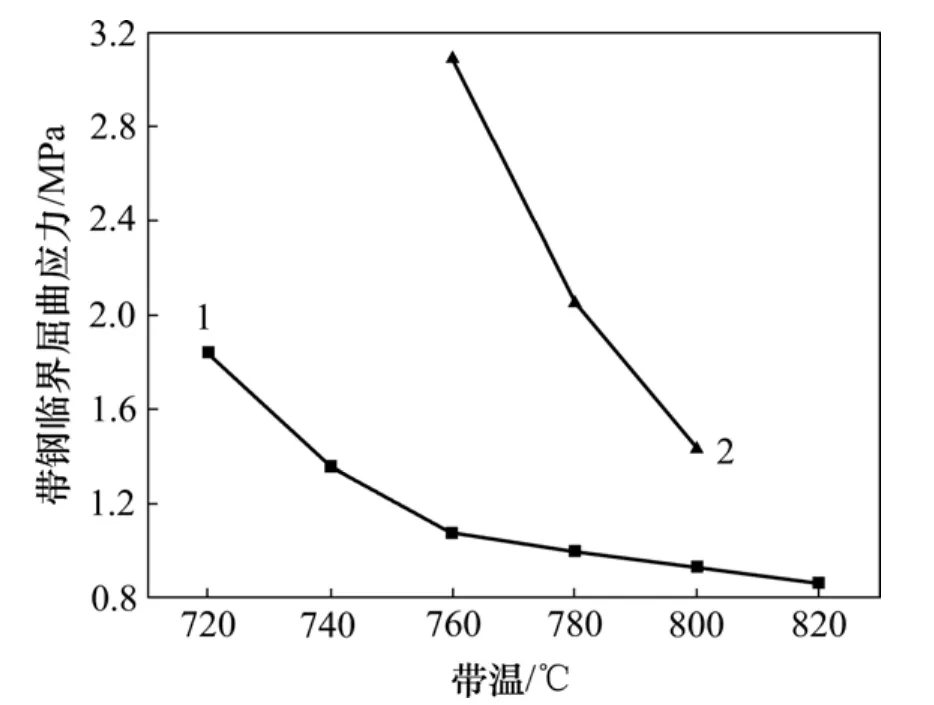
图14 加热段炉辊热变形前后不同带温条件下带钢临界屈曲应力Fig.14 Comparison of strip critical buckling stress with different strip temperature in heating section

图15 快冷段炉辊热变形前后不同带温条件下带钢临界屈曲应力Fig.15 Comparison of strip critical buckling stress with different strip temperature in rapid cooling section

3 结论

(1) 在加热段，当炉辊温差小于80 ℃时，炉辊热变形后为双锥度辊；当温差达到80 ℃时，炉辊近似为单锥度辊；当温差大于80 ℃时，炉辊热变形后为“M”型炉辊。在快冷段，当炉辊温度分布不均匀时，炉辊热变形后为双锥度辊。

(2) 在加热段，当炉辊存在温差时，炉辊热变形后总锥度减小。当炉辊温差小于80 ℃时，炉辊总锥度为正锥度，并且随温差的增大而减小；当温差为 80～100 ℃时，炉辊总锥度发生突变，由正锥度变为负锥度。在快冷段，当炉辊存在温差时，炉辊热变形后总锥度增大，并且炉辊总锥度随炉辊温差的增大而增大；当炉辊温差达到100 ℃时，炉辊总锥度较初始锥度增大了71.3%。

(3) 在加热段和快冷段，炉辊热变形前后，带钢的临界屈曲应力都是随带温升高而减小。在加热段，炉辊热变形后的带钢临界屈曲应力大于热变形前的值，并且随着带温的升高，炉辊热变形前后带钢临界屈曲应力差逐渐减小；在快冷段，炉辊热变形后的带钢临界屈曲应力小于热变形前的值，并且随着带温的升高，炉辊热变形前后计算的带钢临界屈曲应力差越大。

(4) 基于计算分析，从炉辊热变形角度考虑，对加热段和快冷段的炉辊的温差控制及炉辊选择给出了合理的建议：在连退炉加热段，可以选择初始锥度较大的炉辊，这样既能增大炉辊的纠偏能力，同时又因炉辊在炉内产生一定程度的热变形，减小了带钢瓢曲变形的可能性；应该控制快冷段炉辊温差，使其尽量小，并且为了抑制快冷段带钢的瓢曲变形，可以选择初始锥度较小的炉辊。

[1]Wang C M, Aung T M. Plastic buckling analysis of thick plates using p-Ritz method[J]. International Journal of Solids and Structures, 2007, 44(18/19): 6239-6255.

[2]Brighenti R. Numerical buckling analysis of compressed or tensioned cracked thin plates[J]. Engineering Structures, 2005,27(2): 265-276.

[3]Kim S E. Thai H T, Lee J. Buckling analysis of plates using the two variable refined plate theory[J]. Thin-Walled Structures,2009, 47(4): 455-462.

[4]Rahai A R. Alinia M M, Kazemi S. Buckling analysis of stepped plates using modified buckling mode shapes[J]. Thin-Walled Structures, 2008, 46(5): 484-493.

[5]Kaseda Y. Control of flatness defects and warp in processing plant[J]. CAMP-ISIJ, 1992, 5(5): 1463-1466

[6]Kaseda Y. Control of buckling and crossbow in strip processing lines[J]. Iron and Steel Engineer, 1994, 9(9): 14-20.

[7]Matoba T. Effect of roll crown on heat buckling in continuous annealing and processing lines[J]. Iron and Steel, 1994, 80(8):61-66.

[8]Hu G K. Control of thermal crown in the roller inside the continuous annealing furnace[J]. Baosteel Technical Research,2009, 3(1): 51-55.

[9]戴江波. 冷轧宽带钢连续退火生产线上瓢曲变形的研究[D].北京: 北京科技大学机械工程学院, 2005: 32-73.DAI Jiang-bo. Study on the Strip Buckling in Continuous Annealing Production Line[D]. Beijing: University of Science and Technology Beijing. School of Mechanical Engineering,2005: 32-73.

[10]Sasaki T. Control of strip buckling and snaking in continuous annealing furnace[J]. Kawasaki Steel Technical Report, 1984,16(1): 37-45.

[11]Jacques N, Elias A, Potier-Ferry M, et al. Buckling and wrinkling during strip convey in processing lines[J]. Journal of Materials Processing Technology, 2007, 190(1/2/3): 33-40.

[12]Dai J B, Zhang Q D, Chang T Z. FEM analysis of large thermo-deflection of strips being processed in a continuous annealing furnace[J]. Journal of University of Science and Technology Beijing, 2007, 14(6): 580-584.

[13]Dietsch H. Roller for metal strip transfer in a continuous annealing furnace: US, 6709372 B2[P]. 2004-03-23.

[14]孙中建, 李胜袛, 林大为. CAPL炉内带钢张力分布研究[J].华东冶金学院学报, 1994, 11(2): 130-138.SUN Zhong-jian, LI Sheng-di, LIN Da-wei. The distribution of strip tension in the furnace of CAPL[J]. Journal of East China Institute of Metallurgy, 1994, 11(2): 130-138.

[15]许永贵, 陈守群, 孙中建. CAPL 炉内带钢热瓢曲机理的探究[J]. 华东冶金学院学报, 1994, 11(2): 1-6.XU Yong-gui, CHEN Shou-qun, SUN Zhong-jian. Study and discussion of the mechanism for the hot-waved surface of strip in the CAPL furnace[J]. Journal of East China Institute of Metallurgy, 1994, 11(2): 1-6.