SSDI体系非线性耦合阻尼比研究
夏栋舟,何益斌
(1. 长沙理工大学 土木与建筑学院,湖南 长沙,410114;2. 湖南大学 土木工程学院,湖南 长沙,410082)
土-结构动力相互作用(Soil-structure dynamic interaction,缩写为 SSDI)[1]是指由震源引起的地震波通过场地土的传播输入到结构体系使结构发生振动,同时,振动的结构产生惯性力如同新的震源又反过来作用于场地,引起新的场地振动再作用于结构体系。我国现行《建筑抗震设计规范》(GB 50011—2001)[2]仍然基于常阻尼比来研究建筑物的地震作用,没有考虑地基土、基础与上部结构动力相互作用而产生的阻尼耦合效应。因此,在传统的结构抗震设计中通常忽略由于土-结动力相互作用效应而导致地震作用减小的有利影响,这在一定程度上虽然保证了抗震设计的可靠度,但客观上又大大增加了工程投资,浪费了建设资源,对环境保护也有重大影响。因此,在建筑抗震设计中,应该对土-结构动力相互作用效应进行进一步研究,以便更好地指导工程设计,节约建设成本,而这其中一个最重要同时也是最复杂的问题是对SSDI体系阻尼性能的研究。在此,本文作者提出一种考虑基础质量和转动效应的改进简化计算模型,并通过对各个非线性参数的选取,推导出更能反映土-结构动力相互作用体系动力特性的非线性耦合阻尼比公式。通过实例与其他传统的阻尼比简化计算公式进行计算对比,以证明其有效性。
1 改进的SSDI体系非线性耦合阻尼比公式的提出
传统土-结构动力相互作用的简化计算方法具有代表性的有 Modify-Veletsos法(简称 MV 法)[3]、Modify-Bielak法(简称 MB法)[4]、ATC法[5]以及日本建筑学会地震荷载委员会推荐的 JAP法[1,6]。陈跃庆等[7]指出了这些方法的不足,并提出了改进的计算方法,但该方法仍然没有考虑上部结构在与土体及基础的动力相互作用时表现出的强非线性,且结构的阻尼比取为常值,未能考虑结构阻尼的非线性;同时,在地基阻抗和桩基阻抗计算中将土体假设为均匀土或土体模量随深度线性增加,不能充分考虑土体的非线性特性以及基础埋置深度的影响。
而在上、下部结构动力相互作用体系实际工作状态中,地震能量的损耗往往就发生在基础与地基土、基础与结构之间,这是彼此间非线性接触所致,因此,忽略基础质量的假设是不妥的。本文考虑基础质量为m0、基础的等效半径a,同时考虑柔性地基土本身的黏滞材料阻尼ξs,其简化计算模型如图1所示,建立体系的整体运动方程。
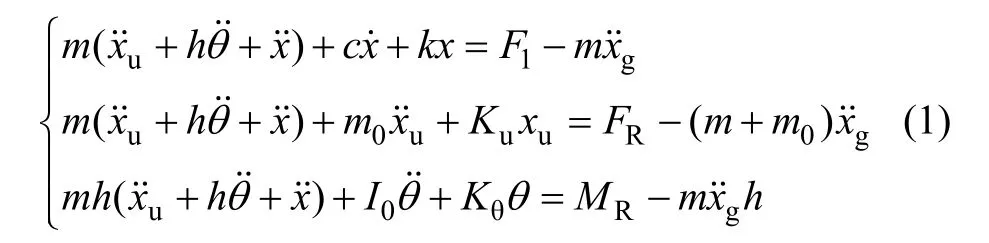
式中:F1为结构顶部承受的水平外力;FR与MR分别为基础承受的对应于外力作用的总作用力与总弯矩,在这里,FR=F1,MR=F1h;I0为基础与上部结构对各自通过质心的水平轴的惯性矩之和。
根据文献[8]中的计算方法进行推导,可得到方程的近似解:
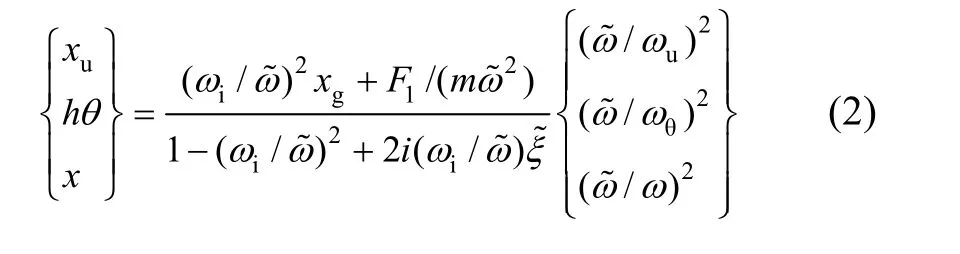
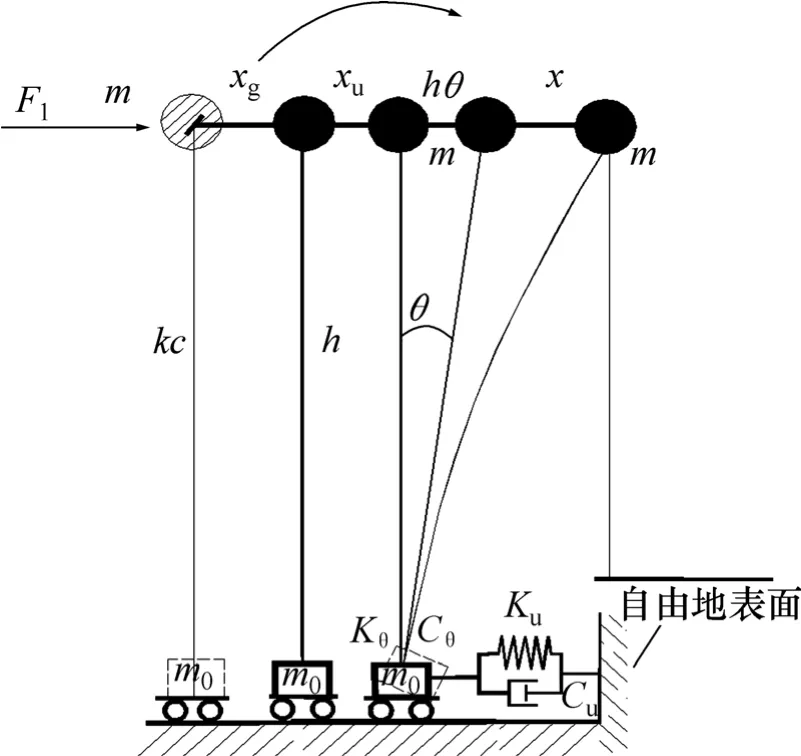
图1 土-结构动力相互作用体系简化计算模型Fig.1 Simplified calculation model for soil-structure-interaction system
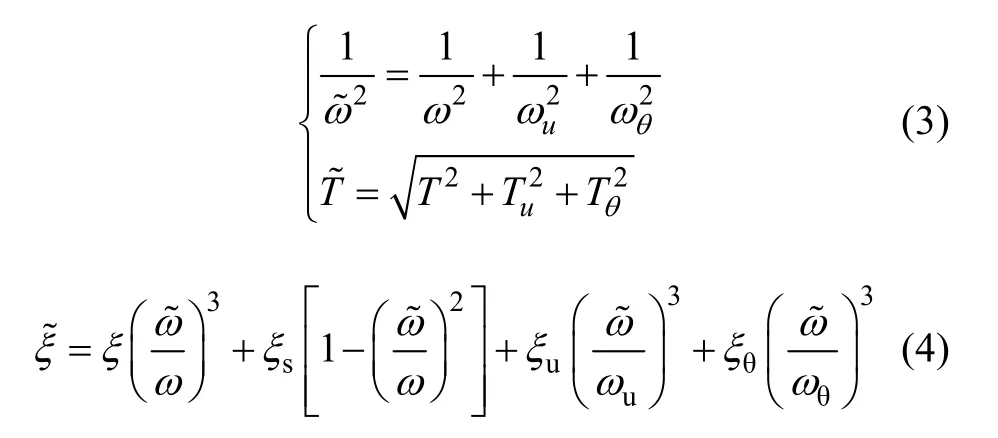
式中:ω和ξ分别为刚性地基上结构的自振频率与阻尼比;ωu和ωθ分别为地基基础平动与转动的特征频率;ξu和ξθ分别为地基基础平动与转动的辐射阻尼比;ξs为柔性地基的土介质黏滞材料阻尼。由于这些参数的取值均随不同上部结构性质、不同基础条件以及不同地基土性质的变化而呈非线性变化,由此得到的阻尼比是非线性耦合阻尼比。可以看出:式(3)和(4)不仅考虑了上部结构的阻尼特性,还考虑了地基在基础平动与转动情况下的辐射阻尼,同时也考虑了地基土的黏滞材料阻尼,能更加全面把握土-结构动力相互作用体系各部分的阻尼特性对整个体系阻尼的贡献。
2 土-结构动力相互作用体系非线性耦合阻尼比公式参数的选取与修正
本文提出的改进简化计算方法与传统的无质量计算模型相比有了较大改善,但由于该简化模型中考虑的是单质点体系,未考虑结构的非线性特性、基础形式、基础埋置深度、地基非均匀土层以及地基基础平动与转动耦合等因素的影响,因此,需要对公式中各项参数包括上部结构阻尼比ξ、自振频率ω、地基土材料阻尼ξs、基础平动和转动频率(ωu和ωθ)、基础平动和转动频率(ωu和ωθ)、基础平动和转动阻尼比(ξu和ξθ)等进行修正。
2.1 上部结构阻尼比ξ的修正
传统的几种简化计算方法对于上部结构阻尼比均基于常阻尼比为条件进行计算,上部结构的阻尼比通常选取常阻尼比ξ=0.05或ξ=0.02。但是,影响上部结构阻尼特性的因素非常多,不仅有结构外部的阻尼,而且包括结构内部的阻尼;同时,建筑材料、结构形式、结构变形等因素都对结构阻尼特性有重要影响,上部结构在考虑地基基础相互作用后,其阻尼特性表现出强烈的非线性,不能再以常阻尼比来进行动力计算,本文采用文献[9]中提出的基于结构层间广义相对剪切变形,针对不同结构形式的非线性阻尼比作为SSDI体系中上部结构阻尼比ξ,其具体计算公式如下。
对于框架填充墙结构:
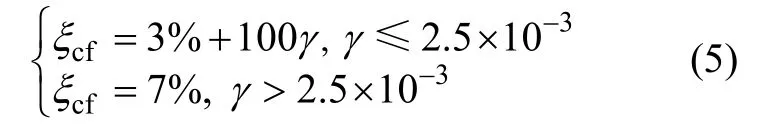
对于钢筋混凝土抗震墙结构:
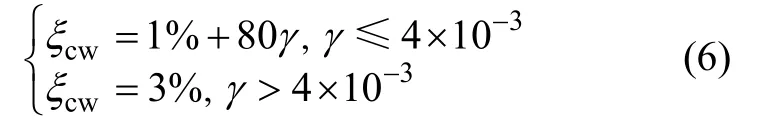
对于预制装配式结构:

对于空旷的框架-填充墙结构:
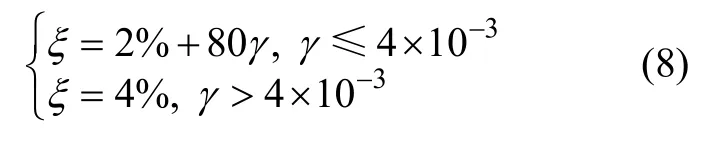
式中:γ为层间广义相对剪切变形,γ=xi/hi。层间广义相对剪切变形γ的取值也可根据规范[2]进行估算。
2.2 上部结构自振频率ω的计算
结构的自振频率是根据刚性地基假设条件进行计算的,ω可以根据通用计算公式得到:

刚性地基条件下上部结构的刚度k按照美国规范[5]中提供的公式进行计算:

式中:M为建筑物总质量;T为刚性地基时上部结构的周期。
2.3 地基土材料阻尼ξs的计算
目前国内外对土的研究非常广泛,但得到国际认可的是Hardin[10]对土的动剪切模量比与动剪应变幅值计算公式:
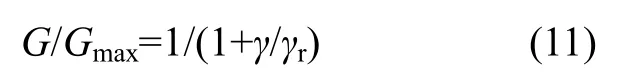
因此,阻尼比与动剪切模量比的关系式为:
式中:G和Gmax分别为土的动剪切模量与最大动剪切模量;γr为参考剪应变幅值;ξmax为最大阻尼比。
通常,土体材料阻尼的取值均是通过试验得到的。但在理论研究和应用中,如果没有试验资料作为地基土材料阻尼的取值依据,同时也没有详细的地勘资料来进行考证,那么,在实际计算中可以根据袁晓铭等[11]针对国内 10余个不同地区土样的试验结果推荐值进行取值,其不同土性的推荐阻尼比曲线如图2所示。在进行计算时,土体材料阻尼比的取值可以根据剪应变的不同在图中进行线性插值。
2.4 基础平动和转动频率ωu和ωθ的计算
根据文献[8]中式(4)~(7)可以得到ωu与ωθ的基本计算方法,其计算公式为:
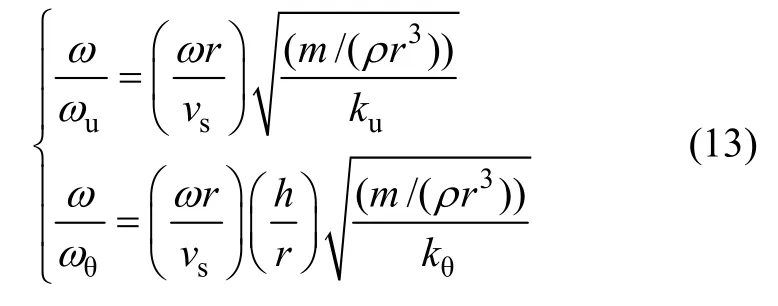
根据式(13),基础平动和转动频率ωu与ωθ的确定除了与基础有效半径r、土体剪切波速vs、无量纲频率比a0=ωr/vs、结构高度与基础半径的高径比h/r等因素有关外,需要重点关注基础平动、转动刚度ku与kθ的确定。
2.4.1ku与kθ基本确定方法
在已有的阻抗函数计算方法中,最广泛应用的是置于黏弹性半空间表面的圆形刚性基础的解,其中平动和转动弹簧阻尼器的实刚度为:

其中:αu和αθ为与频率相关的无量纲参数;Ku和K为半空间上基础的静刚度,其计算公式为:
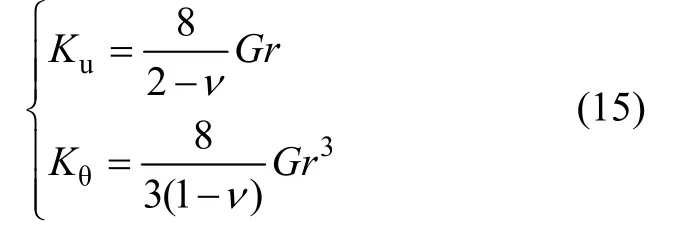
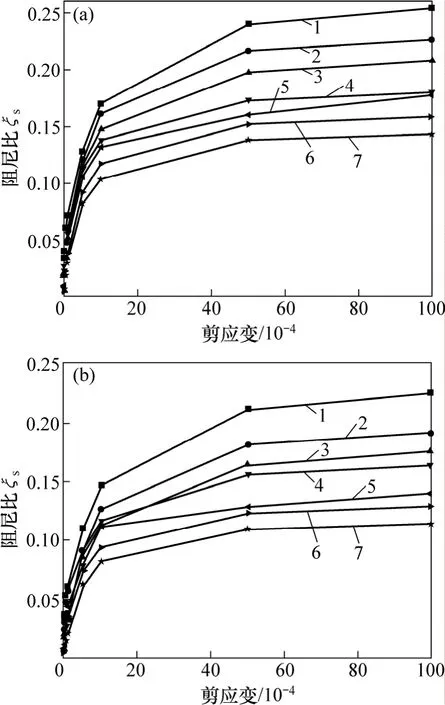
图2 常规土类材料阻尼比ξs推荐值示意图Fig.2 Recommended values for material damping ratio ξs of regular soil
式中:G为土的动剪切模量;ν为土的泊松比。
对于黏弹性土,引入土体的黏滞材料阻尼,αu和αθ的近似计算公式如下:
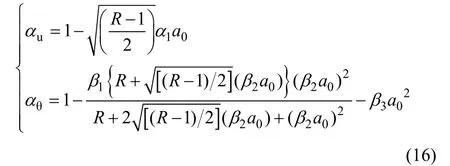
2.4.2ku与kθ在非均匀土层时的确定方法
地基土在实际地质条件下,其分布并不是单一的,也不是均匀的各向同性介质,通常其特征为:刚度随深度梯度增加或在相对较软的土层下有一层刚性很大的下卧层,这种非均匀土层情况下基础的静刚度可按下式进行近似计算:
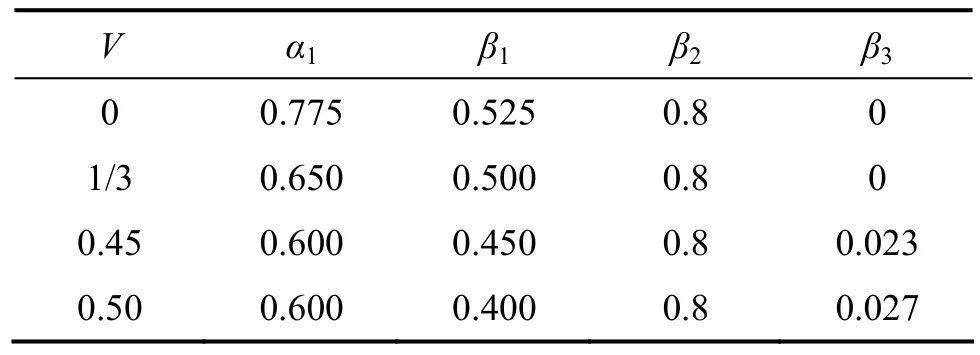
表1 系数 α1,β1,β2及 β3的取值Table 1 Values of α1, β1, β2 and β3
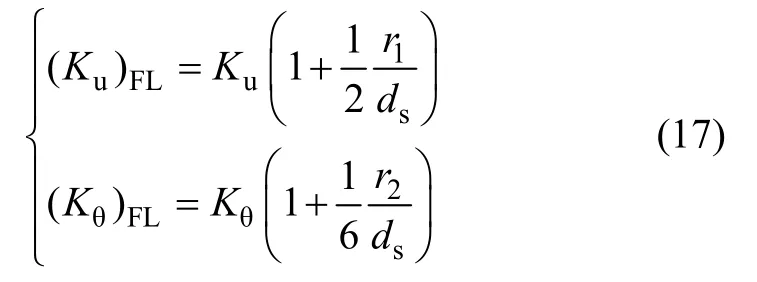
式中:(Ku)FL和(Kθ)分别为非均匀有限土层上基础的平动与转动静刚度;ds为土层厚度;r1和r2分别为按照面积(Af)和惯性矩(If)等效计算的基础半径。
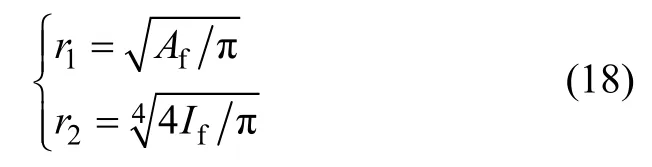
2.4.3ku与kθ在考虑基础埋深时的确定方法
Apsel等[12]经研究发现:基础的埋置情况对阻抗有很重要的影响。基于黏弹性半空间土介质为研究对象,考虑土体材料阻尼与辐射阻尼、基础质量、基础埋置深度等对土-基础体系阻抗的影响,同时还考虑基础平动与摆动的耦合作用,得到基础的静刚度计算公式为:
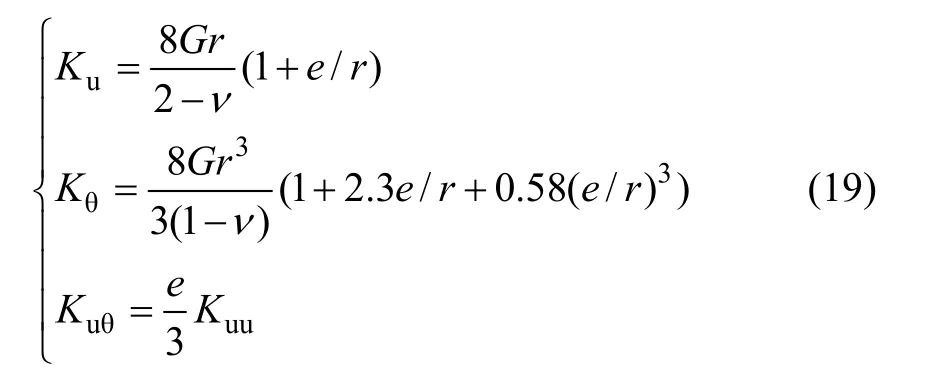
式中:G为地基土的动剪切模量;e/r为基础高度与基础有效半径的基础埋深比。
2.5 基础平动和转动阻尼比ξu和ξθ的计算
根据式(2)可以得到ξu与ξθ的基本计算方法,其计算公式为:
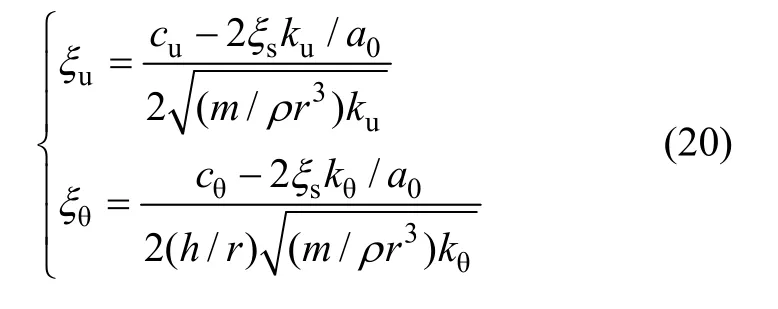
其中:ku与kθ的计算方法按照式(19)确定,这里关键是对cu与cθ进行确定。通过对阻抗的研究,平动和转动弹簧阻尼器的阻尼可以通过以下公式进行计算:
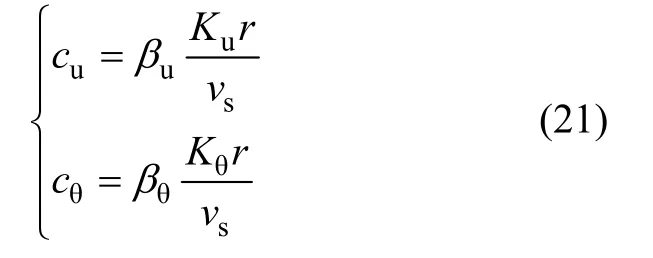
式中,vs为土的剪切波速;r为基础的有效半径;βu和βθ的近似计算公式为:
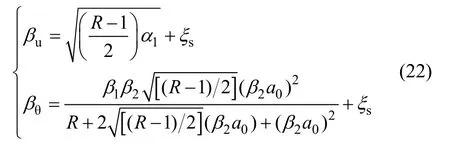
式中各参数取值同样根据表1进行选取,因此,cu与cθ的取值与基础的静刚度Ku和Kθ相关。
为了研究基础平动和转动阻尼比ξu和ξθ在不同地基条件下的取值,需要对基础平动和转动刚度ku与kθ、基础的平动和转动弹簧阻尼器的阻尼cu与cθ进行分析。在非均匀土层和不同基础埋深条件下,可以通过对基础静刚度Ku和Kθ的计算调整来考察不同地基条件下ξu与ξθ的取值。
3 非线性耦合阻尼比公式实例计算对比
为了验证论文提出的计算模型和非线性耦合阻尼比公式的合理性与可靠性,下面对同济大学的结构与地基相互作用振动台进行试验,对不同工况条件下体系的动力特性指标进行计算,同时与MV法、MB法、ATC法、日本建筑学会的JAP法以及文献[7]提出的简化计算法在同等试验条件下的计算结果进行对比。
试验条件如下:非均匀分层地基土条件,上部结构为12的层框架结构,输入白噪声和El-Centro地震波。其土-结构动力相互作用试验内容及模型比如表2所示,模型示意图及概况如图3和表3所示,模型各部分计算参数以及频率和阻尼比计算结果对比如表4~6所示。
通过表5和表6中各种简化计算方法的计算结果与试验实测结构进行对比分析得知:MV法、MB法、ATC法以及JAP法对土-结构动力相互作用体系频率和阻尼比的计算结果与实测值相比均有较大误差。总的来说,JAP法对阻尼的计算偏小而对频率的估算则相应偏大,另外3种方法其计算值与实测值相比并无规律。与这4种简化计算方法相比,文献[7]提出的简化计算法对实例的计算结果则表现出较高的精度,其基本误差控制在20%~50%,出现此种误差可能是没有考虑基础质量以及各部分阻尼性能耦合。经过对比分析,本文计算方法通过对已有简化方法的改进,对实例的计算结果与其他简化计算法的计算结果相比更接近于实测结果,相对误差控制在10%~20%。该误差的产生与结构及土体材料阻尼比的计算有关,同时也与试验实测数据本身的误差有一定关系。总之,采用本文方法对土-结构动力相互作用体系动力特性参数进行计算所得结果更接近实测值。
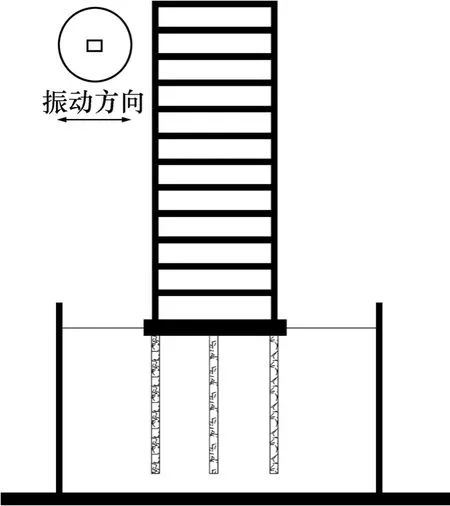
图3 框架结构SSDI体系示意图Fig.3 Diagram of SSDI system for frame construction
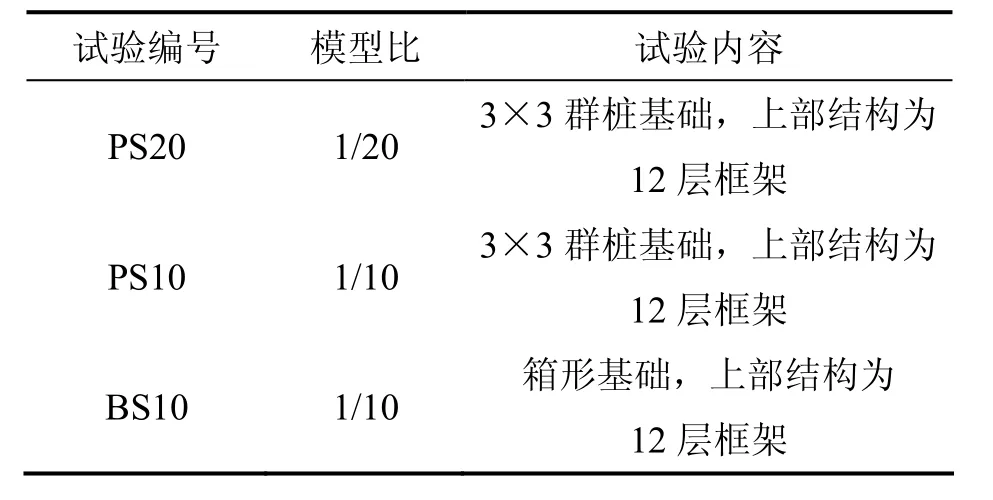
表2 非均匀分层中土-结构动力相互作用试验条件Table 2 Test conditions of SSDI system in nonuniform layers
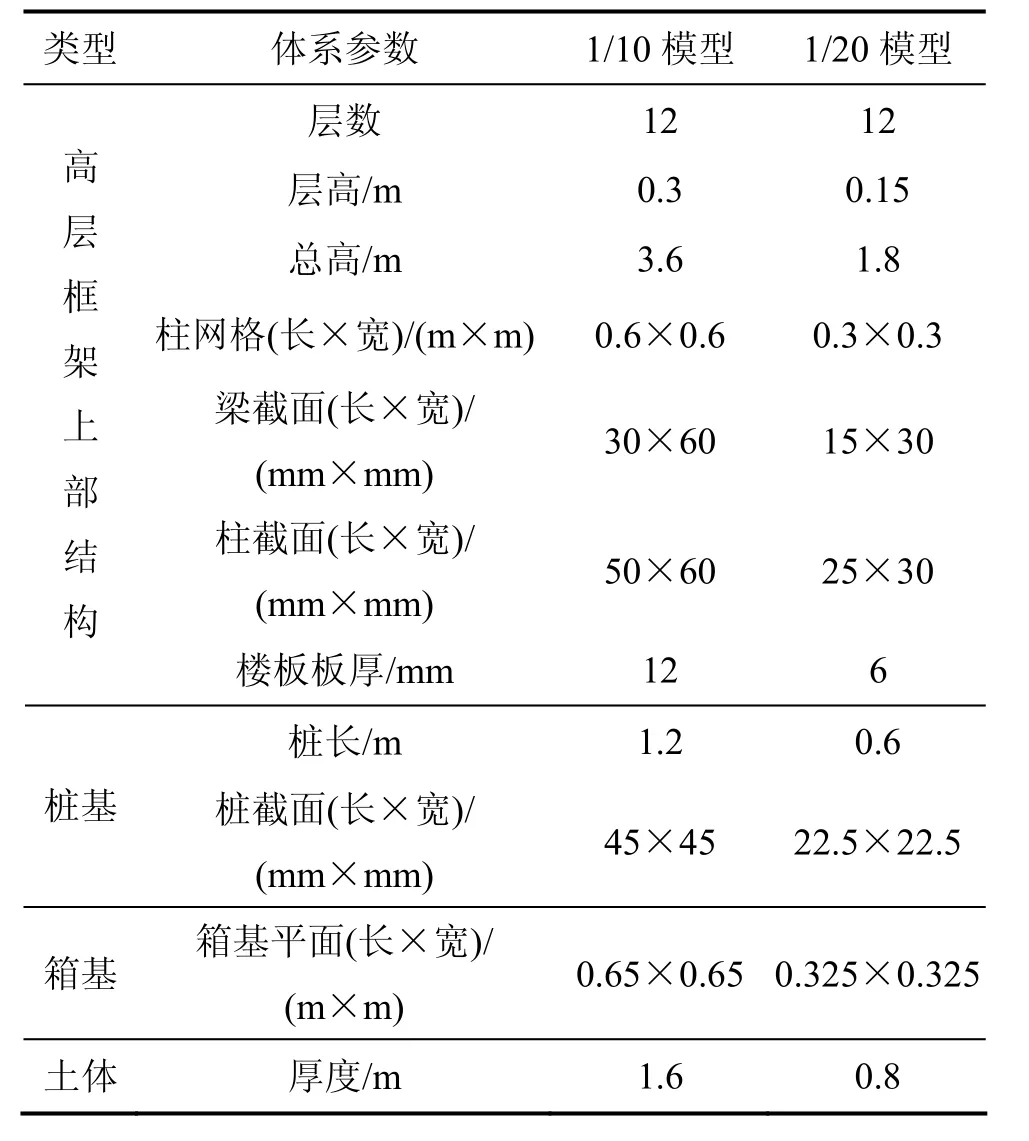
表3 土-结构动力相互作用体系模型概况Table 3 Model conditions of SSDI system
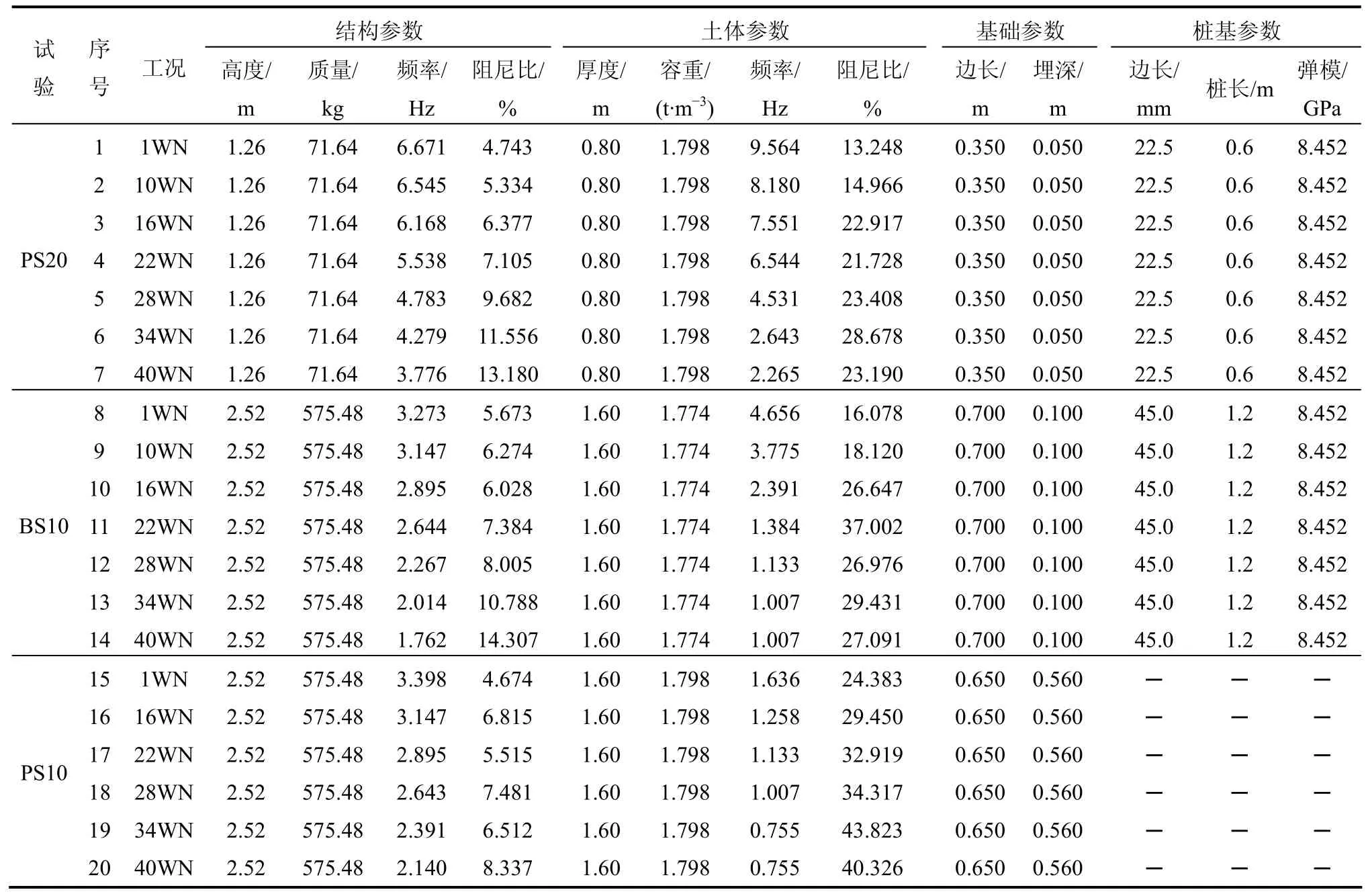
表4 非均匀分层土地基条件下土-结构动力相互作用体系各计算参数Table 4 Parameter of SSDI system on basement with heteropic and layered soil
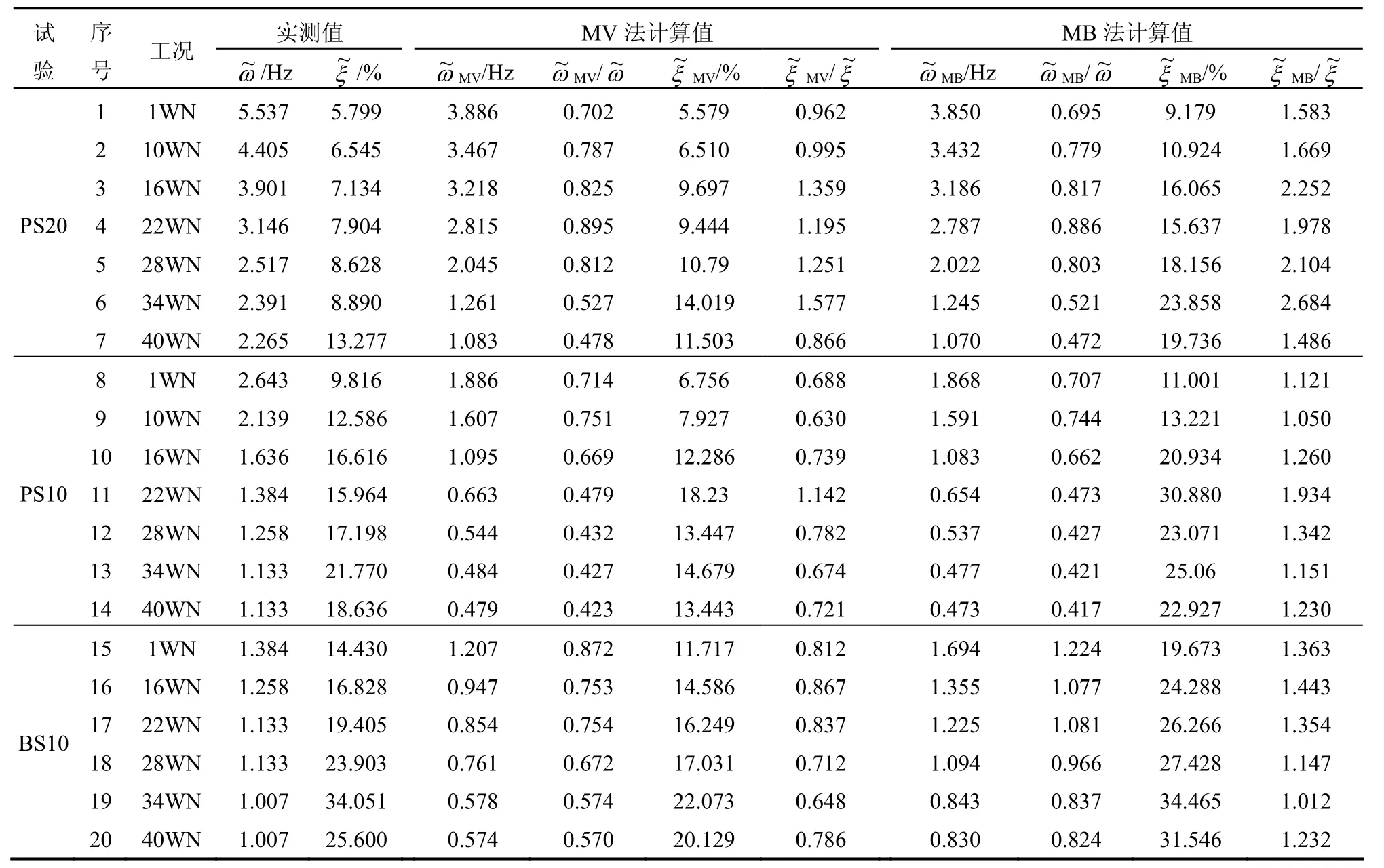
表5 MV法和MB法对非均匀分层土地基条件下土-结构动力相互作用体系频率及阻尼比计算结果对比Table 5 Contrast of frequency and damping ratio for SSDI system on basement with heteropic and layered soil using MV and MB methods
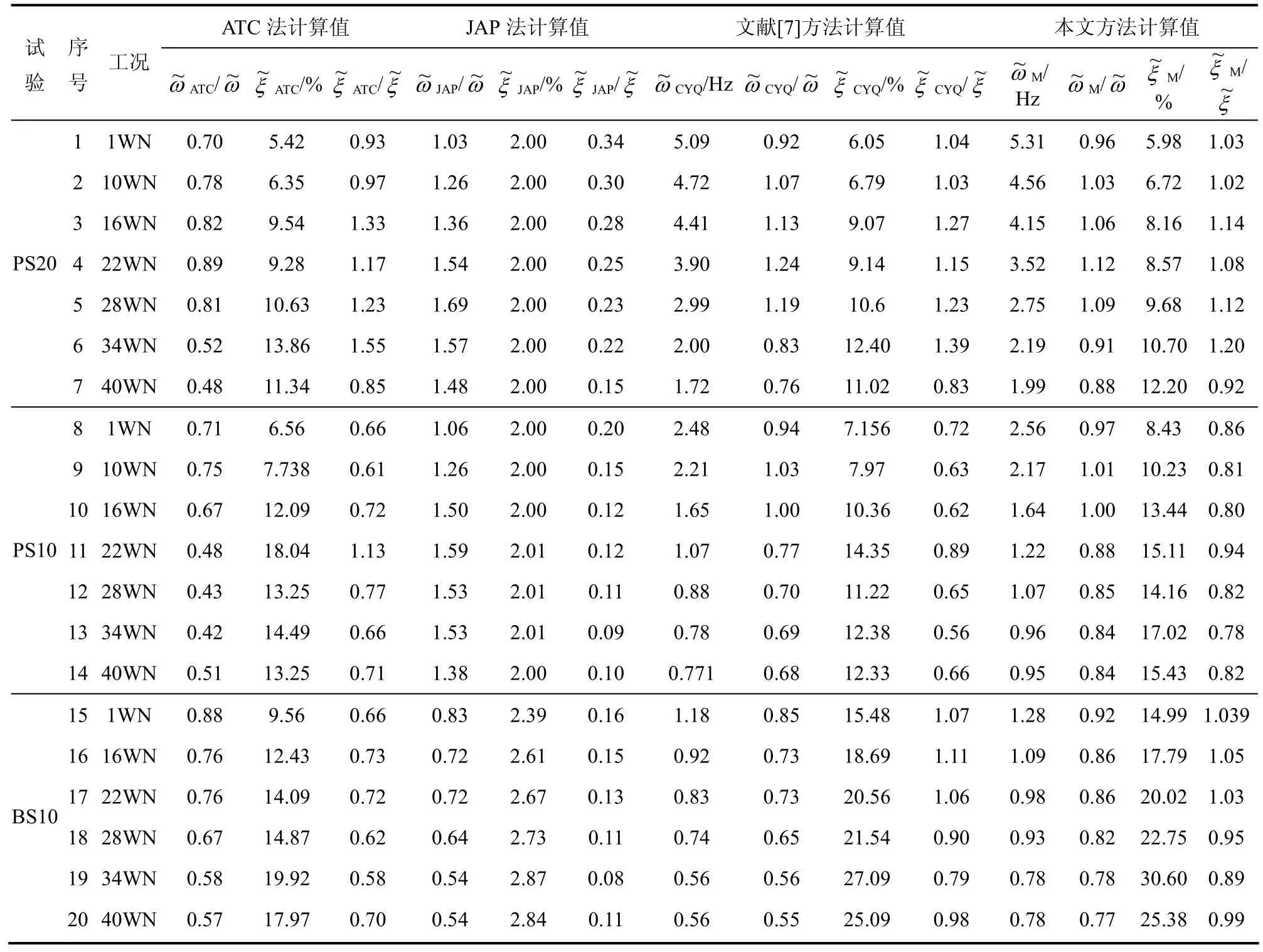
表6 ATC法和JAP法对非均匀分层土地基条件下土-结构动力相互作用体系频率及阻尼比计算结果对比Table 6 Contrast of frequency and damping ratio for SSDI system on basement with heteropic and layered soil using ATC and JAP methods
4 结论
(1) 提出的 SSDI体系非线性耦合阻尼比公式考虑上部结构的阻尼特性、地基土在基础平动与转动时辐射阻尼以及地基土的黏滞材料阻尼,据此可考量土-结构动力相互作用体系各部分的阻尼特性对整个体系阻尼的贡献程度。
(2) 使用所提出的非线性耦合阻尼比计算公式对算例进行计算,其计算结果与其他简化计算法所得结果相比相比更接近于实测结果,且误差控制在10%~20%,大幅度提高了计算精度。其误差的产生与结构及土体材料阻尼比的计算有关,同时也与试验实测数据本身的误差有关。
[1]王松涛, 曹资. 现代抗震设计方法[M]. 北京: 中国建筑工业出版社, 1997: 1-5.WANG Song-tao, CAO Zi. Modern seismic design method[M].Beijing: China Architecture & Building Press, 1997: 1-5.
[2]GB 50011—2001, 建筑抗震设计规范[S].GB 50011—2001, Code for seismic design of buildings[S].
[3]Veletsos A S, Verbic B. Vibration of viscoelastic foundations[J].Earthquake Engineering and Structural Dynamics, 1973, 2(1):87-102.
[4]Bielak J. Dynamic behavior of structures with embedded foundations[J]. International Journal of Earthquake Engineering and Structural Dynamics, 1975, 3(2): 259-274.
[5]美国建筑物抗震设计暂行条例(1978)[M]. 九国抗震设计规范汇编[M]. 北京: 地震出版社, 1982: 62-69.The United States of America Interim Regulations on the Seismic Design of Buildings(1978). Nine countries seismic design code compilation[M]. Beijing: Seismological Press, 1982:62-69.
[6]加藤大介他. 地震荷重ー地震动の予测と建筑物の応答[M].东京: 日本建筑学会, 1992: 25-28.Daisuke K. The earthquake ground motion to load for answering buildings[M]. Tokyo: Architectural Institute of Japan, 1992:25-28.
[7]陈跃庆, 吕西林, 李培振, 等. 结构-地基相互作用体系动力特性参数的简化计算方法[J]. 地震工程与工程振动, 2003,23(1): 71-77.CHEN Yue-qing, LÜ Xi-lin, LI Pei-zhen, et al. Simplified method for calculating dynamic characteristics of soil-structure interaction system[J]. Earthquake Engineering and Engineering Vibration, 2003, 23(1): 71-77.
[8]夏栋舟, 何益斌, 刘建华. 土-结构动力相互作用体系阻尼及地震反应分析[J]. 岩土力学, 2009, 30(10): 2923-2928.XIA Dong-zhou, HE Yi-bin, LIU Jian-hua. Study of damping property and seismic action effect for soil-structure dynamic interaction system[J]. Rock and Soil Mechanics, 2009, 30(10):2923-2928.
[9]樊海涛. 钢筋混凝土建筑非线性阻尼性能及其地震反应研究[D]. 长沙: 湖南大学土木工程学院, 2005: 38-54.FAN Hai-tao. The research on non-linear damping properties and seismic response of reinforced concrete buildings[D]. Changsha:Hunan University. College of Civil Engineering, 2005: 38-54.
[10]Hardin M J. Mats and combined footings analysis by the finite element methods[J]. Proc ACI, 1971, 68: 945-949.
[11]袁晓铭, 孙锐, 孙静, 等. 常规土类动剪切模量比和阻尼比试验研究[J]. 地震工程与工程振动, 2000, 20(4): 133-139.YUAN Xiao-ming, SUN Rui, SUN Jing, et al. Laboratory experimental study on dynamic shear modulus ratio and damping ratio of soils[J]. Earthquake Engineering and Engineering Vibration, 2000, 20(4): 133-139.
[12]Apsel R J, Luco J E. Impedance functions for foundations embedded in a layered medium: An integral equation approach[J]. International Journal of Earthquake Engineering and Structural Dynamics, 1987, 15(2): 213-231.

