考虑卸荷及变形影响的基坑挡墙土压力
欧明喜,刘新荣 ,石建勋
(1. 重庆大学 土木工程学院,重庆,400045;2. 重庆大学 山地城镇建设与新技术教育部重点实验室,重庆,400045)
随着城市建设的发展,高层建筑地下室的建设和城市地铁工程的建设,深基坑工程将越来越多[1]。由于这些工程大多分布在城市中心地带,周围环境对工程设计和施工提出了更高的要求。现行深基坑支护结构设计采用的弹性支点法在计算墙后主动土压力时采用经典的朗肯土压力理论,墙前被动区也只考虑了挡墙变形的线性影响。国内外许多学者对土压力进行了研究。Terzaghi[2]通过大规模的模型试验获得了极限状态和挡土结构位移的关系,并认为只有当土体水平位移达到一定值、土体产生剪切破坏时,Coulomb和Rankine土压力才是正确的。Fang等[3-4]对砂性填土刚性挡墙的主动和被动土压力进行了模型试验研究,对土压力及分布规律进行了探索。杨斌等[5]通过一定数量的室内模型试验研究,得出了挡土结构位移和侧土压力强度之间的关系,提出了一种考虑挡土结构侧向位移的侧土压力简化计算方法。陈页开等[6-7]采用有线单元法对作用在刚性挡土墙上的主动、被动土压力进行数值分析,研究了不同挡土墙的变位模式、不同墙面摩擦特性以及土体变形特性等因素对土压力及其分布的影响。卢坤林等[8-9]分析了位移对主动、被动土压力的影响规律,用双曲线函数拟合松弛应力、挤压应力与位移的关系,推导了考虑位移影响的朗肯土压力理论。邓子胜等[10]根据横向受荷桩的p-y曲线建立了可考虑挡土墙位移非线性影响的土压力计算模型。梅国雄等[11]根据土压力随挡土墙位移的变化特点提出了考虑变形的土压力方法。这些研究有的是在分析土压力与挡墙位移关系的基础上采用某种数学函数进行拟合,这不能从机理上解释挡墙位移对土压力的影响;有的是通过模型试验进行土压力研究,但是,试验中普遍存在的问题就是忽略了基坑开挖过程中土体的应力路径与常规的试验不同。针对这些问题,本文作者采用不同卸荷应力路径试验得到的土体应力应变关系,建立考虑卸荷及变形影响的非极限主动、被动土压力计算公式,将基坑挡墙变形与土压力关系发展的宏观现象从微观上的土体应力应变关系进行解释。
1 基坑开挖土体应力路径
在深基坑开挖过程当中,挡墙变形会对挡墙前后一定区域内的土体产生扰动。受到扰动影响区域的土体有2种常见的应力路径模式,如图1中的A和B2点所示。A点随着基坑的开挖表现为竖向压力不变,横向压力减小;B点随着基坑的开挖表现为竖向压力减小,横向压力增加。这分别对应于室内不同应力路径的卸荷试验,前者对应于轴压不变围压减小,后者则对应于轴压较小围压增大。
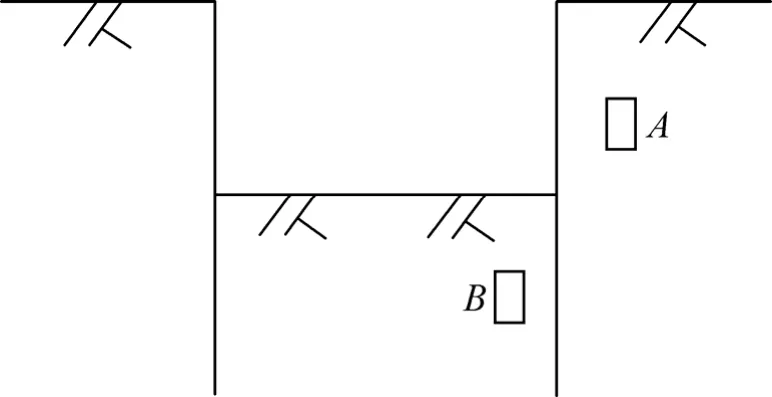
图1 不同应力路径代表点Fig.1 Representative points of different stress paths
2 基坑土体应变状态模式
Caspe[12]通过对深基坑挡土墙后主动区土体的变形状态的分析,提出了一种墙后土体应变状态模式的假设,将墙后土体分为塑性平衡区、弹性平衡区及未受扰动区,各分区的分界线为对数螺旋线。并假设塑性平衡区各点的水平应变相等,弹性平衡区水平应变随距离挡墙距离的增大而呈线性减小,但是,这种假设没能满足挡墙与土体的位移协调条件。李蓓等[13]对其进行了改进,使其满足位移协调的条件,但仍然将墙后扰动区分为塑性区与弹性区且塑性区各点水平应变相等。而实际上,随着距墙体的距离增加,水平应力减小,水平各点的应变应该逐渐减小,且扰动区不会存在明显的弹性、塑性区分界面。
基于以上考虑,本文将挡土墙前、后土体分为扰动区与非扰动区,分界面为朗肯被动破裂面与朗肯主动破裂面,如图2所示。图2中:z为计算点深度;δ(z)为深度z处的挡墙位移(主动侧变形为正,被动侧变形为负);L为深度z处挡墙到滑裂面的距离;H为地面到挡墙变形为零处深度;h为当前开挖深度;d为开挖面到变形为零处深度。杨斌等[5]认为滑裂面以外土体的水平位移很小,在挡板侧向平移过程中,土体的侧向变形主要分布在滑裂面以内,所以,可以认为墙体的变形主要是扰动区土体的水平应变所致。于是,可以假定扰动区各点水平应变为
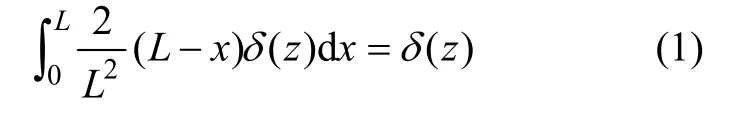
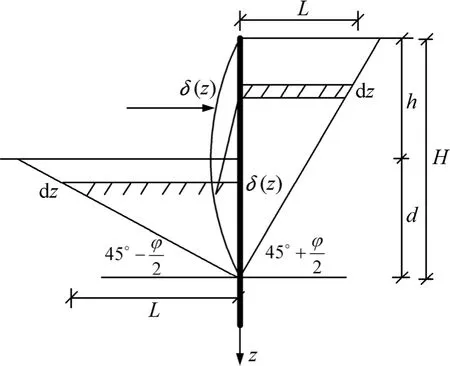
图2 挡土墙前后土体应变状态模式Fig.2 Stain state mode for soil in both sides of retaining wall
其中:x为计算点到挡土墙的距离。这样,深度z处土体的变形等于该处墙体位移,满足位移协调条件。
3 土体卸荷应力-应变关系
在基坑开挖过程中,挡土墙前后的土体表现为卸荷应力路径。与常规进行的三轴试验不同,刘国彬等[14]对上海地区3种典型的软土进行了一系列的应力路径试验,对软土的卸荷应力应变关系进行了较深入的研究。试验表明:对于同一种卸荷,应力路径在不同固结压力作用下的土体的应力应变关系曲线基本相似,为双曲线型。并且在同样的卸荷应力路径条件下应力应变关系可以用平均固结压力进行归一化,归一化的方程为:
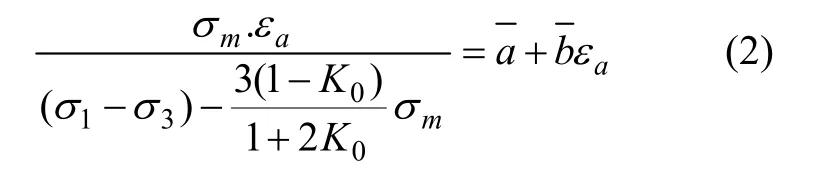
式中:εa为轴向应变;分别为归一化直线在纵坐标上的截距与斜率;σ1为轴向压力(kPa);σ3为围压(kPa);K0为静止土压力系数;为平均固结压力(kPa);σ1c为固结轴压(kPa);σ3c为固结围压(kPa)。
4 考虑卸荷及变形的土压力公式推导
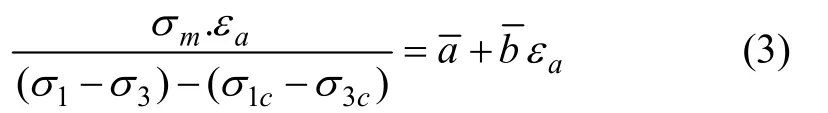
将以上各项代入式(3),可以得到非极限土压力计算公式:
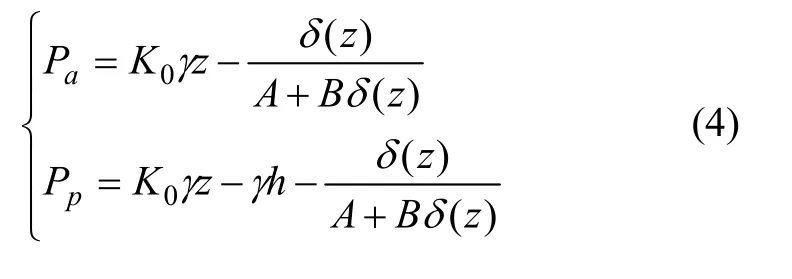
式中:
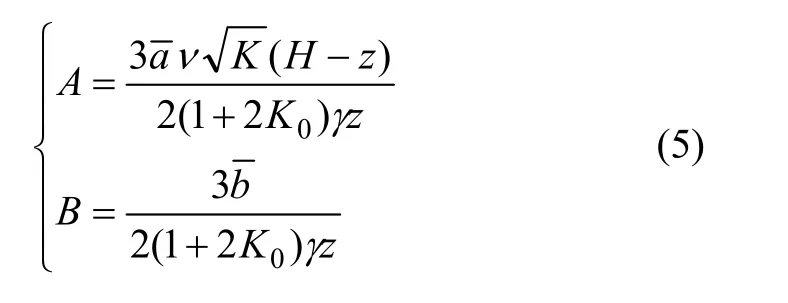
在计算中,须特别注意的是:δ(z)在计算非极限主动土压力时取正值,计算非极限被动土压力时取负值;在计算非极限主动土压力时,应分别采取轴向压力不变、围压减小的应力路径情况下归一化曲线的纵坐标截距和斜率,在计算非极限被动土压力时,应分别采用轴压减小、围压增大应力路径情况下归一化曲线的纵坐标与斜率;H为地面到挡土墙位移零点的距离,文献[13]认为可以取为(2.0~2.2)h,h为当前工况下已开挖深度;在计算非极限主动土压力时,取计算非极限被动土压力时,取
5 算例分析
为了说明本文所推导的考虑卸荷及变形影响的土压力计算公式的实用性和合理性,下面用1个简单算列进行分析。
5.1 计算参数
假设基坑开挖深度为10 m,土体为文献[14]中的淤泥质黏土均质土层,取H=2.2h=22 m,基本参数如下:重度为γ=16.5 kN/m3;内摩擦角φ=8.0°,φ'=12.0°;静止土压力系数泊松比为
5.2 土压力与挡墙变形的关系
经计算,不同深度处非极限主动土压力随挡墙变形的关系如图3所示。由图3可知:非极限主动土压力随挡墙变形的增大而单调减小,曲线斜率逐步减小最后趋于平缓,说明在挡墙刚开始变形时很小的变形增量能够产生很大的土压力降低,且埋深越深,这种变化趋势越明显。
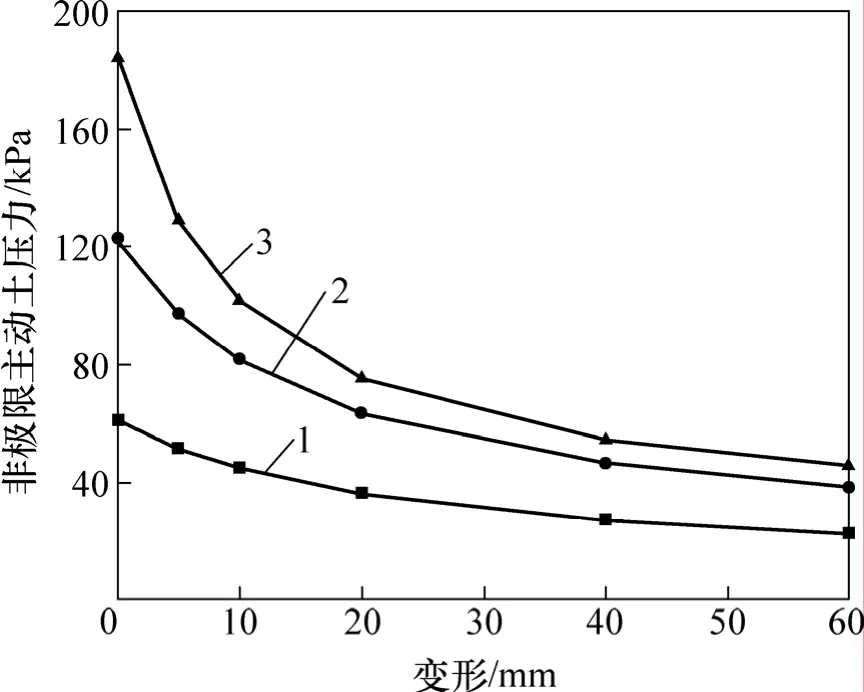
图3 非极限主动土压力与挡墙变形的关系Fig.3 Relation between non-limit state active earth pressure and deformation of retaining wall
不同深度处非极限被动土压力随挡墙变形的关系如图4所示。由图4可知:非极限被动土压力随挡墙变形的增大而单调增大,曲线斜率逐步减小最后趋于平缓,说明在挡墙刚开始变形时很小的变形增量能够产生很大的土压力增大,且埋深越深,这种趋势表现得愈明显。
图5所示为基坑开挖完成后z=15 m处挡墙前、后非极限土压力随挡墙变形的发展规律(图5中横坐标负号仅表示变形的方向,不表征位移大小)。从图5可以看出:土压力的发展规律符合文献[8]中总结的土压力随位移的发展规律;非极限主动土压力随变形增大单调递减最后趋于平缓,非极限被动土压力随变形增大单调递增最后趋于平缓,这反映了计算公式的单调性与有界性的特点。
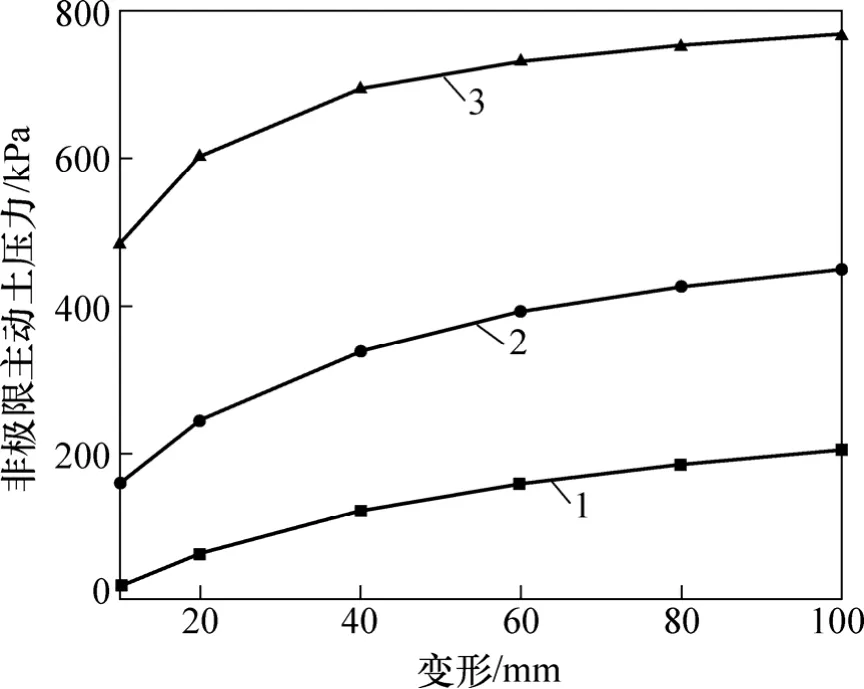
图4 非极限被动土压力与挡墙变形的关系Fig.4 Relation between non-limit state passive earth pressure and deformation of retaining wall
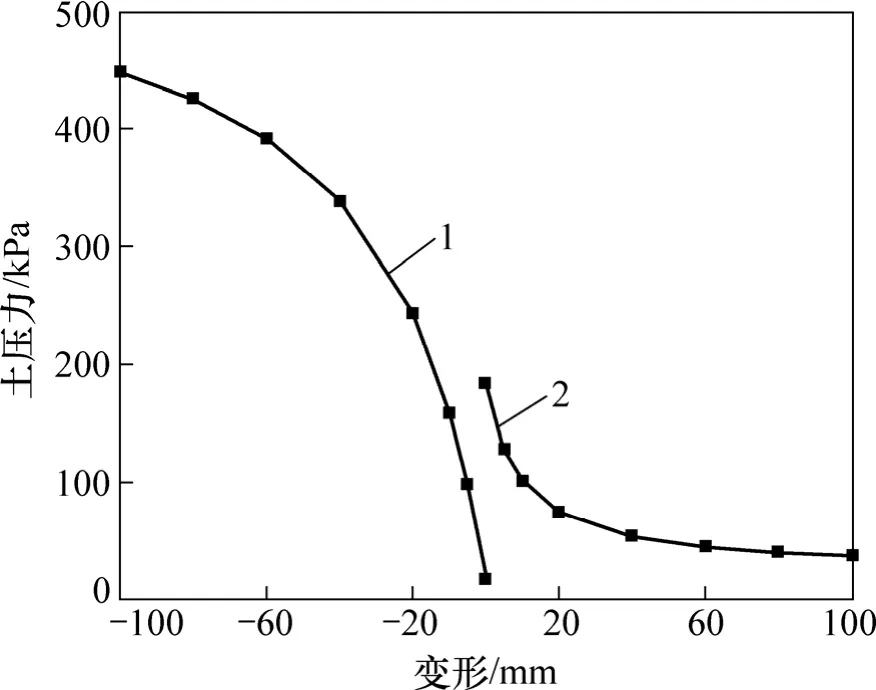
图5 水平土压力随挡墙变形的关系Fig.5 Relation between lateral earth pressure and deformation of retaining wall
5.3 土压力随深度的分布
王建华等[15]根据上海地区 50个深基坑工程的实测结果,研究了连续墙的变形特性。研究结果表明:绝大部分基坑的最大侧移位置在开挖面附近。基于本文对基坑挡墙的变形得出如图6所示的基坑挡墙变形。
假设基坑开挖到设计深度后,基坑挡墙在基底土体表面处的变形为 100 mm,经计算该工况下基坑挡土墙两侧土压力与分布如图7所示。从图7可以看出:计算的土压力沿深度分布规律与现行基坑支护设计采用的弹性支点法的计算结果极为接近,而且本文推导的计算公式能够反映挡墙对土压力的非线性影响。这说明本文推导的考虑卸荷及变形影响的土压力计算公式具有可行性和合理性。
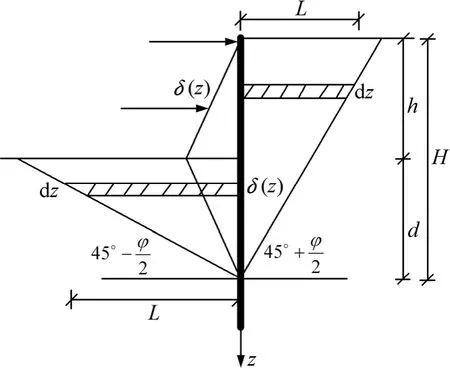
图6 基坑挡墙变形假定Fig.6 Deformation assumption for retaining wall of deep foundation pit
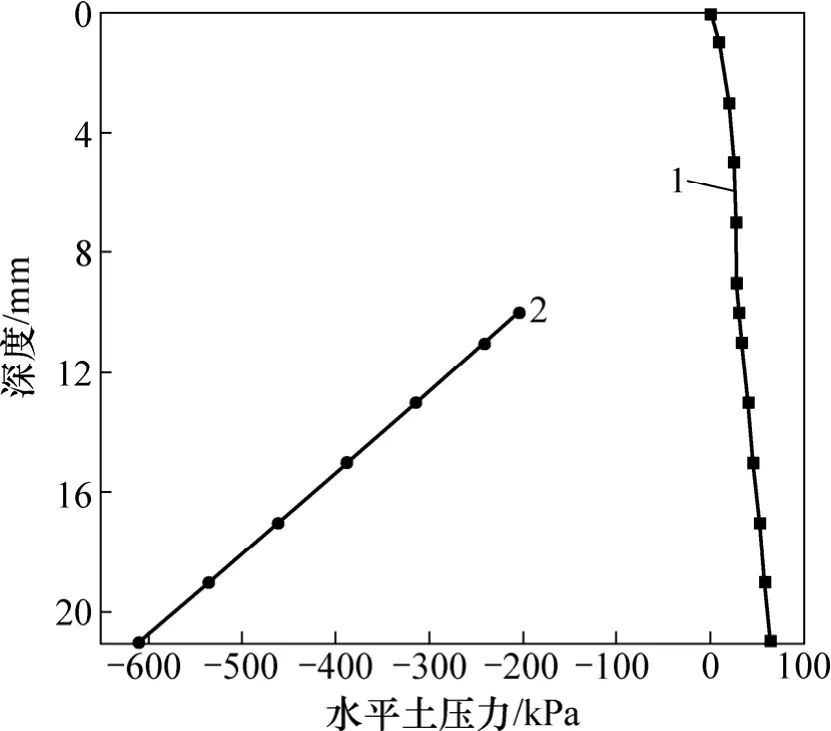
图7 水平土压力随深度的分布Fig.7 Lateral earth pressure distribution along depth
6 结论
(1) 基于深基坑挡土墙两侧土体的应变模式假设,采用考虑卸荷应力路径的土体应力应变关系,在假定土体侧向应变与轴向应变呈线性关系的基础上建立了能够考虑位移非线性影响的非极限主动、被动土压力计算公式。
[1]杨光华. 深基坑支护结构的实用计算方法及其应用[M]. 北京:地质出版社, 2004: 1-16.YANG Guang-hua. Practical calculation methods and application for retaining structure of deep foundation pit[M]. Beijing:Geology Press, 2004: 1-16.
[2]Terzaghi K. Record earth pressure testing machine[J].Engineering News Record, 1932,109(29): 365-369.
[3]Fang Y S, Ishibashi I. Static earth pressures with various wall movements[J]. Journal of Geotechnical Engineering, ASCE,1986,112(3): 317-333.
[4]Fang Y S, Chen T J, Wu B F. Passive earth pressure with various wall movements[J]. Journal of Geotechnical Engineering, ASCE,1994, 120(8): 1307-1323.
[5]杨斌, 胡立强. 挡土结构侧土压力与水平位移关系的试验研究[J]. 建筑科学, 2000, 16(2): 14-20.YANG Bin, HU Li-qiang. Test study on relationship between lateral earth pressure acting on retaining structures and horizontal displacement[J]. Building Science, 2000, 16(2):14-20.
[6]陈页开, 汪益敏, 徐日庆, 等. 刚性挡土墙被动土压力数值分析[J]. 岩石力学与工程学报, 2004, 23(6): 980-988.CHEN Ye-kai, WANG Yi-min, XU Ri-qing, et al. Numerical analyses of passive earth pressure on rigid retaining wall[J].Chinese Journal of Rock Mechanics and Engineering,2004, 23(6): 980-988.
[7]陈页开, 汪益敏, 徐日庆, 等. 刚性挡土墙主动土压力数值分析[J]. 岩石力学与工程学报, 2004, 23(6): 989-995.CHEN Ye-kai, WANG Yi-min, XU Ri-qing, et al. Numerical analyses of active earth pressure on rigid retaining wall[J].Chinese Journal of Rock Mechanics and Engineering, 2004,23(6): 989-995.
[8]卢坤林, 杨扬. 非极限被动土压力的近似计算方法[J].合肥工业大学学报: 自然科学版, 2009, 32(4): 523-527.LU Kun-lin, YANG Yang. Calculation of unlimited passive earth pressure[J]. Journal of Hefei University of Technology,2009, 32(4): 523-527.
[9]卢坤林, 杨扬. 考虑位移影响的主动土压力近似计算方法[J].岩土力学, 2009, 30(2): 553-557.LU Kun-lin, YANG Yang. Approximate calculation method ofactive earth pressure considering displacement[J]. Rock and Soil Mechanics, 2009,30(2): 553-557.
[10]邓子胜, 邹银生, 王贻荪. 考虑位移非线性影响的挡土墙土压力计算模型研究[J]. 中国公路学报, 2004, 17(2): 24-27.DENG Zi-sheng, ZOU Yin-sheng, WANG Yi-sun. Study of calculation model of the earth pressure for retaining wall considering the nonlinear influence of the displacement[J]. China Journal of Highway and Transport, 2004, 17(2): 24-27.
[11]梅国雄, 宰金珉. 考虑位移影响的土压力近似计算方法[J].岩土力学, 2001, 22(4): 83-85.MEI Guo-xiong, ZAI Jin-min. Earth pressure calculating method considering displacement[J]. Rock and Soil Mechanics, 2001,22(4): 83-85.
[12]Caspe M S. Surface settlement adjacent to braced open cuts[J].Journal of Soil Mechanics and Foundation Engineering,American Society of Civil Engineering, 1966, 92(SM4): 51-59.
[13]李蓓, 赵锡宏. 一种考虑挡土墙变形的深基坑非线性土压力方法[J]. 岩土力学, 2004, 25(增2): 453-458.LI Bei, ZHAO Xi-hong. A nonlinear earth pressure method for deep excavation considering deformation of retaining wall[J].Rock and Soil Mechanics, 2004, 25(Suppl.2): 453-458.
[14]刘国彬, 侯学渊. 软土的卸荷应力应变特性[J]. 地下工程与隧道, 1997(2): 16-23.LIU Guo-bin, HOU Xue-yuan. Unloading stress-strain characteristic for soft soil[J]. Underground Engineering and Tunnel, 1997(2): 16-23.
[15]王建华, 徐中华, 陈锦剑, 等. 上海软土地区深基坑连续墙的变形特性浅析[J]. 地下空间与工程学报, 2005, 1(4): 485-489.WANG Jian-hua, XU Zhong-hua, CHEN Jin-jian, et al,Deformation properties of diaphragm wall due to deep excavation in Shanghai soft soil[J]. Chinese Journal of Underground Space and Engineering, 2005, 1(4): 485-489.

