矩形渡槽流固耦合体系风致的动力性能

刘亮，张华，郜余伟

(河海大学 土木与交通学院，江苏 南京，210098)

渡槽作为一种重要的输水建筑，在我国各地有较广泛的应用。自20世纪80年代以来，我国渡槽风毁事故发生得比较多[1-2]，由此产生巨大的经济损失。目前，关于渡槽抗风问题的研究较多的是将风力看作静风荷载，而对渡槽风振的研究不足。风的脉动效应不仅影响渡槽结构的疲劳寿命，而且在某些情况下会引起共振，增加了结构破坏的危险性，因此，对渡槽风振响应进行研究对其抗风设计具有现实的工程意义。风致振动引起的水体晃动对渡槽结构的风振响应产生一定的影响，在渡槽结构的风振分析时，水体和槽壁之间的流固耦合作用不容忽视[3-5]；此外，对不同高宽比的渡槽，其结构的风振动力性能和稳定性可能有较大的差异。在此，本文作者通过自回归滑动平均(ARMA)模型模拟脉动风，假设水体是无黏性、不可压缩、无旋的，并采用任意拉格朗日-欧拉(ALE)方法求解流固耦合问题，对比分析不同高宽比的矩形渡槽流固耦合体系在多种工况下的风振动力性能。

1 流固耦合系统基本方程

1.1 流体控制方程

为解决流固耦合面的协调问题，任意拉格朗日-欧拉(ALE)方法允许网格在计算空间以任意形式运动，在进行流固耦合计算时，令网格运动方式与流体晃动方式相同，以维持计算网格的合理形状并准确描述流体的晃动界面，从而将对水体运动的计算简化为弹性力学的几何非线性动力计算。基于 ALE描述的Navier-Stokes流体控制方程可表示为[6-8]：

式中：u为位移；u˙和u˙˙分别为u随时间的一阶和二阶微分；P为水压力；f为体力；ρ为流体密度；τ为黏性应力。

1.2 基于ALE描述的流固耦合边界条件

在风荷载作用下，槽体和流体之间的动力相互作用通过耦合面传递。在流固耦合体系中，渡槽结构的振动引起流体的晃动，在耦合面上，晃动的流体以压力的形式反作用于渡槽结构，影响结构的变形和应力分布。因此，流固耦合界面上槽体和流体须满足位移连续性和相互作用力平衡条件。

位移连续性：

作用力平衡：

式中：uf和us分别为耦合界面上流体和槽体结构的位移；σf和σs分别为耦合界面上流体和槽体结构的应力；nf和ns分别为流体和槽体结构耦合界面上的法向向量。在自由液面上，流体的法向速度等于液面的法向速度[9]：

式中：ξ为自由液面上节点的坐标；t为时间；v(ξ,t)为自由液面流体的速度；x˙(ξ,t)为自由液面的速度；n为自由液面单位法向量；Ωfree为自由液面。

1.3 结构风振方程

渡槽作为水工结构工作时不允许开裂，在计算分析时不考虑结构材料的非线性。对于渡槽耦合体系的风振计算，需要将流固耦合面上的相互作用项附加到动力方程中，采用有限元方法求解的渡槽流固耦合系统风振方程可表示为[10-11]：

式中：M，C和K分别为结构的质量、阻尼和刚度矩阵；u，u˙和u˙˙分别为相对地面的水平位移、速度和加速度列向量；PW(t)为作用在结构上的脉动风荷载向量；PL(t)为槽内流体作用在槽身的水平力。

2 脉动风模拟

2.1 ARMA模型

ARMA 模型可以模拟具有时间相关性和空间相关性的随机风速时程。一般的线性过程常可用差分方程表示为[12-14]：

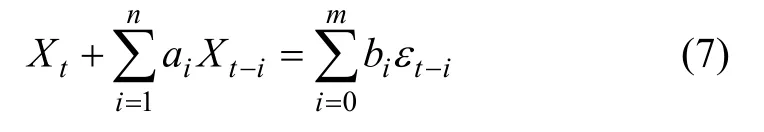
式中：Xt为平稳随机时间序列在时刻t的1个样本；Xt-i为平稳随机时间序列在时刻t-i的 1个样本；εt-i为白噪声；ai为自回归系数；bi为滑动平均系数；n为自回归阶数；m为滑动平均阶数。{Xt}称为n阶自回归m阶滑动平均过程，记为ARMA(n, m)。

将ARMA模型应用于m个脉动风速时程模拟，则

式中：U(t)为t时刻m阶脉动风速时程列阵；U(t-iΔt)为t-iΔt时刻m阶脉动风速时程列阵；X(t-jΔt) 为t-jΔt时刻m阶正态分布的白噪声列阵；p为自回归(AR)阶数；q为滑动回归(MA)阶数；Aj为m×m阶自回归(AR)系数矩阵；Bj为m×m阶滑动回归(MA)系数矩阵。

取b0≡1，得到工程上常用的表达式：

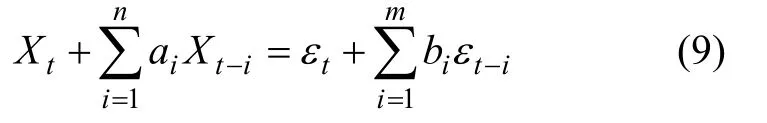
引入时移算子B:BiXi=Xi-1，可将式(8)写为：

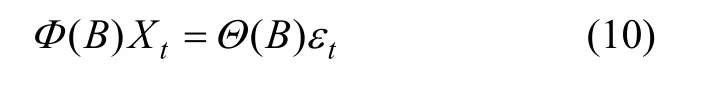
其中：

ARMA模型的平稳与可逆条件分别由自回归系数和滑动平均系数决定，可由Φ(B)=0和Θ(B)=0的根是否全部在B平面单位圆之外来判断。

2.2 渡槽结构脉动风荷载模拟

选用排架式矩形渡槽作为研究对象，渡槽支撑排架高24.0 m，槽壁厚0.5 m，单跨长10 m，如图1所示。槽身采用C50混凝土，密度为2.5 t/m3，弹性模量E=3.45×104MPa，泊松比μ=0.167；支撑排架采用C30混凝土，密度为2.5 t/m3，弹性模量E=3.00×104MPa，泊松比μ=0.167。当地基本风压为350 Pa/m2，地貌类别为B类。应用ARMA模型，在MATLAB平台上编制了脉动风的模拟程序，目标功率谱采用Davenport谱，时间步长Δt=0.1 s，时程总长T=120 s。通过程序模拟得到7条迎风面不同高度的脉动风速样本时程曲线。这里仅给出作用在支撑排架顶端处(距地面高度24 m)的脉动风速样本时程曲线，如图2所示。图3所示为渡槽结构模拟出的风速功率谱与目标谱对比结果。从图3可以看出：两者的曲线拟合程度较好，证明ARMA模型可以对脉动风进行有效模拟。将模拟得到的脉动风速时程与相应高度位置的平均风速叠加，依据相关规范[15]得到作用在渡槽迎风面上不同高度位置的风荷载强度样本时程。图4所示为作用在排架顶端处的风荷载强度样本时程曲线。

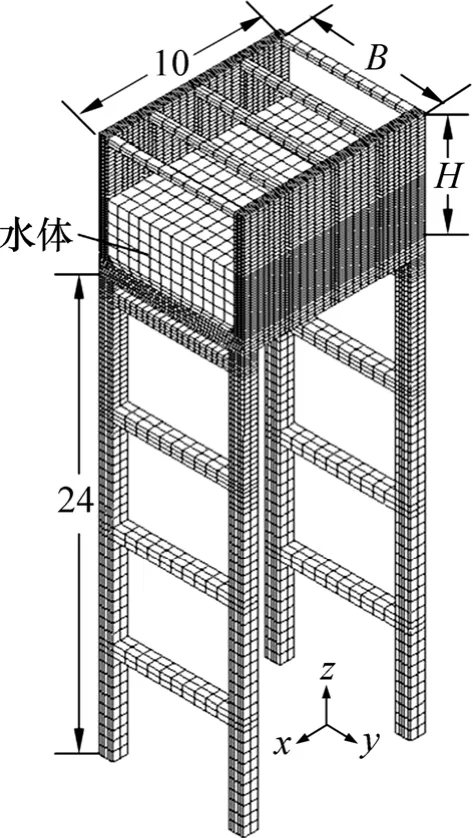
图1 渡槽三维有限元模型Fig.1 Diagram of three-dimensional model of aqueduct

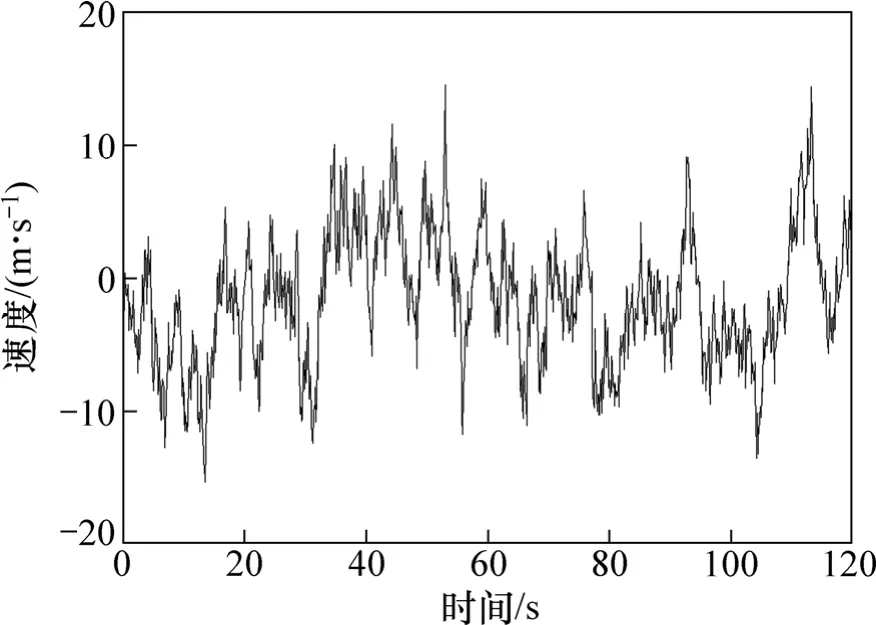
图2 支撑排架顶端处的脉动风速样本时程曲线Fig.2 Relationship between fluctuating wind velocity and time on top of framed bent

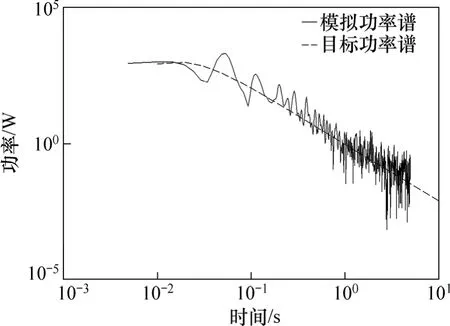
图3 排架顶端处的模拟功率谱与目标功率谱比较Fig.3 Comparison of power spectrum between simulation results and target results

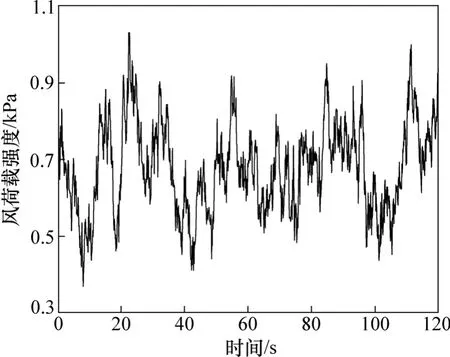
图4 排架顶端处的风荷载强度样本时程曲线Fig.4 Relationship between fluctuating wind load and time on top of framed bent

3 风振响应分析

运用有限元软件ADINA建立三维渡槽计算模型，渡槽结构采用三维实体单元模拟，槽内水体采用三维流体单元模拟，水体的体积模量为2.1 GPa。渡槽内壁与水体相互作用面采用流固耦合边界条件，水体上表面采用自由液面边界条件，进水和出水断面采用可滑移的壁面边界模拟。为考虑邻跨渡槽的影响，将邻跨渡槽(包括水体)的质量的一半附加在支撑排架的顶端。

为研究不同截面高宽比对渡槽风振性能和稳定性的影响，本文采用 4种截面高宽比的矩形渡槽：H/B=0.6(满槽水深H=4.8 m，槽身净宽B=8.1 m)，H/B=0.8(H=5.6 m，B=7.0 m)，H/B=1.0(H=6.2 m，B=6.2 m)和H/B=1.2(H=6.9 m，B=5.7 m)。此外，考虑到不同水深工况下，渡槽流固耦合体系的风振响应情况可能存在较大的差异，根据等流量的原则，对于不同高宽比的渡槽，分别选用6种水深工况进行渡槽风振的对比分析，水深工况参数见表1。

表1 不同高宽比矩形渡槽水深工况对比Table 1 Water depth conditions of different depth-width ratio aqueducts m

3.1 动位移分析

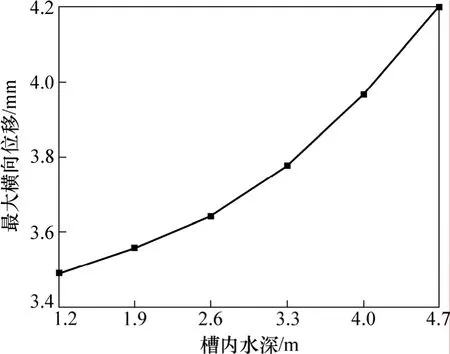
图5 高宽比为0.8的渡槽在不同水深下的跨中槽顶最大横向位移曲线Fig.5 Curves of maximum transversal displacement of structural top of aqueduct under different conditions

图5 所示为H/B=0.8的渡槽在6种水深下跨中槽顶最大横向位移曲线。从图5可以看出：对于同一截面高宽比的渡槽，随着水深的增大，槽内水位越高，渡槽槽顶的横向位移的增幅越大。为研究渡槽截面不同高宽比对渡槽结构横向位移的影响，作出高宽比分别为0.6，0.8，1.0和1.2的渡槽在同一流量工况下(工况6)跨中槽顶横向位移时程曲线，如图6所示。从图6可见：在等流量工况下，随着渡槽截面高宽比的增大，槽顶横向位移的增幅较大，表明渡槽截面的高宽比对渡槽结构横向振动的影响较显著。

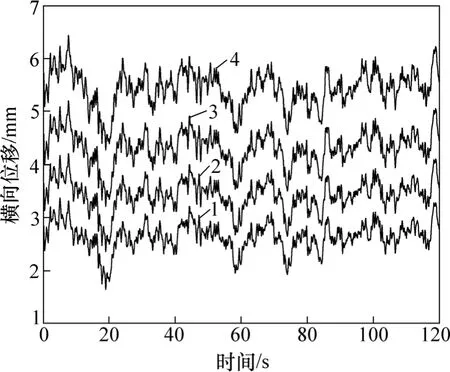
图6 不同高宽比的渡槽在同一流量下跨中槽顶横向位移时程曲线Fig.6 Curves of transversal displacement of structural top of different depth-width ratio aqueducts

3.2 倾覆力矩分析

图7所示为H/B=0.6的渡槽在水深4.103 m下跨中槽身右下角处的倾覆力矩时程曲线。受到水体晃动的影响，渡槽倾覆力矩变化较为剧烈。图8所示为截面高宽比为0.6，0.8，1.0和1.2的渡槽在6种水深(见表1)下跨中槽身右下角处的最大倾覆力矩曲线。从图7和图8可见：对于同一高宽比的渡槽，随着水深的增大，其倾覆力矩呈近似线性增大趋势。对比不同高宽比渡槽的倾覆力矩曲线可以看出：在同一流量工况下，随着高宽比的增大，渡槽倾覆力矩随之减小。

3.3 动水压力分析

图9所示为H/B=1.2的渡槽在水深 2.147 m和5.831 m下跨中槽壁右下角处的动水压力时程曲线。由图9可以看出：在低水位和高水位下，渡槽动水压力的风振时程响应规律基本一致。在这2种工况下，静水压力分别为21.041 kPa和57.144 kPa，而动水压力最大分别达到20.173 kPa和54.765 kPa，均约为其各自静水压力的95.8%。

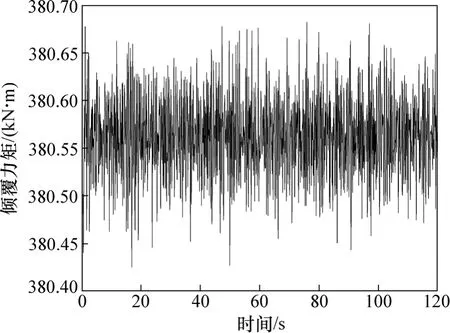
图7 高宽比为0.6的渡槽在4.103 m水深工况下跨中槽身右下角处的倾覆力矩时程曲线Fig.7 Curve of upsetting moment of aqueduct

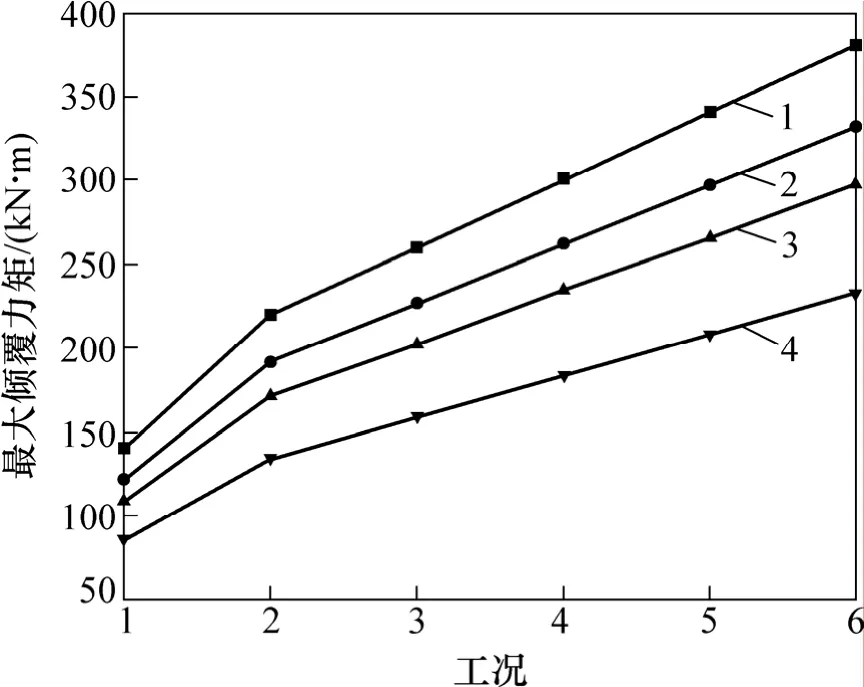
图8 不同高宽比渡槽在6种工况下跨中槽身右下角处的最大倾覆力矩曲线Fig.8 Curves of maximum upsetting moment of different depth-width ratio aqueducts

图10所示是H/B为0.6，0.8，1.0和1.2的渡槽在 6种水深工况(见表1)下跨中槽壁右下角处的最大动水压力曲线。相同高宽比的渡槽，其动水压力随着水深的变化呈近似线性变化。由表1和图10可以看出：在等流量工况下，H/B大的渡槽槽内水位较H/B小的渡槽槽内的水位高，且前者结构的风振位移响应也较大，因此，计算结果出现渡槽动水压力随着高宽比的增大而增大的现象。

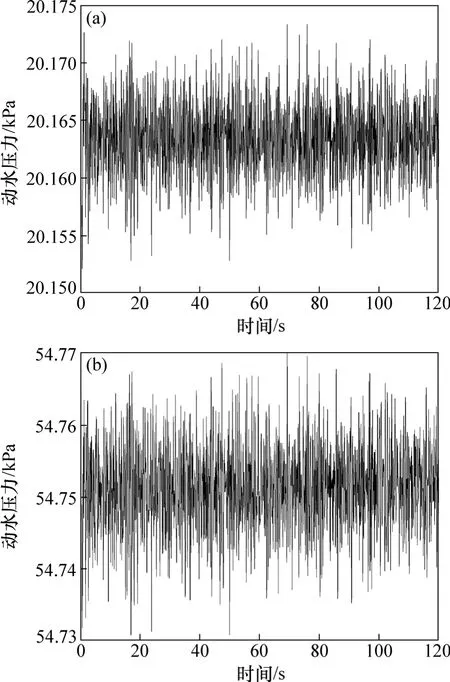
图9 高宽比为1.2的渡槽跨中槽壁右下角处动水压力时程曲线Fig.9 Curves of dynamic water pressure of central span with depth-width ratio of 1.2

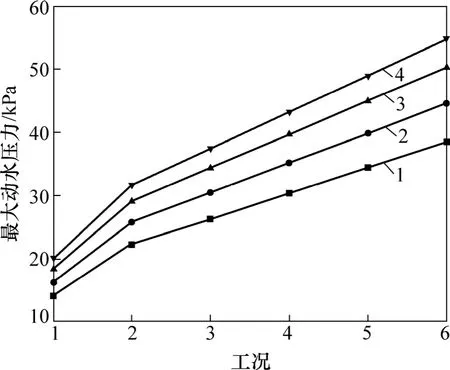
图10 不同高宽比矩形渡槽在6种工况下跨中槽壁右下角处的最大动水压力曲线Fig.10 Curves of maximum dynamic water pressure of different depth-width ratio aqueducts

4 结论

(1) 随着槽内水深的增大，不同高宽比的渡槽风振响应变化规律相似：渡槽横向位移、倾覆力矩及动水压力的风振响应均显著增强，且渡槽槽内水位越高，水体对渡槽位移风振响应的影响越大。

(2) 在风荷载作用下，水体的晃动使得倾覆力矩的变化非常剧烈。渡槽与水体相互作用产生的动水压力接近静水压力,在渡槽设计的内力计算时动水压力不容忽视。

(3) 在等流量水深工况下，随着渡槽截面高宽比增大，渡槽结构的横向位移和动水压力明显增大，但其倾覆力矩随之减小。因此，在渡槽抗风设计时，选择截面高宽比时，要综合考虑不同高宽比对结构振动和稳定性的影响。

[1]李遇春, 楼梦麟. 排架式渡槽流-固耦合动力特性分析[J]. 水利学报, 2000(12): 31-37.LI Yu-chun, LUO Meng-lin. Dynamic characteristics of fluid-structure interaction system for bent-type aqueduct[J].Journal of Hydraulic Engineering, 2000(12): 31-37.

[2]李正农, 楼梦麟, 宋锦忠, 等. U形渡槽槽体结构风载体形系数的风洞试验研究[J]. 空气动力学学报, 2002, 20(2): 233-238,245.LI Zheng-nong, LUO Meng-lin, SONG Jin-zhong, et al. The wind tunnel test study on wind load shape coefficient of body structure for U shape[J]. Acta Aerodynamica Sinica, 2002, 20(2):233-238, 245.

[3]吴轶, 莫海鸿, 杨春. 排架-渡槽-水三维耦合体系地震响应分析[J]. 水利学报, 2005, 36(3): 280-285.WU Yi, MO Hai-hong, YANG Chun. Seismic response of frame-supported large rectangular aqueduct-water 3-D coupling system[J]. Journal of Hydraulic Engineering, 2005, 36(3):280-285.

[4]徐建国, 陈淮, 王博, 等. 大型渡槽结构考虑耦合的动力建模研究[J]. 南京理工大学学报, 2005, 29(6): 639-644.XU Jian-guo, CHEN Huai, WANG Bo, et al. Dynamic modeling study of aqueduct structure coupling[J]. Journal of Nanjing University of Science and Technology, 2005, 29(6): 639-644.

[5]徐建国, 陈淮, 王博, 等. 考虑流固动力相互作用的大型渡槽地震响应研究[J]. 土木工程学报, 2005, 38(8): 67-73.XU Jian-guo, CHEN Huai, WANG Bo, et al. Seismic response of large-scale aqueduct with fluid-structure coupling[J]. China Civil Engineering Journal, 2005, 38(8): 67-73.

[6]Shin S, Lee W I. Finite element analysis of incompressible viscous flow with moving free surface by selective volume of fluid method[J]. International Journal of Heat and Fluid Flow,2000(21): 197-206.

[7]Filipovic N, Mijailovic S, Tsuda A, et al. An implicit algorithm within the arbitrary Lagrangian-Eulerian formulation for solving incompressible fluid flow with large boundary motions[J].Computer Methods in Applied Mechanic and Engineering, 2006,195: 6347-6361.

[8]Souli M, Zolesio J P. Arbitrary Lagrangian-Eulerian and free surface methods in fluid mechanics[J]. Computer Methods in Applied Mechanic and Engineering, 2001, 191: 541-466.

[9]Henning B, Peter W. Arbitrary Lagrangian Eulerian finite element analysis of free surface flow[J]. Computer Methods in Applied Mechanic and Engineering, 2000, 190: 95-109.

[10]沈世钊, 武岳. 大跨度张拉结构风致动力响应研究进展[J].同济大学学报, 2002, 30(5): 533-538.SHEN Shi-zhao, WU Yue. Overview of wind-induced response for large-span tension structures[J]. Journal of Tongji University,2002, 30(5): 533-538.

[11]李遇春, 楼梦麟. 高排架渡槽风振的计算方法[J]. 同济大学学报, 2002, 30(2): 139-145.LI Yu-chun, LUO Meng-lin. Computing method of wind-induced vibration for tall-bent aqueduct[J]. Journal of Tongji University,2002, 30(2): 139-145.

[12]曾宪武, 韩大建. 大跨度桥梁风场模拟方法对比研究[J]. 地震工程与工程振动, 2004, 24(1): 135-140.ZENG Xian-wu, HAN Da-jian. A comparative study on simulation methods for wind field long-span bridges[J].Earthquake Engineering and Engineering Vibration, 2004, 24(1):135-140.

[13]李英民, 赖明, 赵青. ARMA模型及参数识别技术在脉动风仿真中的应用[J]. 重庆建筑工程学院学报, 1992, 14(3): 17-24.LI Ying-min, LAI Ming, ZHAO Qing. Application of ARMA model and parameter identification to simulation of pulsating wind[J]. Journal of Chongqing Institute of Architectural and Engineering, 1992, 14(3): 17-24.

[14]李春祥, 谈雅雅, 李锦华. 基于 ARMA模型模拟高架桥的脉动风速时程[J]. 振动与冲击, 2009, 28(6): 46-59.LI Chun-xiang, TAN Ya-ya, LI Jin-hua. Simulation of fluctuating wind speed time series applied on over pass bridges with resorting to ARMA model[J]. Journal of Vibration and Shock,2009, 28(6): 46-59.

[15]GB 50009—2001, 建筑结构荷载规范[S].GB 50009—2001, Criterion of architecture structure load[S].