基于高阶累积量实现数字调相信号调制识别

孙钢灿 王忠勇 刘正威

（郑州大学信息工程学院，河南 郑州450001）

引 言

通信信号调制识别是认知无线电的重要组成部分，一直是研究热点和难点［1－11］。基于统计量特征值的方法是调制识别领域的重要研究方向，Nandi［5］使用2阶矩特征值实现调制识别，Dobre［4］总结了基于2、3和4阶矩特征值的调制识别方法。高阶累积量相对高阶矩具有抑制高斯噪声的优点，张贤达［12］对累积量的计算和性质进行了研究。Swami［6］应用累积量特征值分类常用数字通信信号，陈卫东［7］和Hsiao－Chun［9］研究了基于4阶累积量的抑制多径干扰的调制识别方法，冯祥［8］提出一种将1个4阶累积量值和1个6阶累积量值相结合的调制识别方法，Orlic［10－11］提出了基于1个6阶累积量值的调制识别方法。这些研究表明：高阶累积量相对于高阶矩具有抑制高斯噪声优点。

本文介绍了基于高阶累积量构造调制识别特征值的方法，推导出了该特征值抑制多径干扰性能的一般表达式，证明累积量阶数越高，特征值抑制多径干扰的性能越好。基于此原因，提出了完全基于6阶累积量的调制识别分类特征值，给出了进行MPSK信号调制方式识别的方法。试验证明：6阶累积量特征值的抑制多径信道干扰能力要远高于4阶累积量，抑制高斯噪声的性能4阶累积量要优于6阶累积量，通过分析试验数据给出了不同信道情况下4、6阶累积量分类特征值的选择方法。

1 基于高阶累积量的调制识别特征值抑制多径干扰性能分析

给出经过多径信道信号的数学模型；采用累积量值相除的方法，构造出消除信道特性影响的调制方式识别特征值；分析比较不同阶累积量特征值抑制多径干扰性能。

多径信道建模为有限冲激响应（FIR）模型，其冲激响应表示为

式中：信道FIR模型的阶数为L＋1；hi（i＝0，1，…，L）是滤波器的抽头系数。

在接收机匹配滤波器输出端得到的码元同步采样复信号序列表示为

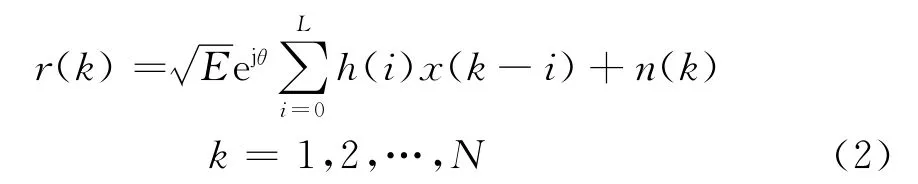
式中：x（i）为第i个发送码元序列，对MPSK信号x∈｛exp（j2π（m－1）／M｝，假设x（k）是独立分布的随机过程，且均值为0；h（i）为第i条路径的冲激响应；L＋1为多径数；n（k）是均值为零、方差为σ2的复高斯白噪声；N为观测到的码元个数；假设h（0）＝1，且为主径信道传输系数；E为主径信号平均功率；θ是未知的载波相位偏差。

设信号序列x（i）的p（偶数）阶累积量表示为cx，pq（l1，l2，…，lp），其中l1，l2，…，lp表 示 每个序列的时延值，q（q≤p／2）表示取共轭的序列个数。

考虑到发送码元序列x（i）是独立同分布的，所以其高阶累积量只有在l1＝l2＝…＝lp＝0时有非零值，此处令

利用高阶累积量函数的可加性质、高斯噪声高阶累积量值为零的性质，结合式（2）、（3）可得

式中：cr，pq表示过多径信道后序列r（k）的p阶累积量；l1＝l2＝…＝lp＝0；q为取共轭的序列个数。采用式（4）的累积量值，通过q值不同的两个累积量值相除，得到消除信道特性影响的调制识别特征值：

式中f为调制方式分类特征值。

从式（5）可以看出：只有1条路径时，多径数L＋1为1，信道的影响能通过取模后约去，也就是和没经过信道信号的特征值相等。当多径信道环境下，通过多径信道后的高阶累积量因为多径信道影响而不和调制信号发送序列的高阶累积量相等。原因是累积量表达式中取共轭的序列个数不同，多径信道对计算出的累积量值的影响表现为多个复数求和形式，取模后不再相等，多径信道将会对调制识别特征值计算结果产生影响。

同时可以观察到：式（5）中信道抽头系数hi的指数值和累积量阶数是相等的。假设最大径的冲激响应系数为1，其他径的冲激响应系数都要小于1.所以，当累积量阶数越大时，通过高次幂的运算，其他径相对最大径的值将变小。在满足时，可以忽略多径影响。

通过分析，比较累积量阶次不同带来的抑制多径性能不同。由矢量合成的性质可以得到

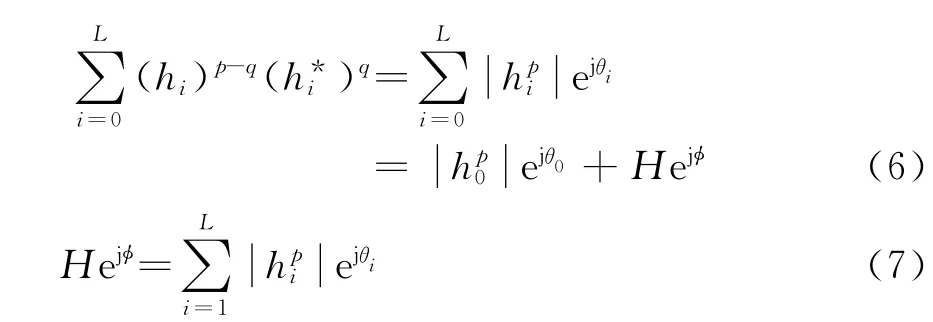
经过多径信道后接收信号的高阶累积量分类特征值等于发送端信号的分类特征值，而不受多径信道影响。

设存在常数R使得下式成立

表1 恶化最严重情况下多径信道幅度衰减系数取值

从上面的讨论可以看出：随着高阶累积量阶次的提高，抑制多径干扰的能力有了很大程度的提高。

上面讨论的是多径恶化最严重的多径信道情况，也是最严格的情况，实际多径信道每个径的幅度大小近似符合指数级数。设最大径幅度为次最大径幅度为为多径信道衰减系数，可得出下一径的幅度为其他径幅度按等比数列关系依次类推。设存在常数R使得下式

所以，为计算方便给出下式

化简后可得出

由无穷等比数列求和，可得出

当多径信道幅度按指数衰减时，根据R取值的不同，累积量阶数的不同，次最大径和最大径的关系如表2所示。

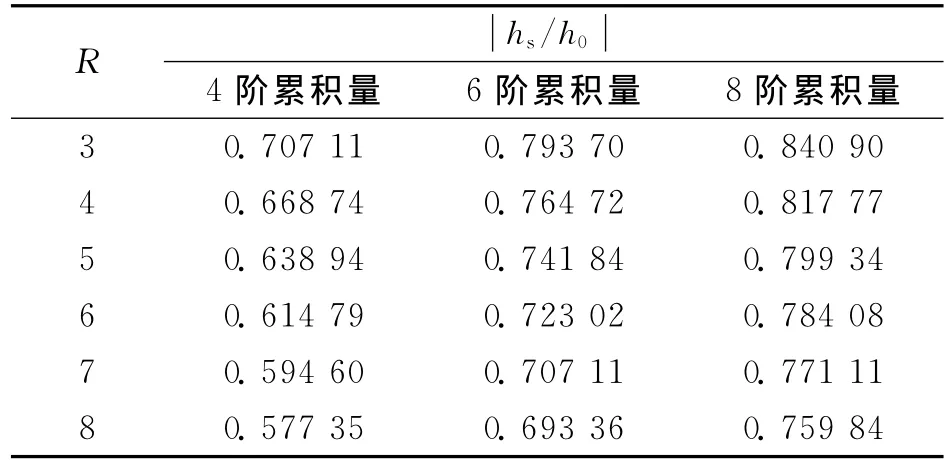
表2 指数衰减情况下多径信道幅度衰减系数取值

由表2可看出：在R值一定的情况下，累积量阶数越高，可处理的多径信道的次最大径幅度值越高。也就是说，在累积量阶数提高时，分类特征值的抑制多径干扰能力得到很大提高。

在实际应用中，可根据不同的多径信道衰减模型，来讨论高阶累积量调制识别的抑制多径干扰性能。

2 基于6阶累积量的MPSK信号分类特征值

上面推导证明了累积量的阶数提高可带来抑制多径干扰能力提高，下面通过一般意义上的累积量公式，结合MPSK信号相位分布，推导出MPSK信号6阶累积量计算公式。然后，根据每个累积量取值情况和方差大小，构造调制识别特征值，给出调制识别具体方法。

根据矩－累积量公式［12］

内求和。零均值复随机序列x（k）的6阶累积量表示如下

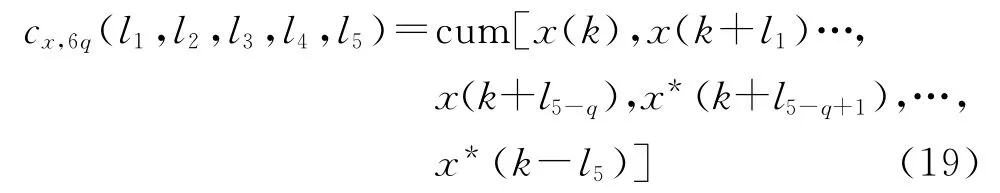
式中：cum［·］表示累积量计算表达；x＊（k）表示对序列求共轭；q表示其中取共轭的序列个数，当q＝0时，表示所有序列都不取共轭。

根据高阶累积量的性质，当所计算的序列独立同分布，高阶累积量只有在l1＝l2＝…＝lp＝0时有非零值，令cx，6q＝cx，6q（0，0，0，0，0，0）.由矩－累积量公式（18），可推导出以矩表示的6阶累积量表达式。对于零均值平稳复随机过程，奇数阶矩为零，因此，化简后得出以下结果。

式中：x（k）是零均值平稳随机序列；E［·］表示求数学期望。

在实际计算时，采用时间平均值来估计统计平均值。当待识别调制信号x（k）为MPSK信号时，累积量表征了其星座图分布情况。星座图为Aexp（j2π（m－1）／M），m＝1，2，…，M，M 表示调制阶数，取值为2，4，8等，A表示信号幅度。很容易得出不同阶数MPSK信号的高阶累积量值，如表3所示。

表3 MPSK信号的6阶累积量值

根据上面的取值情况，构造特征向量如下：

通过下面的试验证明：当信噪比恶化时cx，60的方差比其他6阶累积量方差大，抑制高斯噪声的性能相对比较差，所以式（24）中构造分类特征值没有采用它。对不同调制阶数MPSK信号，分类特征向量具有下列形式

选择分类器时，可以使用简单的欧式距离分类法，也可以用神经网络分类器。分类器的设计不是本文研究重点，所以此处采用简单直观的欧式距离分类器，判决准则为

式中：Fr＝ ［fr，1，fr，2］表示接收信号序列中提取的分类特征向量；Fr－FM2表示接收信号分类特征向量和待选择调制方式特征向量间距离。

3 计算机仿真

为了证明上面的理论推导结果，进行了算法性能仿真。待识别的调制方式为2PSK、4PSK、8PSK 3种，分别采用4阶累积量分类特征值［7］和上面推导出的6阶累积量特征值进行试验，从两个方面对两种方法进行了仿真分析。首先，进行两种方法的系统识别率试验，观察比较两种方法抑制多径性能和抑制高斯噪声性能；然后，计算信号和噪声的4、6阶累积量特征值的方差，分析比较两种方法抑制高斯噪声性能。

3.1 系统识别率分析

识别率试验中，试验数据为码元同步的复基带信号，长度为4 000点。将噪声和多径影响等效加载到基带信号上，信噪比为平均符号能量和噪声能量比的dB值。为方便观测实验结果，给出识别率曲线图1和图2，两图所代表的试验参数的范围不同，横坐标的含义也不同。

图1中，纵坐标为识别率，横坐标为信噪比变化情况。不同曲线类型分别代表4、6阶累积量算法的识别性能，曲线上的不同标注符号代表不同信道衰减系数取值。信噪比的范围为－5～20dB，每隔1 dB进行一次试验，多径信道幅度衰减系数值的范围为0.55～0.85，采用3径信道模型，多径幅度值按指数级数衰减，每次试验次最大径信道衰减系数值减少0.05，延时分别为［0、6、15］个采样间隔，相位值在0～2π内随机生成。3种PSK调制方式每种生成400组待识别数据，最后统计识别准确率。

通过图1可看出：识别率随多径信道衰减系数的减小而提高，同时随信噪比提高识别性能也不断提高。当采用6阶累积量时，信道衰减系数取值在0.85、信噪比大于2dB时，整体的识别率就可达到近85%.而同样情况下，4阶累积量的识别率只能达到70%.4阶累积量要达到85%以上的识别率，信道衰减系数的取值为小于等于0.75.从上面的观测结论可看出6阶累积量的抑制多径信道干扰能力强于4阶累积量，证明了理论推导结论。

从图1中低信噪比的区域可看出：在低信噪比情况下4阶累积量的性能优于6阶累积量。

图2中，纵坐标为识别率，横坐标为信道多径幅度衰减系数值。不同曲线类型分别代表4、6阶累积量算法的识别结果，曲线上的不同标注符号代表不同信噪比取值。信噪比的范围为－5～20dB，每隔5dB进行一次试验，多径信道幅度衰减系数值的范围为0.4～1，图中的每条曲线对应于不同的信噪比值，其他参数的设置同图1.

通过观察图1、图2看出：当信噪比大于5dB时，6阶累积量多径信道幅度衰减系数为0.75时，识别率可达到100%，通过式（17）可算出此时的R值是4.769 7。4阶累积量多径信道幅度衰减系数为0.65时，识别率可达到100%，此时的R 值是4.753 2.R值近似为5时，可认为累积量特征值可以克服多径信道对分类性能的影响。所以，在不同信道情况下，设计抗多径信道干扰的调制识别算法时，可根据表2选择所需分类用的高阶累积量阶数。

通过图2看出，4阶累积量在低信噪比情况下（符号信噪比小于等于0dB时）识别性能好于6阶累积量，当信噪比大于等于5dB时，6阶累积量的识别性能明显好于4阶累积量。这一方面说明了6阶累积量的抑制多径能力优于4阶累积量，验证了前面的结论；另一方面说明在低信噪比情况下，4阶累积量抑制高斯噪声干扰性能优于6阶累积量，下面通过特征值的方差分析造成这一现象的原因。

3.2 特征值的方差分析

虽然高阶累积量理论上可以完全抑制高斯噪声，但是由于试验数据长度有限，以时间平均值代替统计平均值必然带来偏差存在。高斯分布的随机噪声中，可能会出现幅度较大的复高斯噪声，当累积量阶数比较高时某些幅度较大的随机噪声值按幂运算增大，使得取均值之后仍然会比较大，因此，就会带来累积量值的偏差。当信噪比低于0dB时，这种现象会变得明显，信噪比越低时会变得越明显。因为是时间均值代替统计均值产生的，所以增加样本点数可以减小偏差值。

下面计算不同序列点数下噪声累积量值的方差，分析高阶累积量抑制复高斯噪声干扰能力。累积量的方差值代表了调制分类特征值的方差，决定了调制分类的精度，因此，这等于给出累计量的序列点数与调制识别性能的关系。

因为噪声序列和信号序列相互独立，由累积量性质可得出

式中：x（k）为信号序列；n（k）为复高斯噪声序列，二者相互独立。加上高斯噪声后序列的累积量等于相互独立的信号和噪声分别计算累积量的和。相互独立的随机变量和的方差等于方差的和，可得出

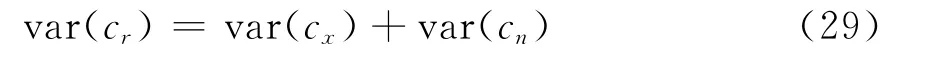
式中var（·）表示方差值。由于MPSK信号累积量的方差值一般比较小［6］，所以当信噪比较低时式（29）可近似表示为

通过试验，分别计算出MPSK信号的高阶累积量方差和高斯噪声的高阶累积量方差，表4、表5和表6列出了试验结果数据。

表4 MPSK信号累积量特征值的大样本方差（序列长度：4 000点）

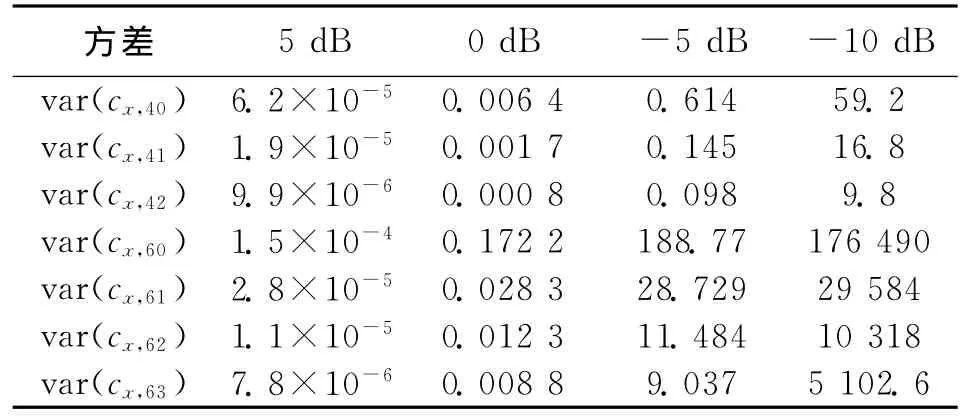
表5 高斯噪声累积量特征值的大样本方差（序列长度：4 000点）

表6 高斯噪声累积量特征值的大样本方差（序列长度：16 000点）

表4中列出的数值为MPSK信号4、6阶累积量值的方差，试验中，将MPSK信号幅度归一化，采样序列长度分别选择4 000点，仿真次数为1 000次，然后对这1 000个特征值求方差无偏估计值。

从表4可看出：在没有噪声干扰的情况下，2PSK在两种方法下方差值最优，近似为零。4PSK和8PSK信号都有些累积量的方差值较大，4阶累积量中var（cx，41）值较大（4.1×10－3），6阶累积量中var（cx，62）比较大（1×10－2），相比较4阶累积量的方差要小些。通过表3可看出cx，63的取值比较大，为4A6，cx，42取值为 A4［7］，由式（24）可知：由于分母比较大，应用6阶累积量可以使计算出特征向量的方差减小。通过上面的分析可看出：在没有高斯噪声干扰的情况下，4阶和6阶累积量分类识别特征值的方差特性近似。

表5和表6列出数值为复高斯噪声4、6阶累积量值的方差，试验中，将MPSK信号幅度归一化，根据信噪比值生成对应的复高斯噪声，计算复高斯噪声序列对应的累积量值，信噪比范围为－10～5dB，每隔5dB计算一次。采样序列长度分别选择4 000点和16 000点，仿真次数为1 000次，然后对这1 000个特征值求方差，var（cn）表示复高斯噪声累积量的方差。

通过表5和表6可看出：在信噪比等于5dB时，4阶和6阶累积量的方差都很小，说明此时取值比较稳定，不受高斯噪声的影响。当信噪比下降到0dB时，方差都有些变大，6阶累积量的方差要明显比4阶累积量大一个数量级，所以此时复高斯噪声已经比较严重地影响了特征值取值，而4阶累积量受到的影响相对较小。当信噪比降低到－5dB时，6阶累积量的方差取值很大，说明基本已不能完成调制识别，此时4阶累积量的方差也变大，说明其识别性能也受到很大影响。当信噪比降低到－10dB时，两种方式累积量的方差都很大。

通过比较表5和6发现：用于计算累积量的序列点数比较少时方差值大，这说明可通过增加序列长度提高抑制高斯噪声干扰性能，进而提高调制识别的准确率。

另外通过观察表中6阶累积量的方差发现，当信噪比恶化时，在4个6阶累积量值中var（cn，60）最大，说明cn，60抑制复高斯干扰的性能最差，所以，我们在式（24）中构造分类特征值 ［fx，1，fx，2］时没有选择cr，60.

3.3 试验结论

通过以上分析可看出：方差值观测结果和识别率观测结果是一致的。高阶累积量应用于MPSK信号调制识别时，抑制高斯噪声和抑制多径干扰的能力因阶数不同而不同。总体来说，阶数越高抑制多径干扰的能力越强，阶数越低抑制高斯噪声的能力越强。多径信道情况下，优先选择6阶累积量特征值。在信噪比较低（小于0dB）时，则要优先选择4阶累积量。根据以上原则，结合实际的信道情况决定如何使用。

4 结 论

进行MPSK信号调制识别时，使用消除信道特性影响的高阶累积量特征值可以抑制多径干扰。通过推导多径环境下信号的高阶累积量调制识别特征值通式，对不同阶累积量的抑制多径干扰能力进行了分析，分析结果显示累积量阶数越高抑制多径干扰能力越强。然后，推导出了MPSK信号6阶累积量特征值计算公式，给出了调制识别方法。最后，通过仿真试验证明上面推导出的结论。从试验结果看出：提高累积量阶数可以有效提高分类特征值抑制多径干扰的性能。但是，在低信噪比下，提高累积量阶数使算法抑制复高斯噪声的能力变差。分析了产生这一现象的原因，给出了不同信道环境下选择不同阶特征值的方法。

［1］吕铁军，魏 平，肖先赐.基于分形和测度理论的信号调制识别［J］.电波科学学报，2001，16（1）：123－127.LV Tiejun，WEI Ping，XIAO Xianci.Modulation recognition of signals based on fractal and measure theory［J］.Chinese Journal of Radio Science，2001，16（1）：123－127.（in Chinese）

［2］胡建伟，杨绍全，汤建龙.多径信道下 MPSK信号的调制分类算法［J］.电波科学学报，2005，20（4）：505－509.HU Jianwei，YANG Shaoquan，TANG Jianlong.Modulation classification of MPSK signals in multipath fading channel［J］.Chinese Journal of Radio Science，2005，20（4）：505－509.（in Chinese）

［3］李 鹏，汪芙平，王赞基.一种短波信道中数字信号调制方式识别算法［J］.电波科学学报，2007，22（5）：735－739.LI Peng，WANG Fuping，WANG Zanji.Algorithm for modulation recognition in shortwave channel environment［J］.Chinese Journal of Radio Science，2007，22（5）：735－739.（in Chinese）

［4］DOBRE O A.Survey of automatic modulation classification techniques：classical approaches and new trends［J］.IET Communications，2007，1（2）：137－156.

［5］NANDI A K，AZZOUZ E E.Automatic analogue modulation recognition［J］.Signal Processing，1995，46（2）：211－222.

［6］SWAMI A，SADLER B M.Hierarchical digital modulation classification using cumulants［J］.IEEE Transactions on Communications，2000，48（3）：416－429.

［7］陈卫东，杨绍全.多径信道中 MPSK信号的调制识别算法［J］.通信学报，2002，23（6）：14－21.CHEN Weidong，YANG Shaoquan.Algorithm for classification of MPSK signals in multipath channel environments［J］.Journal on Communications，2002，23（6）：14－21.（in Chinese）

［8］冯 祥，李建东.调制识别算法及性能分析［J］.电波科学学报，2005，20（6）：737－740.FENG Xiang，LI Jiandong.Modulation classification algorithms and performance analysis［J］.Chinese Journal of Radio Science，2005，20（6）：737－740.

［9］WU H C，SAQUIB M，YUN Z F.Novel automatic modulation classification using cumulant features for communications via multipath channels［J］.IEEE Transactions on Wireless Communications，2008，7（8）：3098－3105.

［10］ORLIC V D，DUKIC M L.Automatic modulation classification algorithm using higher－order cumulants under real－world channel conditions［J］.IEEE Communications Letters，2009，13（12）：917－919.

［11］ORLIC V D，DUKIC M L.Multipath channel estimation algorithm for automatic modulation classification using sixth－order cumulants［J］.Electronics Letters，2010，46（19）：1348－1349.

［12］张贤达.时间序列分析—高阶统计量方法［M］.北京：清华大学出版社，1996.