井筒套管对井间电磁成像测井信号传输的影响

陆 洪 刘 菊 陈林如

（中国电波传播研究所，山东 青岛266107）

引 言

井间电磁成像测井［1－5］是近年来发展起来的一种通过测量井间传播的电磁信号反演得到井间地层构造、储层和油、气分布的二维乃至三维的电阻率分布的方法，它是传统测井技术的重大发展。井间电磁成像测井是将低频电磁发射和接收阵列装置分别放置于2口已完钻的井中，发射信号的频率范围为5～1 000Hz，井间距离一般小于1km，通过改变发射天线和接收阵列天线在井中的深度，获得收发天线相对不同位置时，接收信号的幅度与相位的一系列测量值，然后根据这些测量数据，反演出井间地层导电率的空间分布。此种测井技术所用的发射天线一般采用绕制在坡莫合金做成的芯棒上的线圈，芯棒顺井筒垂直放置，接收传感器亦采用绕制在磁芯上的线圈，磁棒放置在垂直或水平方向接收磁场，由于测量距离远大于发射线圈与接收线圈的尺寸，故天线可理想化为磁偶极子。

很多钻井完钻后，为了防止坍塌，会加装井筒套管，套管的材质可能是钢质的，也可能是玻璃纤维的，加装套管，特别是钢质套管后，套管会对发射天线起屏蔽作用，使接收信号大为减弱，本文试图针对此问题定量地分析套管的材料、尺寸，以及测井工作频率对接收信号的影响。

1 问题的物理模型

为了使研究的问题能用解析方法分析，以及突出井筒套管对信号传输的影响，本文将所研究的物理问题理想化为如图1所示的模型。

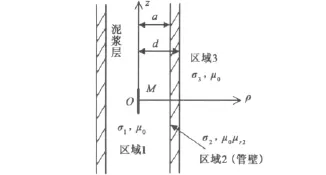
图1 井筒套管模型示意图

其要点是：1）地层的电导率分布是均匀的；

2）井筒的套管是无限长圆柱形；

3）发射天线是位于井筒中央ρ＝0，

z＝0处的垂直磁偶极子。在此物理模型下，区域1是井筒中的泥浆层，电导率记为σ1，磁导率为μ0，区域2是套管管壁，电导率记为σ2，磁导率记为μr2μ0，最外层是均匀地层，电导率记为σ3，磁导率为.

在此模型下，由于地层的旋转对称性，各个区域的电磁场仅有Hρ、Hz和Eφ三个分量，且它们应满足麦克斯韦方程。取时谐因子为e－jωt，电磁场用磁赫兹矢量位 Πm表示［6］，令

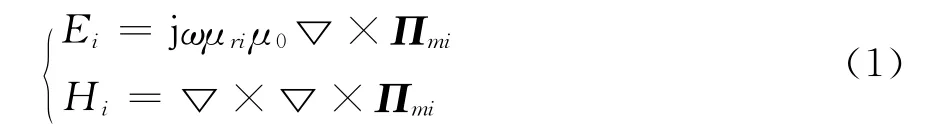
则赫兹矢量位Πmi在各个区域应满足赫姆荷兹方程

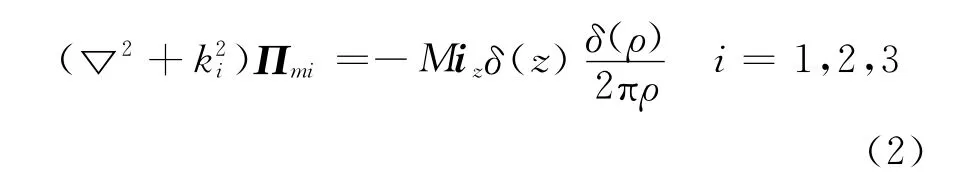
式中：M＝I·S·N是激励源的有效磁矩；S是线圈的面积；N为线圈有匝数；ki为电磁波在第i区中的传播波数，可以表示为

2 各个区域电磁场的解析表达式

在图1所示的物理模型下，由于方位的对称性，可以判断在各个区域，Πmi应仅有一个z分量，且它对方位φ是对称的。故可知，在此坐标下，电场和磁场可分别表示为

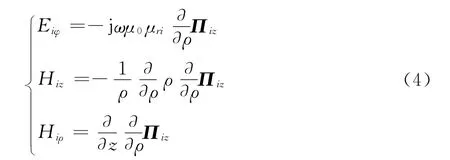
将拉氏算子▽2在柱坐标下展开，考虑到位函数对方位的对称性，式（2）可改写为

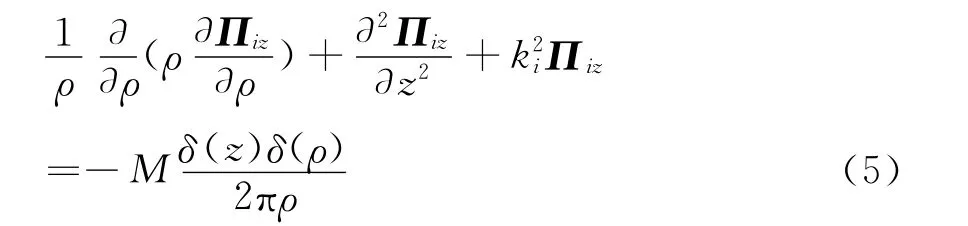
在区域2和3中，并没有场源，式（5）的右端应为0.令Πiz＝Z（z）Fi（ρ），代入式（5）分离变量后可得

式（6）中的解可取为e±jλz，因为Eiφ在各个区域的分界面上应连续，故位函数对z的变化应同步，故三个区域内位函数对z的变化都取一组。考虑到在区域1内，场源位于z＝0处，故在z＝0处，式（6）的右端应出现奇点，故可取

式（7）是典型的零阶贝塞尔方程，它的解应是圆柱函数。在区域3，ρ≥d，应该只有从井筒中激励场源产生的向外传播的电磁场，故应取

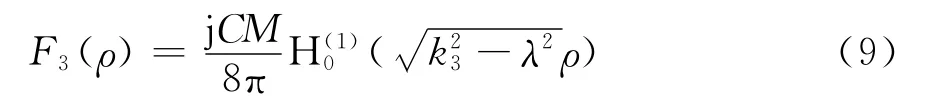
在区域2中，a≤ρ≤d，应同时有向外和向内传播的二个波，故可取

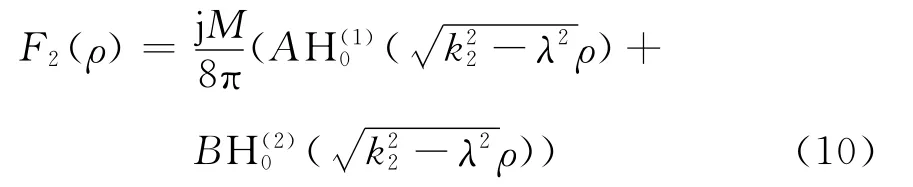
区域1包含场源，当观察点无限接近场源，套管及井筒外的介质对观察点的场应没有多大影响，此时位函数应接近于全部介质参数都与区域1中参数一样的均匀空间中的位函数。而均匀空间中磁偶极子产生的位函数已知为

当实际存在管壁和周围不同介质时，井筒内的电磁场除了场源产生的向外辐射场外，还应有由反射产生的局部场，故应取

由此，三个区域的电磁场位函数分别表示为

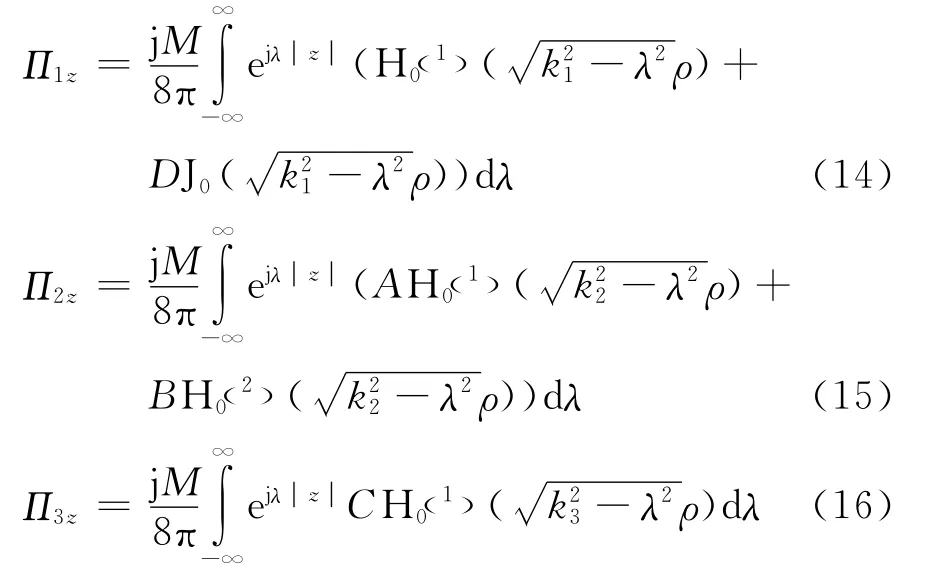
由此得出在各个区域的电场分量可表示为

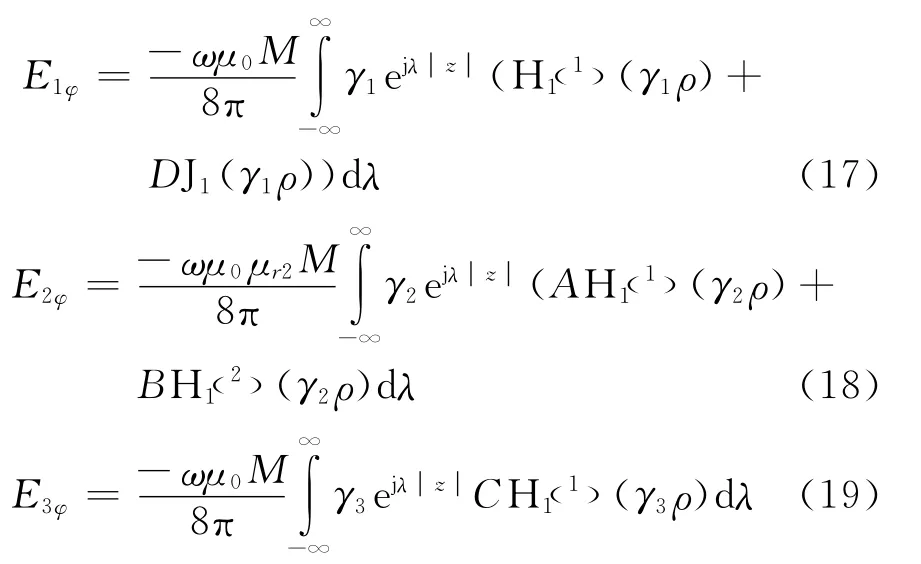
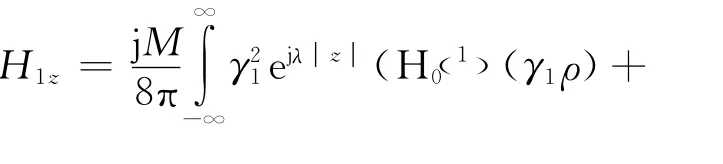
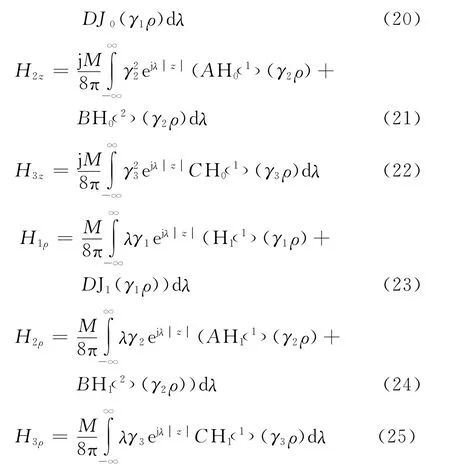
由分界面上Eφ和Hz的连续性可得

由式（27）和式（29）可解得

式中

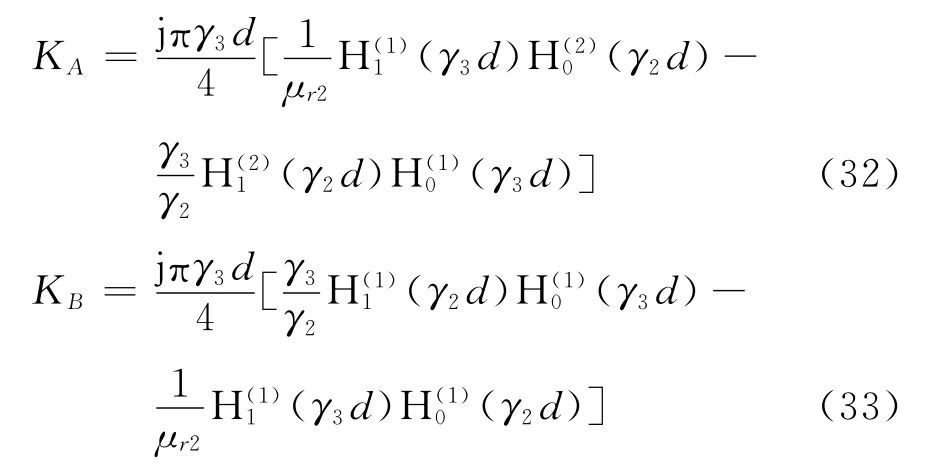
将式（30）和（31）代入式（26）和（28）可解得

式中

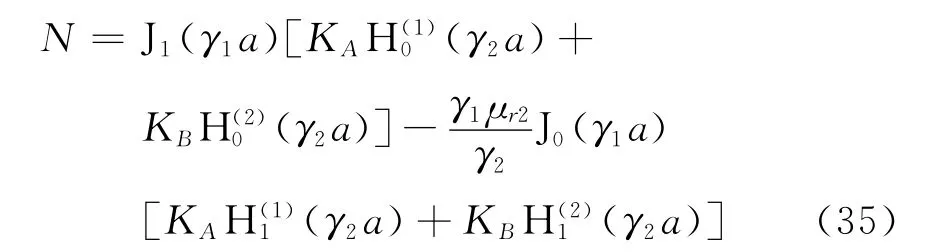
特别地当套管不存在，即区域2的媒质参数与区域3完全一样，即γ2＝γ3，μr2＝1，此时可看出，KA＝1，KB＝0.

3 套管外面场的分析讨论

井筒外面场的解析表达式已求出，由于地层是有耗介质，这些积分表达式实际上收敛都较快，可以用数值积分方法算出，在数值积分前还可做一些简化。首先因γi是λ的偶函数，且当λ是实数时，0≤argγi＜π／2，即在第一象限。故式（19）、（22）、（25）可分别改写为

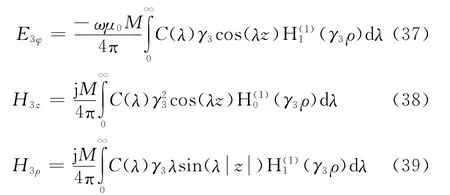
由于井筒一般较细，接收Eφ分量的电极无法放置在井筒内，实际中多选择接收Hz分量。以下计算中，如无特别说明，激励源的磁矩取M＝1 A·m2，接收天线位置z＝0m，井筒内一般填充有泥浆，电导率取σ1＝0.1S／m，地层电导率取σ3＝0.01S／m，取套管外半径d＝0.1m.

3.1 套管壁厚的影响

假设套管是钢制的，取σ2＝5×106S／m，μr2＝2 000.图2为频率10Hz，管壁厚度不同时，Hz的幅度与相位随距离的变化。

从图2可以看出管壁越厚，场强的衰减越大，管壁厚度每增加5mm，Hz的幅值大约减小27.03 dB，比平面波通过厚度为5mm的均匀介质的衰减e－0.005α2（－27.3dB）略小；在钢制介质中10Hz电波的波长为10mm，即管壁厚度每增加5mm，电波的相位变化180度，从图2（b）可以看出情况正是如此。

3.2 套管材质的影响

图3为套管材质不同时，Hz的幅度随距离的变化曲线，玻璃钢的电导率为10－4S／m，相对磁导率取1，铝的电导率为3.5×107S／m，相对磁导率也为1，裸井时，即认为σ2＝σ3＝0.01S／m，μr2＝μr3＝1.

从图3可以看出，套管为玻璃钢与裸井差异不大，信号几乎无衰减地通过，铝的屏蔽效果比钢小，比玻璃钢大。即在信号频率相同的情况下，套管对信号的屏蔽取决于套管的电导率和磁导率。

3.3 工作频率不同时场的分布

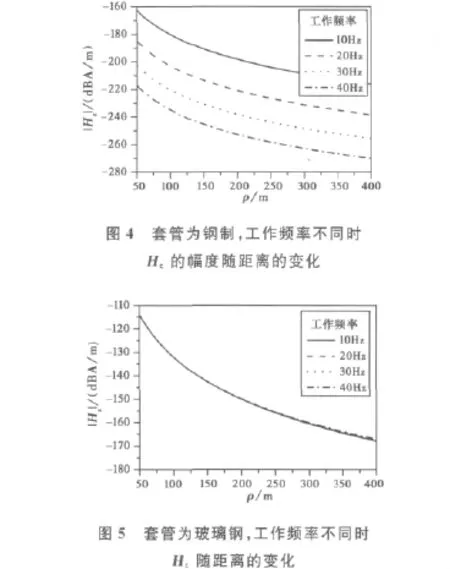
假设套管是钢制的，取σ2＝5×106S／m，相对磁导率μr＝2 000.图4为工作频率不同时，Hz的幅度随距离的变化。

假设套管是玻璃钢的，取σ2＝10－4S／m，相对导磁率μr＝1.图5为工作频率不同时，Hz随距离的变化。

从图4和图5可以看出有钢制套管时，频率高吸收大，裸井或玻璃钢管在400m范围内，因为是近区准静场，即k3ρ≤1，场的幅度与频率无关。

4.4 地层电导率

假设套管是钢制的，取σ2＝5×106S／m，相对磁导率μr＝2 000.图6为频率10Hz，地层电导率σ3不同时，Hz随距离的变化。

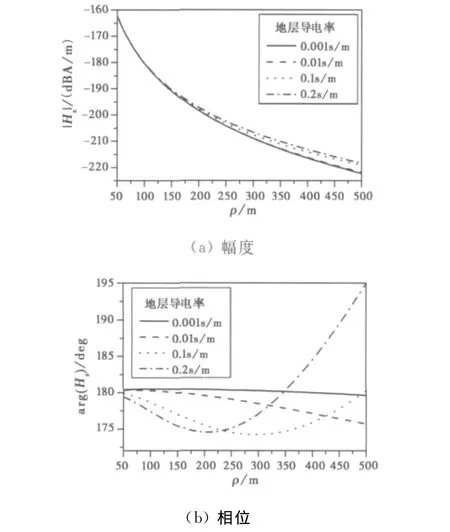
图6 套管钢制，地层电导率不同时Hz随距离的变化

从图6可以看出，随着地层电导率的增大，Hz的幅度增大，但地层电导率在0.001～0.2S／m变化，距离在500m范围内幅度的差异不是很明显；相位与地层的电导率密切相关，可通过幅度与相位的总体变化，确定地层的电导率。

4 结 论

将发射天线看作位于无限长圆柱形井筒套管中央的垂直磁偶极子，建立了井间电磁成像测井信号传输的三层模型，井筒套管内外是分布均匀的柱状介质，把电磁场用磁赫兹矢量位表示，推导了各个区域的电磁场积分表达式。最后用数值积分计算了不同情况下的电磁场分布，分析了套管电导率、厚度及测井工作频率对测井信号幅度与相位的影响。得出以下结论：

1）套管对测井信号的屏蔽效果取决于套管材质的电导率与磁导率，应尽量选择二者都小的材料，如玻璃钢；

2）井筒套管壁厚的增加会增加对信号的屏蔽作用；

3）铁磁性材料套管对高频信号的衰减较大；

4）可从接收信号的幅度和相位中提取出地层的电导率信息。

［1］宋汐瑾，党瑞荣，董 昭.套管井电磁测井技术及套管影响规律研究［J］.测井技术，2010，34（2）：143－145.SONG Xijin，DANG Reirong，DONG Zhao.On Electromagnetic logging technology in cased hole and its casing influence［J］.Well Logging Technology，2010，34（2）：143－145.（in Chinese）

［2］曾文冲，赵文杰，臧德福.井间电磁成像系统应用研究［J］.地球物理学报，2001，44（3）：411－422.ZENG Wenchong，ZHAO Wenjie，ZANG Defu.Application research of crosshole electromagnetic tomography［J］.Chinese Jounal of Geophysics，2001，44（3）：411－422.（in Chinese）

［3］杨 阳，党瑞荣，宋汐瑾，等.基于套管井中电磁测井响应的研究［J］.石油仪器，2009，23（5）：1－3.YANG Yang，DANG Ruirong，SONG Xijin，etc.Research on the electromagnetic logging responses in the cased hole［J］.Petroleum Instruments，2009，23（5）：1－3.（in Chinese）

［4］张 旗，杨善德.井间电磁成像技术中磁场振幅和相位的响应函数分析［J］.吉林师范大学学报：自然科学版，2009（2）：6－8.ZHANG Qi，YANG Shande.Detecting sensitivity and response functions analysis of crosswell electromagnetic tomography［J］.Journal of Jilin Normal University：Natural Science Edition，2009（2）：6－8.（in Chinese）

［5］梁秋锦，魏宝君.井间电磁成像方法的最新进展［J］.油气地质与采收率，2002，9（3）：63－66.LIANG Qiujin，Wei Baojun.Recent progress on crosshole electromagnetic imaging methods［J］.Petroleum Geology and Recovery Efficiency，2002，9（3）：63－66.（in Chinese）

［6］潘威炎.长波超长波极长波传播［M］.西安：电子科技大学出版社，2004.