自由空间导线天线辐射模式分析

余飞群 叶尚福

（盲信号处理重点实验室，四川 成都610041）

引 言

自Hertz 19世纪末创立天线理论以来，获得天线辐射细节一度成为天线研究的热点［1］。天线辐射过程通常与已建立的传输线的传输过程进行类比，天线电流分布也因此成为主要研究对象，并认为是与天线辐射有关的非常重要的信息。继Hertz之后，Pocklington从细导线假设出发，建立导线天线电流满足的积分微分方程，并指出电磁波沿导线以光速传播，导线天线的电流分布近似为正弦分布；此后Hallen在此基础上将积分微分方程化为积分方程，并提出求解该积分方程的近似方法［1－2］；高速计算机出现以后，K.K.Mei和Harrington先后利用数值方法求解该积分方程，并提出天线电流求解的矩量法［3－4］。虽然由天线电流分布可以获得天线的诸多性能参数，包括阻抗、辐射方向图等，但电流分布并不能很方便地表征天线作为辐射器向空间辐射电磁波的清晰物理图像。

研究天线辐射特性的另外途径是将天线体表面作为边界条件，选择合适的坐标系直接对Maxwell方程进行求解。最初选择的是长旋转椭球坐标系［5－6］，该坐标系当偏心率接近于1时，退化为有限长度的导线段，而当偏心率接近于0时，退化为球坐标系，因而长旋转椭球坐标系具有一定的通用性。采用分离变量的方法，可将该坐标系下赤道面附近馈电的长旋转椭球天线外的场表示为无穷项椭球波之和的形式，求和式中每一项对应天线辐射的一个模式，不同的模式在天线上激励出不同模式的电流，同时向外空间辐射一定的能量，天线上的总电流等于主模及所有高次模激励出的电流的总和，而天线以外的场则是所有模式场共同作用的结果。Chu和Stratton关于天线辐射场椭球波展开的思想很好地描述了天线辐射的机制，但因椭球波函数计算上的复杂性以及矢量椭球波函数的非正交性，在实际中受到较少关注［7］。

依据中心馈电天线径向传播的特点，Schelkunoff选择球坐标系对双锥天线进行研究［1，8］。按照Schelkunoff的理论，电磁波首先沿天线双臂按照TEM（横电磁波）模式进行传播，到达天线末端后一部分电磁波继续向外传播，并分裂成众多高次球谐波，而一部分将因为端效应电磁波则被反射回来，在天线附近区域形成驻波。Schelkunoff关于双锥天线辐射过程的物理图像是非常清晰的。天线近场及辐射场按照球面波函数进行展开，不同的球面波函数在空间呈现不同的电磁场结构，同时与球面波函数相关的球贝塞尔函数及连带勒让德函数在数值上易于求解，因而天线辐射场球面波展开得到广泛应用。

虽然场的球面波展开法早在1935年由Hansen最先提出［9］，并且成功应用于平面波照射下导体球散射截面的计算［10－11］及电小天线相关性能指标，如天线增益和Q值的计算等问题。但通过解析的方法，仅能获得极其有限数量的问题的解。更多的时候，人们需要通过适当的近似，并借助于计算机，得到波型展开系数的近似值。而针对天线辐射这一特定问题，球面波展开法所能获得的定量结果仅限于电偶极子和磁偶极子等的辐射问题［12－13］，很少有文献给出实际天线辐射场球面模式定量分析结果。

将球面波展开法引入到自由空间细导线天线辐射场的分析中：首先按照矩量法一般方法，采用分段正弦基函数对细导线上的电流分布进行展开并采用迦略金法求解电流展开系数；同时因为分段正弦电流辐射场均具有严格的解析表达式，因而可进一步获得细导线天线较为准确的辐射场表达式；最后结合数值积分方法，得到天线辐射场的球面波型展开系数。以该方法为基础，论文定量分析了三种基本天线的辐射模式，包括偶极子天线、圆环天线以及螺旋天线，仿真结果表明：该方法在分析天线辐射特性方面是正确并有效的。

1 天线辐射场计算

任意弯曲导线可用多段长度很小的直线段进行近似，且在细导线天线近似下，导线天线电流沿天线轴向流动，因而任意弯曲导线天线电流可表示为

式中，s为沿导线的曲线坐标，分段数为N＋1（相邻两分段构成一对偶极子，偶极子总数为N），且

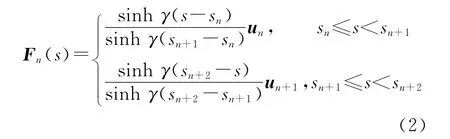
式中：γ＝j k，k＝2π／λ，λ为工作波长；un为第n段导线段切向单位矢量，且un＝（cosαn，cosβn，cosγn），其中cosαn，cosβn，cosγn为第n段导线段方向余弦。

按照式（1）给出的电流分布，第n段导线段实际上的电流分布为

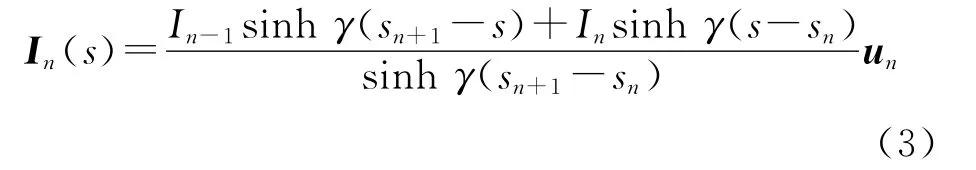
对于末端开路的实际天线，天线末端电流为零，有I0＝IN＋1＝0.

式（3）给出的电流分布在球坐标系下坐标为（r，θ，φ）处的辐射场为［14］

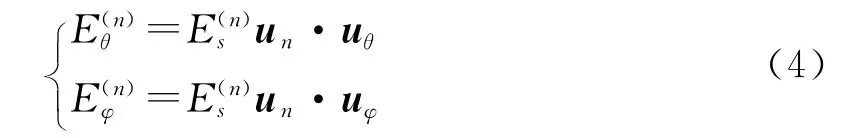
式中：

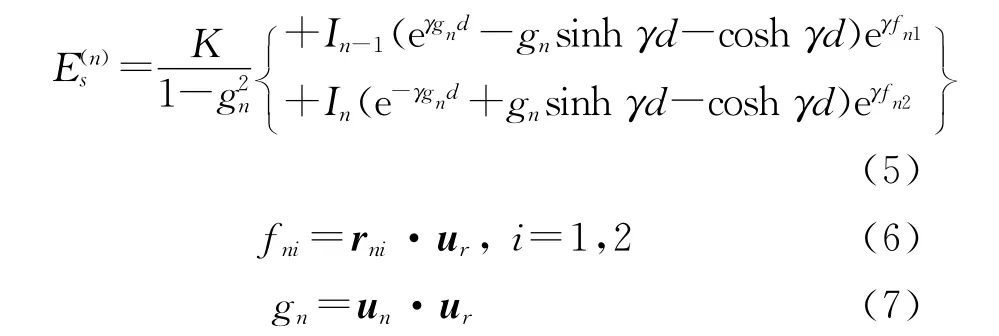
而 K＝ηe－γr／（4πrsinhγd），矢量rni＝（xni，yni，zni）为第n段导线段端点位置坐标。单位矢量ur，uθ，uφ为球坐标系坐标矢量。式（4）的辐射电场计算式中，未涉及任何对源点的积分，这也是正弦基相对于其它基函数，如三角函数基的优势所在。

式（1）中电流系数In由矩量法解得，按照式（4）并通过各分段正弦电流的场量叠加，可获得整个天线总的辐射电场表达式，天线总的辐射磁场可通过远区辐射场的辐射条件由总辐射电场计算得到。

2 场量已知时球面波展开系数的确定

对于第1章方法得到的E，H在某特定球面r＝r0以外的空间中的场，可用球矢量波函数 Mim，n，Nim，n表示为［10－11］

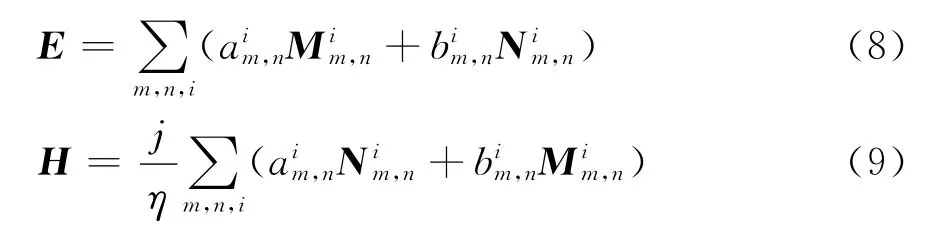
式中，r0可选为包含天线结构的最小球面半径，对于辐射场而言，r0可选为场点r坐标。矢量函数，满足

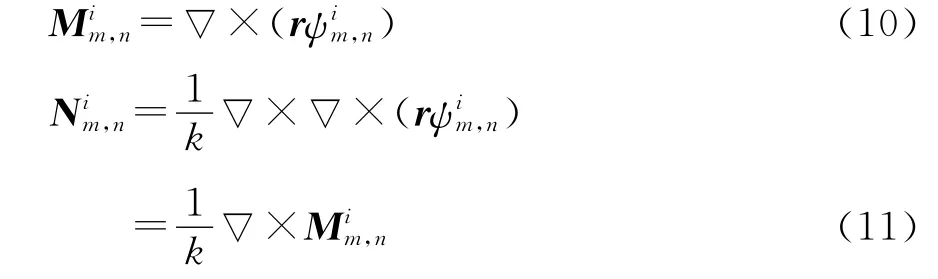
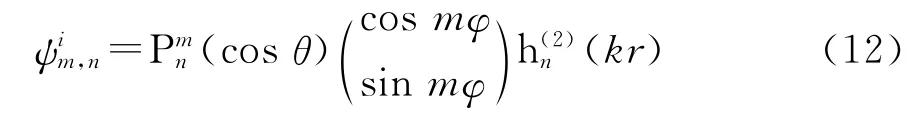
式中：i＝1，2，n＝0，1，2，…，m＝0，1，2，…，n.且i＝1时，式（12）取cos mφ，i＝2时式（12）取sin mφ；（cosθ）为连带勒让德函数；（kr）为第四类球贝塞尔函数。

若已知球面r＝r0上的切向电场Et（r0，θ，φ），则可分别以矢量波函数（r0，θ，φ），（r0，θ，φ）点乘式（8），并对整个r＝r0球面积分，同时利用矢量波函数的正交关系，最终计算得到系数为

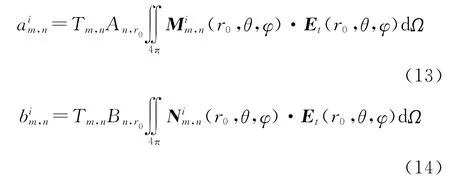
式中：

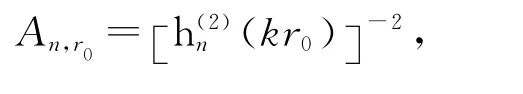
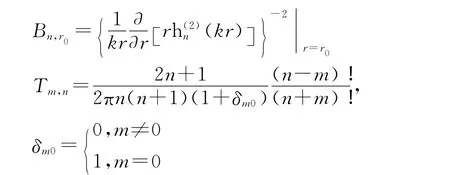
当已知球面r＝r0上的切向磁场 Ht（r0，θ，φ），可按相同方法得到展开系数的计算式。

3 实际算例及结果分析

将前两章所述方法应用于三种基本单元天线：偶极子天线、圆环天线以及螺旋天线的辐射模式分析。通过实际算例，验证球面波展开法在研究天线辐射特性分析方面的有效性。三种基本单元天线空间位置如图1所示。

图1 三种基本单元天线示意图

3.1 偶极子天线

考虑双臂总长为2L的直偶极子天线情况。偶极子天线轴线与球坐标系下θ＝0重合，导线中心位于坐标原点。此时天线辐射场与φ无关，辐射场电场的切向分量仅含Eθ分量，天线r＝L以外空间的场仅含模，因而＝0，仅需按式（14）计算系数

为验证计算方法及计算程序的正确性，采用类似的方法对r＝r0天线的近场进行球面波展开系数的计算。其中近场由各分段正弦电流产生的严格近场表达式通过场量叠加获得［12］。近场展开时，选择切向磁场Hφ作为展开对象，并按式（16）计算系数

表1给出了L＝0.25λ，导线参数Ω＝15（其中Ω＝2ln（2L／a），a为导线半径），r0分别取L，2L 时，式（14）计算得到的系数以及r0＝100λ时，式（16）计算得的系数.由表格1数据可知，不同球面半径下得到的近场的各模式展开系数相同，同时与辐射场球面波展开所得结果吻合较好。由于偶极子天线馈源附近切向电场相对于θ对称，这要求球面波展开各项为θ的奇函数，天线馈电区及近场区所有偶次模系数为零［1］，表1的计算结果证实了这一点。

表1 采用不同方法得到的系数

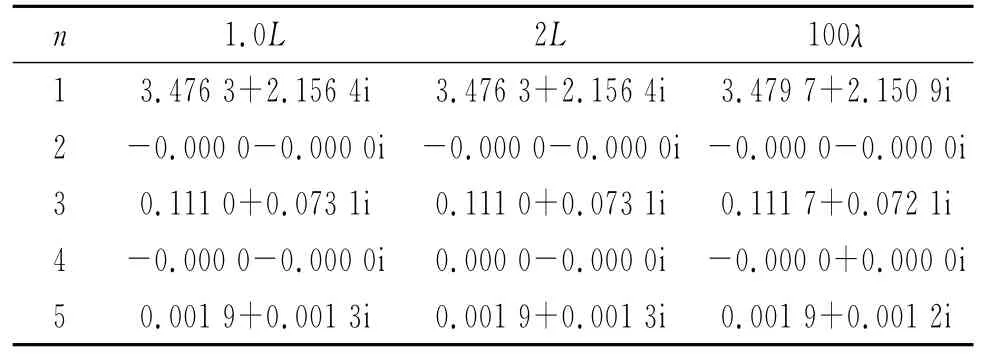
表1 采用不同方法得到的系数

n 1.0L 2L 100λ 1 3.476 3＋2.156 4i 3.476 3＋2.156 4i 3.479 7＋2.150 9i 2 －0.000 0－0.000 0i －0.000 0－0.000 0i －0.000 0－0.000 0i 3 0.111 0＋0.073 1i 0.111 0＋0.073 1i0.111 7＋0.072 1i 4 －0.000 0－0.000 0i0.000 0－0.000 0i －0.000 0＋0.000 0i 5 0.001 9＋0.001 3i 0.001 9＋0.001 3i 0.001 9＋0.001 2i

图2给出了r0＝100λ时，L分别取0.25λ，0.5λ，0.75λ和1.0λ时偶极子前6个奇次模系数模值曲线图。其中纵坐标含义为从图1可以看出，天线臂长不同，激励的各模式相对幅值不同。单就模来说，天线处于谐振状态（即L取0.5λ和1.0λ）下激励出的模式幅值明显小于非谐振状态激励出的模式幅值。谐振状态下，激励出的主模为模；对于臂长为1.5λ的偶极子天线，激励出的主模为模，且n＞3后各模式幅度随n增大迅速减小；而对于臂长2.0λ的偶极子天线模以后，幅值超过，n＞5后各模式幅度随n增大迅速减小。偶极子天线能够激励出的模式类型与导线上天线电流分布的振荡半周期数有关［1］，如果要激励出幅值显著的更高模式的球面波，则需要天线电流振荡半周期数增加到相应数值，天线将需要做得更长。图1给出的结果与文献［1］理论吻合。

3.2 圆环天线

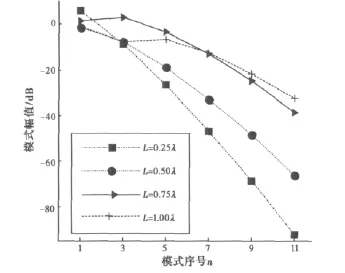
图2 不同长度偶极子天线TM10，n模式系数值

作为第二个例子，以环半径为b，导线半径为a的圆环天线作为研究对象。圆环位于xy平面内，中心与坐标原点重合，馈电点位于圆环上φ＝0处。为使获得的导线电流能真实反应圆环的轴向电流，取参数Ω＝2ln（2πb／a）＝15.由于圆环结构上的对称性，电场分量Eφ关于φ＝0，π和θ＝π／2对称，而分量Eθ则关于φ＝0，π和θ＝π／2反对称。又由矢量波函数，关于θ，φ 的对称性质及积分式（13）、（14）知当i＝1且n－m 为奇数时有非零值；当i＝2且n－m为偶数时有非零值。

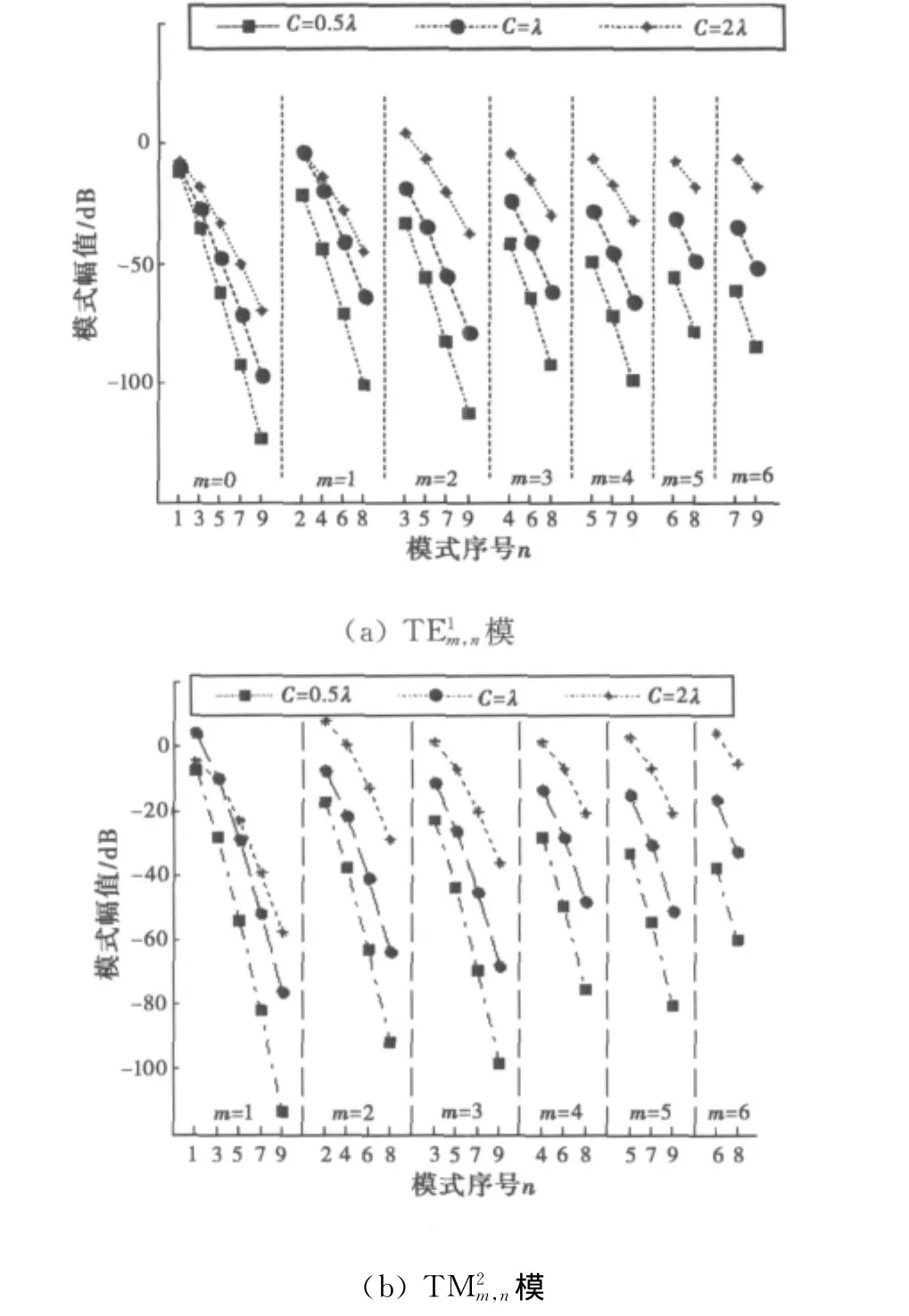
图3 不同周长圆环天线各模式系数值

图3（a），图3（b）分别给出了圆环周长C＝2πb取0.5λ，1.0λ和2.0λ时，圆环天线激励出的各模式幅度曲线图。与上面初步分析结果一致，圆环天线能够激励出的模式仅含有及.对于固定的m，各模式幅度随n增大而减小，且天线尺寸较小时，幅度模值随n增大衰减更快。对于固定的n，不同的圆环周长C激励出的主模有所不同。如C＝0.5λ激励出的主模为和；而对于C＝1.0λ激励出的主模则为和；而对于C＝2.0λ激励出的主模变为为和.主模出现以后的各模式幅度随m增大而减小。对于不同的圆环周长，大部分相同模式号的模式对应的幅度随C减小而减小，对于高次模这种变化趋势更为明显。

3.3 螺旋天线

自由空间的中馈螺旋天线被认为是一种阻抗和增益随频率高敏感的天线结构［15］，需谨慎选择天线结构参数。本节对文献［15］中工作在不同模式下的两种螺旋天线结构按照前述方法进行辐射模式分析，两种螺旋天线的结构参数摘录如表2所示。

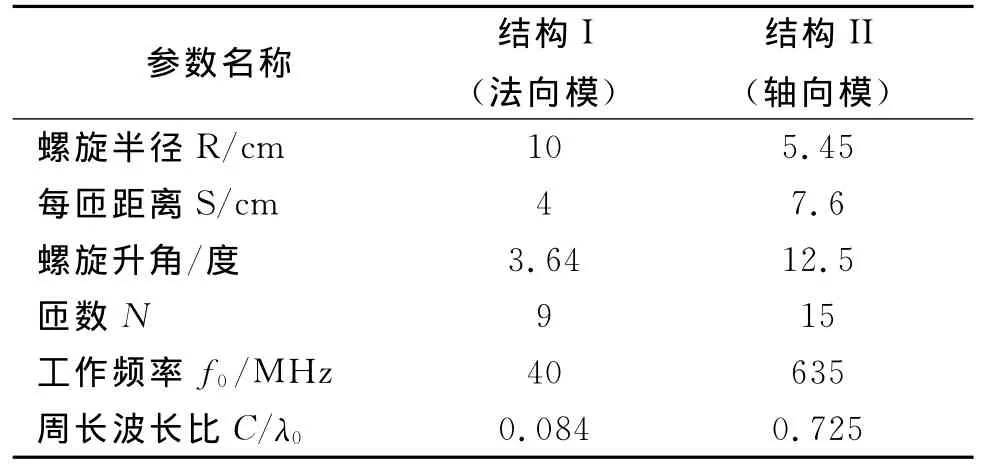
表2 用于仿真的螺旋天线结构参数

图4（a），4（b）给出了工作在法向模下的螺旋天线激励出的辐射模式。在这一特定结构下，辐射的模式主要以和为主，这些模具有水平面全向特性。对于给定的m，模式的幅度大部分随n－m增加而迅速降低，但也存在部分模式的幅度，如和，m＞1在达到一个 峰值后 再随n－m增加而减小。而对于给定的n－m，大部分模式幅度随m的增加而减小。

图5（a），5（b）给出了工作在轴向模下的螺旋天线激励出的辐射模式。对比图4（a），4（b），工作在轴向模下的螺旋天线其辐射的模式类别远比法向模丰富。在本例这一特定天线结构下，各模式幅度在量级上差别并不是很大，天线的几个主要模式存在于m＝1时。对于给定的m，大部分模式的幅度随n－m增加先达到一个峰值，然后再随n－m增加而迅速减小。对于给定的n，各模式的幅度随n－m增加而减小。这些规律与工作在法向模时的螺旋天线规律基本相同。

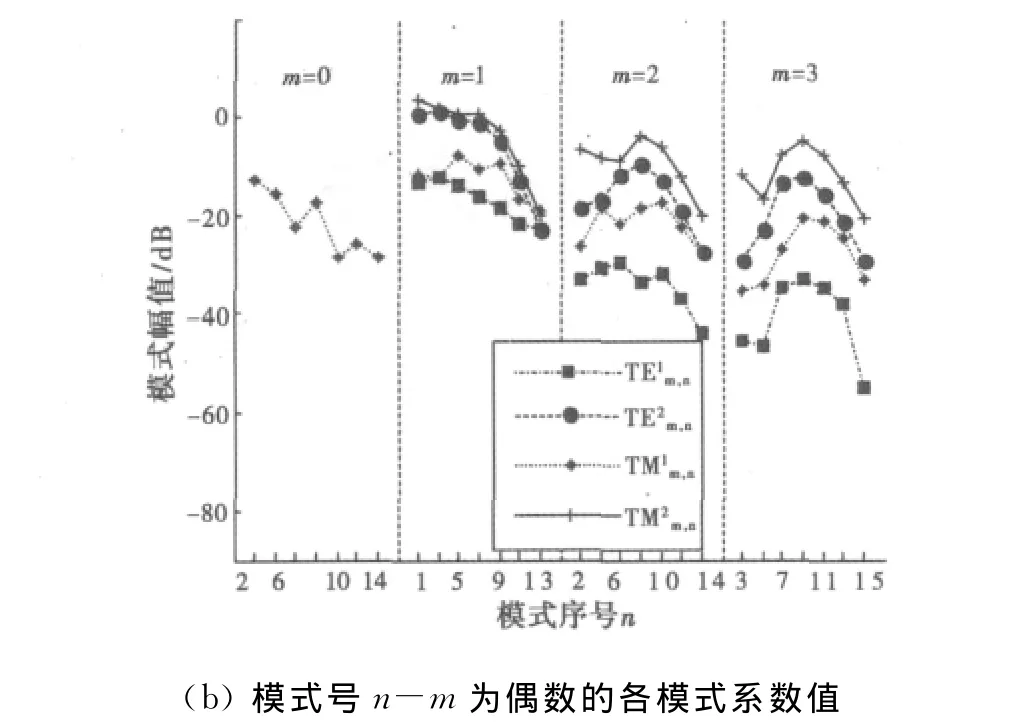
图5 工作在轴向模下的螺旋天线各模式系数值

4 结 论

虽然已知场量的球面波展开法很早之前已经提出，但很少有文献给出实际天线辐射场的球面模式分析的定量结果。论文利用由矩量法计算得到的天线辐射场，结合场量球面波展开的一般理论，将球面模式分析引入自由空间细导线天线辐射模式的分析中。利用数值积分方法，定量给出了三种基本单元天线：偶极子天线、圆环天线以及螺旋天线的辐射模式细节。从这三种基本单元天线的辐射模式的分析中，基本可以推断，导线天线电流在三维空间分布形式越复杂，电流分布具有的对称性越少，其辐射模式越丰富。

［1］SCHELKUNOFF S A.Advanced Antena Theory［M］.New York：Wiley，1952.

［2］李世智.电磁辐射与散射问题的矩量法［M］.北京：电子工业出版社，1985.

［3］MEI K K.On the integral equations of thin wire antennas［J］.IEEE Transactions on Antennas and Propagation，1965，13（3）：374－378.

［4］HARRINGTON R F.Matrix methods for field problems［J］.Proceeding of the IEEE，1967，55（2）：136－149.

［5］CHU L J，STRATTON J A.Steady－state solutions of electro－magnetic field problems III forced oscillation of aprolate spheroid ［J］.Journal of Applied Physics，1947，12（3）：241－248.

［6］PAGE L.The electrical osicllations of a prolate spheroid.paper III the antenna problem ［J］.Physical Review，1944 65（3－4）：111－117.

［7］LI L W，KANG X K，LEONG M S.Spheroidal Wave Functions in Electromagnetic Theory［M］.NewYork：John Wiley ＆Son，2002.

［8］SCHELKUNOFF S A.Theory of antennas of arbitrary size and shape ［J］.Proceedings of the IRE，1941，29（9）：493－521.

［9］HANSEN W W.A new type of expansion in radiation problems［J］.Physical Review，1935，47（2）：139－143.

［10］王一平，陈达章，刘鹏程.工程电动力学［M］.西安：西北电讯工程学院出版社，1985：271－273.

［11］STRATTON J A.Electromagnetic Theory［M］.New York：McGraw－Hill，1941.

［12］LI Lewei，WU Qun.Analytical form of EM fields radiated by circular aperture antennas of various current distributions［J］.Chinese Journal of Raido Science，2005，20（1）：1－7.

［13］MCLEAN J S.A re－exmamination of the fundamental limits on the radiation Q of electrically small antennas［J］.IEEE Transactions on Antennas and Propagation，1996，44（5）：672－676.

［14］RICHMOND J H.Radiation and scattering by thinwire structures in the complex frequency domain［R］.NASA CR－2396，1974.

［15］MAKAROV S N.Antenna and EM Modeling with Matlab［M］.New York：John Wiley ＆Sons，2002.