基于欠定盲分离的多目标微多普勒特征提取

郭琨毅 张永丽 盛新庆 沈蓉辉 金从军

（1.北京理工大学信息与电子学院电磁仿真中心，北京100081 2.航天系统仿真重点实验室，北京100854

引 言

目标或目标的组成部分的振动或转动会对雷达回波的频谱产生调制，这种现象称为微多普勒效应（Micro－Doppler Effect）［1］。目标回波中的微多普勒特征反映了目标的运动特征［2］、电磁特性以及几何结构特征。很多情况下，微多普勒特征可看成是目标的独一无二特性，微多普勒特征为雷达目标特征提取和目标识别提供了新的途径［3－5］，在雷达目标探测、分类、识别领域具有很大的应用潜力［6］。目前微多普勒特征的研究主要集中于单个目标，而对于回波中混叠了多个目标散射波的多成分微多普勒特征分析尚不多见。而研究多目标混叠回波中微多普勒特征的问题具有更重要的应用意义。例如，在弹道导弹突防中，往往会释放多个伴飞诱饵以掩护真弹头，实际接收的雷达回波中包含了多个目标的散射回波，显然，弹头和诱饵微多普勒成分的分离是识别真假弹头的必要且关键的问题。

目标微动特征探测一般采用非调制连续波雷达体制。非调制连续波雷达是目标测速的最简单、最有效的一种雷达模式，但仅适用于单一运动目标。在多目标场景下，连续波雷达接收到的回波中包含了多个目标的散射回波。从连续波雷达回波中分离出单个目标微多普勒成分，目前采用独立成分分析技术［7］，但该方法存在一定的局限性，首先，独立成分分析方法要求待分离的多个微多普勒特征之间必须是统计独立的；其次，分离计算时要求盲源信号构成的方程组是恰定或超定的，即观测到的混合信号的数目大于或等于待分离的未知源信号的个数。在实际应用中，由于观测条件有限，往往造成观测信号数目小于源信号数目的欠定情况，而且由于弹头和诱饵几何形状、散射特征相似，其微多普勒特征具有很大的相似性，独立性很难满足，因此，已有的分离方法不再适用。

为了解决上述问题，本文提出了一种基于欠定盲源分离（UBSS）［8－9］多种微多普勒特征的提取方法。该方法可以从少数原始雷达混叠回波中分离出多个目标的微多普勒特征，并且不要求微多普勒特征之间相互独立。给出了包含四个微动目标的仿真验证结果，为了保证回波数据精确性，采用全波数值算法［10］模拟回波信号。仿真结果证实了该方法的可行性。

1 多天线接收体制的回波模型

依据盲源信号分离的原理，本文采用最少数目的天线组成多天线接收体制，构造获得满足线性叠加性的原始混叠信号。考虑到弹头和诱饵散射中心较少，其回波的时频像数据多为稀疏矩阵，因而，本文选用基于稀疏表示的UBSS算法［8］实现多个独立微多普勒特征的提取。依据基于稀疏表示的UBSS方法原理，实现多个独立成分分离所需要的最少混合信号个数为3个，以3个天线接收体制为例，仿真构造原始观测信号，如图1所示。3个接收天线方向图相同，波束指向偏置，将其紧凑放置，使得3天线相对同一目标的雷达视线方向近似相同。

图1 三个不同方向图单脉冲雷达与多目标构成的雷达接收系统

依据基于稀疏表示的UBSS算法原理，混合信号要满足Xmixed（t）＝A×S（t），其中S＝ ［s（1），…，s（K）］∈Rm×K混合了m个未知的雷达回波源信号，A∈Rn×m为未知的混合矩阵，且m＞n，X＝ ［x（1），…，x（K）］∈Rn×K是雷达接收的可观察到的数据矩阵。利用改进的聚类算法将混合矩阵An×m从观测到的混合信号Xn×K中提取出来，再利用线性规划算法估计源信号Sm×K.建立雷达回波信号的模型。

为了便于理解，采用点目标模型表示N（N＝3）个天线接收到的M（M＝4）个扩展目标回波的混合信号模型，不考虑扩展目标之间的耦合，第n个连续波雷达一次跟踪时间T内所接收到的信号为

式中：Fnm（·）表示为天线的方向图加权，m＝1，…，M；sm（·）表示第m个扩展目标的回波

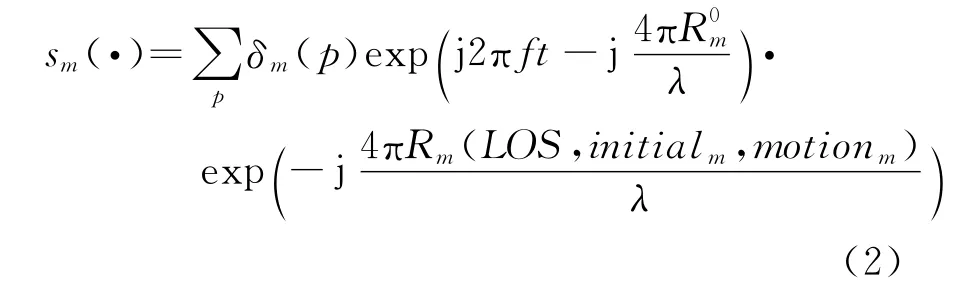
LOS 表示雷达的视线方向 （α，β）；δm（p）表示第m个扩展目标的散射中心的强度，initialm表示第m个目标的初始姿态角 （θ，φ，φ）；motionm表示第m 个目标的微动参数，包括角速度和轴线；R0m表示第m个目标微动参考坐标系与雷达之间的初始斜距；Rm表示第m个目标微动参考坐标系与雷达之间的斜距。

目标在不同雷达波束中位置的不同，造成了波束强度的差异，则N个不同方向图雷达波束照射下的多目标混叠回波可描述为

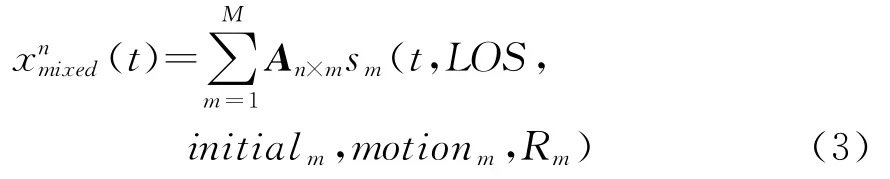
式中

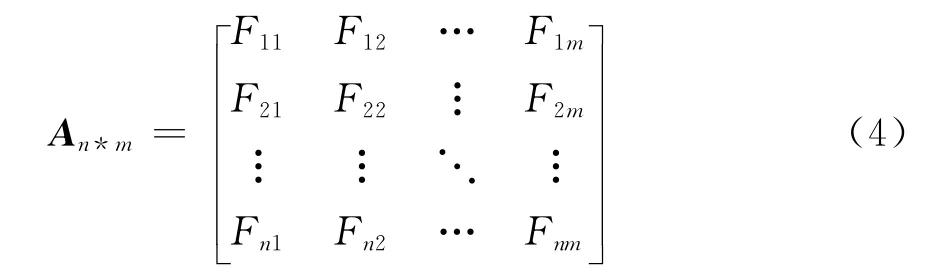
由基于稀疏表示的UBSS算法原理可知，实现独立成分分离的一个必要条件是混合信号为各成分的线性叠加。矩阵A表示的是不同方向图对于不同目标回波的幅度权值，在相对较小的观测时段内，平动造成的观测角变化很小，此时矩阵A与t无关，保证了此时段内混合信号与源之间的线性关系。通过欠定盲分离算法将矩阵A从N个天线接收的原始回波信号中提取出来，进而获得目标各自的微多普勒特征。

盲源分离算法无法得知分离信号的顺序，为了获知已分离的特征所对应的目标的方位，可以依据波束切换角测角原理，分别计算多天线中任意两天线差波束的回波信息，比较其与已分离的每个目标信号的相关性，相关性越小说明该差波束指向与此目标的实际方位越接近，调整天线波束指向，使得相关性最小，从而得到该目标的方位信息，此部分内容超出本文主要讨论内容，这里不再赘述。

2 基于UBSS多目标回波中独立成分的分离

基于稀疏表示的UBSS算法对源信号Sm×K的要求是源信号要满足一定理想的稀疏条件，即在Sm×K中存在大量只有一个元素不为零的列向量。如果源信号不满足此理想的稀疏条件，需要采用时频变换、小波包变换、快速傅里叶变换等处理方法将源信号变换成理想稀疏信号形式，分离处理后再反变换为原来信号形式。因为实际进动的弹头和摆动的诱饵的散射中心很少，而且微多普勒特征各不相同，因此，接收到的弹头和诱饵的回波经过时频变换得到的时频像具有比较高的稀疏性，基本满足基于稀疏表示的UBSS算法对源信号稀疏条件的要求，可以利用回波的时频像将各个目标的微多普勒特征成分分离出来。

设目标回波中包含四个目标，分别是一个锥旋进动的真弹头和三个摆动的诱饵，初始时间四个目标的姿态如图1所示。采用球头锥模型模拟钝头弹头结构，锥底和球头半径分别为0.5m和0.05m，弹头长1.6m，弹头质心位于距球头0.6m处，弹头底座与弹体之间为光滑弧形。由于球头锥为回转体，绕回转轴的自旋不会带来散射特征的改变，因此，可利用锥旋来描述圆锥体的进动特征［4］。设连续波雷达载频为3GHz，雷达跟踪时间为T＝1s，弹头锥旋频率为fc＝0.5Hz，半锥角为35°，锥旋轴Ac＝－Y1；诱饵1摆动频率为fs1＝3Hz，摆角范围8°，摆动轴＝－Y2；诱饵2摆动频率为fs2＝1.5 Hz，摆角范围10°，摆动轴＝－Y3；诱饵3摆动频率为fs3＝0.5Hz，摆角范围10°，摆动轴＝－Y4.仿真中A矩阵设为

Wigner－ville分布（WVD）是基于信号内积的Fourier变换［11］，文中采用 Reassigned SPWVD［12］方法对独立回波进行时频变换，得到的四个目标独立回波时频像如图2所示，而实际上3个雷达接收到的信号为目标回波的混合信号Xn×K，是3个混合了4个独立回波的混合信号，其时频像如图3（见图846页）所示，可看出3个混合回波的时频像中混叠了多个目标微多普勒成分，无法直接从时频像中获取目标的运动特性，必须进行分离。3个混合回波时频像的归一化幅值分布如图4所示。

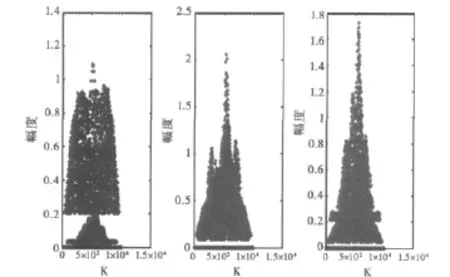
图4 混合信号时频像的归一化幅值分布图

根据基于稀疏表示的UBSS原理，第一步是要从混合信号Xn×K中找到混合矩阵An×m，依据是满足理想稀疏条件的源信号列向量中只有一个元素不为零的那些元素对应着混合矩阵的某一列。主要原理就是找出只有一个元素不为零的那些源信号列向量所对应的混合信号列向量并从中剔除频谱重叠的列向量，得到一系列行元素基本相同的子矩阵，然后将找到的子矩阵行平均化从而得到估计的混合矩阵，这里的混合信号Xn×K为3个天线回波的时频域数据。要达到此目的，首先去掉混合信号Xn×K中数值绝对值比较小的元素，即去掉每一行中元素小于某个数值η所对应的那一列，此步主要是去掉影响较小的元素，减少程序的计算量，则记剩余的矩阵为Xn×K1；然后再利用Xn×K1构造混合比率矩阵X′n×K1，取q∈ ｛1，…，n｝，具体步骤见公式（6）

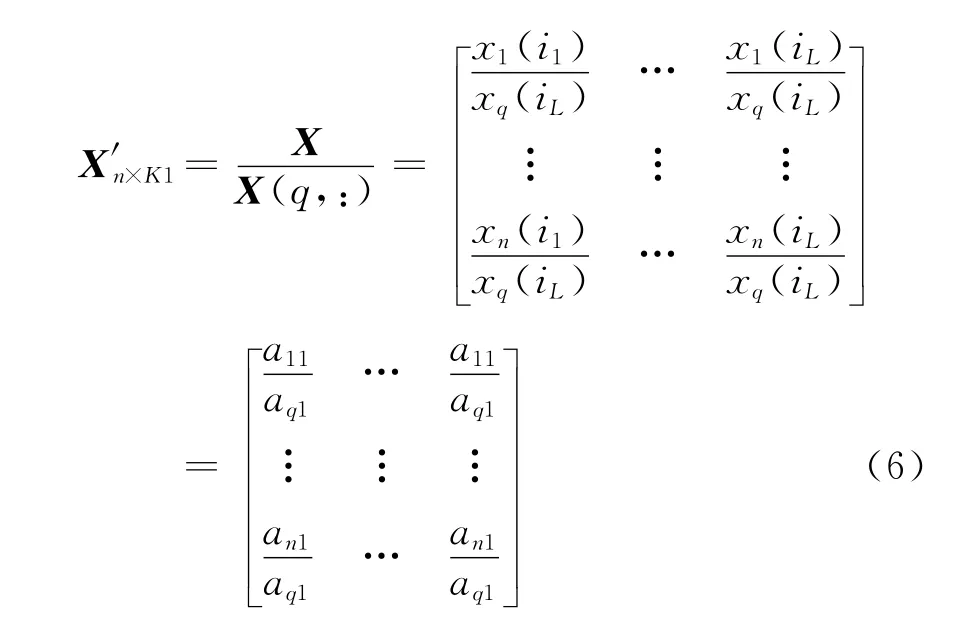
其中，L＝1，…，K1；最后利用聚类特性经过几次循环从混合比率矩阵X′n×K1中剔除重叠的频谱从而得到An×m的一个估计矩阵En×k，k＞n.经过多次参数调整第一次分离得到的估计矩阵为

第二步就是用线性规划算法估计源信号，根据所选UBSS算法原理，分离得到混合矩阵有6列，因此第一次分离得到的独立信号也是6个，分离信号的归一化幅值图和时频图分别如图5、图6所示。

图5 第一次分离得到的独立信号的归一化幅值图

对比图5、图6可看出（a）、（b）对应着同一个回波信号，（e）、（f）也对应着同样一个信号，而且E矩阵中一二列矩阵相同，五六列矩阵相同。所以去掉E矩阵中的第二、六列得到估计矩阵

图7 最终分离得到的分离信号归一化幅值图

由于算法原理需要经过几次循环，因而在此得到的估计矩阵A′中各列向量的顺序与文中选取的有差异，但是这并不影响分离结果。估计得到A′后，再一次应用线性规划算法估计源信号，得到的4个信号归一化的幅值图如图7所示，对应的时频像如图8所示。与未经混叠的4个独立目标回波时频像比较可见，经本文提出的基于欠定盲分离方法处理得到了4个目标独立的微多普勒特征。

3 结 论

针对目前已有的连续波雷达多目标回波中微多普勒特征提取方法的不足，本文提出了基于稀疏表示的欠定盲分离方法。该方法从盲源分离原理出发，利用多天线接收体制获得多个原始混叠信号，再利用目标回波时频像的稀疏性，采用基于稀疏表示的欠定盲分离算法提取回波中多种微多普勒特征。该方法突破了已有算法对原始混合信号个数必须大于或等于目标个数以及各目标微多普勒特征之间必须满足统计独立性的限制，实现了利用较少的接收天线分离出多个目标的微多普勒特征。文中给出了该方法的数学原理、实现流程和仿真实例，验证了该方法在处理欠定情况下连续波雷达回波中微多普勒特征提取问题的有效性。

［1］CHEN V C，LI F，HO S S，et al.Micro－Doppler effect in radar phenomenon model and simulation study［J］.IEEE Transactions on Aerospace and Electronic Systems，2006，42（1）：2－21.

［2］LEI P，WANG J，SUN J.Analysis of radar micro－Doppler signatures form rigid targets in space based on inertial parameters［J］.IET Radar Sonar and Navigation，2011，5（2）：93－102.

［3］GAO H W，XIE L G，WEN S L，et al.Micro－Doppler signature extraction form ballistic target with micro－motions［J］.IEE Transactions on Aerospace and Electronic Systems，2010，46（4）：1969－1982.

［4］GUO Kunyi，LI Qiao，SHENG Xinqing.Precise recognition of warhead and decoy based on components of micro－Doppler frequency curves［J］.Sci China Inf Sci，2012，55（4）：850－856.

［5］关永胜，左群声，刘宏伟.基于微多普勒特征的空间椎体目标识别［J］.电波科学学报，2011，26（2）：209－215.GUAN Yongsheng，ZUO Qunsheng，LIU Hongwei.Micro－Doppler signature based on cone－shaped target recognition［J］.Chinese Journal of Radar Science，2011，26（2）：209－215.（in Chinese）

［6］高红卫，谢良贵，文树梁.基于微多普勒特征的真假目标雷达识别研究［J］.电波科学学报，2008，23（4）：16－20.GAO Hongwei，XIE Lianggui，WEN Shuliang.Research on radar identification of ballistic missile warhead and decoys based on micro－Doppler signature［J］.Chinese Journal of Radio Science，2008，23（4）：16－20.（in Chinese）

［7］GUO Kunyi，LI Qiao，SHENG Xinqing.A precise recognition method of missile warhead and decoy in multi－target scene［J］.Journal of Electromagnetic Waves and Applications，2010，24（5／6）：641－652

［8］LI Y Q，AMARI S，CICHOCKI A，et al.Underdetermined blind source separation based on sparse representation［J］.IEEE Transactions on Signal Processing，2006，54（2）：423－437.

［9］PENG D Z，XIANG Y.Underdetermined blind source separation based on relaxed sparsity condition of sources［J］.IEEE Transactions Signal Processing，2009，57（2）：809－814.

［10］SHENG X Q，JIN J M，SONG J M，et al.On the formulation of the hybrid finite－element boundary－integral methods for 3Dscattering using multi－level fast multipole algorithm［C］／／IEEE Antennas and Propagation Society International Symposium，Atlanta，June 21－26，1998，46：303－311.

［11］陈 珺，闫 述，李正斌，等.联合时频分析在电磁测深问题中的应用［J］.电波科学学报，2003，18（4）：393－399.CHENG Jun，YAN Shu，LI Zhengbin，et al.Applications of joint time－frequency analysis methods in the geologic sounding［J］.Chinese Journal of Radio Science，2003，18（4）：393－399.（in Chinese）

［12］ANTONIA P S.Applications in time－frequency signal processing［M］.Florida：CRC Press，2003：16－33.