全球导航卫星系统反射信号几何关系数值分析
杨东凯 王 烨
(北京航空航天大学电子信息工程学院,北京100191)
引 言
利用全球导航卫星系统反射信号(GNSS-R)的遥感技术是近年来逐渐发展起来的一项新技术,是国内外遥感和导航技术领域研究热点之一。GNSSR技术以其大量、免费的信号源,不需发射机,体积和重量都较小,便于机载和星载使用等优点,引起了人们的重视和广泛应用。
GNSS反射信号的几何关系是实现反射信号遥感研究和应用的基础和前提,也是GNSS-R反演模型理论研究和应用的关键。建立完善可靠的几何关系模型有助于开展遥感应用中的地表特征探测、测高测距、风向和风速的反演等工作,同时,对GNSSR几何关系的研究有助于推进我国GNSS遥感技术的发展,开发具有自主知识产权的GNSS-R处理和验证系统,使其实现对反射信号进行码延迟和多普勒的二维搜索,以实现更精细的码延迟分辨率和多普勒分辨率。
目前对于GNSS-R遥感模型研究,主要是对L波段GNSS发射的经伪随机噪声码(PRN)调制的载波信号海面散射问题进行建模。Zavorotny等将这类问题看作基尔霍夫近似的几何关系模型(KAGO)[1],并对利用该模型下的全球定位系统(GPS)反射信号海面风场探测进行了较为系统的分析,但是文中并未对影响该模型的几何参量进行分析;Elfouhaily T等人对海浪谱模型进行了全面的描述,并阐述了不同海浪谱模型及模型中不同参数的选取对模型精度的影响[2];Thompson等提出了改进的几何光学模型并分析了几种模型间的相互关系[3];张东和等对GPS信号的多普勒效应进行了分析[11],但并未就时延和多普勒对反射区域的二维分割问题进行阐述。Fung等利用的积分方程法(IEM)模 型[4],Coatanhay 等 使 用 的 双 尺 度 模 型(TSM)[5],以及 Huai-Tzu You等人从随机过程角度进行的海面散射信号的模型分析[6]也为GNSS-R技术在测高、反演海态[7,13]、土壤湿度测量[8]、灾害探测[9]、反射信号模拟器设计[10]等具体应用中提供了可用的重要的分析模型。然而,这些模型的研究中主要侧重于信号及其在遥感具体应用中的可行性分析,缺乏对反射信号模型几何结构的系统分析和总结。文章旨在分析影响GNSS反射信号等延迟区和等多普勒区域变化的要素,计算各要素对GNSS反射信号几何关系的定量影响,为陆基、机载和星载的各类反射信号接收机的码延迟、多普勒分辨率及其有效作用范围提供设计依据。
1 GNSS反射信号等延迟区
GNSS反射信号的几何关系示意图如图1所示。

图1 等延迟区几何关系示意图
入射信号经过反射面散射后再进入接收机中,由于信号传播的路径不同,不同散射点对应的传播时间不尽相同。由镜面反射点的定义可知,由发射机T发出的入射信号经镜面反射点o反射到达接收机R所经过的距离最短,因此其传播时间也最短。为了方便研究,我们选取镜面反射点o为参考点,则沿这一路径的传播时间为
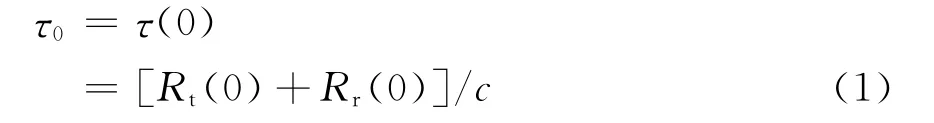
式中c为光在空气中传播的速度。
信号沿任意一条反射路径的传播时间可以表示为

以τ0为参考,定义其他路径上信号传播的时间与τ0的差值为时间延迟Δτ,即

反射平面上由Δτ等于常数的点组成的线称为等延迟线。而满足(k为不小于0的实数)的点组成的区域称为同一个等延迟区,一般情况下,等延迟区的形状为椭环。根据上述公式,等延迟线或等延迟环的形状和大小与接收机的高度、发射机(GNSS卫星)的高度角和方位角等因素有关。
1.1 不同卫星高度角下的等延迟线
设卫星高度为20 000km,接收机高度为5km,选取卫星高度角分别为30°、45°、60°和90°时,等延迟线的形状和大小如图2所示。其中,τc为C/A码的码元宽度。可以看出,随着时间的延迟,等延迟椭圆的中心将沿长半轴向发射机方向运动,仰角越低,椭圆越扁,沿发射机方向偏离镜面反射点的幅度越大。等延迟椭圆沿入射面方向(横轴)是对称的,但是等延迟椭圆以镜面反射点为中心,沿垂直入射面方向(纵轴)具有明显的不对称性,随卫星高度角的降低,这种不对称性逐渐增大,等延迟区域主要集中在发射机方向。在高度角较低(如30°)的情况下,第10个码片等延迟区中心沿发射机方向移动约10 km,这种较大不对称性说明散射信号主要来自于等延迟区的长轴方向,这使得风向的遥感探测成为可能[12]。
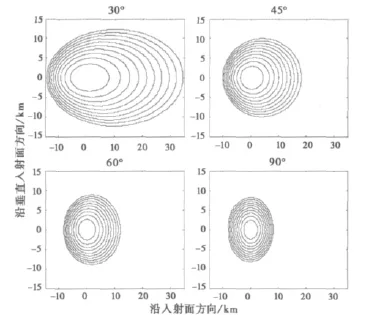
图2 不同卫星高度角下的等延迟线
1.2 不同接收机高度下的等延迟线
当设定卫星高度角为60°时,分别设定接收机高度为1km、5km和10km,通过计算可以看到不同接收机高度下的等延迟线变化情况,如图3所示。x轴表示沿垂直入射面方向,y轴表示沿入射面方向。可见,接收机的高度越低,等延迟区范围越小,从而反射信号的能量区域也就越小,能量越集中。
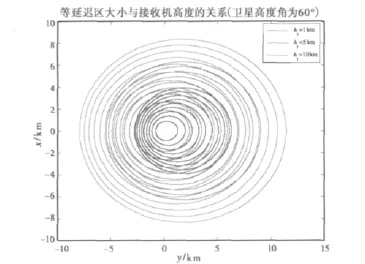
图3 不同接收机高度下的等延迟线
在上述的等延迟线计算过程中,可以清楚地看到随卫星高度角和接收机高度变化时,等延迟线的变化规律。对结果进行统计可以得出如图2所示的规律。表1和表2中分别列出了接收机高度为5 km和10km情况下,不同卫星高度角下的第1~10等延迟线的长轴长度。当接收机高度为5km,卫星高度角为90°时,第10个等延迟环的长轴长度只有12.32km,而同一接收机高度下,卫星高度角为30°时,第1等延迟环的长轴长度便达到10km.在相同接收机高度下,随卫星高度角的变化,等延迟区不仅存在方向上的偏移,其长轴长度、同一码片的等延迟环的大小也发生变化,卫星高度角越大,等延迟环越小。通过表1和表2还可以看到,同一卫星高度角下接收机高度对等延迟环大小的影响,接收机高度越高,等延迟环长轴长度越大。特别当接收机高度为10km,卫星高度角为30°时,第10个的等延迟环的长轴长度超过49km,接近一个风区的长度。根据PRN相关函数特点,其能量贡献区域主要来自采样时刻τc的等2个码片长度的延迟环带内,因此,当取10个等延迟环所覆盖的区域为一个单元时,可认为反射信号的能量几乎全部集中于该区域内,所以多个单元等延迟环的信号能量可认为来自不同的风区。这在海面风场反演的实际应用中具有重要意义。
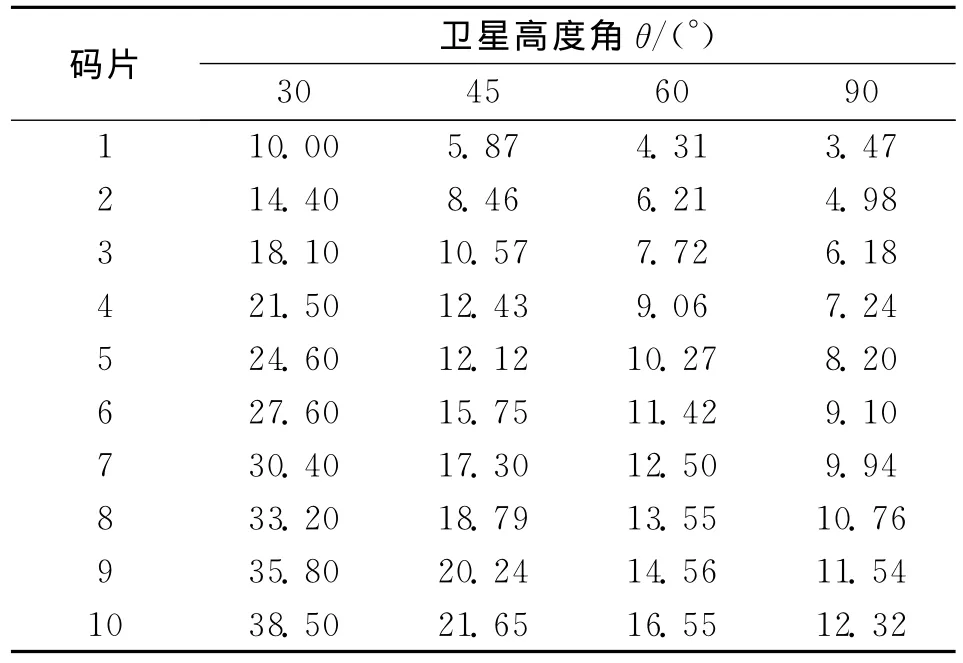
表1 接收机高度为5km,不同卫星高度角下第1~10等延迟环的长轴长度/km

表2 接收机高度为10km,不同卫星高度角下第1~10等延迟环的长轴长度/km
对海洋风场来讲,一个风区的长度一般是50 km,由于接收机的高度通常在几千米到十几千米范围内,等延迟区长轴长度与码片、卫星高度角密切相关。在低卫星高度角条件下(如30°),10个码片的等延迟区足以覆盖一个风区,而在高仰角条件下(如60°),可以通过使用更多码片(30~35个码片为宜)下的等延迟区来覆盖更大的范围。需要指出,对于海洋风场的风向和风速探测,感兴趣的部分分别是时延较大和较小的部分,因此,在实际遥感应用中可以根据不同的需要选取不同码片下的等延迟区域进行分析和处理。
对于某一特定的时延范围所形成的等延迟区,往往希望得到更加精细的距离单元,以达到较高的反演精度。此时,可以通过GNSS接收机对信号进行高速采样的方法来细化信号能量单元,提高距离分辨率。例如,采样速率fs=20.456MHz,则采样信号间隔τs=1/fs,对GPS C/A码而言,约τc/20,对应距离分辨率可达15m.
1.3 多颗GNSS卫星的等延迟线
在反射平面内,GNSS卫星方位角Φ以正北方向为0°,沿顺时针旋转增加。通过表1、表2及1.2节中的结论可知,对单颗GNSS卫星而言,在所设定的仿真条件下,第10个等延迟环的长轴长度不超过50km,远小于地球半径,因此,在机载接收机高度下反射面可视为平面,这一结论同样可以应用到多颗不同方位的卫星计算中。以4颗GPS卫星为例,图4显示出了接收机高度为5km时,不同卫星高度角和方位角下的等延迟线仿真结果,其中Δτ=[1,2,3…10]·τc.
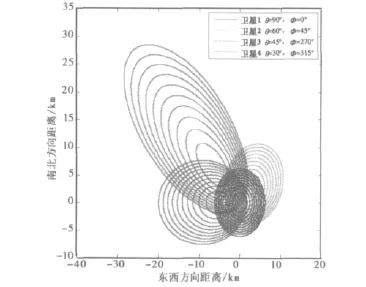
图4 多颗不同方位角/高度角卫星的等延迟线
由此可以看出,卫星方位角对等延迟线的形状和大小没有影响,只是改变其偏移的方位。不同的是多颗卫星下,只有卫星高度角为90°时,其镜面反射点与原点坐标重合。这是由于卫星高度角为90°时,接收机与发射机处在同一垂直于反射平面的直线上,且垂线与反射平面的交点恰为镜面反射点。其他卫星高度角下,镜面反射点的位置沿卫星所在方位各自发生偏移。且不同卫星的等延迟线存在交叠,交叠区域中的反射信号较其他区域的反射信号要强得多。在一定范围内,不同卫星反射路径上的等延迟区可进行叠加,以达到增强反射信号的目的,有利于反射信号的探测和利用。同时,交叠的区域内等延迟区的划分更加精细,有利于遥感应用中反射面特征的提取。但是超过一定范围后,等延迟区的交叠变得复杂,不同卫星的反射信号甚至会相互形成干扰,不能随意叠加。
2 GNSS反射信号等多普勒区
通常情况下,接收机、发射机和散射点三者之间存在相对运动,导致接收机接收到的从不同散射点散射来的信号具有不同的多普勒频率。多普勒频移的作用主要有两个,一是进行多普勒频移补偿,可提高采样信号信噪比;二是进行空间滤波,将观测区域划分为更小的观测单元,提高采样信号空间分辨率。
以镜面反射点为参考点,由该点反射信号得到的多普勒频率f0=fD(0)为参考频率。参考图1可得各散射点与参考点的多普勒频差为
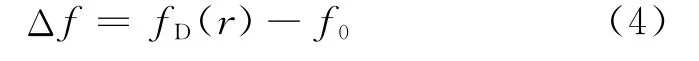
式中:

其中,m,n分别表示发射机到散射点s,散射点到接收机的单位矢量,q为散射向量。
fD(r,t0)为 总 的 多 普 勒 频 移,fD0(r,t0)和fs(r,t0)分别为由发射机和接收机相对运动以及由散射点相对运动引起的多普勒频移。vt,vr分别为接收机和发射机的速度矢量,vs为散射点速度矢量。一般情况下,fs(r,t0)很小,可忽略对总多普勒频移的影响。
2.1 不同卫星高度角下的等多普勒区
设接收机高度为5km,取典型接收机速度vr=0.265 2km/s,卫星高度角θ分别取30°、45°、60°和90°,计算结果如图5所示。图中,Δτ=[1,2…20]·τc,过原点的曲线为Δf=0的等多普勒线,Δf<0的曲线由实线表示,Δf≥0的曲线由虚线表示,Δf的取值间隔为500Hz.

图5 不同卫星高度角下的等多普勒线
通过对比可以发现,等多普勒线的形状随卫星高度角的变化而变化,且随卫星高度角的增大,等多普勒线向原点呈现“收缩”趋势。等延迟环大多集中在[-500,1 000]Hz频带内,等多普勒线对于等延迟线的划分并不均匀。
2.2 不同接收机速度下的等多普勒线
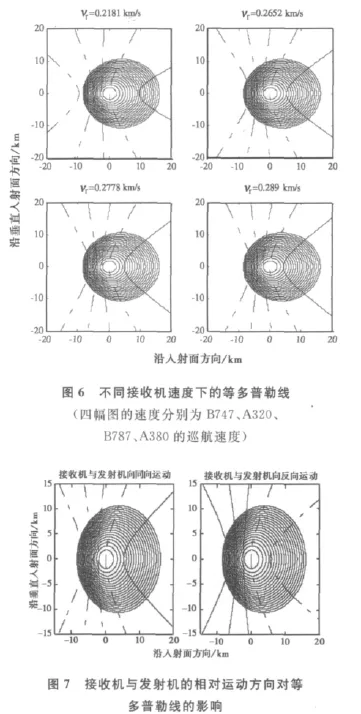
接收机的速度会对等多普勒线造成影响,既包括速度大小,也包括接收机与发射机的相对运动方向。以几种常用型号民航飞机的典型速度值为例进行计算,接收机高度取5km,卫星高度角为60°,结果如图6所示。
随着接收机速度的增加,等延迟线的形状和大小未发生变化,而等多普勒线呈现向镜面反射点“收缩”的趋势,等多普勒区也随之相应减小,频带[-500,1 000]Hz所覆盖的等延迟区逐渐减小。
接收机与发射机相对运动方向的改变对等多普勒线的影响主要表现在对其频移范围的影响不同。当两者相对运动方向发生变化时,等多普勒线的正负频移发生翻转,如图7所示,同向运动时,所显示的等多普勒线的Δf取值为[-500,1 500]Hz(间隔为500Hz);反向运动时,等多普勒线的Δf取值变化为[-1 500,500]Hz.同时,等多普勒区域范围的大小也受发射机与接收机相对运动方向的变化影响。例如,比较同向运动中Δf=-500Hz的等多普勒曲线(实线)和反向运动中Δf=500Hz的曲线(右边第一条虚线),不难发现,两条曲线虽然形状近似,但数值并不相同,即相对应的等多普勒区的大小也不相同。
2.3 不同接收机高度下的等多普勒线
接收机高度的变化同样导致等多普勒线形状和数值的变化。以卫星高度角60°为例,接收机速度取vr=0.265 2km/s,接收机高度分别为1km、5 km、10km和15km情况下的计算结果如图8所示。随着接收机高度的增加,不仅等延迟环的范围扩大,等多普勒线也逐渐远离镜面反射点向外延伸,等多普勒区范围随之加大,但等延迟环大多仍集中在[-500,1 000]Hz的范围内。

图8 不同接收机高度下的等多普勒线
由上述计算分析可知,接收机速度大小、接收机高度、卫星高度角以及接收机与发射机的相对运动方向都是影响等多普勒线数值大小和形状变化的因素。在机载接收机的高度和速度下,等多普勒线对于散射区域的划分不够精细,不论卫星高度角为多少,所感兴趣的等延迟区的大部分区域均涵盖在Δf=[-500,1 000]Hz的多普勒区域范围内,在海洋风场等遥感应用中,最大等多普勒区域的选取一般不宜超过Δf=[-700,1 000]Hz.超出这一范围后,等多普勒区的作用范围通常会超过所感兴趣的等延迟区。当机载接收平台的积分时间Ti取1ms时,多普勒频移影响较小,在进行反射信号相关功率计算时可以忽略。
然而,当接收机安装在低轨卫星(如600~800 km高度)时,其速度变大,同样取Ti=1ms的条件下等多普勒线将会变得密集,其对等延迟区的划分也会变得更加精细。此时多普勒的空间滤波作用不能被忽略,否则将会带来散射信号功率的损失。图9给出了接收机速度vr=7.8km/s,卫星高度角为60°条件下的等延迟线和等多普勒线。

图9 星载高度下的等延迟线和等多普勒线
多普勒间隔的大小由积分时间决定。随着时延多普勒映射接收机(DDMR)接收机的出现,可得到任意多普勒频移下的时延相关功率曲线。由此,可以通过设置更长的积分时间,得到更高的多普勒分辨率(可达Hz级),更加精细的划分时延多普勒单元,用以更加全面地分析海面散射信号特征。
3 结 论
文章分析了GNSS反射信号几何关系,建立GNSS反射信号的本地坐标系和基本的光学近似反射模型,并由此给出了该模型中各个基本参量的计算方法和相互关系。研究了反射信号的等延迟区域和等多普勒区域,给出了等延迟线、等多普勒线的计算方法,并通过数值分析总结了单颗卫星反射信号几何关系模型中不同参量变化对等延迟区和等多普勒区变化的影响,以及多颗卫星的等延迟区变化情况。数值分析结果可为不同接收条件下的接收机参数设计及反射信号相关功率的计算提供依据。
[1]ZAVOROTNY V U,VORONVICH A G.Scattering of GPS signals from the ocean with wind remote sensing application [J].IEEE Transactions,Geoscience and Remote Sensing,2000,V38(2):951-964.
[2]THOMPSON D R,LINSTROM L A,GASPAROVIC R F,et al.Surface roughness estimation from GPS sea reflections[C]//Geoscience and Remote Sensing Symposium.Toronto,Canada,2002:1278-1280.
[3]THOMPSON D R,ELFOUHAILY T M,GARRISON J L.An improved geometrical optics model for bistatic GPS scattering from the ocean surface [J].IEEE Transactions,Geoscience and Remote Sensing,2005,V43(12):2810-2821.
[4]FUNG A K,ZUFFADA C,HSIEH C Y.Incoherent bistatic scattering from the sea surface at L-band[J].IEEE Transactions, Geoscience Remote Sensing,2001,V39(5):1006-1012.
[5]COATANHAY A,KHENCHAR A.Model of GPS signal from the ocean based on an electromagnetic scattering theory:two scale model(TSM)approach[C]// Geoscience and Remote Sensing Symposium.Seoul,South Korea,25-29July,2005:3200-3203.
[6]HUAI-TZU Y.Stochastic Model for Ocean Surface Reflected GPS Signals and Satellite Remote Sensing Applications[D].West Lafayette:Purdue University,2005.
[7]RODRIGUEZ-ALVAREZ N,CAMPS A,VALLLLOSSERA M,et al.Land geo-physical parameters retrieval using the interference pattern GNSS-R technique[J].IEEE Transactions on Geoscience Remote Sensing,2011,V49(1):71-83.
[8]严颂华,张训械.基于GNSS-R信号的土壤湿度反演研究[J].电波科学学报,2010,25(1):8-13.YAN Songhua,ZHANG Xunxie.Retrieving soil moisture based on GNSS-R signals[J].Chinese Journal of Radio Science,2010,25(1):8-13.(in Chinese)
[9]STOSIUS R,BEYERLE G,SEMMLING M,et al.Tsunami detection from space using gnss reflections results and activities from GFZ [C]//IEEE IGARSS'10.Hawaii,USA,2010:3047-3050.
[10]MARCO B,ALEJANDRO E,NICOLAS F,et al.A simulator prototype of delay-doppler maps for GNSS reflections from bare and vegetated soils[C]//IEEE IGARSS'10.Hawaii,USA,2010:3809-3812.
[11]张东和,肖 佐.GPS信号的多普勒效应分析[J].电波科学学报,2002,17(1):42-45.ZHANG Donghe,XIAO Zuo.Analyses of doppler effect for GPS signal[J].Chinese Journal of Radio Science,2002,17(1):42-45.(in Chinese)
[12]周兆明,符 养,薛震刚,等.利用GNSS-R遥感海面风场研究[C]//中国气象学会2005年年会论文集.北京:中国气象学会出版社,2005.
[13]邵连军,张训械,孙 强,等.GPS信号海面散射特性和初步实验结果[J].电波科学学报,2008,23(4):699-703.SHAO Lianjun,ZHANG Xunxie,SUN Qiang,et al.Property of GPS signal scattered from sea surface and preliminary results[J].Chinese Journal of Radio Science,2008,23(4):699-703.(in Chinese)

