考虑邻近排桩遮拦的围护结构土压力计算方法及应用

汪龙兵

(中铁十二局集团建筑安装工程有限公司，山西太原 030024)

1 研究背景

随着城市建筑密度不断加大，建(构)筑物之间的间距越来越近。拟建场地的基坑开挖往往受到邻近建筑物基础的影响，如地下室墙体、深基坑工程或排桩基础等。苏州火车站综合改造基坑工程由地下三层组成:地下第一层为沪宁城际铁路苏州站出站层，基坑采用放坡结合土钉支护开挖，深约15.7 m;地下第二层为轨道交通2号线的站台层，位于地下第一层坑底，为坑中坑结构，深约20.0 m，采用地下连续墙支护;地下第三层为轨道交通4号线的站台层，与地下第二层呈十字交叉，深约24.0 m，采用地下连续墙支护。如图1所示。

在本工程中，作为地铁车站围护结构的地下连续墙外侧布置了大量的群桩基础，或为站房结构的抗拔桩，或为沪宁城际铁路的桥墩桩，其桩径一般1.25 m，桩间距一般3倍～4倍桩径，桩长一般50 m左右，与地下连续墙的距离最小7 m，如图1所示。在这种情况下，作用在拟建基坑地下连续墙围护结构上的土压力属于有限土体土压力范畴，与经典的朗肯或库仑土压力理论采用的半无限土体的假设条件不符合，因此经典土压力理论不适合类似场地条件的计算分析。

图1 深基坑与周围群桩相对位置局部放大

国内外已有一些学者对有限土体土压力的计算进行了初步研究，并指出采用经典朗肯或库仑土压力理论进行有限土体土压力计算是不合适的。何颐华等［1-2］通过室内模型试验与工程实例，得出双排桩支护中有限土体主动土压力的分布，并提出了一种简化的土压力计算方法;高印立［3-4］采用极限分析法研究了有限范围土体土压力，指出常规的朗肯土压力理论与利用极限分析法求得的有限土压力有一定的差异;王文杰等［5］采用极限分析法求得的有限土体主动土压力小于朗肯理论计算的主动土压力;马平等［6］基于极限平衡理论及平面滑裂面假定，在考虑土黏聚力及有限土体宽度的基础上，推导出有限土体滑裂面剪切破坏角的数学表达式，并建立有限土体主动土压力计算公式。

上述研究中，对建立的有限土体土压力计算模型没有考虑基坑的开挖过程(不同深度的影响)，并且一般只针对拟建基坑邻近地下室墙体或另一深基坑的边界情况［7］，这种情况下，有限土体的另一侧边界是不传递侧向土压力的。对于拟建基坑邻近排桩而形成的有限土体的情况，目前尚未见相关文献报道。而考虑排桩遮拦效应对围护结构受力变形产生的有利影响，优化围护结构设计施工参数，对提高施工效率、节约工程成本具有现实意义。

2 计算模型

对于墙背光滑、坡顶水平，经典朗肯与库仑土压力理论得到的主动土压力计算时的剪切破坏角均为θ=45°+φ/2，剪切破坏角是个定值，与深度无关，如图2(a)所示。但当离基坑侧壁一定距离存在构筑物时，滑动土体的剪切破坏面不能剪穿已有构筑物，如图2(b)，此时朗肯与库仑土压力理论中的剪切破坏面不成立。基于极限平衡理论及平面滑裂面假定，在考虑土黏聚力及有限土体宽度的基础上，可建立土压力计算简图如图3所示。

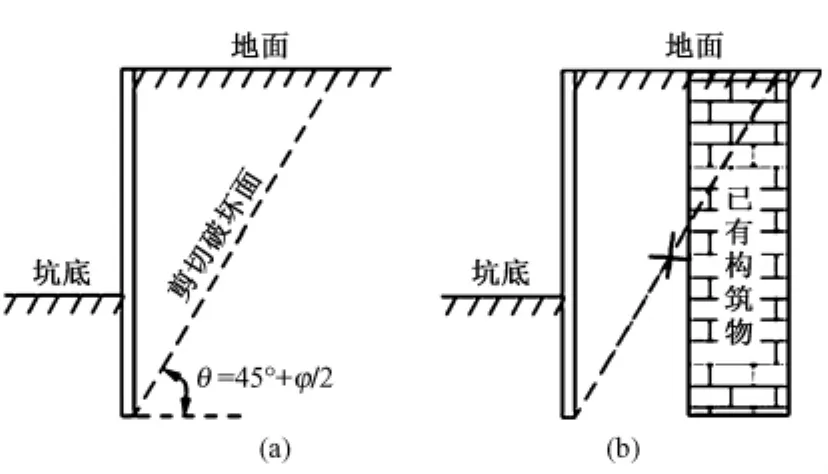
图2 土压力破坏模式分析

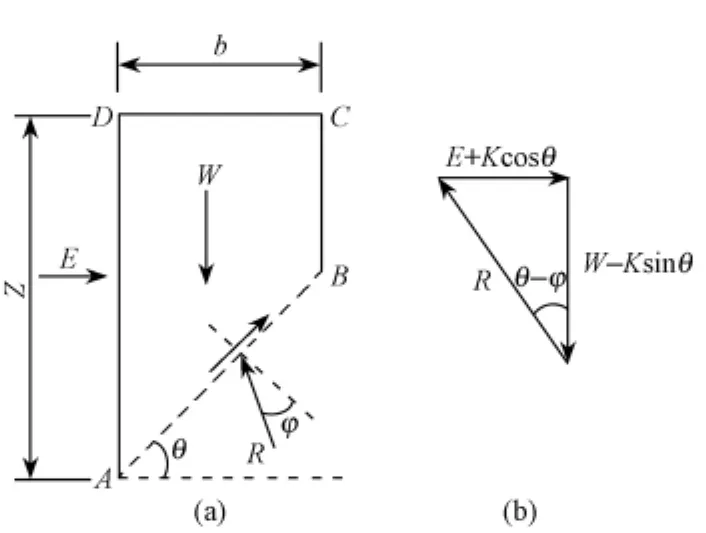
图3 土压力计算示意

若图2(b)中已有构筑物为排桩，则排桩之间的土体还存在一部分绕流土压力作用在排桩与围护结构之间的有限土体上。本文在计算桩土压力分担时，按Tomio塑性理论土压力计算［8］，如图4和图5。

据此，可建立如图6所示的土体受力计算模型。梯形滑动土体ABCD沿墙背DA、滑裂面AB以及有限土体与已有构筑物分界面CB向下滑动，在重力G、连续墙抗力E、下部不动土体反力R、下部土体对上部土体的黏结力C、以及邻近桩基的桩间土体侧压力P作用下，处于极限平衡状态。连续墙抗力E与有限土体作用在支护结构上的土压力大小相等方向相反。

梯形滑动土体ABCD每延米土体重力G可表示为:

图4 土体侧向移动下桩周土被动拱模型

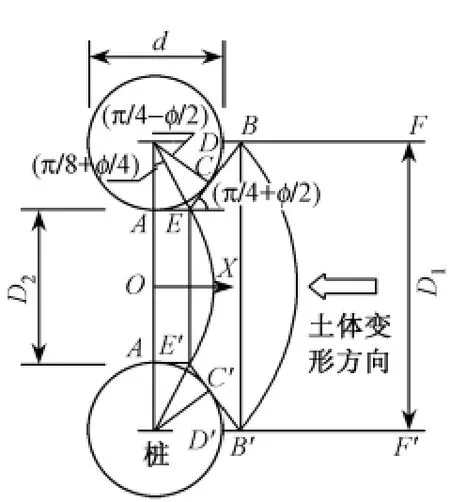
图5 土压力计算示意［8］

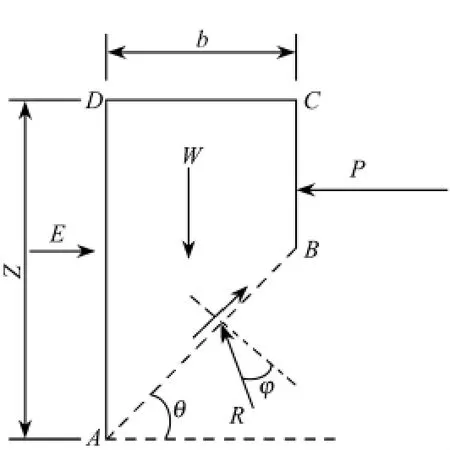
图6 考虑排桩遮拦的有限土体受力分析

式中，γ为土的重度，kN/m3;b为已有构筑物距基坑的距离，即有限土体宽度，m;H为计算点深度，m;θ为滑动破坏面与水平面的夹角，°。

剪切破坏面下部不动土体对上部滑动土体的黏结力C可表示为

根据Tomio塑性理论［9］，桩间土侧向应力σpx为

则桩间土的总侧向压力P可通过σpx沿CB长积分得到。

将已知的G、R、C、P代入，通过建立受力平衡方程，得到

按照极限平衡理论，当dE/dθ=0时，E取极值Ea，即为主动土压力合力，并可求得产生主动土压力Ea时的剪切破坏角θ'值。代入式(4)即可求得当前状态下的极限主动土压力大小。

由于剪切破坏角θ'随深度z变化使主动土压力强度e不再随深度线性分布，很难根据e=dE/dz求得主动土压力强度的表达式。但可以采用差分的形式进行主动土压力强度计算，即

式(5)只适合于滑动破坏土体为梯形的情况，如果计算深度较小，有限土体宽度足够宽，剪切破坏土体为三角形时，仍然需采用经典的土压力理论进行土压力强度计算。

当Z≤Btan(45°+φ/2)时，剪切破坏面未通过桩基，此时破坏模式与经典的主动土压力破坏模式相同。

当Z＞Btan(45°+φ/2)，桩墙后的剪切破坏土体为梯形，此时需要桩基的遮拦效应，先计算剪切破坏角，然后代入式(4)计算总土压力，再依据式(5)进行主动土压力强度计算。

3 土压力计算

苏州轨道交通2号线开挖深度为9 m，与地下连续墙最近的排桩距离取7 m。依据汉森加权平均法，基坑范围内的成层地基土等效为均质土层参数为:γ=19.4 kN/m3、c=21.75 kPa、φ =14.5°。根据 Caspe(1996)和李蓓(2004)等人的研究［10］，地下连续墙外侧土层滑裂面的影响深度计算值为28 m，而在Z≤Btan(45°+φ/2)=9.04 m范围内，仍按经典土压力理论计算压力分布。计算得到2号线地下连续墙的理论土压力大小如图7所示，并与朗肯土压力大小进行比较。

从图7中可以看出，两种计算方法得到的土压力强度曲线存在明显差别，朗肯主动土压力大于有限土体主动土压力，深度越大，差别越大;而且有限土体主动土压力与深度为非线性的关系，有别于朗肯土压力的线性关系。

同样，计算得到4号线地下连续墙的实际土压力大小如图8所示，并与朗肯土压力大小进行比较，得到如图7类似的规律。

图7 轨道交通2号线连续墙土压力分布计算

图8 轨道交通4号线连续墙土压力分布计算

4 工程应用

苏州轨道交通4号线车站基坑剖面设计图如图9，原设计中第三层钢支撑间距3 m，根据施工到负三层钢支撑位置(尚未架设支撑)地下连续墙的变形数据，考虑可对钢支撑的间距进行优化。

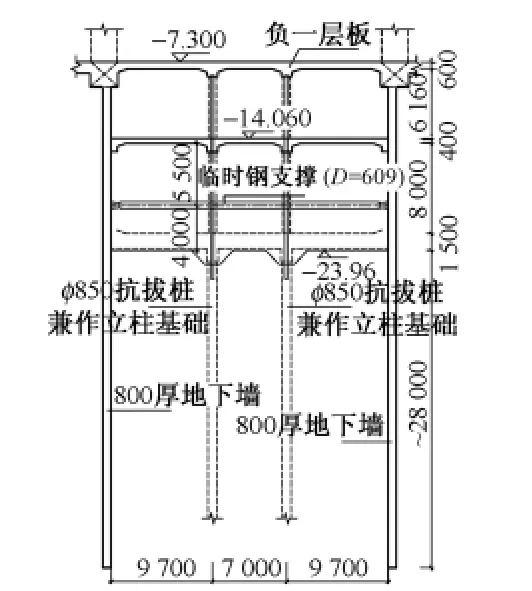
图9 轨道交通4号线设计剖面(单位:mm，高程:m)

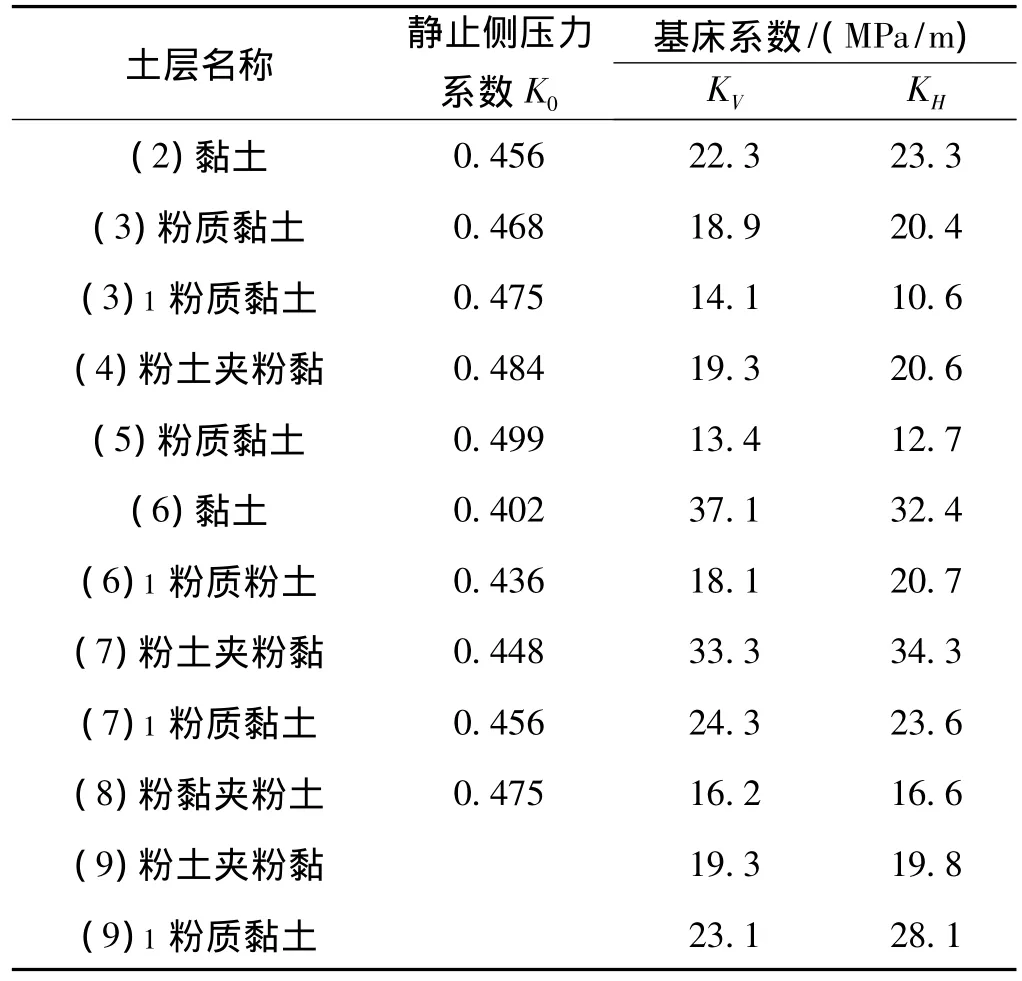
表1 弹性地基梁法地基计算参数

图10 开挖至负三层支撑时连续墙内力分析及与实测和有限元比较

采用平面弹性地基梁方法计算地下连续墙的内力。计算时，主动区分别按经典主动土压力和考虑桩基遮拦的土压力计算，开挖面深度以下按静止土压力取值，静止土压力系数如表1所示;被动区地基土的基床系数同样列于表1，并按m法取值。

图10为开挖至负三层支撑位置时连续墙的内力分析及与整体有限元分析、实测值的比较。

从图10中可以看出，采用朗肯土压力计算的连续墙水平变形最大，且开挖面以下的变形计算值明显高于采用考虑桩基遮拦的修正土压力模型计算得到的结果、整体有限元的计算结果和实际监测结果。开挖面以上连续墙的变形按朗肯土压力和修正土压力计算得到的曲线形状和变形量值比较吻合，这是由于这部分连续墙的土压力没有考虑桩基遮拦的影响，均采用朗肯土压力理论。

由于采用考虑桩基遮拦的修正土压力模型计算得到的连续墙水平变形与实测值最为接近，说明本文建立的考虑桩基遮拦的修正土压力模型是合理的。采用修正土压力计算得到的连续墙变形较实测值有些偏大，这是由于修正土压力模型仍为极限状态值，且没有考虑群桩遮拦效应，这对工程来说是偏于安全的。

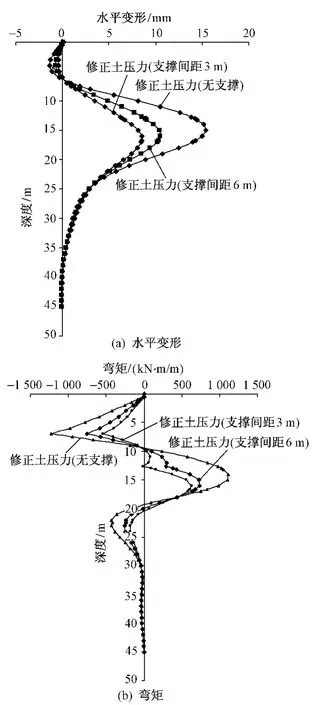
图11 不同支撑间距对连续墙变形和内力的影响

由于在该施工步之后即将施加钢支撑，图11按照修正土压力模型对不同钢支撑间距条件下连续墙的内力与变形进行计算。图中曲线表明，钢支撑间距越大，连续墙的变形和弯矩值越大。修正土压力模式下，钢支撑的间距从3 m增加到6 m，以及不设钢支撑情况下，连续墙的最大水平变形从8.5 mm增加到10.5 mm和15.4 mm;最大负弯矩从540 kN·m/m增加到752 kN·m/m和1 225 kN·m/m;最大正弯矩从628 kN·m/m增加到740 kN·m/m和1 114 kN·m/m。若钢支撑间距按设计值的3 m调整为6 m，可以满足连续墙正截面抗弯极限承载力1 445 kN·m/m(开挖侧)、722.5 kN·m/m(迎土侧)和最大水平位移0.14%H(H为18 m)的要求。

图12 支撑优化的施工效果检验

为检验理论分析结果，图12针对施工参数优化情况下，采用整体有限元分析，并与两种土压力模式下连续墙的变形和内力计算结果、地下连续墙深层水平变形实际监测数据进行了比较。结果进一步表明，修正土压力模型和整体有限元分析的变形水平与实测最为接近，说明采用修正土压力计算得到的连续墙结构内力是较合理的。实际施工中，采用钢支撑间距6 m进行施工，变形控制在允许范围内，又留有一定的安全储备。

5 结论

本文基于极限平衡理论及平面滑裂面假定，在考虑土体黏聚力及有限土体宽度基础上，结合考虑土拱效应的桩土压力塑性理论计算模型，推导了邻近桩基遮拦下围护结构有限土体主动土压力计算公式。该公式与经典土压力理论相比，能更好地预测本项目基坑开挖过程中围护结构的力学响应，科学指导施工并对施工参数实时优化。

［1］何颐华，杨斌，金宝森，等．双排护坡桩试验与计算的研究［J］．建筑结构学报，1996，17(2):58-66．

［2］于怀昌，李亚丽，陈岗宇．双排悬臂桩在软土地区深基坑支护中的应用［J］．铁道建筑，2007(2):71-72．

［3］高印立．有限土体土压力的计算探讨［J］．建筑科学，2000，16(5):53-56．

［4］高印立．极限分析法计算有限范围土体土压力［J］．建筑结构，2001，31(8):66-68．

［5］王文杰，曾进群，陈小丹．深基坑开挖中有限土体土压力计算方法探讨［J］．岩土工程界，2004，8(3):30-31．

［6］马平，秦四清，钱海涛．有限土体主动土压力计算［J］．岩石力学与工程学报，2008，27(增1):3070-3074．

［7］金亚兵，刘吉波．相邻基坑土条土压力计算方法探讨［J］．岩土力学，2009，30(12):3759-3765．

［8］钱家欢，殷宗泽．土工原理与计算［M］．北京:中国水利水电出版社，1996．

［9］ITO T，MATSUI T．Methods to estimate lateral force acting on stabilizing piles［J］．Soils and Foundations，1975，15(4):43-59．

［10］李蓓，赵锡宏．一种考虑挡土墙变形的深基坑非线性土压力方法［J］．岩土力学，2004，25(11):453-458．