生产商－销售商联合生产库存问题的一般数学模型

熊 浩，孙有望

（1.同济大学交通运输工程学院，上海201804；2.长沙理工大学交通运输工程学院，湖南 长沙410076）

对于生产商－销售商联合生产库存问题，Goyal早在1977就开始研究了，并提出了联合批量（JELS）模型.1986年，Banerjee又提出了批对批（lot－for－lot）的联合经济批量JELS供货模型，Goyal对该模型进行了改进，提出供货周期“n次等量订货”的策略［1］.但是，这些策略都假设生产商先生产，生产期间不发货，完成生产之后才开始供货.后来，Lu将问题的假设由“先生产后供货”变成了更接近现实的“边生产边供货”［2］.但是，其提出的策略仍然假设“销售商等量订货”，而该假设也会使最优策略丢失.因此，Goyal对“等量订货”进行了改进，提出“按比例P／D多次递增”的订货策略［3］.接着，Hill在Goyal的基础上又进行了改进，认为“等比例策略”的合理比例应该在1到P／D之间［4－5］.然后，Goyal在Hill的基础上，又提出“第一次小批量，后面的等批量”策略［6］，最后还提出“等比例修正”策略［7］.

后来，学者王圣东［8］和周永务［9］都对上述一系列的联合批量模型的“改进策略”也提出了质疑，并指出已有策略有明显局限性，只适合少数极端条件.但是，学者王圣东给出的数学模型仍然有一些需要放宽的假设条件，比如：“生产商的库存费率低于销售商”；“在一个生产周期内销售商销售最后一次供货量所需的时间不大于下一个生产周期中生产商生产第一次供货量所需要的时间”；“生产商第一次供货后库存变为零”.另外，文献［10］虽然推导出了更具一般性的“三阶段”订货策略，但是也没有给出一般数学模型.

本文进一步放松了学者王圣东在研究单生产商多销售商问题时提出的随机订货策略数学模型的假设条件，通过分析生产商－销售商联合生产库存系统的库存几何特征，利用最优订货策略的几何特征建立数学模型.从而使该数学模型具有更加宽泛的应用条件，该模型的智能启发式算法能够进行全域搜索，通过实例验证，也具有较好的实用性.

1 销售商与生产商的库存状态分析

1.1 问题的描述

已知生产商的生产率为P；预测到销售商的需求率为D；A1、A2分别表示生产商的生产调整费用、销售商的订货费；h1、h2分别表示生产商的库存费率、销售商的库存费率；假设系统运行在无限时间水平上且不允许缺货；系统采用周期性的生产—订货策略；且生产—订货周期中只生产一次.要求合理的策略：系统最佳的生产供货周期、周期内销售商订货策略、生产商生产开始时销售商的初始库存量，使其即能满足顾客需求以及一些约束条件，又能使整体库存费用最低.

因为假设系统采用的是周期性策略，且周期内只生产一次.所以一般可以以生产开始的时间到下次生产开始的时间作为一个周期.令生产开始时销售商的初始库存为q0，系统策略的周期为T，则周期内的需求量Q＝DT；生产商的策略周期中有两种状态：生产状态和停产状态，则销售商在生产时间内的订货次数为k，在停产时间内的订货次数为m，则策略周期内总的订货次数为n，n＝m＋k，则周期内的订货策略为（ti，qi）i＝1，…，n；H、HB、HV分别表示系统总平均库存、销售商平均库存、生产商平均库存.

1.2 销售商的库存分析

图1 销售商在一个策略周期的库存情况Fig.1 Inventory of the buyer during a strategy cycle

图中，t1，…，tk＋m表示订货时间点；T1，…，Tk＋m表示订货时间间隔；T0表示从开始生产到第一次订货的间隔期；q0表示初始库存；T表示订货周期.订货量qi产生的库存量为：qi2／2D.由图可知，销售商在策略周期结束时的剩余库存就是下个周期开始时的初始库存，因为策略是周期性的，所以每个策略周期开始时销售商的初始库存都相等.由此，可以推导出销售商在策略周期的初始库存等于其在策略结束时的剩余库存.所以，若假设销售商在第一个周期内的平均库存为HB，则其表达式为

1.3 生产商的库存分析

生产商在策略周期中可能存在两个阶段：生产阶段和停产阶段.所以，销售商的订货可能发生在生产商的这两个阶段.

一般情况下，如果在策略周期中，销售商的订货有一些在生产商的生产阶段，有一些发生在停产阶段.此时相邻两次订货的间隔期间生产商可能有三种状态：生产状态、停产状态、生产一段时间再停产，如图2所示.图中，T’表示生产时间；T表示策略周期；t0表示开始生产的时间（t0所对应的竖直虚线段表示销售商有初始库存），也是周期开始的时间；ti表示订货时间点；qi表示订货量；容易理解，图中阴影部分面积表示生产商在策略周期中的库存量.

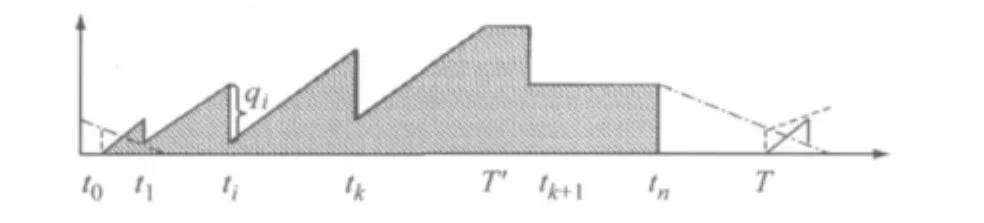
图2 生产商在一个策略周期的库存情况Fig.2 Inventory of producer during a strategy cycle

实际上，生产商在一个策略周期的库存状态还有存在一些特殊的情况，即销售商的订货只发生在生产商的生产期间或只发生在停产期间.这两种情况都是图3的特殊形态.

1.4 系统在策略周期内的库存分析

在图2中，连接初始库存虚线段顶点、销售商订货时刻（发货前）生产商剩余库存顶点，则构成一幅可以反映系统整体库存的图形，如图3所示.图中，AE为策略周期开始时销售商的初始库存量；BF、CG等竖线段表示销售商各次的订货量；EB、FC等斜线段表示生产商库存随生产而增加的量，其斜率为生产率P；三角形左边JN表示销售商的库存随时间消耗情况，斜率为需求率－D.JR表示生产停止的时间点；F’为第二次订货时间点；G’为CG的延长线，使FG’与横坐标平行.

图3 系统在一个策略周期的库存情况Fig.3 Inventory of the system during a strategy cycle

1.4.1 系统整体在策略周期中的库存—时间图的几何特征

图3中的系统在策略周期的库存—时间图存在这样的特征：阴影区域的面积和销售商的库存量相等；五边形AEONJ表示了系统整体在策略周期的库存量；AJ的斜率为（P－D），JN的斜率为－D.

在生态城市建设中，首要目标是为人们提供良好的生活和旅游环境。相关部门要建设公共环境，有目的地策划各区的旅游景点，让大家能够在休闲时光里充分放松，缓解平时工作和生活带来的工作压力，使大家保持愉悦的心情[1]。

以上特征的证明过程如下：

（1）阴影区域（一系列带阴影的小三角形和一个不规则五边形）表示销售商在策略周期的库存量.

图中，对于销售商的订货BF与CG之间的库存量可以用三角形BFG’来表示，又因为ΔBFG’与BFC的底为BF，高为FG’，所以这两个三角形面积相等.同理可证，大三角形AJN中的带阴影的小三角形能表示同一时间段销售商的库存量.

另外，在生产与停产的交界处：SΔJKW’＝SΔJKW，所以SHIKJ＋SΔJKW’＝SΔHIW，又SΔHIW＝SΔHIM，SHIKJ＋SΔJKW’＝SΔHIM，所以不规则五边形HIKA’J的面积能表示销售商在生产期间最后一次订货消耗期间的库存量.而对于生产商停产期间的订货剩余库存顶点连线比较容易理解其刚好表示销售商的在期间的库存量.因此，图中阴影区域刚好能够表示销售商在策略周期的库存量.又因为阴影区里面所包的空白区域是生产商在策略周期的库存量，所以图中阴影加空白区域是系统整体在策略周期中的库存.

（2）线段AB、BC等生产期间生产商发货前剩余库存顶点的联线在同一条直线上，且斜率为P－D.

假设γAB表示AB的斜率，γBC表示BC的斜率.BF′表示在供货周期开始至第一次订货期间的产量，其等于生产率P乘以生产时间EF′.因为根据库存最小的原则下，销售商一般在库存消耗完时才发出订货（假设前置期为零）.所以，该阶段的生产时间

式中：QAE和QBF′分别代表不同时间的系统总库存量.

同理可以证明：BC的斜率γBC＝P－D，所以AB，BC在一条直线上.同理，A′B′和B′C′的斜率都等于D，所以也在一条直线上.所以，生产商的各个订货时点的库存点的连线正好在三角形AJN的两条边上，且三角形的左边AJ的斜率为P－D，右边JN的斜率为－D.

从实际上理解，如果将生厂商与销售商看作成一个虚拟的整体，则其整体库存就是初始库存的基础上，一边生产、一边消耗的持续库存模型.

1.4.2 生产商在策略周期中的库存量

根据上述分析，整个策略周期内的系统库存量为一个大的矩形AEON和一个三角形ANJ构成的五边形里（AEONJ）的面积，矩形的面积为SXAEON＝q0T；假设生产时间为T′，由于策略周期内生产商的生产量等于需求量之和，即PT′＝DT，所以T′＝的高为所则若假设系统的平均库存为H，其可以表示为从而生产商的库存Hv由系统平均库存减去销售商的平均库存HB，为

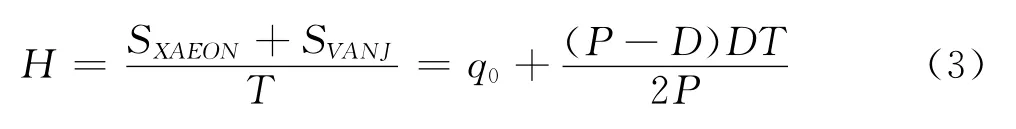
2 数学模型构建及求解

2.1 模型构建

不同的订货策略会使这些库存时间量在生产商和销售商之间进行重新分配（图4中，阴影部分的面积为销售商的库存；剩下的面积是生产商的库存），并且分配还会产生订货费.所以最优订货策略的几何求解可以描述为：在一个大的矩形和一个三角形构成的五边形里（如图中的五边形AEDNJ）中，在JL左边，每画一条竖线段就会生成另一条斜率为P的边与三角形的边AJ构成一个小三角形（如图中的AEB和BFC）或在五边形的中线部分构成一个四边形（如图中的HIKJ）；在JL的右边，就是在重新分配之后能带来的库存费用的节约值与产生的订货费之间进行比较.

图4 生产商在一个策略周期中的库存情况Fig.4 Inventory of the producer during a strategy cycle

因为系统在一个策略周期的平均费用为周期内平均订货费用和平均库存费用之和，所以其表达式为

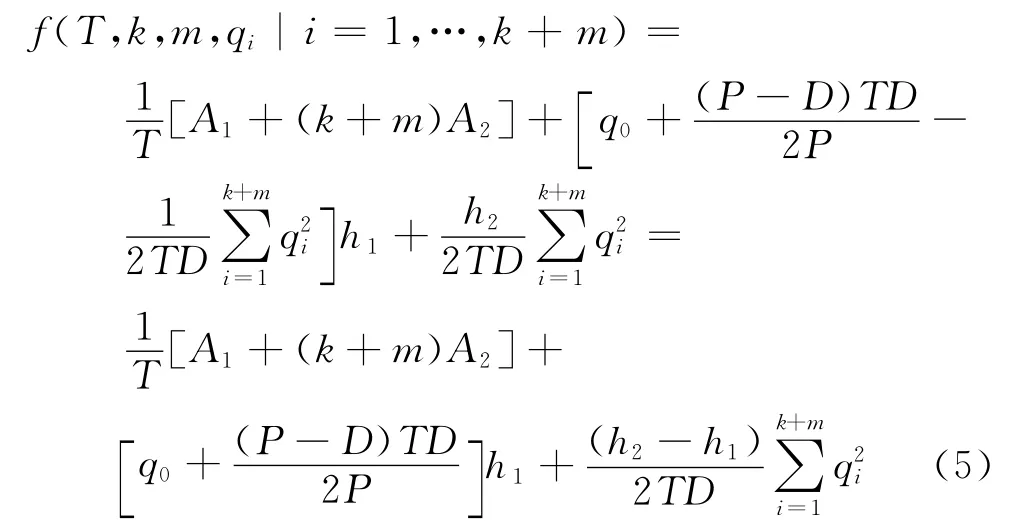
若系统销售商订货发生在生产商生产期间T′内的订货次数为k，则变形得且在生产商的生产阶段内，销售商的当期订货量不可能超过生产商从开始生产到该次订货的订货时间点时所生产的总产量，即：qi≤q0＋（P－D）ti.由此，可以推导出：qi≤q0＋；因为系统策略周期内销售商是按照其面临的需求进行订货，所以订货量之和等于需求量之和，则有综上所述，生产商－销售商联合生产库存系统的一般数学模型为

一般数学表达式中，式（6）是由订货费用、生产调整费用和库存费用构成的目标函数表达式；式（7）表示发生在生产期间的订货量不超过总需求量；式（8）表示发生在生产商生产阶段的订货量不能超过其剩余库存量；式（9）总订货量等于总需求量；式（10）表示所需求解的变量的取值范围.

2.2 模型求解

利用粒子群算法进行求解，一般步骤为：

（1）初始化种群的个体.首先，可以初步判断策略参数的取值范围.比如：根据企业生成实际预测时间跨度大小来确定最大允许的策略周期、利用最小订货间隔期推导最大订货次数等.然后，随机生成正实数T、自然数k和m，然后随机生成正实数qi；i＝1，…，m＋k.由T、k、m和qi（i＝1，…，m＋k）构成粒子的一个位置，用Xj＝（xj1，xj2，…，xj（k＋m＋3））表示.

（2）检验约束条件.根据上述已生成的初始解代入式（7）～（9），检验初始解是否满足数学模型的约束条件.

（3）计算各个粒子不同位置的适应度.将符合约束条件的解代入目标函数式（6）.

（4）进入主要循环.对于每个微粒，将其适应值与所经历过的最好位置Pj（Pj＝ （pj1，pj2，…，pj（k＋m＋3）））的适应值进行比较，若较好，则将其作为当前的最好位置；对每个微粒，将其适应值与全局所经历的最好位置的适应值进行比较，若较好，则将其作为当前的全局最好位置；根据式（11）和式（12）对微粒的速度和位置进行进化，如

式中：下标j表示微粒的第j维；i表示微粒i；t表示第t代；c1、c2为加速常数，通常在0～2间取值；r1～U（0，1），r2～U（0，1）为两个相互独立的随机函数，Vi＝（vi1，vi2，…，vi（k＋m＋3））是设置的微粒i的飞行速度.

（5）计算结束.如未达到结束条件通常为足够好的适应值或达到一个预设最大代数（Gmax），则返回.

3 实例计算

例1：考虑 Goyal的例子：A1＝400，A2＝25，h1＝4，h2＝5，P＝3200，D＝1 000.

利用粒子群启发式算法对生产商供货商一般数学模型求解，得到最优解为T＝0.557 7，q0＝7.39，k＝3、m＝1、q1＝23.6、q2＝75.6、q3＝229.2、q4＝229.3，总成本为1 792.7.该策略前3次订货发生在生产商的生产期间，后1次订货发生在停产期间.与其他策略的比较下表1所示.

例2：考虑 Goyal的例子：A1＝400，A2＝25，h1＝4，h2＝7，P＝3200，D＝1 000.

利用一般数学模型的启发式算法进行求解，得到的最优解为：T＝0.54152、q0＝9.72、k＝3、m＝2、q1＝31.1、q2＝99.5、q3＝136.96、q4＝136.96、q5＝136.96，总成本为1 938.96.该策略前3次订货发生在生产商的生产期间，后2次订货发生在停产期间.与其他策略的比较见表1和表2.

表1 例1中不同策略的结果比较Tab.1 The results of different strategies

表2 例2中不同策略的结果比较Tab.2 The results of different strategies

以上两个实例中，传统的订货策略（包括Goyal、Lu、Hill等提出的策略）得到的解与最优解有较大的差距，而一般数学模型通过启发式算法求解能够找到比传统策略更好的策略.

4 结语

放宽了订货策略的一些假设，直接针对生产商－销售商联合生产库存系统的库存－时间图进行了比较详细的分析.根据库存－时间图得出一个策略周期的销售商的库存量、系统整体库存量以及生产商库存量的表达式；然后，利用这些表达式得到了目标函数的表达式；接着，利用系统整体的库存－时间图分析出订货策略的一些约束条件：发生在生产商生产阶段的订货量不能超过其剩余库存量；总订货量等于总需求量；发生在生产期间的订货量不超过总需求量；从而得到了一般化的生产商－销售商联合生产－库存管理的数学模型.最后，通过两个实例对该模型进行了验证，与其他策略相比，该模型得到的订货策略确实要更加优化.

［1］Goyal S K.A joint economic－lot－size model for purchaser and vendor：a comment［J］.Decision Sciences，1988，19：236.

［2］Lu L.A one－vendor multi－buyer integrated inventory model［J］.European Journal of Operational Research，1995，81：312.

［3］Goyal SK.A one－vendor multi－buyer integrated inventory model：A comment［J］.European Journal of Operational Research，1995，82：209.

［4］Hill R M.The single－vendor single－buyer integrated production－inventory model with a generalized policy［J］.European Journal of Operational Research，1997，97：493.

［5］Hill RM.Another look at the single－vendor single－buyer integrated production－inventory problem ［J］.International Journal of Production Research，2006，44：791.

［6］Goyal S K，Nebebe F.Determination of economic productionshipment policy for a single－vendor－single－buyer system［J］.European Journal of Operational Research，2000，121：175.

［7］Goyal S K.On improving the single－vendor single－buyer integrated production inventory model with a generalized policy［J］.European Journal of Operational Research，2000，125：429.

［8］王圣东，单供货商多销售商联合生产库存模型［J］.系统工程学报，2006，21：92.WANG Shengdong.Production inventory models for a onevendor multi－buyer integrated system［J］.Journal of Systems Engineering，2006，21：92.

［9］ZHOU Yongwu.Optimal production and shipment models for a single－vendor－single－buyer integrated system［J］.European Journal of Operational Research，2007，180：309.

［10］XIONG Hao.A three－phase policy for single－vendor singlebuyer production－inventory systems［C］／／ICLEM，［S.l.］：Logistics for Sustained Economic Development，2010：3755－3762.